Non-uniform Euler-Bernoulli beams´ natural frequencies

Frecuencias propias de vigas Euler-Bernoulli no uniformes

This paper has studied the problem of natural frequencies for Euler-Bernoulli beams having non-uniform cross-section. The numerically-obtained solutions were compared to asymptotic solutions obtained by the Wentzel-Kramers-Brillouin (WKB) method. It was established that WKB formula precision was higher than 3% for high frequencies (≥ 4 mode).

En el presente trabajo se estudia el problema de frecuencias propias de la viga Euler-Bernoulli de sección no uniforme; se comparan las soluciones del problema obtenidas numéricamente con la solución asintótica lograda mediante el método Wentzel-Kramers-Brillouin (WKB). Se establece que la precisión de las fórmulas WKB es mayor del 3% para frecuencias altas (número de modo ≥ 4).

• HTML (es)
• HTML (en)

Hugo Aya B.¹, Ricardo Cano M.², Petr Zhevandrov B.³

¹Físico y M.Sc., en Física-Mathematicas, Universidad Estatal de Kishinev, Moldavia. M.Sc., en Ingeniería Eléctrica, Universidad de los Andes, Colombia. Profesor, Universidad Distrital Franscisco José de Caldas, Colombia. haya@udistrital.edu.co

²Matemático y M.Sc., en Matemáticas, Universidad Nacional de Colombia. Profesor, Universidad de la Sabana, Colombia. ricardo.cano@unisabana.edu.co

³Ph.D., en Ciencias Físico-Matemáticas, Universidad Estatal de Moscú, Rusia. Profesor, Universidad de la Sabana, Colombia. petr.zhevandrov@unisabana.edu.co

---

RESUMEN

Palabras clave: viga Euler-Bernoulli, método WKB.

---

ABSTRACT

Keywords: Euler-Bernoulli beam, WKB method.

---

Recibido: septiembre 9 de 2009. Aceptado: febrero 10 de 2011

---

Introducción

Vibraciones de vigas no uniformes han sido estudiadas desde el siglo XIX (ver, p. ej., Todhunter, 1893, §1302, sobre las investigaciones de Kirchhoff). Estudios relativamente recientes se pueden ver en Abrate (1995) y en Hsu-Lai-Chen (2008), donde se pueden encontrar referencias y un repaso de resultados. En Abrate (1995) se obtienen las frecuencias propias de vigas Euler-Bernoulli (EB) en el caso especial de coeficientes para los cuales las soluciones de la ecuación EB se expresa en términos de funciones elementales.

Para la ecuación de barra no uniforme (problema de Sturm-Liouville) con parámetros como densidad o sección transversal arbitrarios, cuando la ecuación no se integra ni siquiera en funciones especiales, se usa el método Wentzel-Kramers-Brillouin (WKB), también conocido en la literatura como la aproximación de Liouville-Green (Akulenko-Nesterov, 2005; Geist- McLaughlin, 2001), para encontrar la asintótica de las frecuencias altas. Este método consiste en la obtención de series asintóticas en potencias del pequeño parámetro del problema. No encontramos aplicaciones de esta técnica a la ecuación EB, que es del orden 4 (en contraste con la ecuación de vibraciones de barras, que es del segundo orden), a pesar de que el método WKB está desarrollado para ecuaciones del orden n (Fedoryuk, 1993).

En el presente artículo presentamos los resultados de dicha aplicación. Resulta que el método WKB proporciona resultados que coinciden con los resultados numéricos con el error de menos del 3% inclusive para los números de modos igual a 4, y este error sigue disminuyendo para los modos más altos.

Solución asintótica para una viga no uniforme

Las vibraciones transversales de una viga no uniforme en la aproximación Euler-Bernoulli las describen Tijonov-Samarsky (1972):

[1]

donde E es el módulo de elasticidad del material de la viga, ρ es la densidad de la viga, S(x) es la superficie del corte transversal, J(x) es el momento de inercia del corte transversal con respecto a su eje horizontal y y es el desplazamiento transversal. Notemos que la variación de densidad ρ con respecto a x puede ser incluida en el coeficiente S(x). Supondremos en lo que sigue que las funciones S(x) y J(x) son suaves y positivas en 0 ≤ x ≤ l, donde l es la longitud de la viga.

Buscamos los modos naturales de oscilación de la viga en la forma

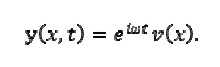
Por lo tanto, al reemplazar en la ecuación (1), resulta:

De esta manera, la ecuación (1) se transforma en la ecuación

[2]

Para condiciones de frontera formuladas en la sección 3 (ver abajo), los autovalores w = w_n de (2) tienden al infinito cuando n → ∞ (Akulenko-Nesterov, 2005); por lo tanto, ε = w^{- 1/2} _n → 0 cuando, n → ∞ y podemos considerar a como un parámetro pequeño de nuestro problema.

Método WKB

Siguiendo la receta tradicional del método WKB, buscamos la solución de la ecuación (2) en la forma

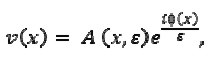[3]

donde:

y las funciones desconocidas Φ(x) y A_j(x), j = 0,1,2,... son suaves.

Sea, w² = 1 / ε⁴ la ecuación en el problema (2) se transforma en la ecuación

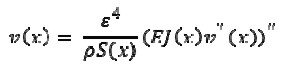
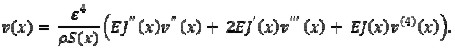[4]

[5]

Luego de algunos cálculos, se obtiene a partir de la ecuaciones (3) y (4) que al separar los términos en el orden de potencias de ε resulta:

[6]

[7]

De los órdenes de potencia , εⁿ, n ≥ 2 , se pueden obtener ecuaciones para A_{n - 1}(x), n ≥ 2, que son de la misma forma que (7) con términos que dependen de A_j, j ≤ n - 2, en la parte derecha.

De la ecuación (6) se obtiene que

[8]

De la ecuación (7) se obtiene

[9]

donde C es una constante arbitraria.

Por lo tanto, reemplazando (8) en (9) se puede expresar la función A₀(x) en la siguiente forma:

[10]

Por lo tanto, la solución v(x) de (2) se puede expresar en la forma:

[11]

Donde

La fórmula (11) representa la combinación lineal de cuatro funciones que aproximan las cuatro soluciones linealmente independientes de la ecuación (2) (Fedoryuk, 1993).

Las soluciones WKB en los casos cuando la solución de (2) se puede obtener en términos de funciones elementales (S, J = constantes, viga uniforme; o S = S₀ (1 + αx)⁴, J = J₀ (1+ αx)⁴ ; en el último caso (Abrate, 1995), la sustitución w(x) = (1 + αx)² v(x) reduce la ecuación a la de una viga uniforme) coinciden con las soluciones exactas; en estos casos las correcciones para las amplitudes A_n. n ≥ 1 se anulan idénticamente.

Ecuación para las frecuencias propias

Para completar el enunciado de nuestro problema, especificamos a continuación las condiciones de frontera para la función v(x) en (2) considerando los casos de una viga empotrada y una viga voladiza.

Viga empotrada en sus dos extremos

Las condiciones de frontera en este caso están dadas por

[12]

Viga no uniforme

Al sustituir la solución (11) en las condiciones de frontera (12) obtenemos un sistema homogéneo de cuatro ecuaciones para los coeficientes Ci, i= 1,2,3,4. Este sistema tendrá soluciones no triviales cuando

[13]

Donde

La ecuación (13) es la ecuación secular para las frecuencias propias w_n = ε^-2

Viga uniforme

Si la viga es uniforme tenemos γ = δ, α = 0 y β = 0 por lo tanto, el determinante en (13) se transforma en

[14]

De lo cual resulta

que coincide con el resultado clásico (Landau-Lifshitz, 1975).

Fórmulas WKB truncadas

Hablando estrictamente, hemos obtenido la asintótica del sistema fundamental de soluciones con la precisión 0(ε) , por lo tanto, tenemos que despreciar los términos de este orden y los órdenes más altos (por ejemplo, e^{- L/ε} = 0(ε^∞)) en (13). Esto simplifica notoriamente los cálculos, de manera que el determinante en (13) se convierte en

[15]

De lo que resulta

y se tiene entonces que

[16]

Este último resultado lo vamos a llamar WKB(t) por truncado. Sin embargo, resulta que (13) proporciona una mejor aproximación a los eigenvalores, lo que vamos a ver en la sección 3.3. La retención de términos 0(ε) en (13) no está rigurosamente justificada, pero su inclusión, primero, no presenta mayor dificultad para la obtención de w_n , y segundo, seguramente no empeora el resultado: las soluciones de (13) poseen la misma propiedad (16) de las soluciones de (15) y en la práctica pueden ser de mayor utilidad. Enfaticemos que las fórmulas truncadas no pasan en las fórmulas exactas cuando el problema admite una solución exacta; en cambio, la fórmula (13) sí pasa en la ecuación secular exacta en los casos cuando esta última se conoce (p.ej., el caso de coeficientes constantes).

Viga voladiza

Las condiciones de frontera para el caso de una viga voladiza⁴ están dadas por

[17]

Viga uniforme

De manera similar al caso anterior, al sustituir la solución (11) en las condiciones de frontera (17) obtenemos un sistema homogéneo de cuatro ecuaciones para los coeficientes Ci, i=1,2,3,4

Este sistema tendrá soluciones no triviales cuando:

[18]

de lo que resulta

Fórmulas WKB(t)

Igual como en la subsección (3.1.3), despreciando los términos del orden O(ε) y los de órdenes más altos en (18), obtenemos:

Este sistema tendrá soluciones no triviales cuando:

[19]

De lo que resulta

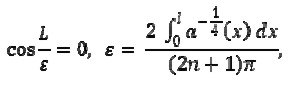
y se tiene entonces el mismo resultado (16).

De manera análoga, se pueden considerar otras condiciones de frontera.

Resultados

A continuación se presentan las frecuencias adimensionales de los seis primeros modos de oscilación para una viga cónica de un metro de longitud, obtenidas mediante el paquete Ansys y las fórmulas WKB y WKB(t). En este caso se tiene para el radio (en milímetros) r (x)= 1 +nx

Con n = 1, 5 , 9, respectivamente (x se mide en metros).

En las primeras tres tablas se muestran los resultados obtenidos para una viga empotrada en sus dos extremos, en la cual el extremo izquierdo tiene un radio de 1 mm y el extremo derecho un radio de 2, 5 y 10 mm, respectivamente.

En las últimas tres tablas se ofrecen los resultados obtenidos para una viga voladiza, en la cual el extremo izquierdo está empotrado y tiene un radio de 2, 5 y 10 mm, respectivamente, y el extremo derecho está libre y tiene un radio de 1 mm.

En todas las tablas que se presentan a continuación, radio 1 significa el radio del extremo izquierdo, y radio 2 el del extremo derecho.

Primer caso (viga empotrada en sus dos extremos)

Como ejemplo, presentamos las gráficas de las eigen funciones del cuarto modo para el caso de la viga empotrada de radio 1 = 1 mm y radio 2= 10 mm, obtenidas mediante el método WKB y el paquete Ansys.

Conclusiones

Los resultados numéricos presentados en la sección 3.3 muestran que la aproximación WKB proporciona valores de las frecuencias propias con precisión mayor del 3% para los modos con números n ≥ 4. Cabe señalar que el método de elementos finitos para altas frecuencias ( n ≥ 10 p. ej.) presenta serios problemas en aplicaciones. Los programas estándares para n ≥ 10 ofrecen inestabilidades computacionales. Se ve claramente que la retención de términos exponencialmente pequeños (fórmulas WKB vs. fórmulas WKB(t)) en la ecuación secular mejora sustancialmente los resultados numéricos. Aunque esta conclusión no es consecuencia de un análisis riguroso, es natural porque las fórmulas WKB (en contraste con WKB(t)) pasan en la ecuación secular exacta para el caso de coeficientes constantes y es el único caso conocido (Abrate,1995) cuando la solución se expresa en términos de funciones elementales.

Agradecimientos

H. Aya expresa su agradecimiento a la Facultad de Ingeniería de la Universidad Distrital por el apoyo económico en el marco del Proyecto Curricular de Ingeniería Electrónica.

R. Cano y P. Zhevandrov expresan sus agradecimientos a la Universidad de La Sabana por el apoyo económico en el marco del proyecto ING-112, y P. Zhevandrov al Conacyt, México, por el apoyo mediante el proyecto 61351.

NOTAS AL PIE

4 Extremo izquierdo empotrado, extremo derecho libre.

---

Referencias

Abrate, S., Vibration of non-uniform rods and beams., Journal of Sound and Vibration, Vol. 185, 1995, pp. 703-716.

Akulenko, L. P., Nesterov, S. V., High-precision Methods in Eingenvalue Problems and Their Applications., Chapman & Hall, 2005.

Fedoryuk, M. V., Asymptotic Analysis., Linear Ordinary Differential Equations, Springer, 1993.

Geist, B., McLaughlin, J. R., Asymptotic formulas for the eigenvalues of the Timoshenko beam., J. Math. Anal. Appl., Vol. 53, 2001, pp. 341-380.

Hsu, J-Ch., Lai, H-Y., Chen, C. K., Free vibration of non-uniform Euler-Bernoulli beams whit general elastically end constraints using Adomian modified decomposition method., Journal of Sound and Vibration, Vol. 318, 2008, pp. 965-981.

Landau, L. D., Lifshitz, E. M., Theory of Elasticity, Course of Theoretical Physics, Vol.7, Pergamon Press, 1975.

Tijonov, A. N., Samarsky, A. A., Ecuaciones de la Física Matemática, Editorial Mir-Moscú., 1972.

Todhunter, I., A History of the Theory of Elasticity and the Strength of Materials., Vol. II, Pt.2, Cambridge. Univ. Press, 1893.

---

Hugo Aya B.¹, Ricardo Cano M.², Petr Zhevandrov B.³

¹ Physicist and M.Sc., in Physical-Mathematics, Kishinev State University, Moldova. M.Sc., in Electric Engineering, Universidad de los Andes, Colombia. Professor, Universidad Distrital Franscisco José de Caldas, Colombia. haya@udistrital.edu.co

² Mathematician and M.Sc., in Mathematics, Universidad Nacional de Colombia.Professor, Universidad de la Sabana, Colombia. ricardo.cano@unisabana.edu.co

³ Ph.D., in Physical-Mathematics Sciences, Moscow State University, Russian. Professor, Universidad de la Sabana, Colombia. petr.zhevandrov@unisabana.edu.co

---

ABSTRACT

Keywords: Euler-Bernoulli beam, WKB method.

---

Received: september 91th 2009. Accepted: febrary 10th 2011

---

Introduction

Non-uniform beams’ viations have been studied since the 19th century (e.g. Todhunter, 1893, §1302 about Kirchhoff’s research). More recent studies can be consulted in (Aate, 1995) and (Hsu-Lai-Chen, 2008) where relevant references and a review of results can be found. Natural Euler-Bernoulli (EB) beam frequencies were obtained in (Aate, 1995) for a special case of coefficients when EB equation solution was expressed in elementary functions.

For the non-uniform rod (Sturm-Liouville problem) equation with variable density or cross-section, when the equation cannot be integrated, even in terms of special functions, one can use the Wentzel-Kramers-Brillouin (WKB) method, also known in the literature as the Liouville-Green approximation (Akulenko- Nesterov, 2005; Geist-McLaughlin, 2001) to find high frequency asymptotics. This method consists of obtaining asymptotic series for solutions in powers of the corresponding small parameter. This technique was applied to the 4th order EB equation (by contrast with the 2nd order rod equation), although the WKB method is developed for nth order equations (Fedoryuk, 1993).

The results of this application are presented in this paper. The WKB method gave results coinciding with numerical results having less than 3% error for mode number 4, and this error became reduced for higher modes.

Asymptotic solution for a non-uniform beam

The transversal viations for a non-uniform beam in a Euler-Bernoulli approach have been described by (Tijonov-Samarsky,1972)

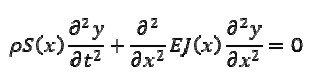[1]

where E was the Young modulus of the beam ρ, was its density, S(x) was the cross-sectional area, J(x) was the moment of cross-section inertia regarding its horizontal axis and y was transversal displacement. Variation of density ρ regarding x could be included in coefficient S(x) It was assumed that functions S(x) and J(x) were smooth and positive for 0 ≤ x ≤ l, where l was the length of the beam.

Natural viation modes for the beam could be expressed as

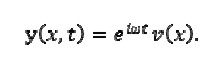
The following was obtained by substituting in equation (1)

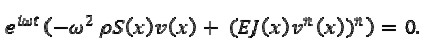
Equation (1) thus became transformed into the following equation

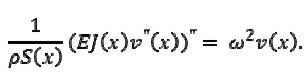[2]

For the boundary conditions formulated in section 3 (see below), eigenvalues w = w_n for (2) tended to infinity as n → ∞(Akulenko-Nesterov, 2005); therefore, ε = w^{- 1/2} _n → 0, as n → ∞ and ^ε could be considered as a small parameter for the problem.

The WKB method

Following the traditional WKB method, the solution of equation (2) could be as follows

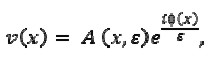[3]

where

and unknown functions Φ(x) and A_j(x), j = 0,1,2,...were smooth.

If w² = 1 / ε⁴ then equation 2 would become transformed to

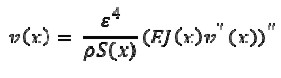
[4]

[5]

After some computation, (3) and (4) would be obtained

Separating terms having equal powers of ε, the following would be obtained

[6]

[7]

From equations for coefficients εⁿ, n ≥ 2 , equations for A_{n - 1}(x) could be obtained, having the same form as (7) with terms depending on A_j, j ≤ n - 2, on the right-hand side.

From equation (6), it followed that

[8]

From equation (7) it followed that

[9]

Where C was an arbitrary constant.

Therefore, substituting (8) in (9), function A₀(x) could be expressed in the following form

[10]

Hence, solution v(x) for (2) could be written as

[11]

Where

Formula (11) would represent a linear combination of four functions approximating the four linearly independent solutions for equation (2) (Fedoryuk, 1993).

In cases when the solution of (2) could be obtained exactly in terms of elementary functions (when S, J were constants, uniform beam; or S = S₀ (1 + αx)⁴, J = J₀ (1+ αx)⁴ ; in the latter case (Aate, 1995), substitution w(x) = (1 + αx)² v(x) would reduce the equation to a uniform beam), WKB solutions coincided with exact solutions; in such cases, corrections to amplitudes A_n. n ≥ 1 removed identically.

Equation for natural frequencies

To complete formulating the problem, boundary conditions for function v(x) in (2) were specified for a clamped beam and a cantilevered beam.

Clamped beam

The boundary conditions in this case were given by

[12]

Non-uniform beam

Substituting solution (11) in boundary conditions (12), a homogeneous system of four equations was obtained for coefficients Ci, i= 1,2,3,4 This system had nontrivial solutions when

[13]

Where

Equation (13) was the secular equation for natural frequencies w_n = ε^-2

Uniform beam

If the beam were uniform, then γ = δ, α = 0 and β; = 0, hence the determinant in (13) would become

[14]

implying that

and this would coincide with the classical result (Landau-Lifshitz, 1975).

Truncated WKB formulas

Strictly speaking, the asymptotics for a fundamental system of solutions having accuracy 0(ε) have been obtained; therefore, terms for this and higher orders must be discarded (for example, e^{- L/ε} = 0(ε^∞)) in (13). This significantly simplifies the calculations. The determinant in (13) would thus become

[15]

implying

and thus

[16]

The latter result has been called WKB(t) for "truncated". Nevertheless, it turned out that (13) gave a better approximation to the eigenvalues, as will be seen in section 3.3. The fact that 0(ε) order terms in (13) were retained was not rigorously justified; however, their inclusion did not present additional difficulties in obtaining w_n surely did not worsen the result. Solutions for (13) had the same property (16) as solutions for (15) and could be more useful in practice. It should be emphasised that truncated formulas do not become exact formulas when a problem requires an exact solution; by contrast, formula (13) did become the exact secular equation in cases when the latter was known (e.g., constant coefficients).

Cantilevered beam

The boundary conditions for a cantilevered beam⁴ were given by

[17]

Uniform beam

Similarly to the previous case, substituting solution (11) in boundary conditions (17), led to obtaining a homogeneous system of four equations for coefficients Ci, i=1,2,3,4 .

This system had nontrivial solutions when

[18]

Implying

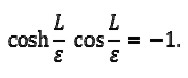
WKB(t) formulas

Just as in subsection 3.1.3, discarding O(ε) terms as well as those of higher orders in (18), led to

[19]

Implying

and obtaining the same result (16):

Other boundary conditions could be considered.

Results

The non-dimensional frequencies for the first six viation modes for a 1 m length conical beam were obtained by using ANSYS simulation package and WKB and WKB(t) formulas. In this case, radius would be (in millimetres r (x)= 1 +nx

with n = 1, 5 , 9 (x in meters).

The first three Tables give the results for a clamped beam, with left end radius being 1 mm and right end 2, 5 and 10 mm.

The last three Tables show the results for a cantilevered beam whose left end was clamped and had 2, 5 and 10 mm radius, the right end being free and 1 mm radius.

Radius 1 means left-end radius and radius 2 the right end in all Tables.

First case (clamped beam):

As an example, graphs are presented for 4^th mode eigenfunctions in the case of a cantilevered beam having 1=1mm radius and 2=10mm radius obtained by the WKB method and the ANSYS package.

Conclusions

The numerical results given in Section 3.3 showed that the WKB approach provided natural frequency values having higher than 3% precision, even for modes having numbers n ≥ 4. It is worth noting that the finite element method for high frequencies (e.g. n ≥ 10 ) led to serious problems in applications. Standard programmes for n ≥ 10 revealed computational instability. It was clearly seen that retaining the exponentially small terms in secular equation (WKB formulas compared to WKB(t) formulas) substantially improved the numerical results. Although this conclusion was not a consequence of rigorous analysis, it seemed natural because WKB formulas (as opposed to WKB(t)) become part of an exact secular equation in the case of constant coefficients and in the only known case (Aate,1995) when the solution can be expressed in terms of elementary functions.

Acknowledgements

H. Aya would like to acknowledge partial financial support from the Universidad Distrital’s Engineering Faculty’s Electronic Engineering Curricular Project

R. Cano and P. Zhevandrov would like to acknowledge partial financial support from the Universidad de La Sabana, project ING-112, and P. Zhevandrov acknowledges the support of CONACYT (México), project 61351.

Foot Note

4 Clamped left end, free right end.

---

References

Abrate, S., Vibration of non-uniform rods and beams., Journal of Sound and Vibration, Vol. 185, 1995, pp. 703-716.

Akulenko, L. P., Nesterov, S. V., High-precision Methods in Eingenvalue Problems and Their Applications., Chapman & Hall, 2005.

Fedoryuk, M. V., Asymptotic Analysis., Linear Ordinary Differential Equations, Springer, 1993.

Geist, B., McLaughlin, J. R., Asymptotic formulas for the eigenvalues of the Timoshenko beam., J. Math. Anal. Appl., Vol. 53, 2001, pp. 341-380.

Hsu, J-Ch., Lai, H-Y., Chen, C. K., Free vibration of non-uniform Euler-Bernoulli beams whit general elastically end constraints using Adomian modified decomposition method., Journal of Sound and Vibration, Vol. 318, 2008, pp. 965-981.

Landau, L. D., Lifshitz, E. M., Theory of Elasticity, Course of Theoretical Physics, Vol.7, Pergamon Press, 1975.

Tijonov, A. N., Samarsky, A. A., Ecuaciones de la Física Matemática, Editorial Mir-Moscú., 1972.

Todhunter, I., A History of the Theory of Elasticity and the Strength of Materials., Vol. II, Pt.2, Cambridge. Univ. Press, 1893.