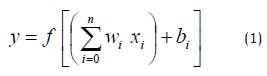
Red neuronal artificial en respuesta a predicciones de parámetros de transferencia de masa (pérdida de humedad y ganancia de sólidos) durante la deshidratación osmótica de frutas
Artificial neural network in response of mass transfer parameters predictions (moisture loss and solid gain) during osmotic dehydration of fruits
Claudia Isabel Ochoa Martinez
Escuela de Ingeniería de alimentos Universidad del Valle, Cali. Colombia. Autora para correspondencia: claudia.ochoa@correounivalle.edu.co
Rec.:03.05.2015 Acep.:24.08.2015
Resumen
Los modelos para predecir las cinéticas de pérdida de agua (ML) y ganancia de sólidos (SG) empleando redes neuronales artificiales (ANN) han demostrado tener mejor comportamiento que los demás modelos desarrollados debido a que correlacionan empíricamente gran cantidad de las variables con ML y SG. La principal ventaja de estos modelos es que son predictivos en vez de correlativos, además pueden implementarse fácilmente en una hoja de datos, y son muy útiles y prácticos para el diseño y control del proceso. El objetivo de este trabajo es emplear un modelo desarrollado con ANN para predecir resultados en procesos de deshidratación osmótica. Se hicieron predicciones de comportamiento con diferentes condiciones de proceso y se validaron con resultados experimentales presentados en la literatura. Se obtuvieron buenas predicciones de ML (MRE 19%) y un comportamiento variable para SG (MRE 62%).
Palabras clave: Aplicaciones agroindustriales, modelo ANN, humedad, secado
Abstract
Models for the prediction of water loss (ML) and solid gain (SG) in osmotic dehydration process based on artificial neural network (ANN) perform better as compared to other models developed for osmotic dehydration, because these models mathematically correlate a wide quantity of processing variables with ML and SG. The main advantage of these models is that they are predictive rather than correlative, also these models can be easily implemented in a spreadsheet, and they are very useful and practical for process design and control. The aim of this work is to use a developed model based on ANN to predict outcomes in osmotic dehydration processes. Predictions were made with different process conditions and were validate by using experimental data reported in literature. Good predictions of ML (MRE 19%) and variable behavior for SG (MRE: 62%) were obtained.
Keywords: Agroindustrial applications, ANN model, drying, fruits, moisture.
Introducción
La deshidratación osmótica (OD), se usa como pre–tratamiento en procesos de secado de frutas tales como secado con aire, microondas o liofilización, para mejorar las propiedades nutricionales, sensoriales y funcionales de las frutas, reducir el daño térmico y minimizar los cambios de color y sabor. El proceso de OD consiste en sumergir la muestra en una solución acuosa concentrada de sacarosa u otros solutos como glucosa, miel o cloruro de sodio y, debido a la diferencia de concentraciones, parte del agua se elimina de la fruta, los solutos de la solución entran al material y se presenta un flujo pequeño de solutos desde la muestra hacia la solución (Sablani et al. 2003). Las principales dificultades para modelar las cinéticas de la OD son la existencia de estos flujos simultáneos y opuestos y la gran cantidad de factores que afectan la velocidad de difusión del agua y los solutos tales como la concentración y la temperatura de la solución osmótica, el tiempo de inmersión, el tamaño y la forma del producto a deshidratar, la relación másica solución: fruta, el nivel y tipo de agitación, la porosidad del material, el tipo de agente osmótico y la presión del proceso (Van Nieuwenhuijzen et al. 2001).
Debido a la complejidad de este proceso, se han hecho muchos esfuerzos para desarrollar modelos para predecir las cinéticas de transferencia de masa en OD. Ochoa–Martínez & Ayala–Aponte (2005), presentan revisiones de los modelos fenomenológicos y empíricos más empleados. Sin embargo, ninguno incluye todas las variables involucradas en el proceso y su uso está limitado a las condiciones en las cuales el modelo se desarrolló por ser procesos correlativos en vez de predictivos. Debido a estas limitaciones, se recomienda el uso de redes neuronales artificiales (ANN) para modelar el proceso y aplicar estos modelos en forma práctica. Sin embargo, muy pocos trabajos se han reportado aplicando esta técnica a la OD.
Se han realizado pruebas en diversos alimentos para modelar y predecir las cinéticas de transferencia de masa durante la OD. El objetivo de este trabajo fue probar la eficiencia de las ANN en la modelación y predicción del comportamiento de un alimento "modelo" sometido a OD. Poligné et al. (2002), y Olmos et al. (2004); emplearon ANN para simular el proceso de deshidratación e impregnación de carne de cerdo. Debido a que la solución deshidratante estaba constituida por una mezcla de sal, glucosa, agua y saborizante, las variables de entrada consideradas fueron la temperatura, la concentración de azúcar y la concentración del saborizante. El objetivo de estos dos trabajos fue el de desarrollar un modelo usando ANN para predecir la pérdida de agua, las ganancias de sal, fenol y azúcar, el pH y la actividad del agua en la OD de carne de cerdo saborizada. Comparando la desviación estándar experimental con la desviación estándar de los valores predichos y evaluando los coeficientes de correlación, se concluyó que el modelo pudo simular el proceso en la mayoría de los casos.
Baruch et al. (2004), desarrollaron un modelo utilizando ANN para predecir la pérdida de agua en OD de cubos de manzanas, papas y batatas simultáneamente. En este trabajo se empleó un modelo de ANN recurrente (diferente al perceptron multicapa). Las variables de entrada fueron la temperatura, la concentración de la solución osmótica y la pérdida de agua de los productos estudiados. Se concluyó que el modelo tuvo buena capacidad de generalización.
Ochoa–Martínez & Ayala–Aponte (2007), desarrollaron un modelo para predecir simultáneamente las cinéticas de transferencia de masa (pérdida de agua y ganancia de sólidos) para deshidratación osmótica de cilindros de manzana en función de seis variables de proceso: temperatura y concentración de la solución osmótica, tiempo de inmersión, área superficial, relación másica solución: fruta y nivel de agitación. Posteriormente, Ochoa–Martínez et al. (2007), desarrollaron un modelo más general para predecir la pérdida de agua (ML) y la ganancia de sólidos (SG) en OD de varias frutas. Este modelo incluye como variables de entrada nueve de los principales factores que afectan la OD: temperatura y concentración de la solución osmótica, tiempo de inmersión, relación másica solución: fruta, nivel de agitación, área superficial y longitud característica de la muestra, y humedad inicial, concentración inicial de sólidos y porosidad del material. Estas tres últimas variables se consideraron para representar el tipo de fruta. Se concluyó que el modelo ajusta los datos en forma confiable y muestra las tendencias típicas en el comportamiento de las variables. Este modelo consiste en un sistema de ecuaciones fácilmente programable en una hoja de cálculo, lo que permite a los usuarios simular el proceso de OD de frutas (manzana, banano, mango, kiwi, papaya y piña) para un amplio rango de condiciones.
Lertworasirikul et al. (2010), modelaron la transferencia de masa en OD para cáscara de lima kaffir. Estos autores relacionaron la concentración de soluto, la temperatura de proceso y el tiempo de inmersión con la pérdida de agua y la ganancia de sólidos. Como en los casos anteriores la modelación con ANN resultó tener mejor generalización que los modelos de regresión múltiple. Prakas Maran et al. (2013), compararon las metodologías de superficie de respuesta y ANN en la predicción de pérdida de agua, pérdida de peso y ganancia de sólidos durante la deshidratación osmótica de papaya. Las variables de entrada fueron la temperatura y la concentración de la solución y la velocidad de agitación.
Otros autores han empleado ANN en DO para predecir parámetros de calidad. Chen et al. (2001), utilizaron ANN para desarrollar un modelo para predecir el tiempo de secado y el color, la textura y la relación de rehidratación, en un proceso combinado de deshidratación osmótica y secado con aire en arándanos. Las variables de entrada que utilizaron fueron la concentración y la temperatura de la solución osmótica y el tiempo de contacto. Zenoozian et al. (2009), relacionaron el contenido de humedad, la deformación y el cambio de color en un proceso de osmo–secado de ahuyama con las variables de entrada del proceso.
El objetivo de este trabajo es predecir la pérdida de agua (ML) y la ganancia de sólidos (SG) en el proceso de OD de frutas (manzana, banano, mango, kiwi, papaya y piña), para diferentes condiciones de proceso empleando el modelo de Ochoa–Martínez et al. (2007). Estos resultados se comparan con datos experimentales obtenidos de la literatura. Bajo la hipótesis de que el modelo permite predecir el comportamiento en un amplio rango de condiciones y de frutas, este trabajo tiene importancia en el contexto de aplicaciones industriales, ahorrando experimentos exploratorios de evaluación de condiciones.
Materiales y métodos
Redes neuronales artificiales
Las redes neuronales artificiales (ANN), son una herramienta potente para modelación de datos. Dentro de sus principales ventajas se incluyen la capacidad de modelación sin tener que hacer suposiciones acerca de la naturaleza de los mecanismos fenomenológicos que describen el proceso, la capacidad de aprender relaciones lineales y no lineales entre las variables desde un conjunto de ejemplos, la capacidad de modelar múltiples salidas simultáneamente y la aplicación del modelo a datos nuevos con precisión razonable.
Las técnicas de ANN se han aplicado frecuentemente en diversas áreas de la ciencia y la tecnología de alimentos. Algunas de estas aplicaciones son: cocción, procesamiento térmico, congelación, secado, extracción, procesos con alta presión, entre otros. Aunque como se presentó en la sección anterior no han sido ampliamente usadas en DO.
Las redes neuronales artificiales (ANN), son algoritmos de optimización que intentan modelar matemáticamente el proceso que aprenden (Sablani et al. 2003), utilizando una función matemática no lineal que transforma un grupo de variables de entrada en un conjunto de salida (Poligné et al. 2002). La red neuronal esta formada por células elementales o neuronas agrupadas en diferentes capas e interconectadas de acuerdo con una arquitectura dada. Cada neurona actúa como un elemento de proceso con conexiones de entrada y salida simple. Cada entrada a la neurona (xi) tiene asignado un "peso" (wi) que es un parámetro interno de la red. El sistema calcula primero la suma de los elementos de entrada ponderados por el peso y luego aplica una función para obtener el valor de salida (y) de acuerdo con la ecuación (1) (Poligné et al. 2002; Baroni et al. 2003).
Donde wi es el "peso", xi es el valor de entrada a la neurona y bi (bias) es el término independiente. La función f a través de la cual se procesa la información es llamada función de activación o de transferencia (Baroni et al. 2003).
La estructura más usada es la red multicapa con alimentación hacia adelante (perceptron multicapa, MLP) que consiste en una capa de entrada, una o varias capas ocultas con una función de activación y una capa de salida (Poligné et al. 2002; Sablani et al. 2003; Rai et al. 2005). La red es no supervisada y se realiza ajuste de los errores hacia atrás.
Los coeficientes wi y bi asociados con la capa oculta se agrupan en las matrices W1 y B1 y en forma similar, los coeficientes asociados con la capa de salida se agrupan en las matrices W2 y B2. Por lo tanto, usando notación matricial, la salida para una red con una capa oculta se representa por la ecuación (2).
Donde Y es la matriz de variables de salida, f1 y f2 son las funciones de activación en la capa oculta y en la capa de salida, respectivamente, y X es la matriz de variables de entrada (Hernández–Pérez et al. 2004).
Modelos
Los modelos desarrollados por Ochoa–Martínez et al. (2007), permiten evaluar la pérdida de agua (ML) y la ganancia de sólidos (SG) para un amplio rango de condiciones (Tabla 1) de temperatura (T, °C), concentración de la solución (C, °Brix), tiempo de inmersión (t, h), humedad inicial de la muestra (H, % w/w), contenido inicial de sólidos de la muestra (S, °Brix), porosidad (E), área superficial (A, cm2), longitud característica (l, cm), relación másica solución : fruta (R) y nivel de agitación (G). Para el nivel de agitación únicamente se consideró un valor de uno (1) para los procesos con agitación y un valor de cero (0) para los procesos sin agitación. En la Tabla 2 se presenta la arquitectura de las redes neuronales a partir de las cuales se obtuvieron los modelos para ML y SG. Todos los detalles de la construcción de los modelos se presentan en Ochoa–Martínez et al. (2007).
Modelo para ML

Modelo para SG
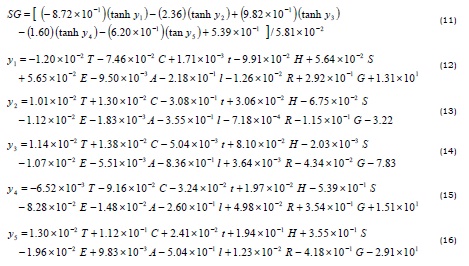
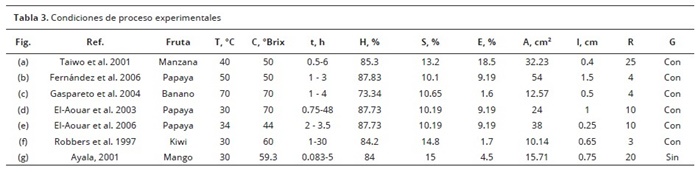
Se emplearon los modelos desarrollados con redes neuronales en Ochoa–Martínez et al. (2007). Se compararon los resultados obtenidos con el modelo para distintas condiciones, con datos extraídos de la literatura (El–Aouar et al. 2003; Gaspareto et al. 2004; El–Aouar et al. 2006; Fernández et al. 2006). En la Tabla 3, se muestran las condiciones de proceso experimentales empleadas por estos autores (otras condiciones de temperatura y concentración se presentan en la Tabla 4).
Resultados y discusión
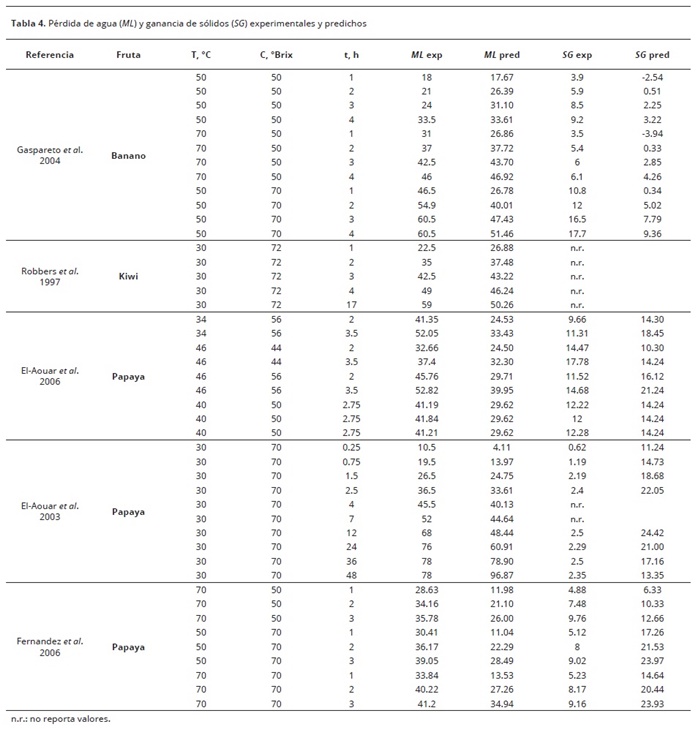
En la Figura 2, se presenta una selección de valores predichos por los modelos frente a los correspondientes valores experimentales de ML y SG. Las condiciones experimentales para estos valores se resumen en la Tabla 3. En la Tabla 4, se exponen los resultados de los restantes conjuntos de datos que no fueron graficados (las condiciones experimentales son las mismas que se presentaron en la Tabla 3, exceptuando la temperatura y la concentración).
En la Tabla 5, se presentan los valores de los errores medios absolutos (MAE) y relativos (MRE) y de las desviaciones estándar de los errores (STDA y STDR). Para el cálculo de los errores para SG se eliminaron los puntos correspondientes a la referencia (El–Aouar et al. 2003), debido a que éstos presentan un comportamiento atípico frente a otros datos experimentales similares.
En términos generales, en la Figura 1 y en la Tabla 4; se puede observar que los modelos predicen relativamente bien el comportamiento de los datos experimentales, aunque la predicción de SG tiene mayor dificultad que la de ML (Tabla 5).
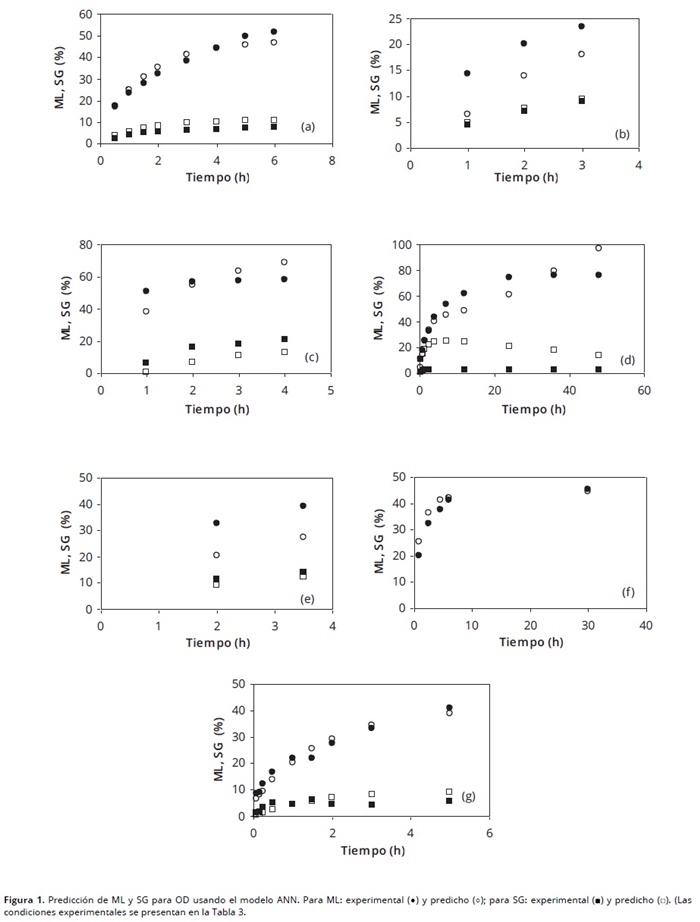
En la Tabla 5, se observa que los errores en la predicción de los datos nuevos estuvieron, en general, aceptables. El error absoluto de ML no se considera alto, si se tiene en cuenta que la pérdida de agua esperada en el proceso de OD es alta (>30%). En cuanto al error absoluto de SG si es alto, teniendo en cuenta que la ganancia de sólidos tiene valores típicos cercanos a 10%. En cuanto al MRE para SG, debe considerarse que debido a la magnitud de SG tan baja, un valor alto de MRE puede ser engañoso, aunque se espera que no pase aproximadamente del 30%.
La predicción de la ganancia de sólidos (SG), es más compleja que la de pérdida de agua (ML). Una de las causas puede ser la falta de estandarización de los métodos experimentales para determinar SG (por ejemplo, algunos autores lavan y secan la muestra justo después de retirarla de la solución osmótica, mientras que otros únicamente la secan). Otra causa, es la alta sensibilidad del valor de SG a condiciones del proceso que no se consideran en los modelos; un ejemplo de esto es la adición de aditivos (ácido láctico y ácido acético) que realizaron El–Aouar et al. (2003), y cuyos resultados se presentan en la Figura 1(d); estos valores de SG tan bajos (>3%) no son típicos para las condiciones experimentales que utilizaron estos autores como se observa en el trabajo de El–Aouar et al. (2006), quienes utilizaron condiciones similares (sin aditivos) y obtuvieron valores de SG cercanos a 14%, lo cual fue bien predicho por el modelo como se observa en la Figura 1(e) y en la Tabla 4.
Conclusiones
Referencias
Baroni. A.F. Menezes. M.R. Adell. E.A.A. Ribeiro. E.P. (2003). Modeling of prato cheese salting: fickian and network approaches. In: J. Welti–chanes, J.F. Vélez–Ruiz and G.V. Barbosa–Cánovas (eds), Transport Phenomena in Food Processing. CRC Press, USA. pp. 192–212.
Baruch. I. Genina–Soto. P. Nenkova. B. Barrera–Cortés. J. (2004). Neural model of osmotic dehydration kinetics of fruits cubes. Lecture notes in artificial intelligence. Lect Notes Comput Sc, 3192, 312–320. doi: 10.1007/978–3–540–30106–6_32.
Chen. C.R. Ramaswami. H.S. Alli. I. (2001). Prediction of quality changes during osmo–convective drying of blueberries using neural network models for process optimization. Dry Technol, 19 (3–4), 507–523. doi: 10.1081/DRT–100103931.
El–Aouar. A.A. Murr. F.E.X. (2003). Estudo e modelagem da cinética de desgratacao osmótica do mamao formosa (Carica papaya L.). Cien Tecnol Aliment, 23 (1), 69–75.
El–Aouar. A.A. Moreira Azubel. P. Lucena Barbosa. J. Murr. F.E.X. (2006). Influence of the osmotic agent on the osmotic dehydration of papaya (Carica papaya L.). J Food Eng, 75(2), 267–274. doi:10.1016/j.jfoodeng.2005.04.016.
Fernándes. F.A.N. Rodrigues. S. Gaspareto. O.C.P. Oliveira. E.L. (2006). Optimization of osmotic dehydration of papaya followed by air–drying. Food Res Int, 39, 492–498. doi:10.1016/j.foodres.2005.10.004.
Gaspareto. O.C.P. Oliveira. E.L. da Silva. P.D.L. Magalhaes. M.M.A. (2004). Influencia del tratamiento osmótico en el secado de la banana "Nanica" (Musa cavendishii L.) en secador de lecho fijo. Inf tecnol, 15 (6), 9–16.
Hernández–Pérez. J.A. García–Alvarado. M.A. Trystram. G. Heyd. B. (2004). Neural networks for the heat and mass transfer prediction during drying of cassava and mango. Innovative Food Science & Emerging Technology, 5(1), 57–64. doi:10.1016/j.ifset.2003.10.004.
Lertworasirikul. S. Saetan. S. (2010). Artificial neural network modeling of mass transfer during osmotic dehydration of kaffir lime peel. J Food Eng, 98(2), 214–223. doi:10.1016/j.jfoodeng.2009.12.030.
Mohebbi. M. Shahidi. F. Fathi. M. Ehtiati. A. Noshad. M. (2011). Prediction of moisture content in pre–osmosed and ultrasounded dried banana using genetic algorithm and neural network. Food Bioprod Process, 89(4), 362–366. doi:10.1016/j.fbp.2010.08.001.
Ochoa–Martínez. C.I. Ayala–Aponte. A.A. (2005). Modelos matemáticos de transferencia de masa en deshidratación osmótica. Cienc Tecnol Aliment, 4 (5), 330–342.
Ochoa–Martínez. C.I. Ayala–Aponte. A.A. (2007). Prediction of mass transfer kinetics during osmotic dehydration of apples using neural networks. Food Sci Technol Res, 40, 638–645. doi:10.1016/j.lwt.2006.03.013.
Ochoa–Martínez. C.I. Ramaswamy. H.S. Ayala–Aponte. A.A. (2007). Artificial neural network modeling of osmotic dehydration mass transfer kinetics of fruits. Dry Technol, 25(1), 85–95. doi: 10.1080/07373930601160882.
Olmos. A. Trelea. I.C. Poligné. I. Collignan. A. Broyart. B. Trystram. G. (2004). Optimal operating conditions calculation for a pork meat dehydration– impregnation– soaking process, Food Sci Technol Res, 37 (7), 763–770.
Poligné. I. Broyart. B. Trystram. G. Collignan. A. (2002). Prediction of mass–transfer kinetics and product quality changes during a dehydration–impregnation–soaking process using artificial neural networks. Application to pork curing. Food Sci Technol Res, 35, 748–756. doi:10.1006/fstl.2002.0939.
Prakash Maran. J. Sivakumar. V. Thirugnanasambandham. K. Sridhar. R. (2013). Artificial neural network and response surface methodology modeling in mass transfer parameters predictions during osmotic dehydration of Carica papaya L. A E J, 52(3), 507–516. doi:10.1016/j.aej.2013.06.007.
Rai. P. Mujumdar. G.C. Dasgupta. S. de S. (2005). Prediction of the viscosity of clarified fruit juice using artificial neural network: a combined effect of concentration and temperature. J Food Eng, 68(4), 527–533. doi:10.1016/j.jfoodeng.2004.07.003.
Sablani. S.S. Rahman. M.S. (2003). Effect of syrup concentration, temperature and sample geometry on equilibrium distribution coefficients during osmotic dehydration of mango. Food Res Int, 36(1), 65–71. doi: 10.1016/S0963–9969(02)00109–6.
Van Nieuwenhuijzen. N.H. Zareifard. M.R. Ramaswamy. H.S. (2001). Osmotic drying kinetics of cylindrical apple slices of different sizes. Dry Technol, 19 (3–4): 525–545. doi: 10.1081/DRT–100103932.
Zenoozian. M.S. Devashastin. S. (2009). Application of wavelet transform coupled with artificial neural network for predicting physicochemical properties of osmotically dehydrated pumpkin. J Food Eng, 90(2), 219–227. doi:10.1016/j.jfoodeng.2008.06.033.