SEGMENTACIÓN SEMIAUTOMÁTICA DEL VOLUMEN DEL HÍGADO EN IMÁGENES DE TOMOGRAFÍA COMPUTARIZADA
Semi-Automatic Liver Volume Segmentation in Computed Tomography Images
GERARDO TIBAMOSO1, Ingeniero Electrónico; ANDREA RUEDA1, M.Sc.; EDUARDO ROMERO1, Ph. D. 1Grupo de Investigación BioIngenium, Universidad Nacional de Colombia, Bogotá, D.C., Colombia. Correspondencia: Carrera 30 # 45-03, Edificio 471. Facultad de Medicina, Centro de Telemedicina, Universidad Nacional de Colombia. Bogotá, D.C., Colombia. edromero@unal.edu.co
Presentado 16 de marzo de 2010, aceptado 4 de junio de 2010, correcciones 28 de junio de 2010.
RESUMEN
El volumen del hígado es un parámetro determinante en cirugía para la extracción de tumores, trasplantes, y en tratamientos de regeneración. Generalmente, la estimación de este volumen se calcula a partir de segmentaciones manuales realizadas por especialistas, siendo éste un proceso tedioso y con poca reproducibilidad de sus resultados. En este trabajo se presenta un método semiautomático para la segmentación del volumen del hígado en imágenes de TAC. El método consiste en superponer manualmente una superficie de triángulos en las imágenes, y deformarla por medio de una ecuación de movimiento asociada a cada uno de sus vértices, para delimitar las fronteras del hígado. La dinámica de la superficie depende de información de intensidades y gradientes, y de relaciones de vecindad entre los vértices, hasta cumplir un número de iteraciones. Comparaciones entre las segmentaciones del método con las segmentaciones de referencia en 20 estudios de TAC, muestran la adaptabilidad de la superficie a la forma y fronteras difusas del hígado, dos de los principales problemas de la segmentación.
Palabras clave: segmentación del hígado, superficies deformables.
ABSTRACT
Liver volume is a significant parameter in surgery for tumor extraction, transplants, and regeneration treatments. Generally, the volume estimation is obtained from manual segmentations performed by specialists, resulting in a tedious process with low reproducibility. In this work a semi-automatic method for the liver volume segmentation in CT images is presented. The method consist in manually superimpose a triangular surface on the images, and use a movement equation associated to each vertex to deform the surface and delimit the liver boundaries. Surface dynamics depend on intensity and gradient information, and neighboring relationships between vertices, until a fixed number of iterations is reached. Comparison between the obtained results and reference segmentations in 20 CT scans, show the surface adaptability to the shape and the diffuse boundaries of the liver, two of the principal segmentation problems.
Key words: Liver segmentation, deformable surfaces.
INTRODUCCIÓN
En la práctica clínica, el volumen del hígado es un parámetro determinante en cirugía para la extracción de tumores, realización de trasplantes, y en tratamientos de regeneración (Frericks et al., 2004; Hermoye et al., 2005; Nakayama et al., 2006). Con frecuencia, la estimación del volumen se consigue sumando las contribuciones de volumen de los vóxeles pertenecientes a las regiones del hígado, delimitadas manualmente por un radiólogo, en un estudio del abdomen realizado por Tomografía Axial Computarizada (TAC) o por Resonancia Magnética (RM) (Heymsfield, 1979).
Con el mejoramiento de la precisión en los equipos de adquisición, pueden obtenerse más de 150 cortes transversales en un estudio de TAC del volumen del hígado, con lo cual la segmentación manual se convierte en un procedimiento tedioso e impreciso debido a la variabilidad inter e intraobservador (algunos estudios reportan hasta un 7,5% (Schroeder et al., 2006; Campadelli et al., 2009)). En consecuencia, se han propuesto en la literatura métodos computacionales para la segmentación del hígado, los cuales pueden clasificarse en técnicas basadas en regiones (Bae et al., 1993, Gao et al., 1996; Nakayama et al., 2006; Rusko et al., 2007; Campadelli et al., 2009), en modelos estadísticos (Lamecker et al., 2004; Heimann et al., 2007; Kainmueller et al., 2007; Okada et al., 2008), y en modelos elásticos (Soler et al., 2001; Hermoye et al., 2005; Dawant et al., 2007; Lee et al., 2007; Wimmer et al., 2007; Garamendi et al., 2007; Fernandez et al., 2009).
Los métodos basados en regiones son altamente automatizados y no requieren etapas de entrenamiento. Una de las mayores dificultades que afrontan estos métodos es la delimitación de fronteras difusas. Estrategias para la construcción de fronteras apoyadas por órganos y tejidos vecinos (como los pulmones o la rejilla costal), intentan darle solución a este problema; sin embargo, apoyarse en estructuras vecinas no siempre es adecuado, debido a la variabilidad que puede presentarse entre pacientes.
Por otro lado, los métodos basados en modelos estadísticos, aprovechan la información a priori de las formas y rangos de intensidades extraídas de un conjunto de hígados, para ser menos sensible ante las fronteras difusas o la presencia de tumores. Esto requiere contar con un amplio conjunto de datos de entrenamiento, donde se consideren las posibles variaciones del hígado; lo cual es un trabajo exigente y no ofrece una completa garantía de afrontar satisfactoriamente todos los casos posibles.
Finalmente, los métodos basados en modelos elásticos pueden relacionar la información de intensidad y gradiente con información a priori de la forma o relaciones de vecindad del hígado. En éstos hay un compromiso entre la inclusión de tumores y la delimitación de fronteras difusas, y generalmente requieren de la intervención del experto para el ajuste inicial o definición de puntos característicos que faciliten la segmentación.
Los resultados de la segmentación del hígado de forma automática son todavía insatisfactorios y se siguen efectuando de manera manual (Heimann et al., 2009). La complejidad del proceso está asociada con las intensidades tan similares entre el hígado y los tejidos vecinos, a la variabilidad de su forma, y a la presencia de lesiones, tumores, y grandes vasos sanguíneos; además, los rangos de intensidad son variables, pues dependen de las características técnicas de las máquinas de adquisición y al uso de sustancias de contraste (Heimann et al., 2009).
En este trabajo se propone un método semiautomático de segmentación del volumen del hígado en imágenes de TAC, basado en modelos elásticos, para la deformación de una superficie discreta, con el cual se afronta la variabilidad de la forma y las fronteras difusas de este órgano. Este documento está organizado como sigue: en la sección 2 se presenta el método propuesto, la experimentación y sus resultados se presentan en la sección 3, y finalmente, en la sección 4 se presenta la discusión y se concluye el artículo.
MÉTODOS
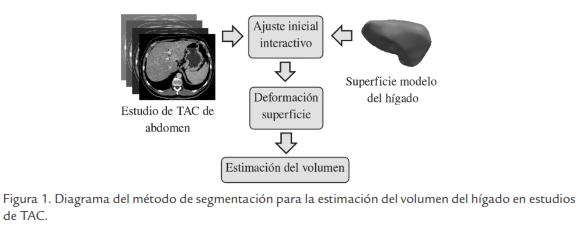
El método propuesto consiste en superponer en las imágenes una superficie modelo del hígado (superficie de triángulos), para luego deformarla iterativamente buscando delimitar las fronteras de este órgano (Fig. 1). La superficie es deformada mediante una ecuación de movimiento asociada a cada uno de sus vértices, que depende de información de intensidades y gradientes, y de relaciones de vecindad entre éstos. El algoritmo se ejecuta hasta cumplir un número dado de iteraciones, suficiente para que los vértices alcancen las fronteras del tejido hepático. Finalmente, el volumen del hígado es estimado sumando las contribuciones de volumen de los vóxeles dentro de la región encerrada por la superficie.

AJUSTE INICIAL
La superficie modelo se ajusta manualmente en las imágenes, a partir de información de intensidad del tejido hepático. Esta superficie se construye a partir de una pila de imágenes binarias que representan la segmentación de un hígado promedio, empleando el método descrito en el diagrama de la Figura 2, basado en (Sullivan y Wu, 2000).

Las imágenes binarias se obtienen combinando un conjunto de segmentaciones de referencia de hígados diferentes con orientaciones espaciales similares, empleando la técnica de label voting (Rohlfing y Maurer, 2005); y suavizando las fronteras de la región resultante por medio de la operación morfológica de cierre (dilatación seguida de erosión). La superficie se construye aplicando inicialmente un algoritmo de marching cubes (Lorensen y Cline, 1987), y refinándola de forma iterativa, con métodos de reducción de triángulos (Schroeder et al., 1992; Hoppe, 1996) y suavizado (Taubin, 1996), preservando su topología1. Finalmente, un método de remallado (Alliez et al., 2002) es aplicado para distribuir de forma homogénea los vértices de la superficie, haciendo aproximadamente constante las distancias entre éstos.
Por otro lado, es necesario extraer información de intensidad del tejido hepático de cada estudio en particular, tanto para el ajuste de la superficie, como para la definición de los parámetros del modelo de deformación. Para esto, se realiza una segmentación manual del tejido hepático en una imagen seleccionada, evitando la inclusión de vasos sanguíneos y tumores, como se presenta en la Fig. 3. Con esto, la distribución de intensidades del tejido hepático se puede aproximar a una distribución normal o Gaussiana, caracterizada por la media µ y la desviación estándar α.

El ajuste inicial de la superficie modelo en las imágenes se realiza de forma manual, dada la variabilidad de la orientación, tamaño y forma del hígado en el abdomen, y a la similitud entre el rango de intensidades de este órgano con las estructuras que lo rodean; características que hacen de un proceso automático una tarea compleja. Para esto, y utilizando la información de intensidad, se extrae de las imágenes una región del hígado y se construye con ésta una superficie, para emplearla como referencia en el ajuste de la superficie modelo en un escenario tridimensional. La construcción de esta superficie se realiza con un método similar al empleado para la construcción de la superficie modelo, aunque menos restringido, dado que se requiere una representación visual de la región del hígado, sin cuidar la topología, los detalles de la forma ni la distribución de los vértices sobre ésta.
DEFORMACIÓN
Luego de superponer la superficie modelo en las imágenes, su deformación iterativa depende de las fuerzas aplicadas en sus vértices (McInerney y Terzopoulos, 1999). Así, la dinámica de cada vértice está gobernada por la siguiente ecuación

donde xit+1 es la posición del i-esimo vértice estimada para el tiempo discreto t+1 (paso siguiente), a partir de su posición actual xit (que por simplicidad será notada en adelante como xi) y de las fuerzas de suavizado (fs,i, asociada a las características geométricas de la superficie), de presión y de bordes (fp,i y fb,i, respectivamente, asociadas a las características de las imágenes); siendo cs, cp y cb constantes de ponderación. La fuerza de suavizado (fs,i) se define como

la cual tiende a aplanar la superficie para preservar su suavidad, empujando cada iesimo vértice hacia el centroide de sus Ni vértices vecinos. La fuerza de presión (fp,i) (Cohen, 1991), por su parte, se define como:

donde ni es el vector normal de la superficie asociado a cada vértice, y la magnitud de esta fuerza, que se define inicialmente como:
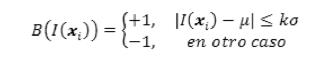
(siendo µ y σ la media y desviación estándar, respectivamente, de la distribución normal de las intensidades del tejido hepático previamente segmentado), generando un componente de movimiento en cada vértice, para acercarlos a las fronteras del hígado. Por último, la fuerza de bordes (fb,i) basada en (Caselles et al., 1997), se define como:

siendo GI(xi) la magnitud del gradiente de las imágenes en xi, obtenida por medio de operadores de Sobel con máscaras de 3x3x3 (Sobel, 1995), y medianR(GI) el valor de la mediana de la distribución de la magnitud del gradiente en la región del tejido hepático previamente segmentado. La fuerza de bordes actúa sobre los vértices en dirección normal de la superficie (ni), llevándolos a los máximos locales del gradiente, haciendo que se fijen en los bordes de los objetos en las imágenes. La función q realza bordes fuertes y reduce bordes débiles, de acuerdo con la información de gradiente de la región previamente segmentada.
Durante la deformación, se aplican conjuntamente operaciones de remallado (Lachaud y Montanvert, 1999) y suavizado (Taubin et al., 1996). Con el remallado, se mantienen las distancias entre vértices vecinos dentro de un rango establecido, fusionando vértices cuando la distancia entre éstos es menor que el umbral mínimo, o insertando vértices para dividir a la mitad los bordes cuya longitud sobrepasa el máximo. Por otro lado, el suavizado consiste en la distribución homogénea de los vértices sobre la superficie, por medio de la aplicación de un filtrado pasa bajos (Taubin et al., 1996), con frecuencia de corte igual a 0.1 y 20 iteraciones, el cual no encoge la superficie.
EXPERIMENTACIÓN Y RESULTADOS
DATOS DE REFERENCIA Y REGLAS DE COMPARACIÓN
Un conjunto de 20 estudios de TAC de abdomen con sus respectivas segmentaciones manuales de referencia, disponibles en www.sliver07.org2 (Heimann et al., 2009), fueron empleados principalmente para la experimentación y evaluación del método de segmentación propuesto. Junto con cinco estudios más, facilitados por el Departamento de Imágenes Diagnósticas de la Universidad Nacional de Colombia, fueron seleccionadas las segmentaciones para la construcción de la superficie modelo del hígado. Estas imágenes han sido adquiridas por diferentes escáneres, y usando agentes de contraste intravenosos. La distancia mínima entre vóxeles se encuentra en el rango de 0,5 mm a 0,8 mm en direcciones x y y, y de 0,5 mm a 5 mm en el eje z (imágenes transversales). Los hígados de estos estudios presentan variabilidad de forma y tamaño, y en muchos de ellos hay presencia de tumores. Por otro lado, las segmentaciones de referencia del hígado incluyen el tejido hepático normal, los vasos sanguíneos internos,3 y los tumores y lesiones que presente este órgano.
Los resultados de las segmentaciones se comparan con las respectivas segmentaciones de referencia, empleando el error de solapamiento volumétrico (comparación vóxel a vóxel), las diferencias relativas de volumen, y las distancias simétricas promedio, raíz cuadrática media y máxima entre las superficies (Heimann et al., 2009). Estas medidas son transformadas a un espacio de puntajes común, para obtener un puntaje único de cada ejecución. Para la transformación, se toman como referencia los resultados de las segmentaciones manuales de un observador independiente, de tal manera que, un puntaje resultante igual a 100 significa que la segmentación se ajusta exactamente a la referencia, 0 es considerado como una falla completa, y 75 corresponde a un resultado similar al obtenido por la ejecución humana (Heimann et al.,2009).
AJUSTE DE PARÁMETROS
Los parámetros que determinan el ajuste inicial y la deformación de la superficie se definieron de forma experimental. En este proceso, inicialmente se realizan experimentaciones para la construcción de las superficies modelo y de referencia. Luego, la superficie modelo se superpone manualmente una sola vez en los estudios de TAC seleccionados, y el método de segmentación es evaluado, cualitativa y cuantitativamente, ante la variación de la función y de los coeficientes que ponderan las fuerzas de deformación. En cada experimento, la deformación de la superficie se realiza durante 300 iteraciones.
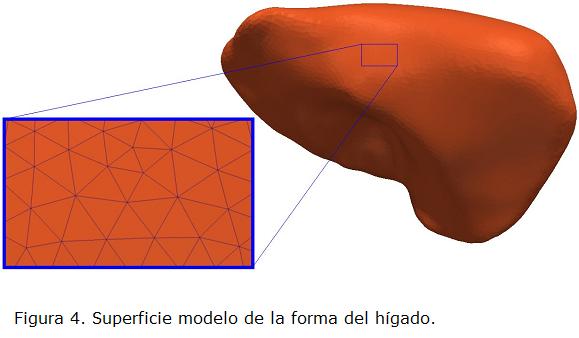
La superficie modelo, ilustrada en la Fig. 4, fue construida combinando las segmentaciones de referencia de 19 hígados. Esta superficie se compone aproximadamente de 600.000 triángulos, que se reducen a 30.000 triángulos (10.500 vértices) luego de la etapa de refinamiento, y con una distancia de 2 mm entre vértices vecinos.
Para la construcción de la superficie de referencia, las imágenes del estudio de TAC (I(x,y,z)) son umbralizadas utilizando la información de intensidad del tejido hepático segmentado (media µ y desviación estándar σ).

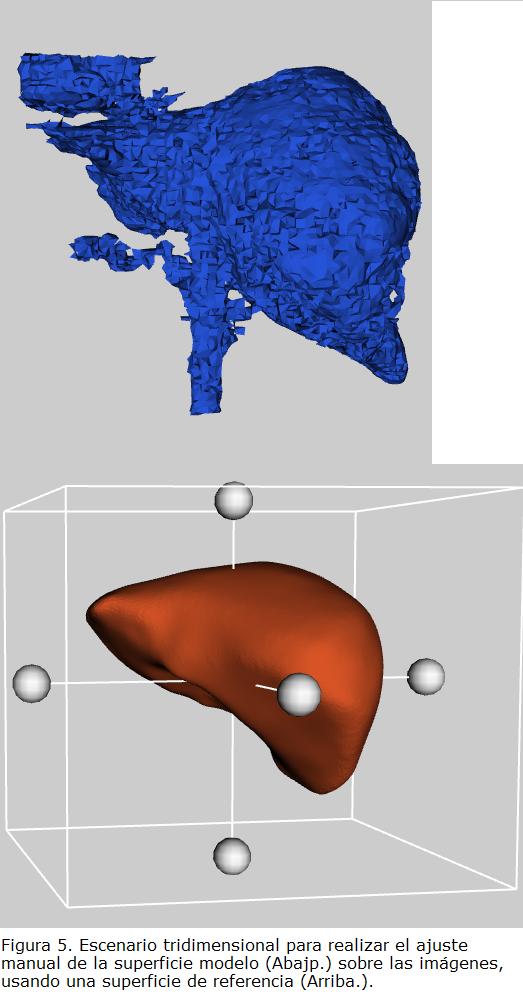
siendo Isal las imágenes resultantes, y k el valor que determina la inclusión o no de vóxeles en la región seleccionada. El valor de k se definió inicialmente igual a 3, para considerar la mayoría de los vóxeles, de acuerdo con la aproximación a una distribución normal. Debido a la inclusión en la superficie de regiones pertenecientes a los grandes vasos sanguíneos, al corazón, al estómago y a la rejilla costal, este valor fue disminuido progresivamente. De acuerdo con los resultados, un valor de igual a 1.5 permite que la superficie represente la región del hígado, sin que tejidos adicionales interfieran significativamente en la superposición de la superficie promedio. En la Fig. 5 se presenta el escenario tridimensional donde aparecen una superficie de referencia y la superficie modelo, y en la Fig. 6 el resultado de la maniobra de la superposición de la superficie en las imágenes. El valor de k igual a 1,5 también es usado para la definición de la función B(I), componente de la fuerza de presión.

Definiciones iniciales para los parámetros B(I), cs, cp y cb, y ligeras modificaciones para algunos de ellos, fueron realizadas para las experimentaciones en dos estudios de TAC seleccionados, donde se evidencia la presencia de fronteras difusas, formas agudas y pronunciadas, pequeñas lesiones, y vasos sanguíneos realzados por sustancias de contraste. El rango de distancias entre vértices vecinos (vértices pertenecientes a un mismo triángulo) se definió entre 2 mm y 5 mm, para representar adecuadamente la mayoría de los detalles de la superficie del hígado, y evitar que éstos se crucen por el efecto de las fuerzas de deformación.
La definición inicial para B(I) consiste en una función cuadrada donde los umbrales µ±1,5σ reducen la inclusión de vóxeles de regiones que comparten rangos de intensidad con el tejido hepático. Posteriormente, con la intención de mejorar la estabilidad del movimiento de los vértices (Ivins y Porrill, 1994), B(I) se define de tal forma que presente una transición continua entre -1 y 1, como una función trapezoidal, donde los puntos de inflexión de esta función se definieron de forma arbitraria, pero considerando que los cruces por cero de ésta y de la función cuadrada (definición inicial), sean los mismos.
El coeficiente cs se define inicialmente igual a 1,0, para generar un componente de desplazamiento que lleve cada vértice hacia el centroide de sus vértices vecinos (restricción fuerte). Posteriormente este coeficiente tomará valores de 0,7 y 0,5, para evaluar la flexibilidad de la superficie con respecto a la delimitación de fronteras difusas. El coeficiente cp se define igual a la mínima distancia entre vóxeles (mdv), para generar un componente de desplazamiento que permita tener información detallada de intensidad, a lo largo de la trayectoria seguida por los vértices. Este coeficiente permanecerá constante durante toda la experimentación. Por último, cb se define inicialmente igual al valor dado a cp, y luego se incrementará en 1,5 veces, para observar el efecto de esta fuerza en el movimiento de los vértices ante la presencia de bordes cercanos en las imágenes.
En los resultados, empleando para B(I) la función trapezoidal, la segmentación del tejido hepático es más selectiva que con la función cuadrada, ya que con esta última se incorporan con mayor frecuencia regiones que no pertenecen al hígado. Dado que la transición de la magnitud de la fuerza de presión generada por la función trapezoidal considera un rango de tolerancia en la estimación de la distribución de intensidades del tejido hepático (que depende de la segmentación manual inicial), ésta resulta ser más apropiada que la función cuadrada para la segmentación, reduciendo errores en la inclusión de tejidos que no pertenecen al hígado.
La inclusión de vasos y lesiones internas y delimitación de fronteras difusas presenta un mejor desempeño cuando cs tiende a 1,0; pero al mismo tiempo, con este incremento se reduce la capacidad de adaptación de la superficie a pequeñas regiones con formas agudas y alargadas. Para garantizar una apropiada delimitación de las fronteras difusas, se define un valor de 0,9 para el parámetro cs, el cual le brinda a la superficie la capacidad de ajustarse un poco mejor a las formas agudas y alargadas. De forma complementaria, se establece el valor de cb en 1,5mdv, permitiendo que la superficie se adapte con mayor precisión a los bordes del hígado.
MÉTODO AJUSTADO
Una vez definidos los valores adecuados para los parámetros en consideración, se procedió a realizar las segmentaciones del hígado en los 20 estudios de TAC disponibles. La superficie modelo del hígado se superpuso manualmente una sola vez en cada uno de los estudios, y el proceso de deformación se aplicó hasta efectuar 300 iteraciones. Algunas segmentaciones resultantes se ilustran en la Fig. 7, mientras que la Tabla 1 presenta los puntajes obtenidos para las segmentaciones de los 20 estudios de TAC.
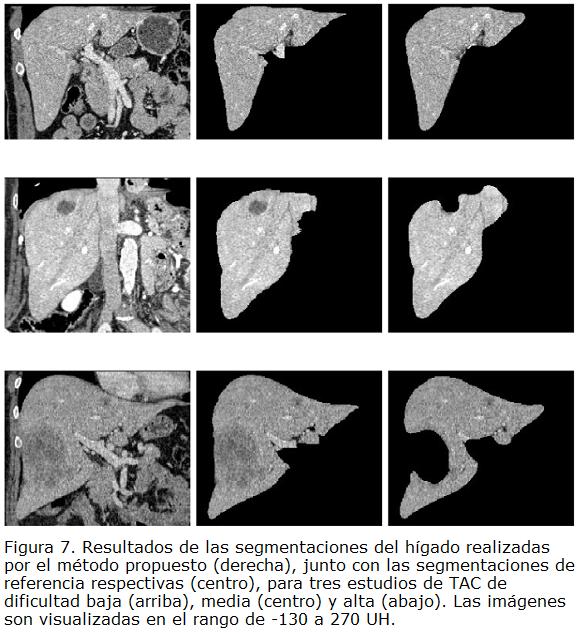

De los resultados, se observó que la superficie, en su proceso de deformación, logra adaptarse a las diversas formas del hígado, delimitando de forma acertada las fronteras difusas de este órgano con los músculos intercostales, el corazón y el estómago.
También se observó que dentro de las dificultades que afronta el método se encuentran el establecer las fronteras entre el hígado y los grandes vasos sanguíneos que entran y salen de éste, la no inclusión de tejido hepático normal cuando hay lesiones o tumores que se interponen y detienen el proceso de la deformación, las variaciones localizadas de intensidad del tejido hepático (por concentración o ausencia de sustancia de contraste) que frenan la superficie, y la no inclusión de pequeñas zonas con formas agudas y alargadas de este órgano. La presencia de tumores y las variaciones localizadas de intensidad, son las razones principales de la obtención de algunos puntajes bajos (hígados anormales). El método también fue probado en 10 estudios adicionales (clasificados como estudios de test en www.sliver07.org), con resultados cualitativos y cuantitativos similares.
DISCUSIÓN
En este artículo se presentó un método semiautomático de segmentación del volumen del hígado, basado en modelos elásticos, el cual emplea información a priori de la forma de este órgano y se adapta a los rangos de intensidad del hígado en las imágenes. Este método afronta adecuadamente la variabilidad de forma y fronteras difusas del hígado, dos de los principales problemas de la segmentación. La formulación discreta, y la capacidad de interactividad que permite acercar la superficie modelo a las fronteras del hígado de interés, son características favorables del método de segmentación, que lo hacen rápido (tiempos de procesamiento entre 5 y 10 min.) y simple para su aplicabilidad en la práctica médica.
El ajuste manual de la superficie es una primera aproximación de la segmentación, lo cual facilita que la superficie alcance las fronteras del hígado rápidamente. Es recomendable ubicar la superficie por fuera de zonas correspondientes al corazón, el estómago, los músculos intercostales, o del riñón derecho, pues dada la similitud de intensidades que se presenta entre estas regiones y el hígado, los resultados pueden no ser adecuados.
El método segmenta el tejido hepático, incluyendo pequeños vasos sanguíneos y algunas lesiones. Dado que pueden presentarse lesiones en diferentes lugares del hígado, que detienen el proceso de la deformación, no todas las zonas del tejido hepático normal son segmentadas adecuadamente. Este problema puede ser resuelto si en una etapa previa se logran segmentar tumores y lesiones, cuyas zonas podrían ser detectadas e incluidas dentro de la segmentación durante el crecimiento de la superficie. Por otro lado, la inclusión de regiones de los grandes vasos se realiza de forma parcial, generando fronteras más cóncavas que las definidas en las segmentaciones manuales. Este problema puede afrontarse en etapas de procesamiento posterior, aprovechando la información del diámetro y rangos de intensidad de estos tejidos.
La superficie funciona como medio de interpolación, con la cual se obtiene una segmentación del hígado compacta y suave. El método maneja la delimitación de fronteras difusas de manera implícita, sin requerir información adicional como la relación con las demás estructuras del abdomen, la cual generalmente es requerida en los métodos basados en regiones. Por otro lado, para afrontar la inclusión de lesiones y grandes vasos sanguíneos, los métodos basados en modelos estadísticos emplean información extraída de datos de entrenamiento. Con el método propuesto, pueden plantearse técnicas de pre y pos-procesamiento para afrontar este problema, lo cual puede ser más eficiente, comparado con el esfuerzo de conseguir y manipular grandes cantidades de datos.
El método propuesto busca segmentar el tejido hepático normal del hígado para la estimación de su volumen, información básica que los especialistas requieren en procedimientos como la extirpación de tumores o trasplantes hepáticos. Información adicional, como la relación entre tejido normal y anormal (tumores) y la distribución de las ramificaciones de los vasos sanguíneos dentro del hígado, no es considerada en el método propuesto, pero son la motivación para desarrollar una herramienta completa que facilite el trabajo del especialista en este campo.
1Mantener la superficie cerrada, sin agujeros, divisiones o auto-intersecciones.
2 MICCAI 2007, workshop on 3D Segmentation in the Clinic: A Grand Challenge. 3 Se considera que un vaso sanguíneo hace parte del hígado, si éste está rodeado completamente de tejido hepático.
AGRADECIMIENTOS
Agradecemos al profesor Alfonso Lozano por la revisión crítica y aporte con imágenes al proyecto, y a los profesores Norberto Malpica y Daniel Rodríguez por la asesoría científica prestada durante el desarrollo del mismo. Este trabajo cuenta con apoyo económico de la Dirección de Investigación de la Sede Bogotá de la Universidad Nacional de Colombia.
BIBLIOGRAFÍA
ALLIEZ P, MEYER M, DESBRUN M. Interactive geometry remeshing. ACM Trans Graph. 2002;21(3):347-354.
BAE KT, GIGER ML, CHEN CT, KAHN CE. Automatic segmentation of liver structure in CT images. Med Phys. 1993;20(1):71-78.
CAMPADELLI P, CASIRAGHI E, ESPOSITO A. Liver segmentation from computed tomography scans: A survey and a new algorithm. Artif Intell Med. 2009;45(2-3):185-196.
CASELLES V, KIMMEL R, SAPIRO G. Geodesic Active Contours. Int J Comput Vis. 1997February;22(1):61-79.
COHEN LD. On active contour models and balloons. CVGIP: Image Underst. 1991March;53(2):211-218.
DAWANT BM, LI R, LENNON B, LI S. Semi-automatic Segmentation of the Liver and its Evaluation on the MICCAI 2007 Grand Challenge Data Set. In: T. Heimann, M. Styner, B. van Ginneken (Eds.): 3D Segmentation in The Clinic: A Grand Challenge; 2007. p. 215-221.
FERNANDEZ-DE MANUEL L, RUBIO JL, LEDESMA-CARBAYO MJ, PASCAU J, TELLADO JM, RAMON E, et al. 3D liver segmentation in preoperative CT images using a levelsets active surface method. Conf Proc IEEE Eng Med Biol Soc; 2009. p. 3625-3628.
FRERICKS BB, CALDARONE FC, NASHAN B, SAVELLANO DH, STAMM G, KIRCHHOFF TD, et al. 3D CT modeling of hepatic vessel architecture and volume calculation in living donated liver transplantation. Eur Radiol. 2004;14:326-333.
GAO L, HEATH DG, KUSZYK BS, FISHMAN EK. Automatic Liver Segmentation Technique for Three-dimensional Visualization of CT Data. Radiology. 1996;201:359-364.
GARAMENDI JF, MALPICA N, MARTEL J, SCHIAVI E. Automatic Segmentation of the Liver in CT Using Level Sets Without Edges. In: IbPRIA 07: Proceedings of the 3rd Iberian conference on Pattern Recognition and Image Analysis, Part I. Berlin, Heidelberg: Springer-Verlag; 2007. p. 161-168.
HEIMANN T, STYNER M, VAN GINNEKEN B. 3D Segmentation in The Clinic: A Grand Challenge. In: T. Heimann, M. Styner, B. van Ginneken (Eds.): 3D Segmentation in The Clinic: A Grand Challenge; 2007. p. 7-15.
HEIMANN T, VAN GINNEKEN B, STYNER M, ARZHAEVA Y, AURICH V, BAUER C, et al. Comparison and Evaluation of Methods for Liver Segmentation from CT datasets. IEEE Trans Med Imaging. 2009;28(8):1251-1265.
HERMOYE L, LAAMARI-AZJAL I, CAO Z, ANNET L, LERUT J, DAWANT BM, et al. Liver Segmentation in Living Liver Transplant Donors: Comparison of Semiautomatic and Manual Methods. Radiology. 2005;234:171-178.
HEYMSFIELD SB, FULENWIDE T, NORDLINGER B, BARLOW R, SONES P, KUTNER M. Accurate Measurement of Liver, Kidney, and Spleen Volume and Mass by Computerized Axial Tomography. Ann Intern Med. 1979;90:185-187.
HOPPE H. Progressive meshes. In: SIGGRAPH 96: Proceedings of the 23rd annual conference on Computer graphics and interactive techniques. New York, NY, USA: ACM; 1996. p. 99-108.
IVINS J, PORRILL J. Statistical snakes: active region models. In: BMVC 94: Proceedings of the conference on British machine vision (vol. 2). Surrey, UK, UK: BMVA Press; 1994. p. 377-386.
KAINMUELLER D, LANGE T, LAMECKER H. Shape Constrained Automatic Segmentation of the Liver based on a Heuristic Intensity Model. In: T. Heimann, M. Styner, B. van Ginneken (Eds.): 3D Segmentation in The Clinic: A Grand Challenge; 2007. p. 109-116.
LACHAUD JO, MONTANVERT A. Deformable meshes with automated topology changes for coarse-to-fine three-dimensional surface extraction. Med Image Anal. 1999 June;3(2):187-207.
LAMECKER H, LANGE T, SEEBASS M. Segmentation of the Liver using a 3D Statistical Shape Model. ZIB; 2004.
LEE J, KIM N, LEE H, SEO JB, WON HJ, SHIN YM, et al. Efficient Liver Segmentation exploiting Level-Set Speed Images with 2.5D Shape Propagation. In: T. Heimann, M. Styner, B. van Ginneken (Eds.): 3D Segmentation in The Clinic: A Grand Challenge; 2007. p. 189-196.
LORENSEN WE, CLINE HE. Marching cubes: A high resolution 3D surface construction algorithm. SIGGRAPH Comput Graph. 1987;21(4):163-169.
MCINERNEY T, TERZOPOULOS D. Topology Adaptive Deformable Surfaces for Medical Image Volume Segmentation. IEEE Trans Med Imaging. 1999;18(10):840-850.
NAKAYAMA Y, LI Q, KATSURAGAWA S, IKEDA R, HIAI Y, AWAI K, et al. Automated Hepatic Volumetry for Living Related Liver Transplantation At Multisection CT. Radiology 2006;240(3):743-748.
OKADA T, SHIMADA R, HORI M, NAKAMOTO M, CHEN YW, NAKAMURA H, et al. Automated Segmentation of the Liver from 3D CT Images Using Probabilistic Atlas and Multilevel Statistical Shape Model. Acad Radiol. 2008 November;15(11):1390-1403.
ROHLFING T, C R MAURER J. Multi-classifier framework for atlas-based image segmentation. Pattern Recognit Lett. 2005;26(13); 2070-2079
RUSKO L, BEKES G, NEMETH G, FIDRICH M. Fully automatic liver segmentation for contrast-enhanced CT images. In: T. Heimann, M. Styner, B. van Ginneken (Eds.): 3D Segmentation in The Clinic: A Grand Challenge; 2007. p. 143-150.
SCHROEDER WJ, ZARGE JA, LORENSEN WE. Decimation of triangle meshes. In: SIGGRAPH 92: Proceedings of the 19th annual conference on Computer graphics and interactive techniques. New York, NY, USA: ACM; 1992. p. 65-70.
SCHROEDER T, RADTKE A, DEBATIN JF, MALAGÓ M, FORSTING M, VALENTIN-GAMAZO C, et al. Variability of Preoperatively Determined Hepatic Volumes in Potential Living Liver Donors. Acad Radiol. 2006;13(2):262-265.
SOBEL I. An Isotropic 3x3x3 Volume Gradient Operator. Hewlett-Packard Laboratories; 1995.
SOLER L, DELINGETTE H, MALANDAIN G, MONTAGNAT J, AYACHE N, KOEHL C, et al. Fully automatic anatomical, pathological, and functional segmentation from CT scans for hepatic surgery. Comput Aided Surg. 2001;6(3):131-142.
SULLIVAN JM, WU Z. 3D Volume Mesh Generation of Human Organs Using Surface Geometries Created from the Visible Human Data Set. In: In Proceedings of the 3rd Visible Human Project Conference, NIH; 2000. p. 5-6.
TAUBIN G, ZHANG T, GOLUB G. Optimal surface smoothing as lter design. Computer Vision, ECCV 96. 1996. p. 283-292.
WIMMER A, SOZA G, HORNEGGER J. Two-stage Semi-automatic Organ Segmentation Framework using Radial Basis Functions and Level Sets. In: T. Heimann, M. Styner, B. van Ginneken (Eds.): 3D Segmentation in The Clinic: A Grand Challenge; 2007. p. 179-188.