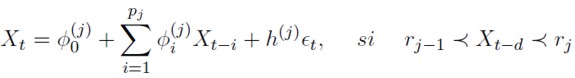
UN MODELO SETAR PARA EL PIB COLOMBIANO
Milena Hoyos*
Johanna Ramos**
Lorena Vivas***
* Magíster en Estadística, se desempeña como profesora e investigadora de la Escuela de Economía de la Universidad Nacional de Colombia. E-mail: nmhoyosg@unal.edu.co. Dirección de correspondencia: Cra 30 No. 45 - 03, Edificio 311, Facultad de Ciencias Económicas, tercer piso (Bogotá, Colombia).
** Estudiante de la Maestría en Ciencias Económicas y se desempeña como contratista de la Dirección de Estudios Económicos del Departamento Nacional de Planeación. Email: ljramosp@unal.edu.co. Dirección de correspondencia: Calle 10a sur No. 3a-16, bloque 3, apto 203 (Bogotá, Colombia).
*** Estudiante de la Maestría en Ciencias Económicas y se desempeña como profesora de la Escuela de Economía de la Universidad Nacional de Colombia. Email: klvivaso@unal.edu.co. Dirección de correspondencia: Calle 26 no. 34a-23 apto 302 (Bogotá, Colombia).
Este artículo fue recibido el 17 de mayo de 2009 y su publicación aprobada el 8 de diciembre de 2009.
Resumen
En este artículo se estudia el comportamiento de la tasa de crecimiento del PIB colombiano entre 1982-2008 a partir de un modelo SETAR (Self-Exciting Threshold Autoregressive), empleando la metodología propuesta por Tsay (1989) y Tong (1990) para la detección de no linealidades relacionadas con la existencia de regímenes cambiantes. Adicionalmente, se comparan los pronósticos generados con los obtenidos en un modelo autorregresivo lineal para diferentes horizontes de predicción, empleando funciones de pérdida simétricas. Los resultados muestran evidencia empírica de que existe no linealidad de umbral en la serie asociada a las altas o bajas tasas de crecimiento registradas por su rezago anual (permaneciendo más tiempo en el régimen de tasas de crecimiento más elevadas) y que el desempeño de los pronósticos del modelo SETAR parece no mejorar con respecto al modelo base.
Palabras clave: ciclo económico, asimetrías, no linealidad, modelos SETAR. JEL: C22, C52, C53, O11.
Abstract
This paper studies the growth rate of Colombian GDP between 1982 and 2008 with a SETAR model (Self-Exciting Threshold Autoregressive), based on the methodology proposed by Tsay (1989) and Tong (1990) for the detection of nonlinearities related to changeable regimens. The main results show empirical evidence of nonlinearity of threshold in the series associated with high or low rates of growth taken in an annual lag, remaining more time in the regime of higher growth rates than in less intensive dynamic regimes. Furthermore, the study compares the performance of the SETAR results with the forecasts generated by a linear autorregresive model in different horizons of prediction, based on a symmetrical loss function. Even though the performance of the forecasts of the SETAR model does not seem to improve with regard to the benchmark model, the results depend on the origin of the forecast.
Key words: business cycle, asymmetries, nonlinearity, SETAR models. JEL: C22, C52, C53, O11.
Résumé
Dans cet article on étudie le comportement du taux de croissance du PIB colombien entre 1982 et 2008 à partir d´un modèle SETAR (Self-Exciting Threshold Autoregressive), en utilisant la méthodologie proposée par Tsay (1989) et Tong (1990) pour la détection de non-linéarités liées à l´existence de régimes changeants. En addition, on compare les prévisions qui s´en dégagent avec cellesobtenues dans un modèle auto-régressive linéaire pour des différents horizons d´analyse, en employant des fonctions de perte symétriques. Les résultats montrent évidence empirique de l´existence de non linéarité de seuil dans la série associée aux hauts ou bas taux de croissance en relation avec leur retard annuelle (en demeurant plus long temps dans le régime de taux de croissance élevés) et que les capacité de prédiction du modèle SETAR n´est pas meilleure que celle du modèle de base.
Mot clés: cycle économique, brèches, non linéarité, modèles SETAR. JEL: C22, C52, C53, O11.
La comprensión de la dinámica de los ciclos económicos ha sido un objetivo de gran interés en el área de la macroeconomía aplicada. Sin embargo, la idea de que las economías funcionan de manera asimétrica durante las fases de expansión y contracción recobró relevancia durante la década de 1980, como consecuencia de las dificultades para dar cuenta de episodios de crisis y del inapropiado uso de métodos lineales en: el análisis de los regímenes del ciclo, la caracterización de sus etapas y la descripción de procesos de cambio estructural.
La existencia de asimetrías y no linealidades en el comportamiento de las variables económicas, independiente de la fuente que las produzca, implica que su estructura probabilística durante la fase de crecimiento no corresponde a la de su fase recesiva. Para Argandoña (1997), las fluctuaciones cíclicas se caracterizan por exhibir longitudes temporales distintas, que suelen ser mayores en el caso de las expansiones, y más volátiles y profundas en las contracciones. Esto hace necesario emplear técnicas que permitan verificar la presencia de no linealidades o comportamientos asimétricos en las series y a partir de ello, modelar y predecir adecuadamente su evolución1.
Con base en estos planteamientos surge un gran número de trabajos dirigidos a modelar y probar la hipótesis de no linealidad de las series cíclicas, dentro de los cuales se destacan los estudios de DeLong y Summers (1986), Hamilton (1989), Diebold y Rudebusch (1990), y Teräsvirta y Anderson (1992). A partir de aproximaciones, estos autores encuentran evidencia de asimetrías en la dinámica del ciclo de negocios. En el caso de Teräsvirta y Anderson (1992), dichas asimetrías están relacionadas con las diferencias en el tiempo entre los puntos máximos y mínimos de los ciclos, siendo las contracciones más cortas e inclinadas que las expansiones.
Así mismo, se han propuesto diferentes métodos estadísticos para modelar no linealidades resultantes de conductas asimétricas a lo largo del ciclo económico. En particular, se ha empleado el modelo SETAR (Self-Exciting Threshold Autoregressive) introducido por Tong (1978), el modelo autorregresivo de cambio markoviano de régimen propuesto por Hamilton (1989), y el modelo autorregresivo de transición suave (STAR) de Teräsvirta y Anderson (1992).
Un gran número de estudios basados en la implementación de las metodologías antes mencionadas, se ha concentrado en la evaluación de las conductas asimétricas del PIB real como principal indicador de la actividad económica, lo que ha contribuido a documentar algunas de sus regularidades, tales como: la mayor profundidad, la volatilidad y la menor persistencia de las contracciones con respecto a las asociadas a las expansiones.
En Colombia, algunos de los trabajos en los cuales se modelan características no lineales de la actividad económica fueron elaborados por Arango y Melo (2001), Misas y Ramírez (2005) y Hoyos (2007). Arango y Melo, y Hoyos estudian el comportamiento no lineal asimétrico de la actividad económica, medida a través del Índice de Producción Industrial (IPR) a partir de modelos STAR y TAR, respectivamente, encontrando evidencia a favor de la hipótesis de no linealidad. Misas y Ramírez modelan el crecimiento económico de largo plazo empleando la metodología de cambio markoviano con dos regímenes, encontrando evidencia de no linealidad en la tasa anual de crecimiento económico y de que la economía colombiana permanece por más tiempo en el régimen de crecimiento sostenido.
En este documento se implementa la metodología SETAR propuesta por Tsay y Tong para probar la hipótesis de no linealidad del ciclo económico del PIB colombiano, y a partir de estos resultados, modelar el comportamiento no lineal de la serie. Dicha metodología ha sido ampliamente utilizada en el análisis de la evolución del PIB, la tasa de cambio, la tasa de desempleo, entre otras series macroeconómicas para las cuales la teoría sugiere características asimétricas y no linealidades.
A pesar de las dificultades aún presentes en los algoritmos propuestos, relacionados con la estimación de los parámetros estructurales, la modelación a través de un modelo SETAR permite reproducir las características no lineales de la serie y en algunos casos, elaborar mejores pronósticos2.
El documento se encuentra dividido en tres secciones. En la primera se describen las metodologías para realizar la prueba de no linealidad, determinar la variable, el valor umbral, el ajuste, la validación y la predicción del modelo. Los resultados empíricos y un análisis comparativo entre los pronósticos obtenidos a partir del modelo lineal base y el SETAR estimado se resumen en el segundo apartado. Por último, se plantean las conclusiones del ejercicio de ajuste del modelo sobre la serie del PIB colombiano.
EL MODELO SETAR
Un proceso estocástico Xt sigue un modelo Self-Exciting Threshold Autoregressive (SETAR) de l regímenes con variable de umbrales Xt−d si satisface la ecuación:
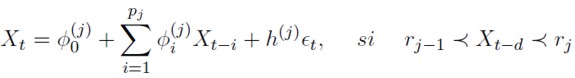 |
[1] |
Siendo j = 1, . . . , l y d un entero positivo, llamado parámetro de retraso. Los umbrales rj (j = 1, . . . , l − 1) son números reales tales que −∞ = r0 < r1 < . . . < rl−1 < rl = ∞. Además, εt es un proceso ruido blanco Gaussiano de media cero y varianza 1. Los coeficientes φ (j) i y h (j) son números reales y los números enteros no negativos p1, . . . , pl denotan los órdenes autorregresivos en cada régimen.
El modelo SETAR, inicialmente propuesto por Tong (1978) es un modelo lineal autorregresivo por tramos, en el espacio de la variable de umbral, capaz de describir ciclos límites asimétricos. A diferencia de los modelos autorregresivos lineales, la estacionariedad de Xt no requiere que todas las raíces del polinomio φ j(B) = 1 − φ (j) 1 B − . . . − φ(j) pj B j estén por fuera del círculo unitario, lo cual significa que a pesar de existir estacionariedad a nivel global, se puede presentar una alternancia entre regímenes explosivos y contractivos. La ecuación muestra además que aun cuando la serie puede ser modelada apropiadamente por un AR lineal, su comportamiento dinámico está determinado por el régimen que ocurre en un momento dado del tiempo.
Se han desarrollado diferentes alternativas para analizar el modelo SETAR. En este trabajo se seguirá la propuesta por Tsay (1989). Esta metodología parte de la identificación del orden p del proceso autorregresivo lineal para el total de datos Xt y la selección del conjunto S de posibles valores del parámetro de retraso d. Esto, con el propósito de llevar a cabo una prueba estadística en la que se contrasta la hipótesis nula de linealidad contra la hipótesis alternativa de no linealidad explicada por la presencia de umbrales, a partir de una regresión ordenada estimada por el método de mínimos cuadrados recurrentes. La estadística de prueba se construye como sigue:
1. Se ordenan los datos de la variable de umbrales X(t−d) por magnitud para luego considerar la regresión ordenada
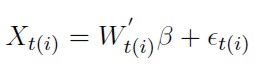 |
[2] |
Siendo W´t (i) = (1, Xt (i)−1,. . .,Xt (i)−p) y t (i) el índice de tiempo de la variable de umbrales ordenada.
2. Luego se estima la regresión anterior por el método de mínimos cuadrados ordinarios para las primeras m observaciones y se obtiene el vector de parámetros estimados, 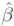 m.
m.
3. Usando el algoritmo de mínimos cuadrados recurrentes, el siguiente paso es calcular los residuos predictivos dados por
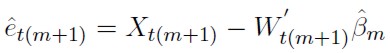 |
[3] |
y los residuos predictivos estandarizados:
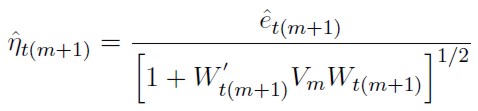 |
[4] |
Siendo 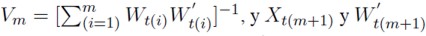 las próximas observación de la variable respuesta y de las regresoras, que son incluidas en la regresión ordenada, respectivamente.
las próximas observación de la variable respuesta y de las regresoras, que son incluidas en la regresión ordenada, respectivamente.
4. A continuación se estima la regresión:
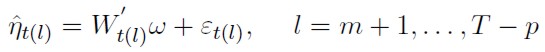 |
[5] |
En la cual m denota el punto inicial de la estimación de mínimos cuadrados recurrentes y T representa el tamaño de la muestra.
5. Finalmente, se prueba la hipótesis HO : ω = 0 contra la alternativa Ha : ω ≠ 0 usando la estadística de prueba:
 |
[6] |
con v = max {1, p + 1 − d}.
Bajo la hipótesis nula de linealidad y un T grande la estadística 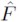 (p,d) sigue aproximadamente una distribución F con p + 1 y T − d − m − p − v grados de libertad.
(p,d) sigue aproximadamente una distribución F con p + 1 y T − d − m − p − v grados de libertad.
Si se detecta no linealidad en la serie, Tsay propone realizar diagramas de dispersión entre los residuales estandarizados o las razones t de las estimaciones recurrentes y la variable de umbrales, con el objeto de determinar el número de regímenes l y los valores de los umbrales r1, . . . , rl−1 asumiendo que, si la serie es no lineal, los residuales (o razones t) deben presentar quiebres en su trayectoria alrededor de dichos valores.
Otro método para identificar los valores umbral de la serie es planteado por Tong (1990), quien propone tomar como candidatos ciertos umbrales y diferentes órdenes autorregresivos en cada régimen para considerar todas las posibles combinaciones ordenadas con ellos, de tal forma que sea posible encontrar la combinación de parámetros que minimicen el criterio NAIC:
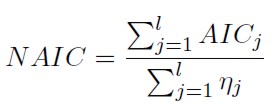 |
[7] |
Donde AICj y ηj denotan el criterio de información Akaike (AIC) y el número de observaciones en el j-ésimo régimen, respectivamente, y l es el número de regímenes.
Una vez se han localizado los umbrales, se procede a ajustar el modelo SETAR, estimando los parámetros de cada régimen por mínimos cuadrados ordinarios y a verificar el cumplimiento de los supuestos3 sobre el conjunto agrupado de los residuales estandarizados.
Aun cuando la metodología SETAR es aplicada especialmente con el propósito de obtener una adecuada descripción del comportamiento dinámico que presenta una determinada variable, a menudo, un objetivo adicional es utilizar el modelo para predecir valores futuros de la serie temporal k pasos adelante. Sin embargo, para k > 1 pasos adelante estos cómputos son más complicados que para el caso lineal. Se han propuesto diferentes procedimientos para este fin, entre los que se cuentan métodos de simulación de Monte Carlo o Bootstrapping, método de errores de pronóstico normal y método de pronósticos ingenuo –ver Granger y Terasvirta (1993).
El pronóstico un paso adelante corresponde a:
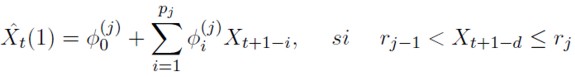 |
[8] |
Los pronósticos k pasos adelante, con k > 1, generados por Monte Carlo son computados tomando el promedio de las N repeticiones:
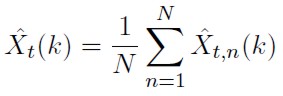 |
[9] |
con
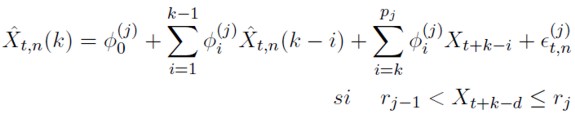 |
[10] |
Expresión en la cual los términos ε(j) t,n, n = 1, . . . ,N, son muestras obtenidas de la distribución de los errores que corresponde, en el caso del modelo SETAR, a una normal con media cero y desviación estándar h j .
RESULTADOS EMPÍRICOS
La serie ajustada a partir del modelo SETAR corresponde a la primera diferencia de la transformación logarítmica del PIB trimestral a precios constantes del año 20004. Con el fin de ampliar la longitud de la serie, y con ello, obtener un número considerable de observaciones, se empleó el método del indicador (Correa, 2003) para realizar el empalme de los datos, usando como período de referencia el nivel de la serie a partir del año 2000, y como variable indicadora, el crecimiento de la serie a precios constantes del año 1994. Así, se obtuvo una muestra de 106 observaciones, que comprende el período 1982:01 a 2008:02.
En la Gráfica 1 se presenta la evolución de la serie en niveles a lo largo del período muestral. El marcado patrón estacional, caracterizado por caídas significativas en el segundo trimestre y fuertes incrementos del producto durante el cuarto trimestre del año, se extrajo a través de la metodología TRAMO-SEATS. La serie del crecimiento trimestral del PIB ajustado estacionalmente es presentada en la Gráfica 2. Para aislar el efecto sobre el nivel medio de la serie asociado a la recesión ocurrida a finales de la década de los 905, se realizó un análisis de intervención tipo cambio de nivel a partir del tercer trimestre del año 98.
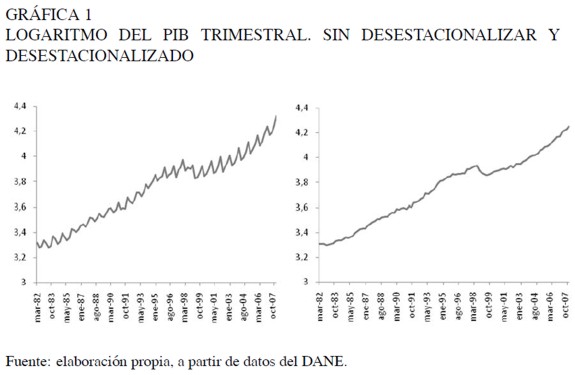
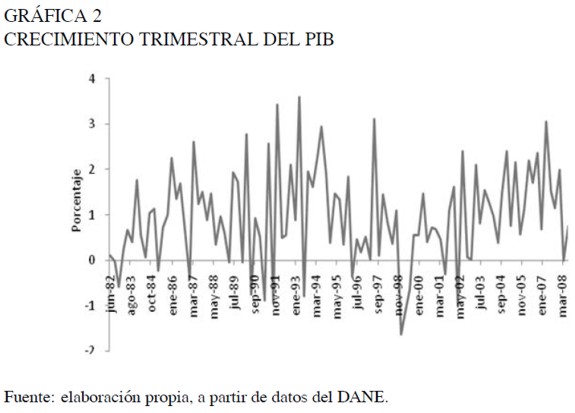
Con el fin de verificar la existencia de no linealidad en la serie, se realizó la prueba propuesta por Tsay para los rezagos de umbral d = 1, . . . , 6. El orden p de la regresión ordenada fue 2, correspondiente al orden autorregresivo del modelo lineal base, que minimiza el criterio de información BIC de Schwarz. El número de observaciones para iniciar el algoritmo de mínimos cuadrados recurrentes fue el sugerido por el autor, que en este caso es equivalente a 12. Adicionalmente, se realizó la prueba empleando distintas configuraciones para los valores de los parámetros iniciales, el Modelo SETAR para el PIB Milena Hoyos, Johanna Ramos, Lorena Vivas 71 número de observaciones en la regresión inicial y los órdenes autorregresivos. El estadístico de prueba F y su respectivo p-valor, para el caso p = 2 y m = 5,12, 20 se presentan en el Cuadro 1.
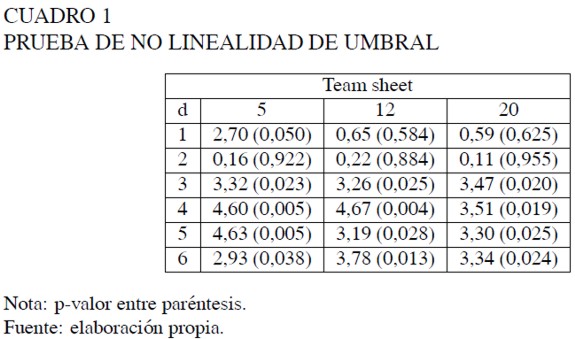
Los resultados indican que existe evidencia estadística de no linealidad para los rezagos 3 a 6, a un nivel de significancia de 5% para todos los valores de m. El menor p-valor del estadístico está asociado al parámetro de retraso d = 4, lo que sugiere a Xt−4 como variable umbral. La evidencia de no linealidad se mantiene para p = 1 al 10% y p = 3 al 1%.
La localización de los umbrales se realizó mediante un diagrama de dispersión entre las estimaciones recurrentes de las razones t del coeficiente de la constante –único parámetro significativo–, y la variable de umbrales.
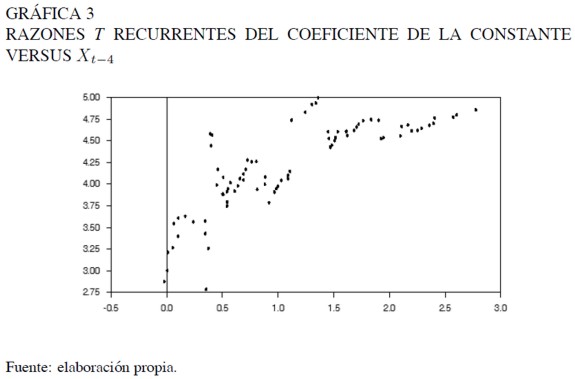
La razón t del coeficiente muestra un salto alrededor de 0,4, sugiriendo la existencia de un umbral. Adicionalmente, se postuló un modelo de tres regímenes con un segundo umbral alrededor de 1,1. Para realizar una búsqueda más detallada de los umbrales y con ello, determinar el mejor modelo para la serie de estudio se usó el criterio de información NAIC. Examinando valores cercanos a 0,4 y 1,1 se consideraron todas las posibles combinaciones ordenadas de los candidatos a umbral y los órdenes autorregresivos. Los resultados para los modelos con los menores NAIC se presentan en el Cuadro 2.
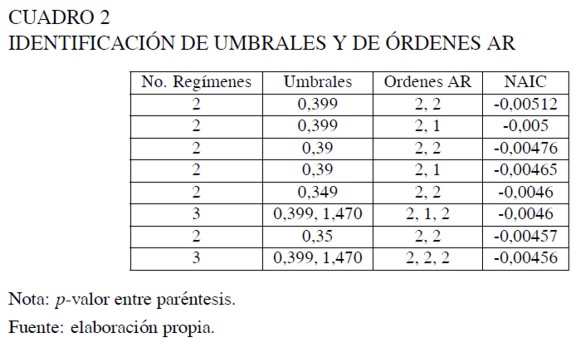
El Cuadro 3 contiene los valores de los parámetros φ (j) i para i = 0, 1, 2 y j = 1, 2 estimados por el método de mínimos cuadrados del modelo SETAR(2,2,2) seleccionado a partir del NAIC.
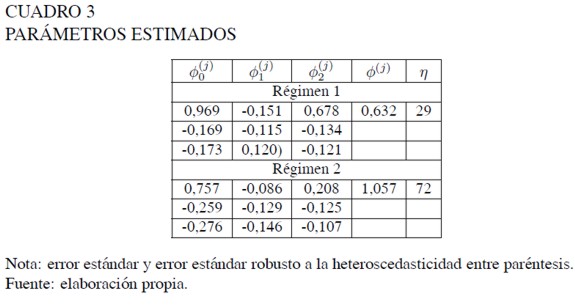
Los coeficientes autorregresivos de rezago 2 y de la constante, a diferencia de los coeficientes asociados al rezago 1, son significativos al 10% para ambos regímenes. Aunque los signos de los parámetros estimados en cada régimen son iguales, difieren en magnitud. Adicionalmente, la serie tiende a permanecer mayor tiempo en el régimen 2, dado que el número de observaciones que pertenecen a éste es mayor que el de las correspondientes al primero de ellos. Además, la media del modelo autorregresivo de cada régimen se encuentra en el que la tasa de crecimiento del PIB toma valores más altos (2,05 y 0,86, respectivamente), aunque la volatilidad es mayor con respecto a la asociada al primer régimen.
La validación del modelo se llevó a cabo a través de la prueba de Ljung-Box sobre la serie de residuales estandarizados y residuales estandarizados al cuadrado unificados y ordenados con respecto al índice temporal de referencia. Los resultados presentados en el Cuadro 4 muestran que no existe evidencia estadística de correlación serial a un nivel de significancia de 1%.
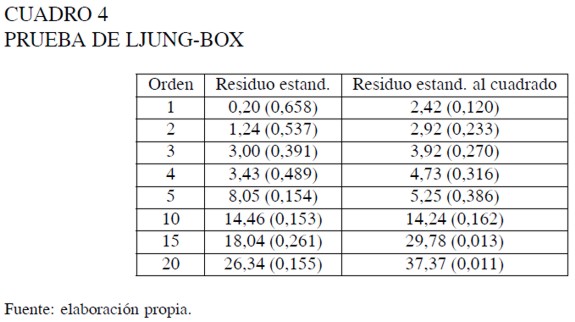
El modelo fue nuevamente estimado eliminando los coeficientes no significativos. Sus resultados son presentados en la ecuación 11 y muestran que el comportamiento dinámico del PIB depende de la magnitud de la tasa de crecimiento registrada un año antes. El primer régimen indica que tasas de crecimiento bajas o negativas son seguidas, cuatro trimestres después, por tasas positivas más elevadas, sugiriendo con ello una recuperación de la economía. Para el caso del segundo régimen, crecimientos positivos moderados son antecedidos por altas tasas de crecimiento.
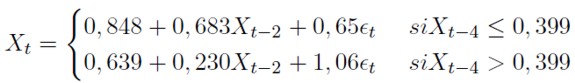
En la Gráfica 4 se destacan los períodos durante los cuales se registró una tasa de crecimiento trimestral inferior al valor del umbral identificado en el modelo (0, 399%). Se evidencia el carácter asimétrico del comportamiento del PIB colombiano, enmarcado en la mayor duración de las fases de altas tasas de crecimiento en comparación con los períodos de "bajas" tasas de crecimiento, cuyo transcurso es igual o inferior a cuatro trimestres, lapso que coincide con la duración de las fases contractivas identificadas por Arango, et al. (2007)6.

Se computaron pronósticos fuera de muestra para este último modelo por medio de simulación deMonte Carlo usando el método rolling que considera todos los orígenes de pronóstico desde 1994:04 hasta 2008:01. Para cada uno de éstos se estimaron los parámetros y se obtuvieron los pronósticos 1 a 12 pasos adelante, realizando 10.000 repeticiones. El mismo procedimiento fue ejecutado sobre diferentes submuestras, cuyos datos de partida corresponden a 1996:03, 1998:02, 2000:01 y 2001:04.
Adicionalmente, se calcularon los pronósticos para un modelo lineal AR(3) y se emplearon funciones de pérdida simétrica (raíz del error cuadrático medio, RECM y error absoluto medio, EAM) para comparar el desempeño de los dos modelos.
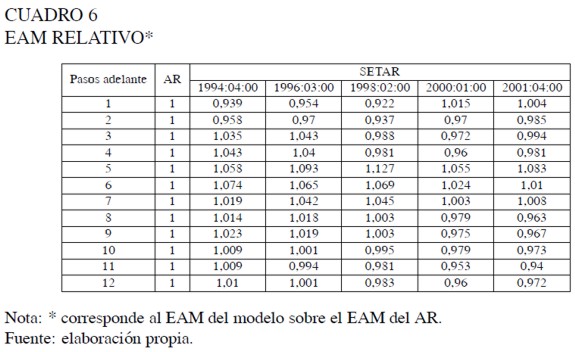
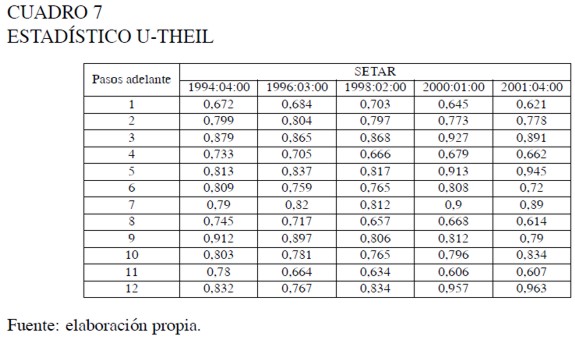
La estadística U-Theil fue computada para contrastar los pronósticos del modelo SETAR con pronósticos ingenuos correspondientes al valor previo observado. Los resultados son presentados en los cuadros 5 a 7.
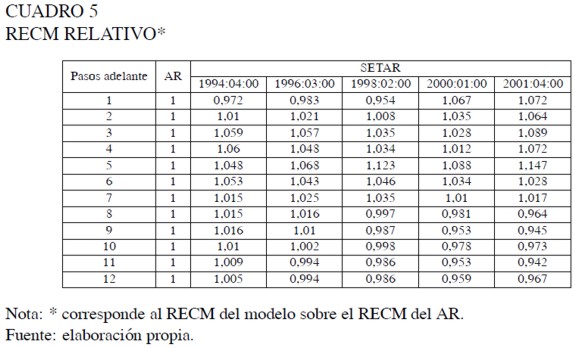
La RECM relativo al modelo AR de los pronósticos dos a siete pasos adelante sugiere un mejor desempeño del modelo lineal para todos los horizontes de predicción. Sin embargo, para k = 1 o k ≥ 8, los resultados difieren dependiendo del origen de pronóstico inicial considerado. Así, por ejemplo, para los tres últimos orígenes, el desempeño de los pronósticos obtenidos por el SETAR es superior con respecto al del modelo lineal, aunque se concluye lo contrario para el origen de pronóstico 1994:04.
Por su parte el EAM, a pesar de mostrar las bondades del modelo SETAR para k = 2 y del AR para k = 5, 6, 7, sugiere que para la mayoría de los horizontes de predicción la superioridad de un modelo sobre el otro, está influenciada por el origen de pronóstico dado. Finalmente, el estadístico UTheil indica que los pronósticos ingenuos son superados por los pronósticos del modelo SETAR para todos los horizontes de predicción y todos los orígenes de pronóstico considerados.
CONCLUSIONES
En este trabajo se ajustó un modelo SETAR de dos regímenes para la tasa de crecimiento del PIB colombiano entre 1982 y 2008, con base en la metodología propuesta por Tsay (1989) y Tong (1990). Los principales resultados muestran evidencia empírica de no linealidad de umbral en la serie asociada a las altas o bajas tasas de crecimiento registradas por su rezago anual y que ésta, permanece más tiempo en el régimen de tasas de crecimiento más elevadas que en el de crecimiento menos acelerado, si bien la volatilidad del término de perturbación asociada al primero de ellos es menor que la encontrada en el caso del segundo régimen.
Por otro lado, se evalúa el desempeño de los pronósticos del modelo, comparándolos con los obtenidos a partir de un modelo lineal autorregresivo, vía contraste de pronósticos de valores dentro de la muestra y a través de valores observados, para diferentes horizontes de predicción. La comparación, basada en el RECMy el EAM, muestra que para diferentes horizontes de predicción, los resultados varían dependiendo del origen de pronóstico que se considere. De esta forma, este documento no aporta evidencia contundente que muestre la superioridad del modelo SETAR en la generación de pronósticos para la serie del PIB colombiano.
NOTAS AL PIE
1 Su confirmación posibilita el uso de modelos adecuados para representar la evolución de la serie, ya que la existencia de asimetrías aporta evidencia para no ajustarla mediante modelos lineales con residuos simétricos (Rodríguez y Badagián, 2004, 2).
2 No existe consenso sobre las bondades de los modelos no lineales, en particular del modelo SETAR en la elaboración de pronósticos. Tsay y Tiao (1994) muestran que los pronósticos a partir de modelos no lineales, durante la fase de contracción, son mejores que los obtenidos por modelos lineales; mientras que el estudio de Teräsvirta (2006) afirma que los pronósticos obtenidos con modelos no lineales parecen no ofrecer mejoras significativas con respecto a los modelos lineales.
3 Algunas de las pruebas comúnmente usadas para validar modelos lineales son utilizadas en este documento para el modelo SETAR.
4 Los resultados de la prueba ADF se registran en el Anexo 1. Se realizaron contrastes usuales de raíces unitarias, Dickey-Fuller aumentados incorporando siete rezagos.
5 La recesión fue provocada, entre otros factores, por el crecimiento desproporcionado del gasto y el consumo privado (que produjo déficits sostenidos y persistentes); el deterioro de los términos de intercambio y los efectos adversos de la crisis financiera internacional, lo cual se tradujo en una fuerte desaceleración de la tasa de crecimiento del producto.
6 En el análisis del índice de producción industrial (IPI) mensual, se pudo concluir que la duración de la etapas contractivas (transcurso entre pico y valle), de los cinco ciclos de negocios completos identificados entre 1980 y 2007, asciende a 12 meses en promedio. Igualmente, al evaluar el comportamiento del PIB trimestral colombiano, se detectaron dos ciclos de negocios completos entre 1977 y 2007, cuyas etapas contractivas presentaron una duración de 2 y 4 trimestres.
ESTADÍSTICAS PRELIMINARES AL AJUSTE DEL MODELO SETAR

REFERENCIAS BIBLIOGRÁFICAS
[1] Arango, L.E. yMelo L.F. (2001). Expansion and contractions in Brazil, Colombia and Mexico: a view through non-linear models. Borrador de economía, 186. Bogotá: Banco de la República de Colombia.
[2] Arango, L.E., et al. (2007). Cronología de los ciclos de negocios recientes en Colombia. Borradores de Economía, 461. Bogotá: Banco de la República de Colombia.
[3] Argandoña, A., et al. (1997). Macroeconomía avanzada II. Madrid: McGraw Hill.
[4] Correa, V., et al. (2003, Abril). Empalme de series anuales y trimestrales del PIB. Revista Económica, 6(1), 77 - 86.
[5] DeLong, J. y Summers, L. (1986). Are Business Cycles Symmetric?. En R.J. Gordon (Ed.), The American Business Cycle: Con-tinuity and Change. (pp. 166-178). Chicago: University of Chicago Press.
[6] Diebold, F. y Rudebusch, G. (1990). A Nonparametric Investigation of Duration Dependence in the American Business Cycle. The Journal of Political Economy, 98(3), 596-616.
[7] Granger, C.W.J. y Teräsvirta, T. (1993).Modelling Nonlinear Economic Relationships. Oxford: Oxford University Press.
[8] Hamilton, J.D. (1989). A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica, 57(2), 357-384.
[9] Hoyos, M. (2007). Expectativas de actividad económica y estructura a plazo de las tasas de interés. Trabajo premiado en el Concurso Andino de Estadística 2007: Contribuciones de la Estadística a la Integración Regional, Junio, Perú.
[10] Misas, M. y Ramírez, M.T. (2005). Depressions in the Colombian economic growth during the XX century: A Markov Switching Regime Model. Borradores de Economía, 340. Bogotá: Banco de la República de Colombia.
[11] Rodríguez S. y Badagián, L. (2004). Dinámicas no lineales y ciclos asimétricos en Argentina, Brasil y Uruguay. Documentos de Trabajo. Asunción: IESTA, Universidad de la República de Uruguay. Extraído el 15 de Octubre de 2008 desde http://www.iesta.edu.uy/publicaciones/.
[12] Teräsvirta, T. y Anderson, H. (1992). Characterizing nonlinearites in business cycles using smooth transition autoregressive models. Journal of Applied Econometrics, 7, 119-136.
[13] Teräsvirta, T., et al. (2006). Forecasting Economic Variables with Nonlinear Models. En G. Elliott, C.W.J. Granger & A.G.Timmermann (Ed.), Handbook of Economic Forecasting (pp. 413-453). Oxford, Inglaterra: Elsevier B.V.
[14] Tong, H. (1978). On a ThresholdModel. En C.H. Chen (Ed.), Pattern Recognition and Signal Processing (pp. 575-586). Amsterdam, Holanda: Sijhoff & Noordhoff.
[15] Tong, H. (1990). Nonlinear Time Series, A Dynamical System Approach. Oxford: Oxford University Press.
[16] Tsay, R.S. (1989). Testing and modeling threshold autoregressive processes. Journal of Forecasting, 84, 231-240.
[17] Tiao, G. & Tsay, R. S. (1994). Some advances in non-linear and adaptive modeling in time-series. Journal of Forecasting, 13, 109-131.