EN BUSCA DE UN MODELO BENCHMARK UNIVARIADO PARA PREDECIR LA TASA DE DESEMPLEO DE CHILE
Javier Contreras-Reyes*
Byron Idrovo*
*Magíster en Estadística, se desempeña como estadístico en el Centro de Modelamiento Matemático del Departamento de Ingeniería Matemática de la Universidad de Chile (Santiago de Chile, Chile). E-mail: jcontreras@dim.uchile.cl. Dirección de correspondencia: Blanco Encalada 2002 (Santiago de Chile, Chile).
*Magíster en Economía, se desempeña como economista en la Gerencia de Estudios de la Cámara de la Construcción (Santiago, Chile). E-mail: bidrovo@cchc.cl. Dirección de correspondencia: Marchant Pereira 10, Providencia (Santiago de Chile, Chile).
Este artículo fue recibido el 23 de septiembre de 2010, la versión ajustada fue recibida el 3 de mayo de 2011 y su publicación aprobada el 3 de junio de 2011.
Resumen
En este trabajo se analiza la precisión y la estabilidad de las predicciones de la tasa de desempleo de Chile, obtenidas de una familia de modelos SARIMA, entre febrero de 1986 y febrero de 2010. Las proyecciones SARIMA son comparadas con las provenientes de modelos univariados, incluyendo los benchmarks predictivos. Simultáneamente, se ajustó un modelo ARFIMA (Autorregresive Fractionary Integrated Moving Average), debido a los signos de persistencia que muestra el indicador de desempleo en su comportamiento; sin embargo, a partir de los métodos de estimación de Reisen (1994), Geweke et al. (1983) y Whittle (1962) se obtuvieron parámetros de integración mayores que 0.5, lo que empíricamente sustenta el tratamiento de la tasa de desempleo como una serie no estacionaria. La evaluación de la capacidad predictiva de los modelos se centra en las proyecciones fuera de muestra de 1, 6 y 12 meses hacia adelante. Los resultados indican que el RECM fuera de muestra de las proyecciones SARIMA es menor que el de los métodos univariados considerados.
Palabras clave: tasa de desempleo, SARIMA, ARFIMA, benchmarks predictivos, Chile. JEL: E24, J21, E27, C15, C20.
Abstract
In this work the precision and stability of the forecasts of Chile's unemployment rates are analyzed. Said models were obtained by a family of SARIMA (Seasonal Autoregressive Integrated Moving Average) models, between February 1986 and February 2010. The SARIMA projections are compared with the ones originating from univariate models, including the benchmark predictive ones. Simultaneously and ARFIMA (Autoregressive Fractionally Integrated Moving Average) model was adjusted, owing to the signs of persistence that the unemployment indicator shows in its behavior; nevertheless, starting from the estimation methods developed by Reisen (1994), Geweke et al. (1983), and Whittle (1962) integration parameters greater than 0.5 were obtained, which empirically upholds the proposal of addressing the unemployment rate as a non stationary series. The evaluation of the predictive capacity of the models is centered in the forecasts out of the sample of 1, 6, and 12 months from then on. The results indicate that the RECM out of the sample of the SARIMA projections is less than the one from the considered univariate methods.
Key words: unemployment rate, SARIMA, ARFIMA, Benchmark, forecast, Chile. JEL: E24, J21, E27, C15, C20.
Rèsumè
Dans ce travail on évalue la précision et la stabilité des prédictions du taux de chômage au Chili, obtenues à travers une famille de modèles SARIMA, entre février 1986 et février 2010. Les projections SARIMA sont comparées avec celles des modèles univariés, en incluant les benchmarks prédictifs. Simultanément, on a adapté un modèle ARFIMA (Autorregresive Fractionary Integrated Moving Average), grâce aux signes de persistance qui montre le taux de chômage dans son comportement. Cependant, à partir des méthodes d'estimation de Reisen (1994), Geweke et al. (1983) et Whittle (1962) on a obtenu des paramètres d'intégration supérieurs à 0,5, ce qui permet de supporter empiriquement le traitement du taux de chômage en tant que série non stationnaire. L'évaluation de la capacité de prédiction des modèles se concentre sur les projections hors -échantillon le long des durées de 1, 6 et 12 mois. Les résultats indiquent que le RECM hors-échantillon des projections SARIMA est plus petit que celui des méthodes univariées considérées.
Mots clés : taxe de chômage, SARIMA, ARFIMA, benchmarks prédictifs, Chili. JEL: E24, J21, E27, C15, C20.
La motivación de este estudio radica en la necesidad de contar con benchmarks basados en modelos univariados de series de tiempo para predecir la tasa de desempleo de Chile. En el ámbito económico, esta clase de modelos constituyen atractivos benchmarks para evaluar la capacidad predictiva de modelos estructurales, en los que interactúan múltiples variables y cuya forma funcional está basada en la teoría económica. La sencillez del mecanismo de identificación, estimación y predicción que caracteriza a los modelos univariados de series de tiempo, es la razón principal por la que son frecuentemente utilizados en la literatura.
Por otro lado, predecir la tasa de desempleo es relevante, debido a su estrecho vínculo con el ciclo económico. Básicamente, al ser la mano de obra un factor substancial para la producción de bienes y servicios, es una parte importante del aparato productivo de la economía. Asimismo, de acuerdo a la ley de Okun1, los cambios en el ciclo económico están correlacionados negativamente con la tasa de desempleo, es decir, a mayor (menor) crecimiento económico, menor (mayor) desocupación laboral. En este sentido, la tasa de desempleo publicada mensualmente por el Instituto Nacional de Estadísticas (INE) es un indicador natural de alerta temprana de la actividad económica agregada. Particularmente, Bergoing et al. (2005) sostienen que la dinámica del empleo es una variable que incide fuertemente en la economía chilena. Igualmente, los modelos estructurales utilizados para la medición de la tasa de crecimiento tendencial de la economía, comúnmente incorporan la relación entre los cambios del desempleo y los cambios en la producción. Por lo tanto, proponer benchmarks precisos para predecir la trayectoria de la tasa de desempleo, constituye un legítimo aporte para establecer una forma de comparación de la habilidad predictiva de los modelos de estructura económica.
En este contexto, el presente trabajo investiga la capacidad predictiva de los procesos SARIMA (Seasonal Autoregressive Integrated Moving Average) que además de ajustar los componentes cíclico y estacional propios de una serie económica como es la tasa de desempleo de Chile, se caracterizan por ser modelos fáciles de identificar, estimar y predecir. Se utilizó información disponible desde febrero de 1986 hasta febrero de 2010 (289 observaciones)2. Alternativamente, se ajustó un modelo ARFIMA (Autorregresive Fractionary Integrated Moving Average), debido a que el desempleo muestra cierta persistencia en su comportamiento, lo que presumiblemente responde al lento ajuste del salario real frente a los distintos estados del ciclo económico.
A partir de los métodos de estimación de Reisen (1994), Geweke et al. (1983) y Whittle (2002) se obtuvieron parámetros de integración mayores que 0,5, lo que empíricamente sustenta el tratamiento del desempleo como una serie no estacionaria (ver Anexo 1a ). Esto último podría resultar un tanto extraño al economista no familiarizado con la literatura predictiva de procesos univariados. Sin embargo, considerar la existencia de una o más raíces unitarias en la tasa de desempleo, elimina la incertidumbre paramétrica, ya que los modelos de series de tiempo tienden a ser parsimoniosos (García y Pincheira, 2006).
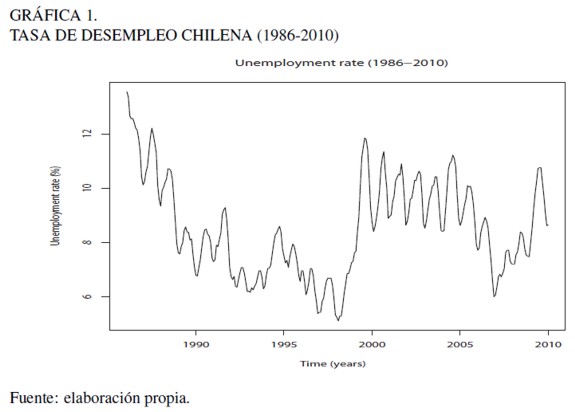
En la literatura económica se distinguen dos posturas para tratar de explicar el comportamiento del desempleo de Chile. Una de ellas es que la evolución de esta variable obedece predominantemente a shocks de productividad, lo que promueve una conducta cíclica en el empleo (Cowan et al., 2005) La disminución sistemática de la tasa de desempleo durante el período 1986-1998 (Gráfica 1), coincide con una alta acumulación de mano de obra y un crecimiento significativo de la productividad total de factores – en línea con la recuperación de las libertades civiles, mejores términos de intercambio, mayor disponibilidad de capital externo, estabilidad macroeconómica y mercados financieros más profundos. El salto discreto del desempleo en 1999 responde, básicamente, al efecto recesivo de la crisis asiática – que incidió en el menor nivel del producto potencial. En este contexto, la persistente disminución de la tasa de desempleo durante más de una década, seguida por un significativo cambio de su nivel y tendencia, hacen de ella un proceso estadísticamente no estacionario en niveles, pero sí en primeras diferencias.

El segundo planteamiento establece que además de los posibles shocks a la productividad en Chile, se debe considerar el efecto de nuevas políticas en el mercado laboral (Rodríguez, 2007; Martínez et al., 2001; Brown et al., 1975), tales como: los aumentos del salario mínimo en el período 1998-2000 y la reforma laboral establecida a fines del año 2001 -en la cual las normativas al código del trabajo incluyen una ley que disminuye el número de horas semanales máximas permitidas (de 48 a 45) y que entra en vigencia desde 2005. Así, la interacción entre los mayores costos de contratación para las empresas y el costo de oportunidad de permanecer inactivo para las personas, se tradujo en una tasa de desempleo persistentemente alta con respecto a la observada durante la época de oro (1986-1998).
Posiblemente, la yuxtaposición de ambos efectos (shocks de productividad y de intervención de política), implicaría la existencia de heterogeneidad en la evolución histórica de la tasa de desempleo. Por lo que la matriz de covarianza de su componente estacional también podría ser inestable en el tiempo. De este modo, no se descarta que lo anterior haga del desempleo de Chile un proceso regular de densidad espectral no racional con dos raíces unitarias: una en el componente no periódico y otra en el bloque estacional. Por esta razón, ambas raíces unitarias son consideradas y tratadas en este trabajo, con el objetivo de identificar el mejor modelo SARIMA para predecir el desempleo.
Por otra parte, no existe consenso en la literatura con respecto a la forma en que se debería seleccionar el número de rezagos de los modelos autorregresivos. Mientras algunos autores escogen rezagos basados en el criterio de información de Akaike (AIC) (Stock y Watson (SW), 2003, 2006), otros se basan en el criterio de información Bayesiano (BIC) (Elliot y Timmermann, 2008). Ambos criterios, que en principio seleccionan modelos de acuerdo con el ajuste dentro de la muestra, difieren en la penalización que hacen a los parámetros adicionales que deberán ser estimados en el modelo.
Dado lo anterior, el orden de rezagos de los modelos univariados de series de tiempo, están basados en los criterios mencionados anteriormente; mientras que el método descriptivo de selección fundamentado en el error cuadrático medio de la predicción (ECM) y el estadístico propuesto por Giacomini y White (2006) son utilizados para evaluar si el modelo SARIMA es capaz de dominar en términos de precisión y estabilidad predictiva a un conjunto de modelos alternativos de series de tiempo univariados – extensamente utilizados en la literatura económica.
Las predicciones de la tasa de desempleo se realizan en un período de 12 años (enero de 1999 a febrero de 2010). Este lapso en particular considera el efecto adverso de la crisis asiática de 1999, y el posterior cambio de régimen de meta inflacionaria y de superávit estructural en la economía chilena. La evaluación de la calidad predictiva de los modelos se centra en las proyecciones fuera de muestra de 1, 6 y 12 meses hacia adelante. En este sentido y siguiendo el estudio de García y Pincheira (2006) sobre modelos de predicción aplicados a la inflación de Chile, el presente trabajo busca contar con benchmarks predictivos para la tasa de desempleo chileno.
Entre los estudios que consideran modelos univariados como benchmarks predictivos de la tasa de desempleo se encuentra el de Gomes y Reis (2009). Estos autores plantean modelos ARFIMA, al mismo tiempo que realizan pruebas de raíz unitaria con quiebres estructurales para examinar la persistencia del desempleo en la zona metropolitana de la ciudad de San Pablo en Brasil. Entre los principales hallazgos, descartan la hipótesis de que la tasa de desempleo de la ciudad sea estacionaria, ya que la estimación del parámetro de integración fraccionaria resultó mayor que 0,5 durante el período mensual de 1985-2008. Por lo que concluyen que los modelos de la familia SARIMA son apropiados para modelar la dinámica del desempleo.
Para el caso de Rumania, Dobre y Alexandru (2008) modelan la trayectoria mensual de la tasa de desempleo usando la metodología de Box y Jenkins (1970), para los años 1998-2007. Los resultados que se derivan del estudio empírico revelan que el modelo más adecuado para replicar el desempleo en Rumania es un ARIMA (2, 1, 2).
Para el caso de Chile, existe poca evidencia de la aplicación de modelos univariados de series de tiempo para predecir la tasa de desempleo, ya que los mayores esfuerzos se han concentrado en identificar las variables explicativas y predecir con base en éstas. Por esto, la literatura trata, principalmente, modelos multivariados de estructura económica, los cuales no siempre son capaces de vencer homogéneamente en el tiempo a sencillos benchmarks univariados3. Este hallazgo coloca un reto a los posteriores intentos de predecir la tasa de desempleo: los nuevos modelos deben ser capaces de vencer al menos a un simple proceso autorregresivo de primer orden.
Los resultados del presente trabajo indican que el ECM (RECM) fuera de muestra de las proyecciones SARIMA es menor que el de los métodos univariados. En particular, el modelo SARIMA permite obtener proyecciones que son estadísticamente más precisas que las de los benchmarks univariados, considerados para todos los horizontes analizados. Estos resultados fueron coherentes con el test de Giacomini y White (2006), el cual está orientado a evaluar un método de predicción y no un modelo de diagnóstico. Por último, si bien no se ahonda en las razones que se encuentran detrás del satisfactorio comportamiento predictivo, éste se asocia a la imposición de dos raíces unitarias en la tasa de desempleo, lo que provee predicciones más precisas.
El documento está organizado en tres secciones de la siguiente forma. En la primera se discute la metodología, en el segundo segmento se analizan los resultados obtenidos y se realizan las comparaciones de los diversos modelos utilizados en la literatura; en el tercer apartado se formulan las conclusiones.
METODOLOGÍA
Desde febrero de 1986 –primer registro de desempleo publicado por el INE– la tasa de desempleo chilena ha mostrado un comportamiento cíclico y estacional muy característico. En épocas de auge (parte más alta del ciclo económico) el desempleo disminuye considerablemente hasta ubicarse por debajo de su promedio histórico. Por el contrario, frente a escenarios de crisis dicha variable tiende a expandirse significativamente con respecto a su medida de tendencia central. Con relación al componente estacional, la tasa de desempleo alcanza su mayor nivel en los meses de invierno –siendo julio y agosto los meses más predominantes de cada año. Esto se debe en parte, a la postergación de las obras de infraestructura y edificación – altamente intensivas en la utilización de mano de obra–, ante condiciones climáticas poco propicias para el desarrollo normal de estas actividades.
En este contexto, es posible modelar la tasa de desempleo como un proceso del tipo ARIMA (p, d, q) × (P,D,Q)s. Este modelo captura la particularidad estacional y cíclica de la serie – la parte cíclica es la que se asocia al componente autorregresivo y de media móvil.
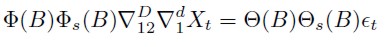 | [1] |
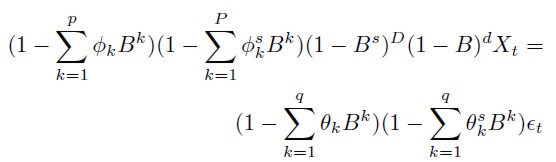 | [2] |
Donde, Φ(B) es un polinomio de coeficientes, con operador de rezagos B del componente autorregresivo AR; y Φs(B) es análogo al caso anterior, pero aplicado al proceso autorregresivo de la parte estacional SAR. Θ(B) y Θs(B) son los polinomios de coeficientes del proceso de media móvil MA y su símil estacional SMA.
Se sospecha que la tasa de desempleo es no estacionaria, debido a los cambios significativos de media y varianza durante las fases de boom y recesión económica. De igual forma, se presume que el tramo ARIMA del componente periódico (o estacional) también es no estacionario, ya que existen factores (propios del efecto calendario) que indirectamente podrían acentúar la estacionalidad de la serie – por ejemplo, la composición de los días de la semana.
En resumen, el procedimiento utilizado para modelar la serie de la tasa de desempleo es:
1. Se estimó la función de autocorrelación (ACF) de la serie y se observó que convergía hiperbólicamente a cero. Al descartar la posibilidad de que sea estacionaria con integración fraccionaria (ver Anexo 1), se optó por transformar la serie tomando una diferenciación.
2. Se obtuvo nuevamente la ACF y se encontró un patrón estacional con un comportamiento sinusoidal de larga memoria, lo cual es típico en variables que muestran alta persistencia en su trayectoria. Por lo tanto, se optó por diferenciar en doce meses la serie obtenida en el paso anterior.
3. Basándose en los criterio de Akaike y BIC, se seleccionó el mejor modelo SARIMA, estimado mediante Máxima Verosimilitud (ML). Los residuos del modelo resultaron ruido blanco – según el test de Box-Ljung.
En el período 1986-1997 la tasa de desempleo mantuvo una tendencia a la baja – con un promedio histórico de 8,1%. Este fenómeno es coherente con el nivel potencial de crecimiento económico observado durante dicho período – en torno a 7,8% (Chumacero, 1996). Dada la característica de la serie, cualquier predicción de desempleo, con base en estos datos, difícilmente habría dado cuenta de un fuerte cambio de tendencia, como la observada durante la crisis asiática (1998- 1999). Para entonces, el desempleo aumentó en forma persistente hasta llegar a su máximo nivel de 11,9% en agosto de 1999, para luego mantenerse oscilante en torno a 9,2% en los siguientes ocho años. Durante la post-crisis asiática, la actividad económica se caracterizó por su bajo desempeño – con un crecimiento potencial de sólo 5% (Johnson, 2001)–, relativo a la pronta recuperación experimentada por los países del sudeste asiático. Estos sucesos dieron orígen al debate sobre la aparente persistencia de la actividad económica y por ende del empleo. Algunos autores sostienen que la dinámica del empleo es uno de los factores que incide altamente en el prolongado deterioro de la economía (Bergoeing et al., 2005).
A partir del segundo semestre de 2008, tras los efectos de la crisis financiera internacional, la tasa de desempleo chilena tendió nuevamente al alza; incluso, alcanzó niveles similares a los observados durante crisis asiática. Esto refleja en parte, un cierto grado de homogeneidad en la reacción del mercado laboral frente a shocks externos, al menos, durante la recesión de 1999 y la más reciente.
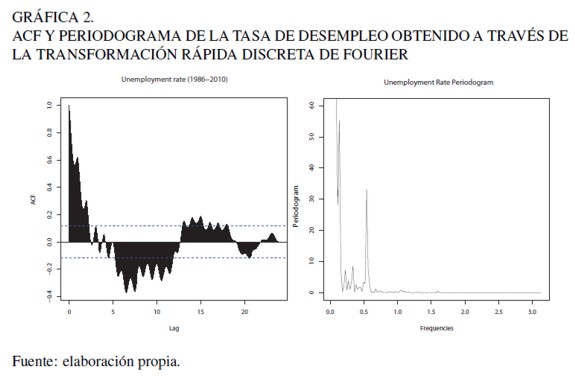
En este contexto y sumando las características de no estacionariedad de la tasa de desempleo, se propone un análisis basado en un modelo de series de tiempo del tipo SARIMA para predecir la tasa de desempleo mensual en el corto plazo. Basado en el análisis de densidad espectral, se encuentra que las discontinuidades de la serie de desempleo son puramente cíclicas. El periodograma de la Gráfica 2 destaca un peack en torno a 0, 5 (2π /0,5 ≈ 12 meses), lo que refleja la predominancia del componente cíclico de la serie, validando empíricamente la especificación del modelo propuesto. Esto a su vez permite que el shock de la crisis asiática sea un argumento válido para simular la crisis de 2010. Es más, las similitudes encontradas entre las trayectorias de los niveles de desempleo de la crisis asiática versus la crisis de 2010 ponen de manifiesto la significativa inercia del mercado laboral, al punto de que los shocks materializados durante la crisis asiática, presuntamente, podrían ser replicados en la actualidad.
Por último, a diferencia de otros estudios en los que se modela una estructura económica para ajustar la tasa de desempleo nacional, el presente estudio permite que los propios datos temporales de la variable desempleo revelen las características de la estructura probabilística subyacente. En este sentido, el presente documento no indaga sobre los factores que están detrás de la posible rigidez del mercado laboral; su objetivo es modelar y proyectar la tasa de desempleo con base en su propia historia, es decir, utilizando únicamente la significativa correlación con el pasado.
Por otra parte, la elevada persistencia y volatilidad de la serie de desempleo hizo que cualquier intento de estabilización mediante la aplicación de funciones de transformación de la variable de tipo Box Cox, resultara infructuosa. La función de autocorrelación (ACF) de la Gráfica 2 muestra un prolongado decaimiento a medida que aumentan los rezagos de tiempo, por lo que en primera instancia se sospecha que podría tratarse de un proceso de larga memoria del tipo ARFIMA. Sin embargo, a partir de los métodos de estimación de Reisen (1994), Geweke et al. (1983), y Whittle (1962) se obtuvieron parámetros de integración mayores que 0, 5, lo que empíricamente sustenta el tratamiento de la tasa de desempleo como una serie no estacionaria (ver Anexo 1).
Análisis de tendencia y estacionalidad del ajuste SARIMA
Tras descartar la posibilidad de que la tasa de desempleo sea estacionaria con integración fraccionaria, se optó por la primera diferenciación. En otras palabras, para eliminar la tendencia estocástica, se procedió a diferenciar la serie una vez. En la Gráfica 3 (primer gráfico de izquierda a derecha) se muestra la pérdida de tendencia, aunque la variabilidad producida por la estacionalidad de la serie persiste al observar la función de autocorrelación de la serie ajustada (segundo gráfico). Dado que eurísticamente la estacionalidad es sinónimo de no estacionariedad, se realizó el respectivo ajuste estacional de la serie.
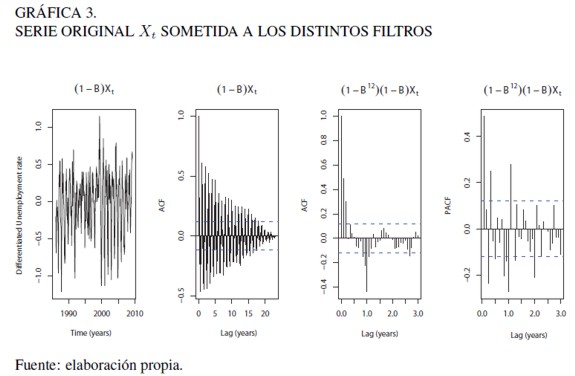
De este modo, la Gráfica 3 muestra las ACF y la función de autocorrelación parcial (PACF) de la tasa de desempleo después de controlar por su tendencia estocástica y estacionalidad (tercer y cuarto gráfico de izquierda a derecha). A partir de la ACF se determinó que existen los siguientes peacks: uno en la parte MA estacional (esto es cada 12 meses por ser la serie de frecuencia mensual) y cuatro en la parte MA de los parámetros ARIMA de la serie.
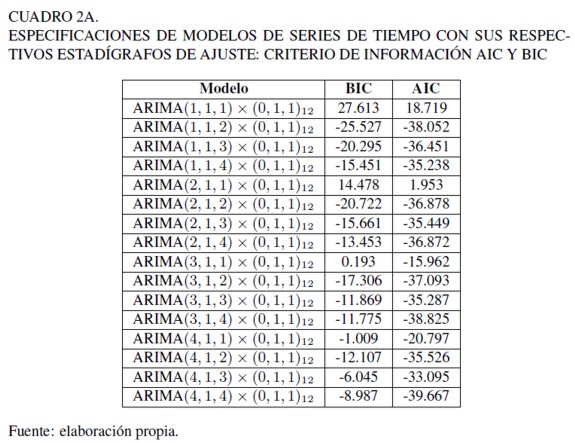
En el gráfico PACF es posible notar que existen los siguientes saltos: dos en la parte AR estacional (períodos 12 y 24, respectivamente) y tres significativos en la parte AR de los parámetros ARIMA de la tasa de desempleo. De esta forma, se determina un modelo preeliminar: ARIMA(3, 1, 4) × (2, 1, 1)12, estimado por el método de máxima verosimilitud (MV). No obstante, al estimar los parámetros de este modelo no se encontró significancia para el componente AR estacional según el estadístico t-student (ver Cuadro 3A). Tomando en consideración el principio de parsimonia, se decidió estimar el modelo ARIMA(1, 1, 2) × (0, 1, 1)12, el cual obtuvo valores AIC y BIC (-38,05 y -25,53) menores que los inicialmente propuestos (-37,06 y -16,16), como lo muestra el Cuadro 2A.
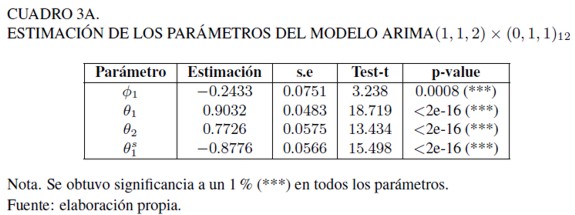
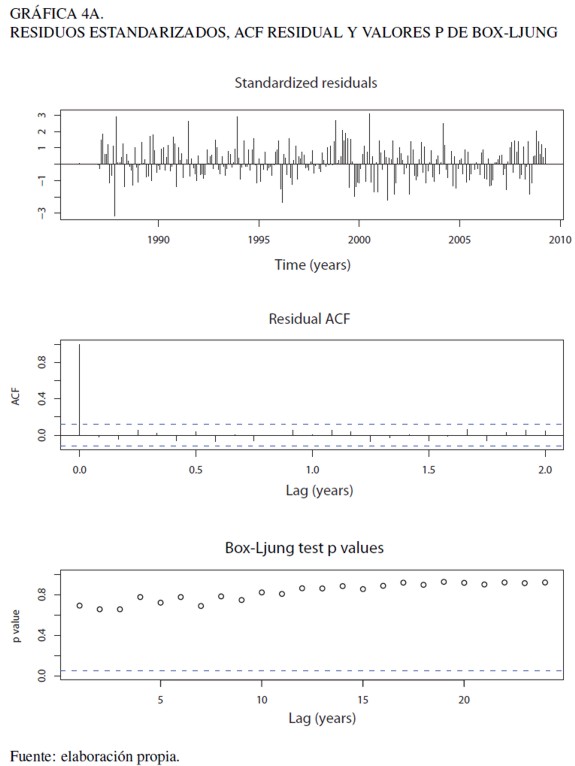
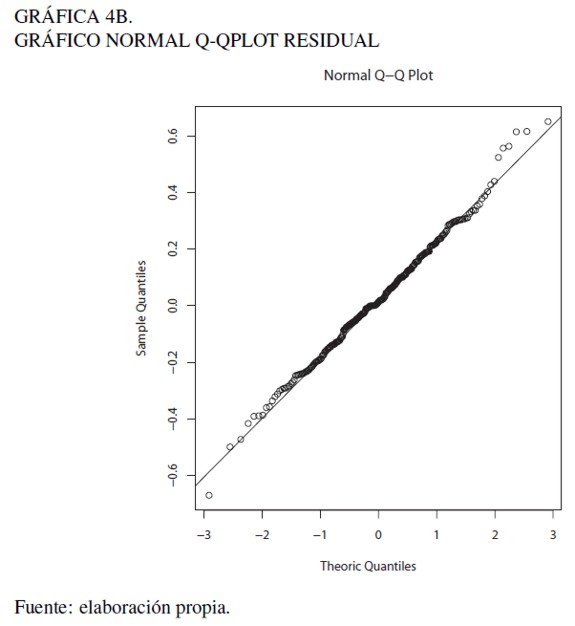
Todos los parámetros del modelo ARIMA(1, 1, 2)× (0, 1, 1)12 resultaron significativos a un nivel de confianza de 95% y con errores ruido blanco distribuidos normalmente. Por otro lado, en la Gráfica 4A se puede apreciar que el test de BoxLjung muestra que los valores p asociados a los residuos del modelo son mayores que el error de confianza α = 0,05, para un rezago equivalente a 24 meses y las autocorrelaciones residuales se concentran dentro de las bandas de Bartlett, por lo que se concluye que los residuos no están correlacionados. Además, se muestra que los residuos en gran medida se concentran en la recta normal y el test de normalidad Shapiro-Wilk arroja un valor p de 0,433 (W = 0,994), lo cual no rechaza la hipótesis nula de normalidad residual. De esta forma, los supuestos de normalidad y de ruido blanco de los residuos son coherentes con el no rechazo de los test (Gráfica 4B).
Evaluación de habilidad predictiva
Un método de proyección será mejor que otro en la medida que tenga menor RECM. Para comparar estadísticamente la diferencias de habilidad predictiva entre los modelos propuestos, se hará uso del paradigma de evaluación propuesto por Giacomini y White (2006). Este test está orientado a evaluar un método de predicción y no un modelo de diagnóstico, por ende, no considera incertidumbre paramétrica, lo cual es útil si se desea comparar modelos anidados provenientes de un modelo SARIMA. El test GW atribuido a Diebold-Mariano (1995) se construye a partir de la diferencia ΔLnT = Li(y) – Lj(y) donde Li(y) =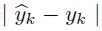 , k = 1, … , T, el cual corresponde al error de predicción del modelo i ≠ j. Se propone contrastar H0: E[ΔL] = 0 vs H1: E[ΔL] > 0, a partir del siguiente estadístico4:
, k = 1, … , T, el cual corresponde al error de predicción del modelo i ≠ j. Se propone contrastar H0: E[ΔL] = 0 vs H1: E[ΔL] > 0, a partir del siguiente estadístico4:
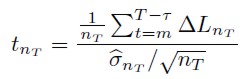 | [3] |
Siendo nT = T – τ – m + 1, T el tamaño total de la muestra, τ el horizonte de predicción y m la observación en que comienza las ventanas móviles. Para τ = 1, se utiliza una estimación para 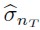 a partir de la estimación de
a partir de la estimación de 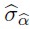 asociado al modelo de regresión simple
asociado al modelo de regresión simple 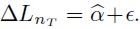 Sin embargo, para horizontes τ > 1 se permite usar estimador HAC de Newey-West (1994).
Sin embargo, para horizontes τ > 1 se permite usar estimador HAC de Newey-West (1994).
A partir de esta herramienta estadística, se compara el modelo SARIMA versus distintos benchmarks: AR(1), IMA(1), ARMA(1,1), modelos ARMA y ARIMA con menores AIC y BIC.
RESULTADOS
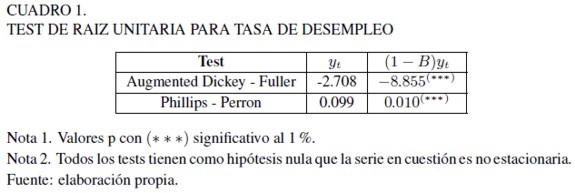
En primer lugar, se encontró que el proceso que caracteriza a la tasa de desempleo es no estacionario, por lo que se ajustó un modelo autorregresivo integrado de primer orden. Los estimadores de Reisen-Geweke y Porter-Hudak arrojaron valores en torno a 1 para el parámetro de integración, mientras que para la estimación de Whittle, se obtuvo un parámetro fraccionario cercano al 0,5 para cualquier especificación de las componentes AR y MA. Al descartar la posibilidad de que la tasa de desempleo sea estacionaria con integración fraccionaria, se consideró la presencia de una tendencia estocástica. Es más, los test de raíz unitaria de Dickey-Fuller aumentado y Phillips-Perron confirman la característica no estacionaria de la variable de interés. El Cuadro 1 muestra los valores p con niveles de significancia de 1% (* * *). Ambos tests tienen como hipótesis nula que la serie en cuestión es no estacionaria. En esta línea, se plantearon modelos autorregresivos y de media móvil aplicados a la variable de desempleo diferenciada en primer orden.
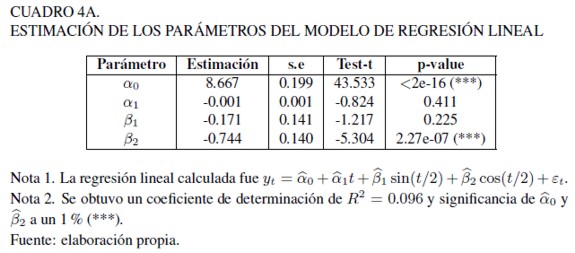
Adicionalmente, se ajustó un modelo de regresión lineal con tendencia y estacionalidad sinusoidal determinísticas âesto considerando la frecuencia encontrada en el periodograma (ver Gráfica 1 A). A partir de la información del Cuadro 4 A se puede decir que los parámetros asociados a la tendencia y periodicidad senoseoidal no son significativas y que según el test de Box-Ljung, los residuos no son ruido blanco. Se concluye que un modelo determinístico de estas características no es adecuado ni para el ajuste ni para realizar predicciones de la tasa de desempleo.
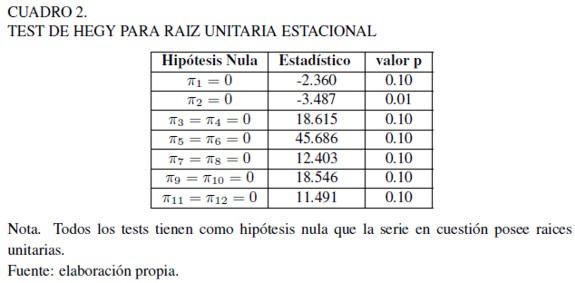
Por otra parte, se testeó la presencia de raíces unitarias estacionales mediante el test de Hylleberg-Engle-Granger-Yoo (HEGY) (Hylleberg, Engle, Granger y Yoo, 1990). Un primer resultado (H0 : π1 = 0) confirma la presencia de raíz unitaria no estacional en relación con lo obtenido por los test de Dickey-Fuller y Phillips-Perron. De igual forma, se comprobó estadísticamente una alta persistencia en el componente períodico del desempleo, al no rechazar la hipótesis nula de raíz unitaria estacional (ver Cuadro 2 ).
En este contexto y sumando las características de no estacionariedad de la tasa de desempleo, se efectuó un análisis basado en un modelo de series de tiempo del tipo SARIMA. De esta forma y tomando en consideración el criterio de AIC y BIC, se obtuvo un modelo ARIMA(1, 1, 2) × (0, 1, 1)12. A partir de este modelo se calculó el período de permanencia de una perturbación en la tasa de desempleo, empleando la función de impulso-respuesta:
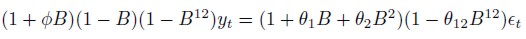 | [4] |
Definiendo
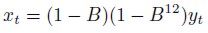 | [5] |
Se obtiene la siguiente expresión:
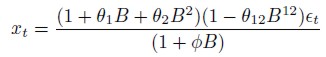 | [6] |
Realizando la descomposición de Wald para el denominador se tiene que:
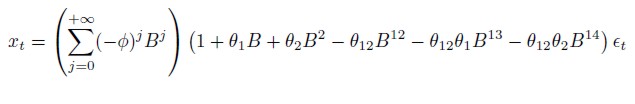 | [7] |
Definiendo una perturbación εt = 1, la función de impulso-respuesta del modelo está dada por:
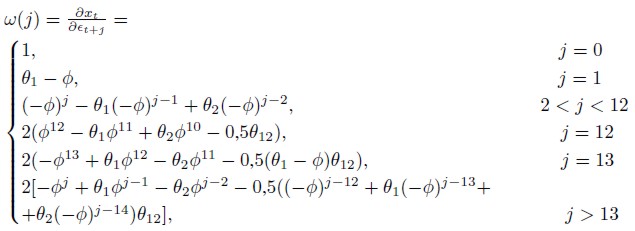 |
Se puede apreciar en la Gráfica 5 la elevada persistencia de una perturbación en la serie. Según el modelo propuesto, la persistencia en la dinámica de la tasa de desempleo podría prolongarse por más de un año.
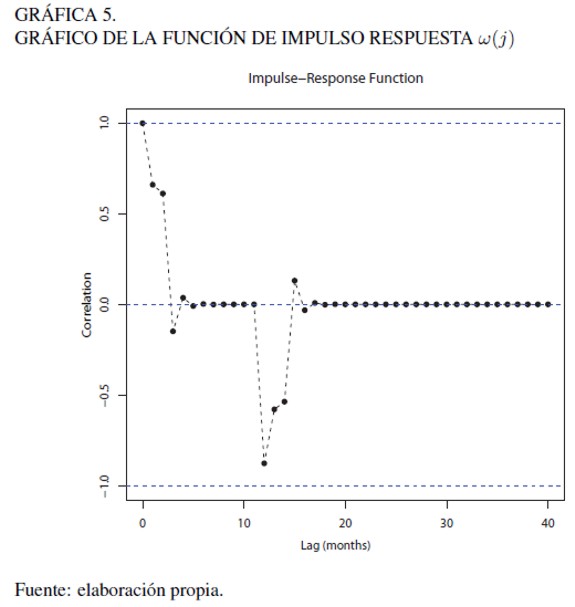
Con relación a la calidad de las predicciones, los cuadros 5A , 6A y 7A del anexo muestran los resultados del test de GW aplicado a los modelos mencionados en la sección de “evaluación de la habilidad predictiva” y al modelo SARIMA. Para cada celda se muestra el valor p asociado al test, en donde un valor menor a 0,05 (si se utiliza un nivel de confianza del 95 %) indica que el modelo en la fila posee mayor RECM que el de columna. Una simple inspección por los cuadros permite apreciar que en todos los casos y para los 3 horizontes considerados, el modelo propuesto SARIMA no posee mayor ECM que los benchmarks tradicionales y más aún, en todos los casos los valores p son cercanos a 1, lo cual indica que para un 95% en el test a una cola los benchmarks tradicionales no poseen menor ECM que el modelo propuesto.
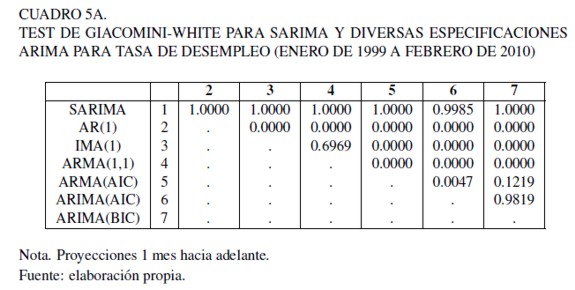
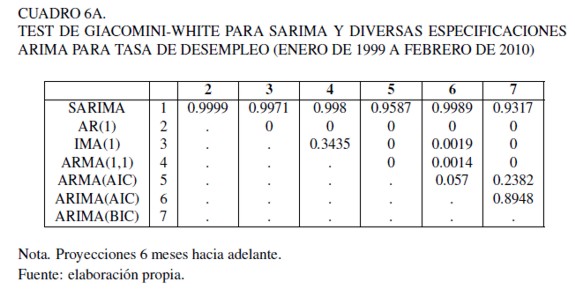
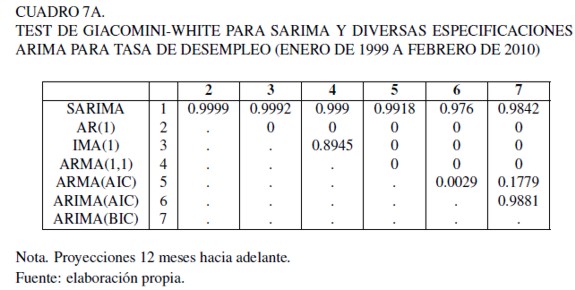
Con el propósito de hacer más expedita la exposición, es conveniente comparar estos resultados con el Cuadro 8 A del anexo, el cual muestra los valores RECM de cada modelo, para los 3 horizontes de predicción. Se puede apreciar que en general los valores RECM asociados a los modelos aumentan a medida que crece el horizonte de predicción, sin embargo, el RECM del modelo propuesto SARIMA se mantiene siempre bajo. Además, se evidencia que el benchmark ARIMA obtenido por BIC, es el modelo con el segundo menor ECM.

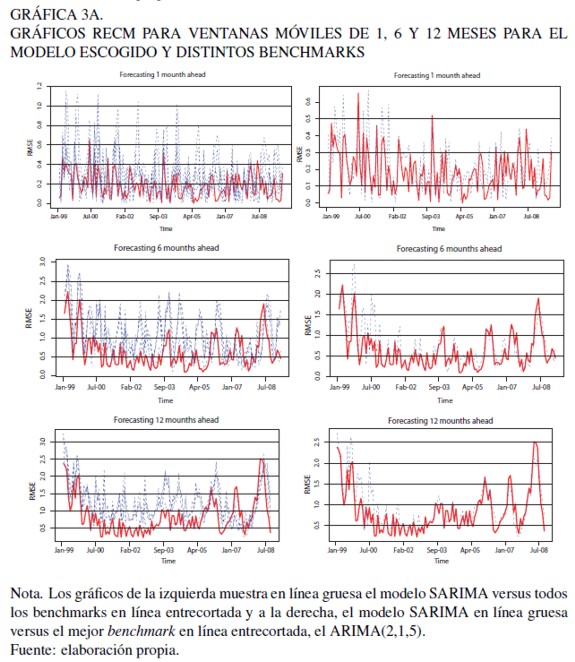
En la Gráfica 3 A de la izquierda, al modelo SARIMA (en línea gruesa) y los benchmarks tradicionales (en línea entrecortada) para los 3 horizontes de predicción; y a la derecha se destaca este segundo mejor modelo (en línea entrecortada) para compararlo con el modelo SARIMA (en línea gruesa), mostrando que a pesar de que los RECM aumentan a medida que crece el horizonte de predicción, los modelos tradicionales no logran superar al modelo SARIMA.
COMENTARIOS FINALES
Según el análisis espectral, se aprecia que los cambios de la tasa de desempleo son netamente cíclicos. Por otra parte, la función de autocorrelación y los métodos de estimación de diferenciación fraccionaria de un modelo ARFIMA permitieron identificar que la variable de interés se comporta como un proceso estacionario. En este contexto, se decidió modelar la tasa de desempleo como un proceso ARIMA(1, 1, 2) × (0, 1, 1)12, según los criterios de información de Akaike, BIC y la función de autocorrelación. Se estableció que la estructura de los modelos de series de tiempo que se analizaron, permite aproximar el período de permanencia de una perturbación en la tasa de desempleo; según el modelo propuesto, la persistencia en la dinámica de la tasa de desempleo podría prolongarse por más de un año.
La evaluación de la capacidad predictiva de los modelos se centra en las proyecciones fuera de muestra de 1, 6 y 12 meses hacia adelante. Los resultados indicaron que la raíz del ECM (RECM) fuera de muestra de las proyecciones SARIMA fue menor que el de los métodos univariados. En particular, el modelo SARIMA permitió realizar proyecciones que son estadísticamente más precisas que las de los benchmarks univariados considerados para todos los horizontes analizados. Por último, si bien no se profundiza en las razones que permiten explicar este comportamiento predictivo, se identifica que éste está asociado a la imposición de dos raíces unitarias en la tasa de desempleo.
NOTAS AL PIE
1 El economista norteamericano Arthur Okun planteó una relación lineal entre los cambios en la tasa de desempleo y las variaciones del producto interno bruto durante la década de 1950. Pese a que la evidencia de tal relación es netamente empírica, es mundialmente reconocida como “una de las regularidades empíricas más confiables de la macroeconomía”.
2 Los datos de desempleo elaborados y publicados por el INE consisten en dividir el número total de personas desocupadas por la fuerza laboral (suma total de personas ocupadas y desocupadas) en el trimestre móvil de cada mes. En otras palabras, la tasa de desempleo mide la proporción de la fuerza laboral que carece de trabajo en el mercado formal.
3 SW (2008), recogen una amplia literatura sobre la habilidad predictiva de la inflación de Estados Unidos entre los procesos univariados de series de tiempo versus los modelos estructurales con variables múltiples. Se considera válido el hallazgo de estos autores desde el punto de vista empírico; principalmente, porque en Chile no hay evidencia reciente de la aplicación de dicho análisis para explicar la tasa de desempleo.
4 Notar que bajo H0, el estadístico tnT es asintóticamente normal.
ANEXOS
ANEXO 1a. MODELO ARFIMA
El término de memoria larga utilizado en el estudio de series de tiempo, suele asociarse con la persistencia que muestran algunas series estacionarias en sus funciones de autocorrelación, que convergen paulatinamente hacia cero. Este comportamiento no es compatible con el modelo SARIMA aquí propuesto, que considera una medida extrema de persistencia de la tasa de desempleo. En este sentido, además del modelo SARIMA, también se ajustó un proceso de larga memoria ARFIMA (Autorregresive Fractionary Integrated Mobile Average) para modelar el comportamiento del desempleo, ya que éste muestra cierta persistencia, lo cual es coherente con el lento ajuste del salario real frente a los distintos estados del ciclo económico. Formalmente se tiene:
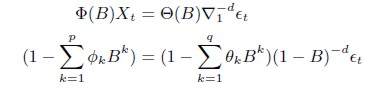 | [8] |
Siendo Φ(B) es un polinomio de coeficientes con operador de rezagos B del componente autorregresivo AR,Θ(B) es el polinomio de coeficientes del proceso de media móvil MA y d corresponde a la diferenciación fraccionaria del modelo. En el Cuadro 1A se presentan tres estimadores para el parámetro d de la tasa de desempleo, en todos los casos se tiene que la serie de tasa de desempleo es no estacionaria.
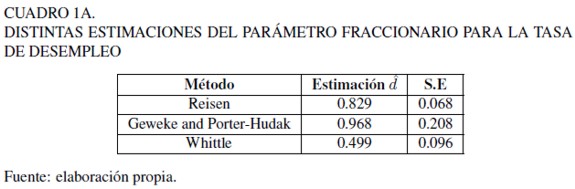
1. Reisen. Basado en la ecuación de regresión usando la función de periodograma alisado como una estimación de la densidad espectral.
2. Geweke y Porter-Hudak. Basado en la ecuación de regresión usando la función de periodograma como una estimación de la densidad espectral.
3. Whittle. Estimador local exacto de Whittle a través del método cuasi-máximo verosímil (ver implementación computacional en Contreras-Reyes et al., 2011).
REFERENCIAS BIBLIOGRÁFICAS
[1] Albagli, E., Contreras, G., García, P., Magendzo, I. y Valdés, R. (2003). Errores de Predicción en Perspectiva. (Documento de Trabajo 199). Santiago de Chile: Banco Central de Chile.
[2] Bergoeing, R., Mornadé, F., Piguillem, F. (2005). Labor Market Distortions, Employment, and Growth: The Recent Chilean Experience. En Chumacero, R.A., Schmidt-Hebbel, K. y Loayza, N. (Ed.). General Equilibrium Models for The Chilean Economy (pp. 395-414). Santiago de Chile: Banco Central de Chile.
[3] Box, G.E.P. y Jenkins, G.M. (1970). Time Series Analysis. Forecasting and Control. San Francisco: Holden-Day.
[4] Brown, R., Durbin, J. y Evans, M. (1975). Techniques for Testing the Constancy of Regression Relationships over Time. Journal of the Royal Statistical Society. Series B (Methodological) 37(2), 149-192.
[5] Contreras-Reyes, J., Goerg, G.M., Palma, W. (2011). afmtools: Estimation, Diagnostic and Forecasting Functions for ARFIMA models. R package version 0.1.1. URL http://cran.r- project.org/web/packages/afmtools/.
[6] Cowan, K., Micco, A., Mizala, A., Pages, C. y Romaguera, P. (2005). Un diagnóstico del desempleo en Chile. Santiago de Chile: Centro de Microdatos, Universidad de Chile.
[7] Christian, J. (2001). Un Modelo de Switching para el Crecimiento en Chile. Cuadernos de Economía, 38(115), 291-319.
[8] Chumacero, R. y Quiroz, J. (1996). La Tasa Natural de Crecimiento de la Economía Chilena: 1985-1996. Cuadernos de Economía, 33(100), 453-72.
[9] Dobre, I. y Alexandru, A. (2008). Modelling Unemployment Rate Using Box Jenkins Procedure. Journal of Applied Quantitative Methods, 3(2), 156-166. Disponible en: http://www.jaqm.ro/issues/volume-3,issue-2/pdfs/dobre_alexandru.pdf
[10] Elliot, G. y Timmerman, A. (2008). Economic Forecasting. Journal of Economic Literature, 46(1), 3-56.
[11] Giacomini, R. y White, H.(2006). Tests of Conditional Predictive Ability. Econometrica, 74(6), 1545-1578.
[12] Geweke, J. y Porter-Hudak, S. (1983). The Estimation and Application of Long Memory Time Series Model. Journal of Time Series Analysis, 4, 221-238.
[13] Gomes, C. y Reis, F. (2009). Measuring Unemployment Persistence of Diferent Labor Force Groups in the Greater Sao Paulo Metropolitan Area. Estudos Econômicos (São Paulo), 39(4), 763-784.
[14] Hylleberg, S., Engle, R., Granger, C. y Yoo, B. (1990). Seasonal integration and cointegration. Journal of Econometrics, 44, 215-238.
[15] Jonathan, D.C. y Kung-Sik, C. (2008). Time Series Analysis With Applications in R, Second Edition. Londres: Springer.
[16] Martínez, C., Morales, G. y Valdés, R. (2001). Cambios estructurales en la demanda por trabajo en Chile. Economía Chilena, 4(2), 5-25.
[17] Newey, W.K. y West, K.D. (1987). A Simple, Positive Semidefinite, Heteroskedasticity and Auto-correlation Consistent Covariance Matrix. Econometrica, 55(3) 703-708.
[18] Pincheira, P. y García, A. (2009). Forecasting Inflation in Chile With an Accurate Benchmark (Working Papers, Central Bank of Chile 514). Santiago de Chile: Banco Central de Chile.
[19] R Development Core Team (2011). R: A Language and Environment for Statistical Computing. Viena: R Foundation for Statistical Computing. http://www.R-project.org.
[20] Reisen, V.A. (1994). Estimation of the Fractional Diference Parameter in the ARFIMA(p,d,q) model using the Smoothed Periodogram. Journal of Time Series Analysis, 15(3), 335-350.
[21] Rodríguez, J. (2007). Desempleo en Chile 1998-2007: Shocks Productivos o Distorsiones en el Mercado Laboral? (Tesis inédita de maestría). Universidad de Chile, Santiago de Chile, Chile.
[22] Stock, J.H. y Watson, M.W. (2003). Forecasting Output and Inflation: The Role of Asset Prices. Journal of Economic Literature, 41(3), 788-829.
[23] Stock, J.H. yWatson, M.W. (2006). Why Has U.S. Inflation Become Harder to Forecast? (NBER Working Papers 12324). Cambridge: National Bureau of Economic Research.
[24] Stock, J.H. y Watson, M.W. (2008). Phillips Curve Inflation Forecasts (NBERWork-ing Papers 14322). Cambridge: National Bureau of Economic Research.
[25] Whittle P. (1962). Gaussian estimation in stationary time series. Bulletin of the International Institute of Statistics, 39, 105-129.