LA DEMANDA AGREGADA Y LA DISTRIBUCIÓN DEL INGRESO: UN ESTUDIO A PARTIR DE LOS MODELOS DE CRECIMIENTO KALECKIANOS
Osmar Leandro Loaiza Quintero1
1 Economista y estudiante de maestría en Ciencias Económicas. Se desempeña como docente de la Universidad Nacional de Colombia, sede Medellín. E-mail: olloaizaq@unal.edu.co. Dirección de correspondencia: Calle 66C, 37-33. Apto 301, Medellín 050012, Colombia.
El autor agradece al profesor Alexander Tobón, del Departamento de Economía de la Universidad de Antioquia, por sus valiosos comentarios en la elaboración de este trabajo.
Este artículo fue recibido el 3 de mayo de 2011, la nueva versión el 24 de enero de 2012 y su publicación aprobada el 11 de marzo de 2011.
Resumen
un estudio a partir de los modelos de crecimiento kaleckianos. Cuadernos de Economía, 31(58), 23-47. El objetivo del presente artículo es analizar los mecanismos por medio de los cuales la demanda agregada y la distribución del ingreso determinan la tasa de crecimiento, en el marco de la teoría poskeynesiana inspirada por Michael Kalecki, contrariamente a lo que sugiere la teoría neoclásica, en la que el crecimiento solo depende de los factores asociados a la oferta. El rechazo de la ley de Say, sugerido por este tipo de modelos, permite mostrar el impacto que tiene la demanda sobre la tasa de crecimiento, dependiendo de la sensibilidad de las decisiones de ahorro e inversión ante modificaciones en el ingreso tanto de los trabajadores como de los capitalistas.
Palabras clave: crecimiento económico, demanda, teoría neoclásica, teoría poskeynesiana, ley de Say, distribución del ingreso.
JEL: E22, O10, O15.
Abstract
The aim of this paper is to study the mechanisms through which aggregate demand and income distribution affect the rate of growth, in a post-Keynesian framework rooted in the works of Michal Kalecki. Thus, this paper addresses some issues that are put aside by neoclassical theory, which focuses on supply side phenomena to explain growth. The Say's law refusal implied by the framework employed allows the reader to determine the influence that demand exerts on economic growth, which also depends upon the sensibility of saving and investment decisions to changes in the income shares of workers and capitalists.
Keywords: economic growth, demand, neoclassical theory, post-Keynesian theory, Say's law, income distribution.
JEL: E22, O10, O15.
Resumè
Le but de cet article est d'analyser les mécanismes par lesquels la demande globale et la distribution des revenus déterminent le taux de croissance, dans le cadre de la théorie postkeynésienne inspirée par Michael Kalecki, contrairement à ce qui suggère la théorie néoclassique, dans laquelle la croissance ne dépend que des facteurs de croissance associés à l'offre. Le rejet de la loi de Say, suggéré par ce type de modèles, permet de montrer l'impact qui a la demande sur le taux de croissance, en dépendant de la sensibilité des décisions d'épargne et d'inversion vis-À-vis les modifications dans les revenus des travailleurs et des capitalistes.
Mots clés : croissance économique, demande, théorie néoclassique, théorie postkeynésienne, loi de Say, distribution de revenus.
JEL: E22, O10, O15.
El modelo de referencia para la teoría neoclásica del crecimiento es el propuesto por Solow (1956). Este ha servido de base para la elaboración de otros modelos en esa tradición, los cuales han permitido el refinamiento en las explicaciones sobre la acumulación de capital. En efecto, basta con agregar o modificar algún supuesto en el modelo de Solow para obtener, por ejemplo, el de Ramsey-Cass-Koopmans2 o los modelos de crecimiento endógeno. A pesar de las divergencias que pueden presentar en torno a sus supuestos y resultados, estos modelos comparten ciertos rasgos. En primer lugar, atribuyen a los determinantes de la oferta la explicación de la tasa de acumulación de capital y, por tanto, del crecimiento de una economía; en segundo lugar, omiten el estudio de los canales por medio de los cuales la distribución del ingreso entre salarios y beneficios puede afectar el crecimiento.
El énfasis en los factores de oferta se explica esencialmente por el respeto de la ley de Say, no solo en los modelos de crecimiento sino, en general, en toda la macroeconomía neoclásica. De acuerdo a la ley de Say, la oferta crea su propia demanda, es decir que cualquier incremento de la oferta crea el poder de compra (o genera el ingreso) necesario para poder adquirir la nueva producción, garantizando la igualdad entre la oferta y la demanda, y, por lo tanto, el mantenimiento de la hipótesis de pleno empleo. La identidad entre el ahorro y la inversión resulta ser un corolario de esta ley (como lo señala Keynes, 1954, p. 19), pues implica que aquella parte del ingreso que no se consume se traduce en demanda destinada a satisfacer las necesidades de acumulación o, lo que es lo mismo, en inversión. Pero si la demanda sigue o se acomoda al comportamiento de la oferta, conservando el equilibrio macroeconómico, no tiene caso analizar en profundidad el impacto de la demanda sobre el crecimiento, razón por la cual esta ocupa un papel despreciable, a pesar de que es posible relacionarla con el proceso de acumulación (como en el modelo de Ramsey-Cass-Koopmans).
En este sentido, por ejemplo, el modelo de Solow en su forma básica considera la tasa de ahorro exógena y, en consecuencia, ignora las decisiones de consumo de los individuos que dan lugar a esa tasa de ahorro. Aunque el modelo de Ramsey-Cass- Koopmans endogeniza la tasa de ahorro, al considerar explícitamente el problema de maximización intertemporal al que se enfrentan los individuos en la decisión sobre su consumo presente y futuro, se obtiene que, sin importar el nivel de la tasa de ahorro -y, por tanto, del consumo-, la tasa de crecimiento es cero en el largo plazo, tal como ocurre en el modelo Solow. Esto implica que la demanda no juega ningún papel en la explicación del crecimiento.
De hecho, si la tasa de crecimiento de largo plazo es positiva, esto se explicaría por el comportamiento de los determinantes exógenos de la oferta, tales como el progreso técnico, la tasa de crecimiento de la fuerza laboral o por las condiciones técnicas de producción (como los rendimientos de escala o las externalidades en los modelos de crecimiento endógeno). Pero es cuestionable que tanto Ramsey- Cass-Koopmans como Solow enfaticen en la determinación de un equilibrio sin crecimiento en el largo plazo y que, una vez alcanzado este equilibrio, el crecimiento reaparezca como resultado de la introducción de fenómenos que no surgen al interior del modelo; lo que equivale a admitir que teóricamente una economía no es capaz en el largo plazo de asegurar su propia expansión.
Por otra parte, el aparente desinterés de la teoría neoclásica por estudiar temas relacionados con la distribución del ingreso en el ámbito de la economía positiva se debe a que, adhiriendo a John Stuart Mill, considera que el análisis de tal tipo de problemas hace propensa a la teoría a contaminarse con sesgos de tipo ideológico o subjetivo. Sin embargo, el estudio de la distribución del ingreso y su relación con la acumulación de capital ha ocupado un lugar central en el desarrollo de la ciencia económica.
Este era precisamente uno de los temas de indagación de los economistas clásicos como Smith, Malthus y Ricardo; este último incluso defendía que determinar las leyes que regulan la distribución del producto entre las diferentes clases sociales era el principal problema de estudio de la economía. Además, en años recientes se han publicado diversos estudios empíricos en el marco de la teoría poskeynesiana que demuestran la relevancia de este tema, como los de Hein y Vogel (2008), Hein y Tarassow (2008) y Stockhamer et al. (2009), entre otros, en los cuales se estima para varios países el efecto de la distribución del ingreso entre salarios y beneficios sobre la tasa de crecimiento y se encuentra evidencia que muestra que dicho efecto es lo suficientemente importante como para ser ignorado.
Así pues, las limitaciones que presentan los modelos neoclásicos de crecimiento hacen pertinente adoptar un enfoque teórico alternativo en el cual no se recurra a la ley de Say. En particular, esto permite evaluar con mayor precisión la influencia de la demanda sobre el proceso de crecimiento económico, en tanto esta deja de ser un agregado que sigue pasivamente el comportamiento de la oferta. Los modelos de crecimiento kaleckiano inscritos en la tradición poskeynesiana, ofrecen las herramientas teóricas necesarias para efectuar tal análisis y permiten, igualmente, llamar la atención sobre la importancia que tiene la distribución del ingreso en la explicación del crecimiento. Por lo tanto, el objetivo de este trabajo es analizar los canales por medio de los cuales la demanda y la distribución del ingreso afectan la tasa de crecimiento, a través del examen teórico del enfoque kaleckiano.
En la primera sección se exponen algunos rasgos clave de la teoría poskeynesiana, que sirven de fondo teórico para los modelos de crecimiento kaleckiano. Esto permitirá al lector entender algunas de las diferencias de estos modelos con respecto a los que siguen un enfoque neoclásico y obtener una mejor comprensión del modelo de crecimiento kaleckiano que se expondrá en la segunda sección. En la tercera sección se propone una generalización de este modelo con base en el marco teórico ofrecido por Bhaduri y Marglin (1990). Finalmente, se ofrecen algunas conclusiones.
ELEMENTOS PARA UNA TEORÍA DEL CRECIMIENTO KALECKIANA
Aunque la Teoría General de Keynes es usualmente considerada la fuente de inspiración de la teoría poskeynesiana, es el trabajo deMichal Kalecki el que determina gran parte de las características esenciales de esta teoría, entre las cuales se destaca el interés por relacionar el crecimiento con la distribución del ingreso entre las distintas clases sociales. Tradicionalmente estas clases se diferencian por su relación con respecto a los medios de producción o capital: por un lado están los capitalistas, que poseen el capital y son propietarios de las firmas, y cuyos ingresos corresponden a los beneficios (R) obtenidos por el uso del capital; por otro lado, están los trabajadores desprovistos de capital, quienes derivan su ingreso (W) de la venta de su fuerza de trabajo. De acuerdo con lo anterior, el ingreso nacional (Y ) es:
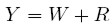 | [1] |
Dicho ingreso se destina a la inversión (I) y al consumo (C), el cual se compone por el consumo de los trabajadores (Cw) y de los capitalistas (Cc):
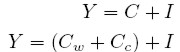 | [2] |
Los capitalistas, en su calidad de propietarios de las firmas, están interesados en retener una parte de sus beneficios para financiar las nuevas inversiones y garantizar así la reproducción y la expansión de sus empresas (Stockhmmer, 1999, p. 5). Del mismo modo, es posible suponer que los trabajadores también ahorran una parte de sus salarios con el fin de acceder al consumo futuro. Sin embargo, dado que el ahorro de los capitalistas se traduce en inversión y el ahorro de los trabajadores en consumo futuro, es perfectamente admisible suponer que la propensión marginal a ahorrar de los trabajadores (sw) es menor que la de los capitalistas (sc). Esta hipótesis equivale a asumir que los trabajadores consumen una proporción (cw) de su ingresomás alta que los capitalistas. Sin embargo, con el propósito de simplificar la exposición, suponemos que los trabajadores no ahorran o, lo que es lo mismo, que su propensión marginal a consumir es uno (cw = 1), lo que implica que los trabajadores consumen todo su ingreso (Cw = W). En este caso, la función de ahorro agregado (S) solo depende de las decisiones de los capitalistas2.
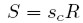 | [3] |
La ecuación (2) ahora puede escribirse como sigue:
 |
Despejando en (1) para W, la anterior ecuación se puede reescribir así:
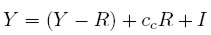 |
Reordenando esta última, se obtiene la siguiente expresión para los beneficios:
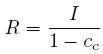 | [4] |
Esta expresión es interesante porque muestra que los capitalistas no pueden decidir directamente cuánto ganar, pero sí pueden decidir cuánto invertir y cuánto consumir, de manera que son "sus decisiones de inversión y consumo las que determinan las ganancias, y no a la inversa" (Kalecki, 1982, p. 95). Así, en el agregado es el gasto de los capitalistas lo que determina sus beneficios. Si se divide la expresión (4) por el stock de capital K, se obtiene una expresión fundamental para la teoría poskyenesiana: la ecuación de Cambridge, la cual relaciona la tasa de beneficio, definida como r = R / K , con la tasa de crecimiento o acumulación, definida como g = I / K:
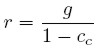 | [5] |
La ecuación de Cambridge muestra que una mayor inclinación al consumo por parte de los capitalistas no solo incrementa la masa de los beneficios, sino que también se traduce en una tasa de beneficio más alta. Asimismo, se observa que la tasa de beneficio solo es positiva si la tasa de crecimiento también es positiva. Por tanto, un equilibrio de estado estacionario en el cual la economía no crece (gt−1 = gt = g* = 0) solo puede ocurrir cuando no se obtienen beneficios, lo cual es una situación indeseable para los capitalistas, en la que no hay ningún incentivo para comprometerse con nuevas inversiones.
En el enfoque poskeynesiano de los modelos kaleckianos, la distribución de los ingresos juega un rol esencial, razón por la cual es necesario establecer algún tipo de medida. Para tal efecto, se emplea como variable indicadora de la distribución de ingresos el cociente h = R / Y , que representa la proporción de los beneficios en el ingreso nacional y cuyo recíproco (1 − h) representa la proporción de los salarios en el ingreso nacional. Ahora, dividiendo en (4) por Y y reordenando los términos, se obtiene que:
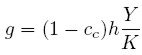 | [6] |
De acuerdo con la ecuación (6), dada la productividad media del capital 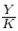 , entre
mayor sea la parte del ingreso nacional correspondiente a los beneficios h y, por tanto, menor la parte que está destinada a los trabajadores (1 − h) en forma de salarios, mayor será la tasa de crecimiento g. En consecuencia, la ecuación (6) ilustra la relación existente entre la distribución del ingreso, representada por h, y la acumulación de capital representada por la tasa de crecimiento g.
, entre
mayor sea la parte del ingreso nacional correspondiente a los beneficios h y, por tanto, menor la parte que está destinada a los trabajadores (1 − h) en forma de salarios, mayor será la tasa de crecimiento g. En consecuencia, la ecuación (6) ilustra la relación existente entre la distribución del ingreso, representada por h, y la acumulación de capital representada por la tasa de crecimiento g.
Asimismo, la consideración del problema de la distribución sirve como eslabón para relacionar los precios monetarios con el crecimiento, es decir, permite mostrar que el papel de los precios no se limita a la asignación de recursos, ya que un cambio en los precios también tiene un impacto sobre la distribución del ingreso y, por esta vía, sobre el crecimiento económico. Siguiendo de nuevo a Kalecki, se adopta un escenario de competencia monopolística en el cual existen reservas de capacidad productiva y en el que las firmas fijan el precio unitario del bien producido (P) de acuerdo a un mark-up (m) sobre el costo marginal (z):
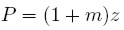 | [7] |
Por un lado, el mark-up es estrictamente positivo y está determinado esencialmente por dos factores exógenos relacionados con la oferta. El primero tiene que ver con el grado de monopolio, pues refleja la intensidad de la competencia entre las firmas; así, entre menor sea la competencia más alto será el mark-up. El segundo factor tiene que ver con el estado de la lucha de clases, esto es, la puja entre capitalistas y trabajadores por una apropiación mayor del ingreso nacional, la cual se refleja en la capacidad de los trabajadores para negociar mayores salarios. Un mayor poder de negociación de los trabajadores se traduce en un menor mark-up, debido a que reduce la capacidad del empresario para contrarrestar un incremento dado en el salario nominal con incrementos equivalentes en los precios.
Por otro lado, el costo marginal establece una relación directa con las condiciones de producción. Las firmas tienden a conservar reservas en su capacidad productiva, esencialmente por razones estratégicas o simplemente como precaución ante cambios imprevistos en la demanda (Kalecki, 1982, p. 57). Mientras se produzca por debajo de la capacidad máxima el costo marginal (z) es constante y, por tanto, igual al costo medio. Asimismo, la productividad marginal del trabajo definida como yl también es constante e igual a la productividad media.
Esta teoría de la determinación de los precios monetarios permite entonces establecer una relación con la capacidad instalada. El grado de utilización de la capacidad instalada se mide por medio del coeficiente de utilización (u) definido como el cociente entre el producto efectivo y el producto potencial 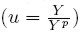 . Sea w el salario real, que en una economía sin Gobierno es igual al costo real de una unidad de trabajo pagado por los capitalistas. El costo marginal se puede expresar como:
. Sea w el salario real, que en una economía sin Gobierno es igual al costo real de una unidad de trabajo pagado por los capitalistas. El costo marginal se puede expresar como:
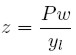 | [8] |
Reemplazando (8) en (7) y despejando para w:
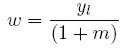 | [9] |
Esta expresión ilustra que por debajo de la plena capacidad (u < 1) el salario no depende de factores de demanda, sino de las condiciones de oferta, reflejadas en (9) por la productividadmarginal del trabajo (yl) y por el mark-up sobre los costos (m). Asimismo, los precios también son determinados por la condiciones de oferta, pues dependen del mark-up y del costo marginal, que a su vez está en función de la productividad del trabajo. Por tanto, bajo estas condiciones un cambio en la demanda no afectaría los precios ni el salario real, pues dicho cambio sería enfrentado a través de un ajuste en los niveles de utilización de la capacidad instalada y, por tanto, se reflejaría enteramente en un cambio en el nivel de producción. Sin embargo, cuando se alcanza la plena capacidad, esto es, cuando u = 1, entonces:
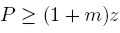 | [7a] |
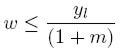 | [9a] |
Estas dos últimas expresiones ilustran que cuando las empresas trabajan a plena capacidad ya no pueden responder modificando su nivel de producción, por lo que cualquier incremento de la demanda eleva los precios y, como resultado, reduce los salarios reales.
Para completar los elementos fundamentales que constituyen el enfoque kaleckiano, es necesario introducir la distribución de ingresos. El agregado de los salarios (W) está determinado por el producto entre el número total de trabajadores empleados y el salario real (w):
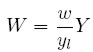 |
Recordando la definición de h, y teniendo en cuenta que P / P = 1 y que R = Y −W:
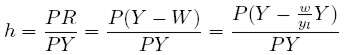 |
Reemplazando (8) y (7) en la anterior expresión se tiene:
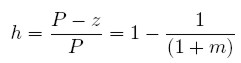 | [10] |
Esta ecuación muestra la relación que existe entre los precios y la distribución. Entre más alta sea la diferencia entre el precio y el costo de una unidad producida, es decir, entre mayor sea el mark-up, mayor será el volumen de los beneficios con respecto al ingreso nacional y menor la parte correspondiente a los salarios. Recordando que la distribución está relacionada con la tasa de crecimiento, tal como lo muestra la ecuación ( 6), se hace visible que, a través de su impacto sobre la distribución, las variaciones en los precios pueden tener importantes efectos sobre el crecimiento, lo cual muestra que el papel de los precios no se limita al problema de la asignación de recursos. En efecto, para los modelos de crecimiento kaleckiano los precios son importantes no tanto por su papel como determinantes de la demanda, sino por su relación con la distribución del ingreso.
UN MODELO BÁSICO DE CRECIMIENTO KALECKIANO
Una vez presentados los elementos constitutivos de una teoría del crecimiento en el enfoque kaleckiano, procedemos a exponer un sencillo modelo basado en Amadeo (1986). Supongamos una economía real, cerrada y sin Gobierno, para la cual la función de inversión representa la demanda agregada, mientras que la función de ahorro -como en (3)- representa la oferta agregada. Bajo esta simple estructura, el interés de los modelos de crecimiento kaleckiano consiste en determinar la tasa de crecimiento de estado estable (gt−1 = gt = g* > 0), esto es, la tasa de crecimiento tendencial o de largo plazo y los factores que la explican. El estado estable se alcanza cuando se verifica el equilibrio entre la oferta y la demanda globales. Es necesario enfatizar que aquí la igualdad entre el ahorro y la inversión solo es una condición de equilibrio y no una identidad, lo que implica el rechazo de la ley de Say e inscribe este modelo en la tradición poskeynesiana.
La determinación de la tasa de crecimiento de equilibrio
La tasa de crecimiento de equilibrio depende de una relación precisa entre el ahorro y la inversión. Aunque los modelos en la tradición kaleckiana con frecuencia difieren en la forma particular que toma la función de inversión, ellos coinciden en que debe estar relacionada positivamente con el coeficiente de utilización (u). En concreto, se espera que cuando las firmas observan un aumento en los niveles de utilización de la capacidad instalada, como resultado de un incremento en la producción para afrontar una mayor demanda, se vean incentivadas a incrementar su gasto en inversión. Este gasto se destina a incrementar la capacidad productiva, en vista de nuevos incrementos en la producción o por consideraciones estratégicas como, por ejemplo, preservar cierta capacidad ociosa que permita enfrentar incrementos imprevistos en la demanda o disuadir la entrada de nuevos competidores. Por tanto, la siguiente función de inversión constituye una buena aproximación para ilustrar de manera precisa y simple la estructura y los principales resultados de los modelos de crecimiento kaleckiano:
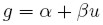 | [11] |
Donde α, β son constantes positivas. Por otra parte, la función de ahorro está dada por la expresión (3); sin embargo, es conveniente reescribirla dividiendo por el stock de capital K:
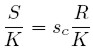 |
Multiplicando por 1 = Yp /Yp y por 1 = Y/Y se tiene:
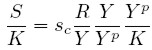 |
Definiendo σ = S/K como la razón ahorro-capital, u = Y/Yp como el coeficiente de utilización y v = K/Yp como la razón capital-producto potencial, entonces la función de ahorro se puede escribir como sigue:
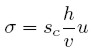 | [12] |
Recordando que el equilibrio, el cual determina la tasa de crecimiento de estado estable, se define por la igualdad entre el ahorro y la inversión:
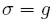 | [13] |
Entonces, reemplazando (11) y (12):
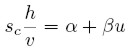 | [13a] |
La Gráfica 1 ilustra los resultados del modelo. El equilibrio definido en (13a) se representa por la intersección de la curva de ahorro, σ0, con la curva de inversión, g, en el punto E1, al cual corresponde la tasa de crecimiento de estado estable g*1 -medida en el eje vertical- y el coeficiente de utilización u*1 -medido en el eje horizontal-.
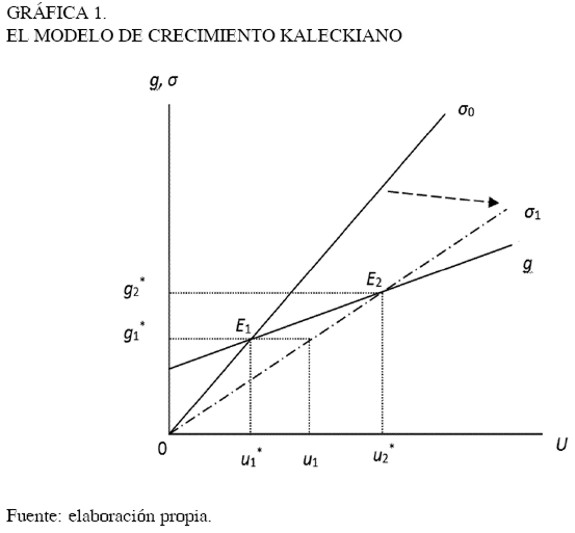
Ahora bien, para que el equilibrio E1 sea estable, el ahorro debe ser más sensible que la inversión ante variaciones en las cantidades, las cuales, en el marco del presente modelo, se reflejan enteramente en variaciones en el coeficiente de utilización. Esto garantiza que, ante cambios en la demanda, la oferta se ajuste rápidamente para eliminar el desequilibrio. En consecuencia, la condición de estabilidad es:
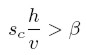 | [14] |
Como se muestra en la Gráfica 1, lo anterior implica que la pendiente de la curva de ahorro, σ0, es mayor que la pendiente de la curva de inversión, g.
Dada la condición de estabilidad (14 ), si la economía se encuentra en un punto a la izquierda de E1, en el cual la inversión es mayor que el ahorro (g > σ0), de manera que hay un exceso de demanda, las firmas responden incrementando la producción hasta que se satisfaga esa demanda excedentaria. Asimismo, si hay un exceso de oferta (g < σ0 ), de modo que la economía se encuentra en un punto a la derecha E1, los oferentes responden recortando su producción, eliminando el desequilibrio. Si no se cumple la condición de estabilidad, la curva de inversión tendría una pendiente igual o mayor que la curva de ahorro. Esto implicaría, entonces, que, ante un cambio en la demanda, la oferta no se ajustaría con la suficiente rapidez como para eliminar el desequilibrio resultante.
Como se desprende del anterior análisis, cualquier punto diferente al lugar de la intersección de las curvas de ahorro e inversión, que corresponde al punto E1, es un desequilibrio. Esto implica, en consecuencia, que la trayectoria de ajuste desde cualquier punto en la Gráfica 1 hacia el punto E1 es una sucesión de desequilibrios. En otras palabras, en el corto y mediano plazo el sistema económico está en desequilibrio. Este solo desaparece en el muy largo plazo, cuando todas las variables se han ajustado lo suficiente como para permitir el equilibrio entre el ahorro y la inversión, punto en el cual los empresarios no encuentran incentivo alguno para modificar sus decisiones de inversión, pues la tasa de crecimiento de la demanda y la oferta son iguales y positivas y, por tanto, todo lo que se produce se vende. Esta situación es muy diferente a la que se encuentra en los modelos de crecimiento neoclásicos, en los cuales la economía siempre está en equilibrio, es decir, tanto en largo como en el corto plazo se verifica la igualdad entre el ahorro y la inversión, debido a la hipótesis de la ley de Say.
Estática comparativa
Con el fin de explicar dos resultados importantes de este modelo de crecimiento kaleckiano, se efectuará un análisis de estática comparativa. El primer caso paradoja del ahorro) permitirá entender la importancia de la demanda en la determinación de la tasa de crecimiento de equilibrio, e ilustra las consecuencias de abandonar la hipótesis de la ley de Say. El segundo caso (la paradoja de los costos) permite analizar cómo la distribución del ingreso, a través de su impacto sobre la demanda, afecta el crecimiento.
La paradoja del ahorro
Supóngase que hay una disminución en la propensión marginal a ahorrar de los capitalistas (sc). De acuerdo a la ecuación (12), es evidente que esto se traduce en una disminución en la pendiente de la curva de ahorro, la cual pasa de σ0 a σ1 en la Gráfica 1. Dicha reducción en el ahorro implica un aumento en el consumo que eleva la demanda agregada, lo cual incita a los empresarios a incrementar la producción. De esta manera, en el corto plazo, a la tasa de acumulación inicial g*1 corresponde un nivel de utilización mayor, igual a u1, como se muestra en la Gráfica 1.
En virtud de (11), es visible que un aumento en el nivel de utilización tiene un impacto positivo sobre la inversión, dado que el mayor volumen de la demanda y la producción hace que las empresas anticipen niveles de utilización de la capacidad instalada más altos. Esto las induce a incrementar el gasto de inversión, el cual provoca a su vez un nuevo incremento en la demanda agregada. En consecuencia, se presentan nuevos incrementos de la producción y del nivel de utilización de la capacidad, que elevan la tasa de crecimiento. Este proceso de retroalimentación continúa hasta que la oferta alcanza la demanda, estos es, hasta que se llega al equilibrio E2, con tasa de crecimiento (o de acumulación) g*2 y coeficiente de utilización u*2.
Este caso se corresponde con la paradoja del ahorro de Keynes, debido a que la disminución inicial en la propensión marginal a ahorrar de los capitalistas permite obtener en el largo plazo una tasa de crecimiento y un grado de utilización más elevados. Además, a partir de (5) es evidente que la tasa de beneficio de largo plazo es también más alta. Este resultado es interesante porque muestra que para lograr mayores tasas de crecimiento no es necesario incrementar el nivel de ahorro corriente, como lo implicaría la identidad entre el ahorro y la inversión. Si se rechaza esta identidad, es decir, si se rechaza la ley de Say, es posible estudiar la inversión como una variable diferente del ahorro y, por tanto, como una variable que responde a unos determinantes diferentes.
Si se considera que el nivel de inversión deseado por las firmas depende de sus expectativas de rentabilidad o de crecimiento en las ventas, ellas pueden estar dispuestas a ejecutar niveles de inversión que superen el nivel de ahorro corriente, con la expectativa de que los retornos futuros generen una fuente de ingresos suficiente como para obtener el nivel de ahorro requerido para cubrir los gastos incurridos en el pasado. En otras palabras, es la producción la que precede al ingreso, y no al contrario -como se deduce de la ley de Say-. De acuerdo a la condición de equilibrio (13), es entonces claro que la economía no solo obtiene mayores tasas de crecimiento en el largo plazo como consecuencia del incremento inicial en la demanda, sino también un nivel de ahorro mayor. De esta manera, altas tasas de ahorro son posibles gracias a altos niveles de inversión, pues la inversión genera el ahorro.
La paradoja de los costos
Otro resultado importante se obtiene cuando se consideran los efectos de un incremento en el salario real (w) debido a una disminución en el mark-up, la cual puede ser consecuencia de una intensificación de la competencia, que causa una disminución en el nivel de precios, o de un mayor poder de negociación por parte de los trabajadores, que impide a los empresarios transferir un incremento en el salario nominal a los precios. La ecuación (10) muestra que una disminución en m causa una reducción de h. Por lo tanto, dado el nivel de ingreso nacional, un incremento salarial -debido a una disminución en m- implica una redistribución de los beneficios hacia los salarios, que se refleja en una disminución de la proporción de los beneficios sobre el producto (h) y se traduce en una reducción de la pendiente de la curva de ahorro, representada ahora por σ1, como se muestra en la Gráfica 1. Para analizar el efecto sobre la tasa de beneficio (r = R/K), se efectúa la siguiente manipulación:
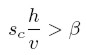 |
La cual permite expresar la tasa de beneficio en función de h y u:
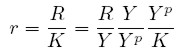 | [15] |
Si el coeficiente de utilización es constante, una disminución en la proporción de los beneficios sobre el producto (h) significaría una menor tasa de beneficio. Ahora bien, en los modelos de crecimiento en la tradición kaleckiana, siempre que existan reservas de capacidad productiva, el coeficiente de utilización puede variar, razón por la cual un incremento salarial no necesariamente se traduce en una reducción en la tasa de beneficios. De hecho, como los trabajadores gastan una proporción mayor de su ingreso que los capitalistas, un aumento en los salarios reales genera un incremento en el consumo y, en consecuencia, un aumento en la demanda agregada.
Como resultado se produce un incremento en las ventas que aumenta el grado de utilización, el cual, en el corto plazo (es decir, dado g*1), pasa de u1* a u1, contrarrestando el efecto negativo de la disminución de h sobre la tasa de beneficio, de manera que esta no disminuye. Por el contrario, el mayor nivel de demanda incita a los empresarios a elevar el gasto de inversión, de modo que la tasa de crecimiento aumenta hasta que se elimina la brecha entre la oferta agregada y la demanda agregada provocada por el incremento salarial. De esta forma, el aumento de la demanda agregada resultante de la redistribución del ingreso hacia los trabajadores permite que la economía alcance un equilibrio de estado estable superior en el punto E2, con una tasa de crecimiento y un coeficiente de utilización más altos, como se observa en la Gráfica 1.
Igualmente, de acuerdo a la ecuación (5 ), es obvio que en el nuevo equilibrio la tasa de beneficio es mayor, debido a que la propensión a ahorrar de los capitalistas permanece constante, pero la tasa de acumulación es más alta que antes. Esta es la paradoja kaleckiana de los costos: el aumento de los costos provocado por el incremento salarial, en lugar de tener un impacto negativo sobre la producción y los beneficios, condujo a un aumento en la tasa de beneficio y en la tasa de crecimiento.
Este resultado revela lo que sería un error de agregación en la teoría neoclásica: cada empresa tomada individualmente lograría aumentar sus beneficios si reduce sus costos laborales, en especial mediante una reducción de los salarios. Pero si esta reducción de los salarios es generalizada, mientras el conjunto de las empresas mantiene su margen de beneficios y los precios a un nivel fijo, se venderían menos productos y no por ello aumentarían sus beneficios (Lavoie, 2005, p. 100). Por tanto, "lo que es ventajoso para un empresario aislado no lo es necesariamente para el conjunto de los empresarios considerados como clase" (Kalecki, 1982, p. 26). Para ponerlo en términos más generales, el comportamiento del agregado no necesariamente replica el comportamiento del agente individual.
UNA EXTENSIÓN DEL MODELO DE CRECIMIENTO KALECKIANO
De acuerdo con la paradoja de los costos, un incremento del salario real tiene un efecto positivo sobre la tasa de crecimiento. Este resultado del modelo de crecimiento kaleckiano se explica por la forma particular de la función de inversión (11), la cual solo recoge los efectos positivos de un incremento salarial reflejados en un incremento del consumo, que conducen a un alza del grado de utilización de la capacidad instalada. Sin embargo, un aumento salarial también tiene un efecto negativo sobre la oferta, en tanto implica un aumento en los costos variables de producción. Ahora bien, esto complica el análisis porque significa que una variación en los salarios tiene efectos opuestos que hacen difícil determinar su impacto sobre el crecimiento y la inversión.
Dentro de la tradición kaleckiana, Bhaduri y Marglin (1990) exponen un modelo macroeconómico que estudia la relación entre los salarios y el nivel de utilización en el corto plazo, en el cual esos efectos opuestos son explícitamente considerados. Teniendo como referencia este modelo, presentamos un modelo en el cual es posible analizar también los determinantes de la tasa de crecimiento, incorporando los efectos opuestos de una variación de los salarios. Con tal propósito, se propone modificar la función de inversión como sigue:
g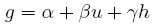 | [11a] |
Donde α, β y γ son parámetros positivos. Al igual que en el modelo de crecimiento kaleckiano, esta función depende positivamente del coeficiente de utilización (u). La diferencia radica en la inclusión de la variable h, la proporción de los beneficios sobre el ingreso nacional. Esta variable refleja la situación de costos para las empresas, en tanto cualquier incremento (disminución) en los costos de producción se traduce en una reducción (aumento) en el margen de beneficios por cada unidad producida, lo cual, de acuerdo a la ecuación (10), se refleja necesariamente en una disminución (aumento) de h. Por tanto, la función de inversión en (11a) ofrece la ventaja de separar los impactos de demanda reflejados por u, de los impactos de oferta reflejados por h (Bhaduri y Marglin, 1990, p. 380). Además, permite considerar de manera explícita y directa los efectos de la distribución del ingreso.
Dado que es la inclusión de la variable h, en la función de inversión, la diferencia clave entre el modelo que se desarrollará a continuación y el modelo de crecimiento kaleckiano, en lo que sigue se investiga cómo las variaciones en h afectan la demanda y la tasa de crecimiento. Con tal propósito, a continuación se determina el equilibrio.
La determinación de la tasa de crecimiento de equilibrio
La función de ahorro es la misma que la dada en (12). Por lo tanto, de acuerdo a (13) el equilibrio está dado por la igualdad entre las ecuaciones (11a) y (12):
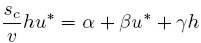 | [13a] |
Antes de estudiar el comportamiento de la tasa de crecimiento y la manera como es afectada por variaciones en h, conviene determinar cómo varía en el equilibrio el nivel de utilización u* cuando cambia la distribución del ingreso, reflejada por h. Para ello, se deriva en (13c) con respecto a h.
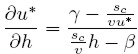 | [16] |
La estabilidad del equilibrio requiere que la oferta responda de manera más elástica que la demanda ante variaciones en el coeficiente de utilización. En consecuencia, la condición de estabilidad dada por la expresión (14) también es válida en el presente modelo. Esta condición implica que el denominador en (16) es positivo. Por tanto, el signo de esta expresión depende del numerador, esto es, de la respuesta relativa de la inversión el ahorro ante un cambio en h. Así, podemos distinguir dos casos:
1. Si γ < (sc/v)u*, entonces la inversión es menos sensible que el ahorro frente a un cambio en la proporción de los beneficios sobre el producto agregado. En ese caso, una disminución del salario real provoca una caída en el consumo que no es compensada por el aumento de la inversión, dado el incremento en h. En consecuencia, la demanda agregada (C + I) disminuye, llevando a las empresas a reducir el nivel de producción, lo que resulta en una relación negativa entre u y h.
2. En contraste, si la inversión es más sensible que el ahorro ante un cambio en h, esto es, si γ > (sc/v)u*, entonces una caída en el consumo provocada por una disminución en el salario real es más que contrarrestada por el aumento en la inversión debido al correspondiente aumento en h, por lo que la demanda agregada aumenta, elevando el nivel de utilización u (Bhaduri y Marglin, 1990, p. 381).
A continuación se analiza cómo varía la tasa de crecimiento en el equilibrio g* ante variaciones en h. La tasa de crecimiento de equilibrio es:
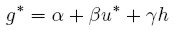 | [11b] |
De manera que derivando g* con respecto a h:
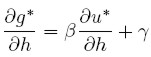 |
Reemplazando (16):
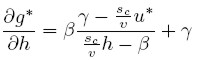 |
Y reordenando términos:
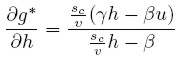 | [17] |
Igualmente, la condición de estabilidad implica que el denominador en la ecuación (17) es positivo, por lo cual el signo de esta expresión depende del numerador. Por lo tanto:
Si γh < βu, es decir, si en la función de inversión (11a) el impacto de la demanda, reflejado por el término βu, pesa más que el impacto de los factores de oferta, reflejados por el término γh, entonces una disminución en h o un aumento en la participación de los salarios sobre el producto (1−h), se traduce en una mayor tasa de crecimiento.
Así, se tienen tres situaciones: primero, una en la cual, tanto la tasa de crecimiento g como el nivel de utilización u dependen negativamente de la proporción de los beneficios sobre el producto h. Segundo, una situación en la cual g y u dependen positivamente de h. Finalmente, puede ocurrir que g esté relacionada positivamente con h pero u lo esté negativamente4. A continuación se estudian estos tres casos por medio de un análisis de estática comparativa.
Estática comparativa
Crecimiento guiado por los salarios
Si la inversión es menos sensible que el ahorro a variaciones en h y, asimismo, es relativamente más sensible a cambios en la demanda, entonces:
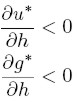 | [18] |
De acuerdo a ( 16) y ( 17), esto implica que:
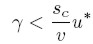 | [18a] |
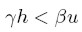 | [18b] |
En la Gráfica 2, consideremos una economía que se encuentra en el punto de equilibrio E1. Si ocurre un incremento salarial -o equivalentemente una disminución en h-, de acuerdo a la condición (18a) el ahorro disminuye en una proporción mayor que la inversión, lo que genera un exceso de demanda. En otras palabras, el incremento salarial causa un aumento en el gasto de consumo, que es mayor que la disminución en la inversión causada por la reducción de h, debido a la mayor propensión marginal a consumir de los trabajadores. Como resultado, la demanda agregada (C + I) aumenta, acrecentando el volumen de las ventas, lo que obliga a las empresas a elevar el nivel de utilización de la capacidad instalada u.

En consecuencia, las empresas se ven incentivadas a comprometerse en nuevos proyectos de inversión como respuesta al comportamiento favorable de la demanda -dado que por (18b) la inversión es relativamente poco sensible a cambios en las condiciones de oferta. De este modo, la economía alcanza el punto de equilibrio E2, en el cual, tanto el grado de utilización u*2 como la tasa de crecimiento g*2son más elevados que en E1. Asimismo, en el equilibrio E2, la ecuación (5) muestra que la tasa de beneficio aumenta como resultado de la mayor tasa de crecimiento.
Por tanto, el incremento inicial en los salarios reales tiene un efecto positivo para el conjunto de la economía, en términos del nivel de producto y de la tasa de crecimiento. De la misma forma, beneficia a todas las clases sociales, aunque la participación de los beneficios sobre el producto disminuya. Esta es la paradoja kaleckiana de los costos. Además, la paradoja del ahorro sigue siendo válida bajo estas condiciones, pues una reducción en la propensión marginal a ahorrar de los capitalistas reduce la pendiente de la curva de ahorro, aunque sin afectar la curva de inversión, de manera que la economía obtiene un equilibrio superior, similar al punto E2 que se muestra en la Gráfica 1. De esta manera, es evidente que si se verifica la condición (18), el presente modelo emula el modelo de crecimiento kaleckiano presentado, así como todos sus resultados básicos.
Crecimiento guiado por los beneficios
Si la inversión es más sensible que el ahorro ante variaciones en h y responde con más fuerza a variaciones en las condiciones de oferta que a las variaciones de la demanda, entonces:
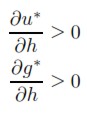 | [19] |
De donde se colige, de acuerdo a (16) y (17), que:
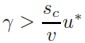 | [19a] |
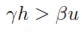 | [19b] |
En este caso, partiendo del punto de equilibrio E1 de la Gráfica 3, si hay una disminución en h como consecuencia, por ejemplo, de un incremento en los salarios reales, de acuerdo a la condición ( 19a) la inversión disminuiría en una magnitud mayor que el ahorro, lo que provoca un exceso de oferta. Además, según la condición ( 19b), la inversión es poco sensible a los cambios en la demanda en relación con los cambios en las condiciones de oferta -los costos-. En consecuencia, la caída en la inversión como resultado de la diminución en h es más grande que el aumento en el consumo debido al incremento en los salarios, por lo que la demanda agregada (C + I) se contrae. Por tanto, las firmas recortan la producción con el fin de eliminar el exceso de oferta, de modo que el nivel de utilización u disminuye. Esta situación conduce a la economía al equilibrio E2, en el cual la tasa de crecimiento g*2 y el nivel de utilización u*2 son menores que en el punto E1, lo cual implica que el incremento inicial en los salarios reales es costoso para la economía en su conjunto, pues debilita la demanda agregada y reduce la tasa de crecimiento. Al igual, dicho cambio afecta negativamente a los capitalistas, quienes ven mermada la tasa de beneficio.
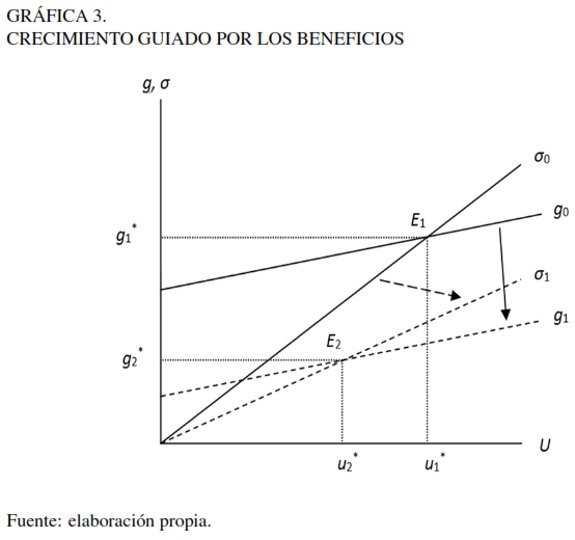
Por tanto, contrariamente a lo que se obtuvo en el primer caso, aquí se obtiene una relación inversa entre el salario real y la tasa de crecimiento, así como respecto a la tasa de beneficio. Esta es la posición defendida por la teoría neoclásica, para la cual un incremento en los salarios reales afecta negativamente la trayectoria de crecimiento, lo cual tiene como consecuencia un menor producto per-cápita en el largo plazo.
Crisis de subacumulación y sobreacumulación
Si la inversión es menos sensible que el ahorro ante variaciones en la proporción de los beneficios h, pero responde con más fuerza ante cambios en las condiciones de oferta que a las variaciones de la demanda, se tiene que:
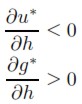 | [20] |
Que, según (16) y (17), implica:
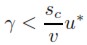 | [20a] |
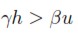 | [20b] |
Remitiéndonos ahora a la Gráfica 1, si en una economía que se encuentra en el punto de equilibrio E1 ocurre una disminución en h o, equivalentemente, un aumentoen los salarios reales, el primer efecto, de acuerdo a la condición (20a), es una caída en la inversión, pero en una cuantía menor que el ahorro. Por tanto, se genera un exceso de demanda que incentiva a las empresas a elevar sus niveles de utilización de la capacidad instalada.
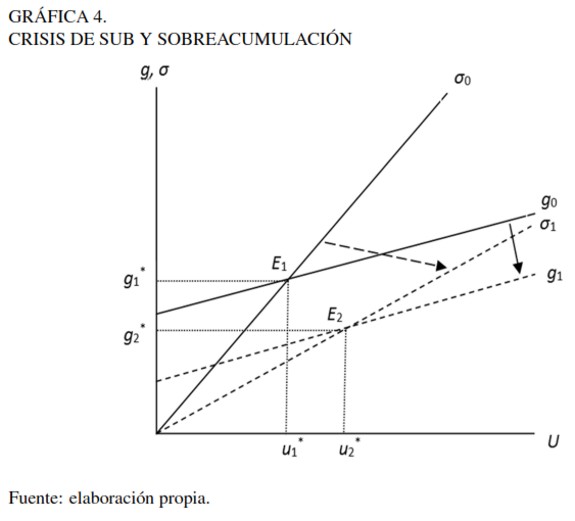
Sin embargo, según la condición (20b), la inversión es más sensible a los cambios en las condiciones de oferta que a los cambios en la demanda; por lo tanto, la inversión no aumenta y no se repone de su caída inicial. Como resultado, se termina en una situación en la que la demanda agregada es más alta, como consecuencia del mayor gasto de consumo por parte de los trabajadores, lo que se refleja en un grado de utilización más elevado (u*2 > u*1), pero en la cual la tasa de crecimiento es más baja (g*2 < g*1) debido a la menor sensibilidad de la inversión a los cambios en la demanda, pues pesa más el efecto negativo de la disminución en el margen de beneficios h. Esta situación está representada por el equilibrio E2.
Aunque el punto E2 es un equilibrio, representa lo que se podría llamar una crisis de subacumulación, pues muestra que, a pesar de la posibilidad de poder estimular la actividad económica en el corto plazo a través del gasto de consumo y altos salarios, el bajo margen de beneficio que acarrearía esta situación conduciría a bajos niveles de inversión y, por tanto, a una menor tasa de crecimiento. Por el contrario, el equilibrio E1 representa lo que se podría denominar una crisis de sobreacumulación, en la cual el alto margen de beneficios y la alta participación delos beneficios sobre el producto nacional permiten elevados niveles de inversión y, por tanto, altas tasas de crecimiento, pero con el problema de que esos elevados niveles de inversión pueden conducir a una situación en la que la capacidad productiva de la economía pueda crecer esproporcionadamente, llevando a que se presenten altos niveles de capacidad instalada excedentaria.
CONCLUSIONES
En los dos modelos de crecimiento kaleckiano presentados, la demanda tiene un rol en la determinación de la tasa de crecimiento de equilibrio. Esto contrasta con los modelos neoclásicos, en los cuales la demanda no juega ningún papel, pues las variables relevantes son determinadas por la oferta. Como se explicó, la diferencia esencial de los modelos de crecimiento kaleckianos respecto de los neoclásicos reside en el rechazo de la hipótesis de la ley de Say. Abandonar esta hipótesis permitereintroducir la demanda y obtener otros resultados interesantes. Uno de ellosatañe a la relación entre el ahorro y la inversión. Como ya se había señalado, la ley de Say implica que el ahorro genera la inversión, por lo cual la inversión no puede ser tratada como una variable independiente del ahorro. Por tanto, para la teoría neoclásica una teoría de la inversión es equivalente a una teoría del ahorro. Sin embargo, abandonar la hipótesis de la ley de Say significa abandonar el supuesto de que la oferta crea la demanda y, por consiguiente, de que el ahorro crea la inversión, de manera que estas pueden ser tratadas como dos variables separadas. Así, una teoría de la inversión ya no es equivalente a una teoría del ahorro, pues al no haber garantía de que ambas variables sean iguales, esto implica que ambas deben responder a determinantes diferentes.
En lo que atañe a la distribución del ingreso, en tanto los trabajadores y los capitalistas se diferencian por su relación respecto del capital, es de esperar que ambos grupos tengan también comportamientos diferentes. Los capitalistas, al poseer el capital y ser, por tanto, propietarios de las firmas, están forzados a ahorrar una parte de su ingreso para satisfacer las necesidades de acumulación de sus negocios. En consecuencia, una redistribución del ingreso puede tener importantes consecuencias sobre el desempeño económico y, en particular, sobre la tasa de crecimiento, dependiendo de la sensibilidad de las decisiones de los trabajadores y los capitalistas ante modificaciones en su nivel de ingreso. Aunque en el modelo kaleckiano es posible determinar los efectos de la distribución de una manera indirecta, se ignora la sensibilidad de las decisiones de los capitalistas con relación a la sensibilidad de las decisiones de los trabajadores, pues la función de inversión es afectada solamente por el comportamiento de la demanda, que es reflejada por el coeficiente de utilización u. Por tanto, implícitamente asume que en cualquier circunstancia los capitalistas prestan más atención al comportamiento de la demanda que al de sus propios beneficios.
La extensión del modelo kaleckiano hace frente a esta omisión introduciendo como un argumento adicional en la función de inversión la variable h, la cual refleja las condiciones de oferta y permite considerar de manera directa el impacto de la distribución del ingreso sobre la inversión y la tasa de crecimiento. Así, de acuerdo a este modelo aumentar la participación de los salarios sobre el producto (1 − h) puede tener un efecto positivo si los capitalistas prestan más atención al comportamiento de la demanda que al comportamiento de sus beneficios. En tales circunstancias se obtiene la paradoja kaleckiana de los costos, según la cual un incremento salarial, contrario a lo esperado por la teoría neoclásica, tiene efectos positivos en términos de la tasa de crecimiento y el empleo5. Por el contrario, si los capitalistas son muy sensibles a variaciones en los beneficios y en los costos de producción, un incremento salarial tiene un efecto negativo sobre la tasa de crecimiento y el empleo, precisamente lo esperado por la teoría neoclásica.
No hay que ignorar que en el marco de la teoría neoclásica, cuando la productividad del trabajo aumenta, un incremento salarial no tiene necesariamente los efectos negativos que predice sobre el empleo y la tasa de crecimiento, siempre que ese incremento sea inferior o igual al incremento en la productividad. Sin embargo, de acuerdo a lo expuesto en la primera sección los modelos de crecimiento kaleckiano suponen que la productividad del trabajo es constante, al menos mientras u < 1. Por tanto, en el marco de los dos modelos kaleckianos considerados, un incremento salarial puede tener un efecto positivo sobre la tasa de crecimiento y el empleo aun si la productividad del trabajo es constante.
Finalmente, aunque la teoría neoclásica aparentemente ignora el problema de la distribución del ingreso en el ámbito de la economía positiva, no logra su cometido. Al afirmar que los salarios tienen una relación negativa con el nivel de empleo y la tasa de crecimiento, implica implícitamente que una redistribución del ingreso desde los salarios hacia los beneficios (es decir, favorable a los capitalistas) es la estrategia a seguir para impulsar la contratación del trabajo, incentivar la producción y elevar la tasa de crecimiento.
NOTAS AL PIE
2 Este modelo sintetiza las contribuciones de Ramsey (1928), Cass (1965) y Koopmans (1965).
3 Esta hipótesis no afecta los resultados del modelo, puesto que, Pasinetti (1962) ha demostrado que si los trabajadores ahorran, esta decisión no afecta la condición de crecimiento de estado estable.
4 Hay un caso adicional, en el cual la tasa de crecimiento g está relacionada negativamente con h, pero el nivel de utilización u lo está positivamente. Su análisis se descarta, pues implica que los capitalistas desahorran, es decir, que tienen un propensión marginal a consumir más alta que los trabajadores y mayor a la unidad.
5 Este resultado es compatible con la llamada curva de salarios, una relación empírica según la cual ha de esperarse una relación negativa entre el nivel de los salarios y el desempleo, y que ha sido problemática para la teoría neoclásica, ya que ha tenido dificultades para explicarla. Esta relación inversa también es ilustrada por la curva de Phillips, según la cual incrementos en el salario real permiten disminuciones en la tasa de desempleo.
REFERENCIAS BIBLIOGRÁFICAS
[1] Amadeo, E. (1986). The role of Capacity Utilization in Long-period Analysis. Political Economy, 2(2), 147-185.
[2] Arestis, P. (1992). The Post-Keynesian Approach to Economics. Vermont: Edward Elgar Publishing Company.
[3] Atesoglu, H.y Smithin, J. (2006). Real wages, productivity and economic growth in the G7, 1960-2002. Review of Political Economy, 18(2), 223-233.
[4] Bhaduri, A. yMarglin, S. (1990). Unemployment and the RealWage: The Economic Basis for Contesting Political Ideologies. Cambridge Journal of Economics, 14(4),375-93.
[5] Bosworth, B. (2006, 6 de Abril). United States Saving in a Global Context. Brookings Newsletters: Economics Studies Bulletin.
[6] Cass, D. (1965). Optimum growth in an aggregative model of capital accumulation. Review of Economic Studies, 37, 233-240.
[7] Corrigan, S. (2003, 21 de mayo). US vs. Japan: Which Economy is Stronger. Mises Daily.
[8] Del Monte, A. (1975). Grado, di monopolio e sviluppoeconomico. Rivista internazionale di scienze sociali, 83, 231-263.
[9] Dutt, A. (1990). Growth, Distribution and Uneven Development. Cambridge: Cambridge University Press.
[10] Harrod, R. (1939). An Essay in Dynamic Theory. The Economic Journal, 49(193), 14-33.
[11] Hein, E. (2007). Interest Rate, Debt, Distribution and Capital Accumulation in a Post-Kaleckian Model. Metroeconomica, 58(2), 310-339.
[12] Hein, E. y Lena, V. (2008a). Distribution and growth reconsidered: empirical results for six OECD countries. Cambridge Journal of Economics, 32(3), 479-511.
[13] Hein, E. y Tarassow, A. (2008b). Distribution, aggregate demand and productivity growth: theory and empirical results for six OECD countries based on a Postkaleckia model (Working Paper 18). Germany: Macroeconomic Policy Institute, Hans Boeckler Foundation.
[14] Hein, E. y Van Treeck, T. (2007). ‘Financialisation’ in Kaleckian/Post-Kaleckian models of distribution and growth (Working Paper 7). Macroeconomic Policy Institute, Hans Boeckler Foundation.
[15] Johnson, P. (2005). Growth Theory. A Glossary of Political Economy Terms. Auburn: Auburn University.
[16] Kaldor, N. (1956). Alternative Theories of Distribution. Review of Economic Studies, 23(2), 83-100.
[17] Kalecki, M. (1956). Teoría de la dinámica económica: ensayo sobre los movimientos cíclicos y a largo plazo de la economía capitalista. México: Fondo de Cultura Económica.
[18] Kalecki, M. (1982). Ensayos escogidos sobre dinámica de la economía capitalista. México: Fondo de Cultura Económica.
[19] Kalecki, M. (1995). Teoría de la dinámica económica. México: Fondo de Cultura Económica.
[20] Keynes, J. M. (1954). The General Theory of Employment, Interest and Money.Londres: MacMillian.
[21] Koopmans, T. (1965). On the Concept of Optimal Economic Growth. New Haven: Yale University: Cowles Foundation for Research in Economics.
[22] Lavoie, M. (2003). Kaleckian Effective Demand and Sraffian Normal Prices: towards a reconciliation. Review of Political Economy, 15(1), 53-74.
[23] Lavoie, M. (2005). La economía postkeynesiana. Barcelona: Icaria editorial.
[24] Lavoie, Mark (1995). Interest rates in post-Keynesian models of growth and distribution. Metroeconomica, 46, pp. 146-177.
[25] León-Ledesma, M. y Thirwall, T. (2002). The Endogeneity of the Natural Rate of Growth. Cambridge Journal of Economics, 26(4), 441-459.
[26] Lucas, R. (1988). On the mechanics of economic development. Journal of Monetary Economics, 22, 3-42.
[27] Pasinetti, L. (1962). Rate of Profit and Income Distribution in Relation to the Rate of Economic Growth. Review of Economic Studies, 29(4), 267-279.
[28] Ramsey, F. (1928). A mathematical theory of saving. Economic Journal, 38, 543-59.
[29] Robinson, J. (1956). The Accumulation of Capital. Londres: Macmillan.
[30] Romer, P. (1986). Increasing returns and long-run growth. Journal of Political Economy, 94, 1002-1037.
[31] Rowthorn, R. (1981). Demand, RealWages and Economic Growth. Londres: Thames Papers in Political Economy, North East London Polytechnic.
[32] Setterfield, M. (2003). Supply and Demand in the Theory of Long-run Growth: introduction to a symposium on demand-led growth. Review of Political Economy, 15(1), 23- 32.
[33] Sala I Martin, X. (1994). Apuntes de crecimiento económico. Barcelona: Antoni Bosch.
[34] Sawyer, M. (2001). Kalecki on Imperfect Competition, Inflation and Money. Cambridge Journal of Economics, 25, 245-261
[35] Solow, Robert (1956). A Contribution to the Theory of Economic Growth. The Quarterly Journal of Economics, 70(1), 65-94.
[36] Stockhammer, E. (1999). Robinsionian and Kaleckian Growth: An Update on Post-Keynesian Growth Theories (Working Paper 67). Viena: Vienna University of Economics and Business Administration.
[37] Stockhammer, E. (2004). Is There an Equilibrium Rate of Unemployment in the Long Run? Review of Political Economy, 16(1), 59-77.
[38] Stockhamer, E., Onaran, O. y Ederer, S. (2009). Functional income distribution and aggregate demand in the Euro-area. Cambridge Journal of Economics, 33(1), 139-159.
[39] Taylor, L. (1991). Income Distribution, Inflation, and Growth. Massachusetts: The MIT Press.