ESTIMACIÓN DE LA EFICIENCIA DEL SECTORMETALMECÁNICO EN COLOMBIA: ANÁLISIS DE LA FRONTERA ESTOCÁSTICA
Gerardo A. Buchelli Lozano1
Jhon Jairo Marín Restrepo2
1 Magister en Economía y docente auxiliar de la Universidad Católica de Pereira. E-mail: gerardo.buchelli@ucp.edu.co. Dirección de correspondencia: Manzana 41 Casa 39 Villa del Prado,(Pereira, Risaralda).
2 Magister en Economía y docente auxiliar de la Fundación Universitaria del Área Andina. E-mail: jjmarin@funandi.edu.co. Dirección de correspondencia: Calle 101 No. 16b12, Casa 36, Belmonte, (Pereira, Risaralda).
Este artículo fue recibido el 10 de mayo de 2010, la nueva versión el 7 de septiembre de 2011 y su publicación aprobada el 14 de octubre de 2011.
Resumen
En este documento se evalúa el desempeño del sector metalmecánico en Colombia, durante el período 1998-2007, utilizando técnicas de frontera estocástica (SFA) que, a través de la estimación de las desviaciones de una función ideal de costos, permiten medir los niveles de eficiencia económica de las diversas unidades de producción. Los resultados indican que existen diferencias significativas en el desempeño de los doce departamentos incluidos en el análisis, por lo que se sugiere que se podrían obtener importantes ganancias en términos de reducción de costos si las unidades de producción se acercaran a los niveles de operación de las más eficientes. Adicionalmente, se encuentra que, durante el periodo de análisis, se observa un cambio significativo en la eficiencia de costos del sector, lo cual se puede explicar debido al impacto de la crisis económica registrada en el país, a finales de la década de los noventa, sobre las unidades de producción del sector.
Palabras clave: fronteras estocásticas, eficiencia económica, productividad, metalmecánica.
JEL: C23, D20, D24, L64.
Abstract
This paper evaluates the performance of the metalworking sector in Colombia, between 1998 and 2007, using stochastic frontier techniques (SFA), which, through the estimation of the deviations from an ideal function of costs, measure levels economic efficiency of various production units. The results indicate significant differences in the performance of the 12 departments included in the analysis, suggesting that each could achieve significant gains in terms of cost reduction if the production units were closer to the production levels of operation of the more efficient. Additionally, we find that during the period of analysis there is a significant change in the cost efficiency of the sector. Said efficiency can be explained by the impact, the production units of the sector, and the economic crisis in the country in the late nineties.
Keywords: stochastic frontiers, economic efficiency, productivity, metalworking.
JEL: C23, D20, D24, L64.
Dans ce document on évalué le déroulement du secteurmétal-mécanique en Colombie, pendant la période 1998-2007, en utilisant des techniques de frontière stochastique (SFA), à travers de l'estimation des déviations d'une fonction idéale de coûts qui permettent de mesurer les niveaux d'efficacité économique des diverses unités de production. Les résultats indiquent qu'existent des différences significatives dans le dégagement des douze départements inclus dans l'analyse, par cela on suggère que des profits importants pourraient être obtenus dans des termes de réduction de coûts si les unités de production s'approchaient aux niveaux d'opération des plus efficientes. En outre, on trouve que pendant la période d'analyse, un changement significatif est observé par rapport à l'efficacité de coûts du secteur, ce qui peut être expliqué grâce à l'impact de la crise économique enregistrée dans le pays, à la fin de la décennie de quatre-vingt-dix, sur les unités de production du secteur.
Mots clés : frontières stochastiques, efficacité économique, productivité, métalmécanique, Colombie.
JEL: C23, D20, D24, L64.
Desde 1990 el país asume el compromiso y el desafío de insertarse en la dinámica de internacionalización. Sin embargo, solo hasta julio de 2004, con el documento del Consejo de Política Económica y Social (Conpes, 3297), el Gobierno nacional inicia la construcción de una agenda interna para la productividad y la competitividad, delegando al Departamento Nacional de Planeación (DNP) la coordinación, priorización y fomento de la productividad y competitividad del país. Específicamente, y a partir de la iniciativa de los productores de todos los eslabones de la cadena productiva en metalmecánica y siderurgia, el DNP presentó el documento sectorial sobre dicho sector industrial en el año 2007; en particular, los departamentos de Risaralda, Caldas y Atlántico se comprometen con una mayor articulación entre la producción y la comercialización del sector, mejorando para ello tanto su infraestructura vial como la producción del sector metalmecánico.
A parir de la Encuesta Anual Manufacturera (EAM) se evidencia que durante el periodo comprendido entre los años 2000 y 2007 la producción del sector metalmecánico registró un incremento de su participación sobre el sector industrial del país; su contribución en la producción industrial nacional pasó del 8,9%al 11,3%. El mayor dinamismo se observa en los departamentos de Cauca, Bolívar y Risaralda, en los que las tasas de crecimiento promedio alcanzaron 63,7%, 20,9% y 20,5%, respectivamente. Adicionalmente, vale la pena señalar que los departamentos de Risaralda, Caldas y Atlántico realizaron una apuesta productiva por el sector de metalmecánica, buscando incrementar la articulación entre la producción y la comercialización. Con este fin, se ha venido adelantando un proceso de mejoramiento de la infraestructura vial y de los servicios públicos existentes, así como el aumento de la producción metalmecánica en estos departamentos (DNP, 2007).
Teniendo en cuenta la importancia de la metalmecánica en la economía nacional, es importante evaluar si esta opera en condiciones de eficiencia, dado que una mayor eficiencia permitiría alcanzar, con la misma cantidad de insumos, mayores niveles de producción o menores niveles de costos, generando ahorros en el sector. Es pertinente señalar que los desarrollos teóricos y metodológicos del concepto productividad giran en torno a dos perspectivas. Por una parte, se encuentran los análisis de la productividad total de los factores, que utilizan los planteamientos de Solow (1957), y por otra, se encuentran los análisis de eficiencia técnica, a partir del trabajo pionero de Farrell (1957). Específicamente, desde la última perspectiva se desprenden los análisis de eficiencia que utilizan la metodología de frontera estocástica, empleada en el presente documento.
En cuanto al análisis empírico, el trabajo propuesto por Farrell (1957) se apoya en técnicas de frontera estocástica que, a través de la estimación de las desviaciones de una función ideal de producción o de costos, se utilizan para medir los niveles de eficiencia en diferentes unidades productivas. Como se plantea en Melo y Espinosa (2005), una de las ventajas de aplicar análisis de frontera con respecto a las técnicas econométricas tradicionales es que provee medidas específicas de ineficiencia, que no siempre son el resultado del comportamiento directo de la unidad de producción. Así, las desviaciones pueden estar originadas en eventos que se encuentran bajo o fuera del control de dichas unidades de producción.
En el presente documento las técnicas de frontera estocástica se utilizan para estimar los niveles de eficiencia económica del sector metalmecánico, empleando como unidad de producción los 12 departamentos de Colombia que reportan información de dicho sector: Antioquia, Atlántico, Santafé de Bogotá, Bolívar, Caldas, Cauca, Cundinamarca, Norte de Santander, Quindío, Risaralda, Santander y Valle del Cauca, durante el periodo 1998-2007. Los datos utilizados para realizar el análisis empírico provienen de la Encuesta Anual Manufacturera (EAM), según clasificación CIIU (revisión 2, de tres dígitos).
Las técnicas de frontera estocástica han sido ampliamente empleadas para medir los niveles de eficiencia a través de diferentes unidades de producción y en distintos sectores económicos, incluyendo el sector público y el privado. Con relación al sector metalmecánico, la técnica no se ha utilizado directamente; sin embargo, varios estudios han estimado la eficiencia utilizando el análisis de frontera estocástica para diferentes industrias del sector manufacturero, incluyendo la metalmecánica. Para el caso colombiano, por ejemplo, Tyler y Feil (1979) estiman la ineficiencia de pequeñas y medianas empresas de varias industrias colombianas, incluyendo las metalmecánicas. Estos autores, manejando una función Cobb-Douglas, encuentran que varias empresas podrían obtener ganancias en términos de eficiencia técnica. De igual forma, a nivel internacional se encuentran trabajos que hacen uso de las técnicas de frontera estocástica para estimar la eficiencia de empresas manufactureras,incluyendo las metalmecánicas (véase por ejemplo Díaz y Sánchez, 2008; Managi, Opaluch y Grigalunas, 2006).
Teniendo en cuenta que las unidades de producción utilizadas en el análisis empírico son los departamentos, se destaca que las técnicas de frontera estocástica se han empleado ampliamente en análisis de tipo regional. Por ejemplo, Acevedo y Ramírez (2005) realizan un estudio para identificar las disparidades regionales en la eficiencia técnica del sector de confecciones en Colombia, aplicando el método de análisis de fronteras estocásticas con datos de panel durante el período 1992- 2001. Los autores estiman una función de producción de frontera estocástica para once departamentos, y concluyen que la evolución de la eficiencia técnica promedio para el sector de confecciones muestra una leve tendencia ascendente durante el periodo analizado.
Otro trabajo que recurre a la técnica de frontera estocástica para realizar mediciones de eficiencia a nivel regional es el de Melo (2005), quien analiza el impacto de la descentralización fiscal en la provisión de la educación pública en Colombia. Los resultados muestran la presencia de altos niveles de ineficiencia en costos y producción en los diferentes departamentos del país. Recientemente, Barrientos, Tobón y Gutiérrez (2009) establecen los principales determinantes de la eficiencia del sector del calzado y marroquinería de cuero, a partir de ciertos factores, prácticas empresariales y ambientes específicos; ellos utilizan la técnica de frontera estocástica con una función de producción Cobb-Douglas, señalando que, si bien con las nuevas maquinarias podrían incrementar las ventas, en la práctica, las tecnologías son convencionales y tienen rezagos en temas de innovación, investigación y desarrollo, lo que explica el hecho de que las empresas se alejen, en promedio, en un 33% de sus posibilidades de producción.
Para el caso colombiano, no obstante, no se han adelantado estudios sobre la eficiencia del sector metalmecánico utilizando técnicas de frontera estocástica, lo cual es el principal objetivo del presente trabajo de investigación.
El documento está estructurado en seis secciones: la primera corresponde a la presente introducción; en la segunda, se aborda la contextualización del sector metalmecánico; en la tercera, se presenta el modelo teórico y la metodología a partir de una revisión teórica y de los antecedentes de la investigación, se aborda el concepto de eficiencia productiva y se complementa luego con la perspectiva de eficiencia en costos; en la cuarta sección se realiza la especificación del modelo Data Panel y se presenta una descripción de las variables; en la quinta sección se encuentran los resultados del ejercicio empírico y el análisis de la eficiencia en costos, bajo la técnica de frontera estocástica; finalmente, en la sexta sección se presentan las conclusiones del trabajo.
CONTEXTUALIZACIÓN DEL SECTOR METALMECÁNICO
Teniendo en cuenta la heterogeneidad del aparato productivo colombiano, se implementan estrategias de desarrollo económico diferenciadas con el ánimo de potencializar sectores específicos de la economía. En particular, de acuerdo a los intereses y las preocupaciones de los productores de todos los eslabones de la cadena productiva del sector de la metalmecánica y la siderurgia, el DNP le da prioridad a este y publica el Documento sectorial metalmecánica y siderurgia, en el año 2007.
En dicho documento sectorial, en Risaralda se comprometen a incrementar el valor de la producción metalmecánica en un 100% para el año 2017, con el fin de suplir el mercado nacional e internacional; Caldas asume el compromiso de impulsar el sector de la metalmecánica, haciendo énfasis en las herramientas, la maquinaria y los equipos, y Atlántico, por su parte, plantea impulsar la producción metalmecánica. En cada uno de los anteriores departamentos se busca estimular la gestión y generación de nodos de producción metalmecánica regional, propiciando la concentración de empresas en cadenas productivas, es decir, clúster metalmecánicos a partir de los cuales se incremente la productividad y competitividad, de acuerdo con una plataforma que sustente el crecimiento de una dinámica exportadora y la generación de empleos productivos.
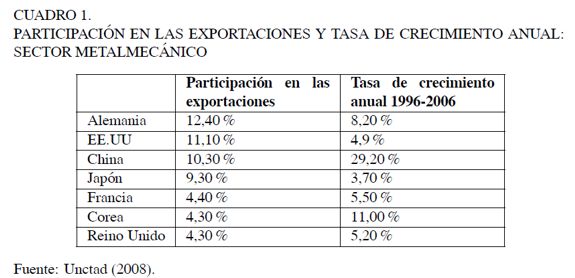
En tal sentido, Cavallé (1975) propone que los países industrializados se caracterizan porque sus industrias básicas están relacionadas con las de metal y resalta el encadenamiento con otras industrias como maquinaria, electrodomésticos, automotores, construcción y una serie de procesos industriales que proveen bienes y servicios en la economía. En efecto, a nivel internacional la metalmecánica es una industria dinámica, dadas sus constantes innovaciones en procesos y componentes. En particular, mientras los productos del sector aportaban el 18% del intercambio mundial en 1972, este porcentaje ascendió a 37% en el año 2006. Como se observa en el Cuadro 1, Alemania se constituye en el principal exportador mundial con el 12,4% del total, seguido por Estados Unidos, China, Japón, Francia, Corea y Reino Unido, que en conjunto participan con el 60% de las exportaciones totales de productos metalmecánicos en el 2006.
La industria metalmecánica elabora artículos metálicos a partir, tanto de la manipulación mecánica de los metales como del ensamble de piezas metálicas previamente elaboradas, ambos procesos realizados con técnicas de modelados en frío y transformaciones o modificaciones en el volumen del material; además, presenta esquemas de subcontratación en el proceso productivo e incorporaciones recientes de tecnología, a través de equipos de producción modernos que buscan mejorar los niveles de calidad, una reducción en los tiempos de entrega y la capacidad para producir lotes pequeños.

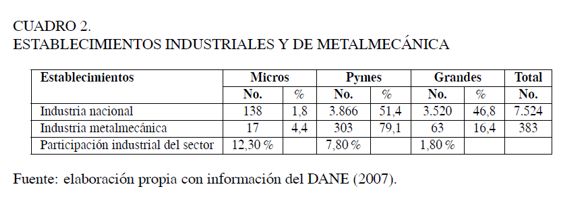
Es importante señalar que las empresas colombianas del sector metalmecánico ofrecen menores tiempos de entrega, además de la posibilidad de producir lotes pequeños y hacer entregas de menor valor que las de los competidores internacionales. Sin embargo, a pesar de que la mayoría de las empresas de la cadena son pequeñas y medianas, la producción nacional se concentra en empresas grandes. En el Cuadro 2 se observa que el 79% de los establecimientos dedicados a la producción del sector metalmecánico corresponden a la pequeña y mediana industria, y el 16% se clasifica dentro de las grandes. Adicionalmente, a nivel industrial se observa que dentro de las industrias grandes del país solo el 1,8%se encuentran en el sector metalmecánico. La mayor participación se registra en el grupo clasificado como microempresas, con una participación de 12,3%.
En términos del proceso productivo, la industria metalmecánica recibe una serie de insumos que son distribuidos en laminado, reducción y fundición -según sea el requerimiento del producto final-, y clasificados en artículos metalmecánicos y maquinaria no eléctrica. El primer grupo corresponde a los bienes terminados empleados en el hogar, las oficinas y las ferreterías, en tanto que el segundo grupo de productos se constituye, generalmente, en todas aquellas maquinarias primas necesarias por otros sectores o grupos industriales.
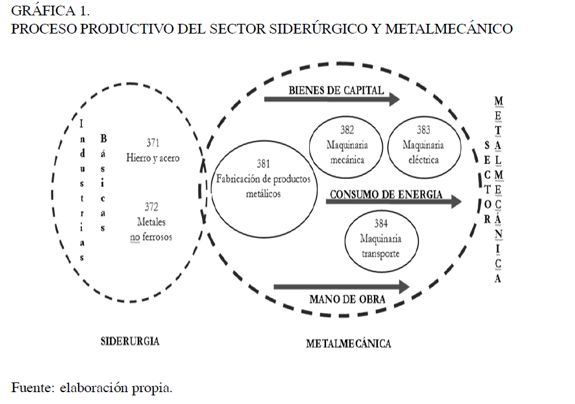
Adicionalmente, se destaca que desde la clasificación industrial CIIU (Rev. 2 de tres dígitos), se presenta un eslabonamiento en la fabricación de productos metálicos3 hacia adelante, en la medida en que aporta insumos para la obtención de las herramientas requeridas en el proceso productivo de las siguientes agrupaciones, así como en la elaboración de partes y piezas indispensables para su fabricación. El proceso del sector siderúrgico y metalmecánico se puede observar en forma esquemática en la Gráfica 1.
El proceso completo considera tanto a las industrias básicas o siderúrgicas como a las industrias metalúrgicas de transformación o metalmecánica. Sin embargo, como las dos industrias se diferencian de forma significativa en el proceso y la estructura de producción, es importante precisar que en el presente trabajo se aborda el análisis de eficiencia del sector metalmecánico. En términos de la información agregada del sector, se parte de la fabricación de productos metálicos (CIIU 381), que eslabona hacia adelante con las demás agrupaciones del sector y obtiene las herramientas requeridas tanto en la construcción de maquinariamecánica (CIIU 382) como en la fabricación de maquinaria, aparatos, accesorios y suministros eléctricos (CIIU 383), generando así insumos y piezas importantes para la construcción de equipo y material de transporte (CIIU 384). Una vez agrupada la información de los cuatro subsectores, se consolida el sector metalmecánico.
Es importante resaltar que, durante los últimos años, la estructura de costos del proceso productivo del sector metalmecánico ha evidenciado una significativa transformación debido a la incorporación de nueva tecnología, lo que ha contribuido al mejoramiento de la obtención de materias primas y al incremento del consumo de energía eléctrica. A partir de ello, se plantea que los factores productivosmás relevantes en la producción metalmecánica son la mano de obra, los bienes de capital y el consumo de energía eléctrica; por tanto, en la estructura de costos se deben considerar los costos por salarios, la tasa de interés asociado al costo de capital y el precio del k-watio de energía.
MODELO TEÓRICO Y METODOLOGÍA
Medidas de eficiencia
Inicialmente se debe reconocer que la eficiencia es un concepto relativo y que su determinación se realiza a partir de la comparación entre diferentes alternativas disponibles, obtenidas con el uso de combinaciones diversas de recursos productivos. Los niveles de producción deben considerar el costo de transformación, el cual se compara con el objetivo de identificar el mejor uso de los factores productivos, determinando la opción más eficiente desde la perspectiva productiva, en condiciones de escasez y usos alternativos. Bajo esta perspectiva, no existe un único punto de referencia en el que las firmas sean eficientes.
En cuanto al concepto de eficiencia técnica, se debe entender como aquella situación en la que una unidad de producto seleccionado corresponde al máximo nivel de producción posible con una combinación de insumos. Según Koopmans (1951), una combinación factible de insumos y productos es técnicamente eficiente si no es técnicamente posible aumentar algún producto y/o reducir algún insumo sin reducir simultáneamente al menos otro producto y/o aumentar al menos otro insumo.
Koopmans (1951), Debreu (1951) y Farrell (1957), además del concepto de eficiencia técnica, incorporan el de eficiencia asignativa, asociado a la eficiencia en precios. Desde la teoría microeconómica, si la firma busca la minimización de costos, en términos de Farrell (1957), deberá seleccionar aquella combinación de insumos y productos técnicamente eficientes y, dados los precios de mercado de los factores productivos, con el costo más bajo posible. El aporte de Farrell (1957) es un punto de referencia clave para cualquier estudio propuesto sobre la eficiencia productiva. De hecho, Farrell es el primero en proponer empíricamente la medición de la eficiencia a través del cálculo de índices de eficiencia con las combinaciones de insumos que se comportan de manera óptima en la minimización de costos, para obtener de esta forma la frontera eficiente de producción.
Eficiencia en costos
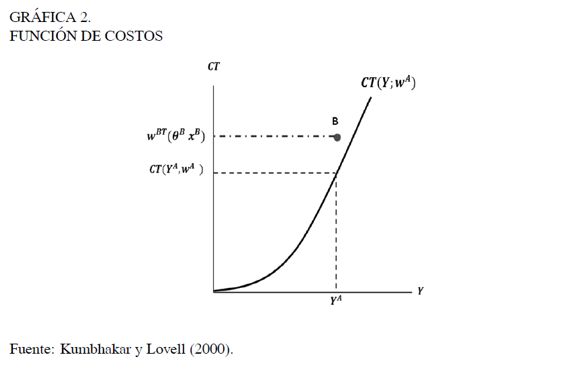
La función de costos CT(Y,w), en la cual se centra el análisis empírico del documento, indica el costo mínimo en que incurre una firma o unidad de producción, en cada nivel de producción Y, dada una tecnología y la remuneración de los diferentes factores productivos x = (x1, x2, . . . , xn), a los precios de mercado dados w = (w1, w2, . . . , wn).
En la Gráfica 2 se observa el comportamiento de una función de costos acorde con el proceso de optimización; cualquier nivel de producción cuyo costo total se sitúe por encima de esta función se considerará ineficiente. Por ejemplo, el punto B, que se encuentra por fuera de la función de costos, indica que las cantidades Y A se producen a un costo mayor -CTB = wxB- al que sería óptimo. De esta forma, se podría determinar el grado de eficiencia del costo (EC) de la observación B, con un índice a partir del cociente entre el costo óptimo y el costo incurrido en la producción por fuera de la función, es decir:
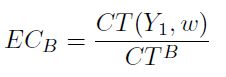 | [1] |
Este índice presenta las siguientes características: (i) es una fracción comprendida entre 0 y 1; (ii) es homogéneo de grado −1 en los factores productivos; (iii) es homogénea de grado cero en los precios de los factores y, (iv) no es decreciente en la producción.
Como lo sugiere Lovell (1993), las medidas de eficiencia económica requieren de la especificación de un objetivo económico y de la información de los precios de mercado. En particular, si el objetivo de una unidad de producción es la minimización de los costos, una medida de eficiencia de costos corresponderá a la relación entre el costo mínimo y el costo observado. La firma presentará costos superiores al nivel que define la frontera en caso de que los factores de producción no se estén utilizando completamente, es decir, que su uso sea mayor al requerido en el proceso productivo o que no se estén combinando adecuadamente, lo queimplicaría que el costo está por encima del óptimo. La primera causa se relaciona con problemas de eficiencia técnica, mientras que la segunda se relaciona con eficiencia de asignación; precisamente, la eficiencia en costos es la que recoge estos dos problemas.
En tal sentido, Greene (1993) sugiere la posibilidad de que un productor que resulta ser eficiente a partir de una función de producción, sea ineficiente al utilizarse una frontera de costos; esto sucede porque las medidas de eficiencia obtenidas con la frontera de costos contienen tanto la eficiencia técnica como la de asignación, mientras que las calculadas a partir de la frontera de producción contienen solo la primera.
Metodología
Desde mediados del siglo pasado se advierte una preocupación de los economistas por desarrollar teórica y metodológicamente el concepto de eficiencia. La formalización de su medición se ha realizado desde dos perspectivas. La primera utiliza el concepto de productividad total de los factores (PTF) y su principal autor es Solow (1957); la segunda se inicia con el trabajo pionero de Farrell (1957), según el cual las medidas de eficiencia surgen de modelos de frontera como la distancia entre una observación y el valor que predice el modelo teórico. Los modelos de frontera más utilizados para estimar medidas de eficiencia son las fronteras de producción y de costos.
Las medidas de eficiencia técnica a partir de las fronteras de producción y de costos han convertido a Farrell (1957) en el autor más influyente con relación al estudio de la eficiencia productiva; su principal contribución fue, precisamente, proponer una manera de medir empíricamente la eficiencia a partir de la cual se presentan alternativas diversas y se mejora su formulación. Por ejemplo, Aigner y Chu (1968) emplean una función de producción tipo Cobb-Douglas y, con una técnica de programaciónlineal a través de la minimización de los residuales, logran determinar la eficiencia técnica de la industria.
Sin embargo, al proponer la función paramétrica de los factores productivos con una ineficiencia técnica aditiva a la distribución de la perturbación, se logra atribuir dicha ineficiencia a todo el error estocástico. Con el fin de solucionar este inconveniente, Aigner, Lovell y Schmidt (1977) plantean un modelo de error compuesto con frontera estocástica, apoyados en una función de costos con la que se pretende determinar un costo mínimo, con la perturbación aleatoria integrada por un término simétrico positivo para incorporar la aleatoriedad del proceso productivo y otro negativo para capturar la ineficiencia en los costos de la empresa.
Desde el componente metodológico existen dos aproximaciones posibles para la construcción de fronteras, con las cuales se pueden determinar las medidas de eficiencia: la aproximación de programación matemática y la aproximación econométrica. La primera es una técnica no paramétrica conocida como análisis envolvente de datos (DEA, por sus siglas en inglés), que utiliza programaciónmatemática para determinar el conjunto de observaciones que generan la frontera -que no requiere necesariamente de una forma funcional previa-. La segunda, a través de técnicas de estimación econométrica conocidas como técnicas de frontera estocástica, supone una forma funcional para la frontera de producción, costos o beneficios, según sea el caso, y la estimación de los parámetros de la función.
La principal diferencia entre las dos es que la aproximación econométrica es estocástica y, por lo tanto, distingue los efectos del ruido aleatorio de la ineficiencia, mientras que la aproximación de programación es no estocástica y no diferencia entre estos dos conceptos (Lovell, 1993); precisamente, a pesar de que la técnica no paramétrica es más flexible, se utiliza la frontera estocástica para determinar específicamente el componente de error atribuible a la ineficiencia y para reconocer que los resultados entre las dos no son comparables.
En el presente trabajo se realiza un análisis de eficiencia económica, empleando para ello una función de costos translogarítmica, en la cual el costo total es una función de los precios de los insumos y del nivel de producción, como se observa en la ecuación (2).
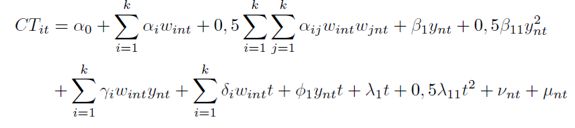 | [2] |
Donde CTit corresponde al logaritmo del costo total; ynt al logaritmo del producto; wint al logaritmo del precio del i − ésimo insumo; t es una tendencia temporal que se incluye como proxy del cambio tecnológico; ν hace referencia al error estocástico (ruido), y μ es el término que captura la ineficiencia de los costos. Las demás letras griegas corresponden a los diferentes parámetros a ser estimados, teniendo en cuenta que los subíndices n y t se refieren a las unidades de producción (departamentos) y al periodo de tiempo, respectivamente. Como se mencionó, la ineficiencia en costos posee la ventaja de recoger el efecto combinado, tanto de la ineficiencia técnica como de la ineficiencia asignativa.
Siguiendo el planteamiento teórico sobre las funciones de costos, se imponen restricciones de homogeneidad sobre la función de costos, es decir, se debe cumplir que la función sea homogénea de grado 1 en los precios de los insumos, así:
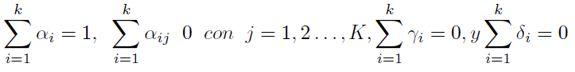 | [3] |
ESPECIFICACIÓN DEL MODELO, DATOS DE PANEL Y DESCRIPCIÓN DE LAS VARIABLES
En cuanto al análisis econométrico, inicialmente Farrell (1957) propone la estimación de los valores medios de la función de producción. Más adelante, Aigner y Chu (1968) realizan una minimización de los residuales incorporados en una función de producción Cobb-Douglas, con el fin de calcular la eficiencia técnica de la industria. Posteriormente, Aigner, Lovell y Schmidt (1977) atribuyen la ineficiencia al error estocástico y proponen una solución, basados en el modelo de error compuesto con frontera estocástica.
Finalmente, Meeusen y Van Den Broeck (1977) desarrollan la conceptualización de la frontera estocástica, a partir de la cual se consolida la referenciametodológica de esta línea de estudio sobre la eficiencia, en la que se parte de una función de comportamiento eficiente, sea de producción, de costos o de beneficios, según el caso a investigar. Así, las técnicas de frontera estocástica son extensiones del modelo de regresión que tienen su base en la premisa microeconómica de que las funciones de producción y de costos representan el máximo producto o el mínimo costo. La principal diferencia con las regresiones tradicionales es que el término de error tiene dos componentes: un ruido aleatorio y un componente no negativo conocido como ineficiencia. Así, la estructura básica de un modelo de frontera es:
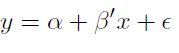 | [4] |
Donde se asume que el termino de error tiene dos componentes 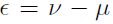 para las funciones de producción
para las funciones de producción 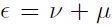 para las funciones de costos; ν es una variable aleatoria con media cero que captura el ruido, bajo la idea de que las desviaciones de la frontera no están completamente bajo el control del productor, y μ es el componente que recoge la ineficiencia. Si una unidad de producción es completamente eficiente, μ = 0 y las desviaciones de la frontera son completamente aleatorias. En la función de costos, el costo mínimo se calcula como una perturbación aleatoria compuesta por un término simétrico positivo, de tal forma que se incorpora la aleatoriedad del proceso productivo, y otro negativo con el fin de separar la ineficiencia en los costos de la firma.
para las funciones de costos; ν es una variable aleatoria con media cero que captura el ruido, bajo la idea de que las desviaciones de la frontera no están completamente bajo el control del productor, y μ es el componente que recoge la ineficiencia. Si una unidad de producción es completamente eficiente, μ = 0 y las desviaciones de la frontera son completamente aleatorias. En la función de costos, el costo mínimo se calcula como una perturbación aleatoria compuesta por un término simétrico positivo, de tal forma que se incorpora la aleatoriedad del proceso productivo, y otro negativo con el fin de separar la ineficiencia en los costos de la firma.
Bajo este método se estiman los parámetros de la frontera y se asigna una distribución estadística a cada perturbación por máxima verosimilitud, calculando con este procedimiento la eficiencia de cada firma o unidad de producción a partir del valor estimado para la perturbación. Al proponer una forma funcional, especificando un posible comportamiento eficiente de las firmas, se presenta la ventaja de que los parámetros estimados aportan los índices de eficiencia, facilitando la comparación de las hipótesis sobre los resultados y la estimación de la frontera estocástica, y diferenciando las dos causas que generan las desviaciones con respecto a la frontera: la ineficiencia y el error aleatorio.
Es importante señalar que Farrell (1957) considera el problema dual del productor, es decir, la maximización de la producción equivalente a la minimización de los costos. Así, cuando se seleccionan las combinaciones de insumos óptimos a partir de una función de producción, se puede estudiar de manera alterna la eficiencia económica con una función de costos. En el presente trabajo esta opción se presenta como alternativa para medir la eficiencia económica, estimando así una frontera de costos translogarítmica. Si las firmas no logran minimizar los costos, se ubicarán por encima de la frontera, indicando la presencia de ineficiencia técnica o de ineficiencia asignativa.
Para estudiar el comportamiento de las firmas en un modelo de minimización de costos, se requiere de una muestra de i = 1, . . . , I productores en la que cada uno de ellos emplea un vector de insumos  , con precios
, con precios  a partir de los cuales se obtiene un producto Qi > 0. En el proceso se incluye la variable de costos como la sumatoria del producto de los insumos utilizados por su precio
a partir de los cuales se obtiene un producto Qi > 0. En el proceso se incluye la variable de costos como la sumatoria del producto de los insumos utilizados por su precio 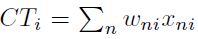 . Con el fin de estimar la eficiencia de costos se utiliza la siguiente función:
. Con el fin de estimar la eficiencia de costos se utiliza la siguiente función:
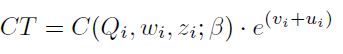 | [5] |
Donde:
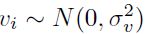 captura los efectos de la perturbación aleatoria.
captura los efectos de la perturbación aleatoria.
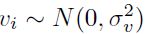 recoge el costo de ineficiencia en la asignación de insumos.
recoge el costo de ineficiencia en la asignación de insumos.
β es el vector de parámetros.
Al considerar una forma funcional translogarítmica, se tendrá:
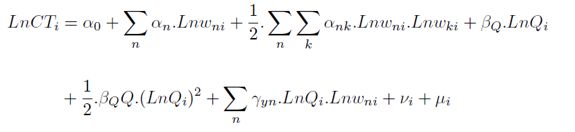 | [6] |
Considerando que:
Ln CTi es el logaritmo del costo total.
Ln Qi es el logaritmo de la producción.
Ln wni y Ln wki es el logaritmo del precio de los insumos n y k.
νi es el término de error estocástico.
μi es el término que captura la ineficiencia en costos de producción.
La anterior forma funcional considera la existencia de simetría y el supuesto de homogeneidad de grado uno en los precios de los insumos, garantizado el cumplimiento de las siguientes condiciones:
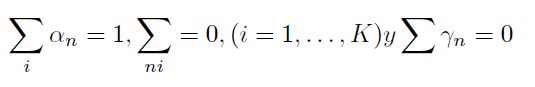 | [7] |
Las anteriores restricciones se imponen fácilmente en la estimación del modelo, en la medida que los k − 1 precios de los insumos se deflacten por el precio del insumo k−ni. En particular, como lo sugieren Coelli, Estache, Perelman y Trujillo (2003), los parámetros asociados al insumo k−simo se pueden calcular utilizando los parámetros estimados y las restricciones definidas con anterioridad.
Datos de panel en la verificación empírica
El análisis econométrico se realiza a partir de un análisis de frontera estocástica, para lo cual se estima una función de costos translogarítmica en el sector metalmecánico. El ejercicio busca explicar no solo las ineficiencias en el tiempo, sino también los errores de asignación sectoriales, utilizando información de la EAM, según clasificación CIIU (revisión 2, de tres dígitos). Teniendo en cuenta que el análisis empírico incluye información de doce departamentos, durante el periodo de tiempo comprendido entre 1998 y 2007, es necesario recurrir al análisis de frontera estocástica con datos de panel, con el fin de determinar la eficiencia económica de costos del sector metalmecánico en Colombia durante dicho periodo.
De acuerdo con Schmidt y Sickles (1984), las estimaciones mediante datos de panel evitan tres problemas, a saber: i) la eficiencia técnica se puede estimar consistentemente a medida que T →∞; ii) no se requieren supuestos de distribución para el término de ineficiencia, y iii) la estimación de los parámetros y el termino de ineficiencia se puede realizar sin asumir que la ineficiencia técnica está correlacionada con los regresores.
La utilización de datos de panel permite la estimación de los parámetros a través de efectos fijos o aleatorios. Dichos estimadores tienen diferentes criterios sobre la necesidad de utilizar supuestos de distribución en el término de eficiencia (u) y el requerimiento de asumir correlación entre u y los demás regresores. En particular, en el modelo de efectos fijos la consistencia no depende de la correlación entre u y los regresores, o del supuesto de distribución de u. Sin embargo, aunque el intercepto para cada unidad de producción puede ser estimado consistentemente, no existe una forma de separar el intercepto. Este modelo se recomienda cuando t es grande y n es pequeño.
No obstante, una de las desventajas de esta aproximación es que no permite variables invariantes en el tiempo. Por su parte, el modelo de efectos aleatorios se puede estimar utilizando mínimos cuadrados generalizados (MCG) o métodos de máxima verosimilitud. La estimación a través de MCG se recomienda cuando n es grande y t pequeña; no requiere supuestos de distribución para u y, para obtener parámetros consistentes e insesgados, u no debe estar correlacionado con los regresores.
Siguiendo a Melo y Espinosa (2005), es importante señalar que en la estimación a través de los métodos de máxima verosimilitud los componentes del término de error se asumen independientes y se requiere de un supuesto de distribución para μ. Las distribuciones más comunes son media-normal, normal truncada y exponencial (Greene, 1993; Jondrow et al., 1982; Battese y Coelli, 1988). Estas distribuciones permiten separar los dos componentes del término de error y estimar μ para cada observación. En el caso particular de la media normal, se asume que u es una variable aleatoria que se distribuye de acuerdo con valor absoluto de  variable, y la media condicional de la distribución está dada por la ecuación (8).
variable, y la media condicional de la distribución está dada por la ecuación (8).
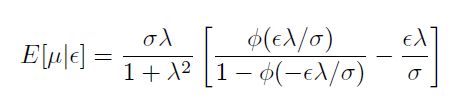 | [8] |
Donde ϕ y φ son funciones de distribución de densidad de la distribución normal estándar y 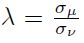 y
y 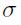 corresponde a la desviación estándar del término de error
corresponde a la desviación estándar del término de error 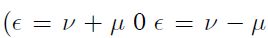 . En el modelo normal truncado μ se distribuye como el valor absoluto de una normal, pero con media diferente de cero
. En el modelo normal truncado μ se distribuye como el valor absoluto de una normal, pero con media diferente de cero 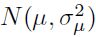 . Así, la distribución contiene un parámetro adicional μ que debe ser estimado. Para obtener la media de la distribución condicional, la expresión
. Así, la distribución contiene un parámetro adicional μ que debe ser estimado. Para obtener la media de la distribución condicional, la expresión 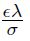 se cambia por
se cambia por 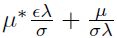 en la ecuación (8). Finalmente, en el modelo exponencial la media de distribución condicional se cambia por:
en la ecuación (8). Finalmente, en el modelo exponencial la media de distribución condicional se cambia por:
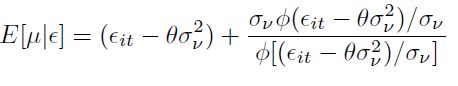 | [9] |
En tal sentido, Melo (2005) plantea que, en la literatura empírica, diferentes autores han encontrado que la ineficiencia, determinada a partir de diferentes formas de estimación y utilizando diferentes supuestos de distribución del término de ineficiencia, puede presentar algunas variaciones. Sin embargo, la clasificación de las unidades de producción que se obtienen a partir de las diferentes medidas de eficiencia no varía significativamente con la técnica de estimación ni con los upuestos de distribución. La evidencia empírica muestra que la clasificación de las medidas de eficiencia es similar, particularmente en la parte superior e inferior de la clasificación, donde se puede concentrar el interés del investigador (Kumbhakar y Lovell, 2000).
En el presente trabajo se usa la prueba sugerida por Schmidt y Sickles (1984) para determinar la mejor estimación de datos de panel, y, dado que no es posible seleccionar a priori el mejor supuesto de distribución para el término de ineficiencia, se estiman diferentes modelos y se analizan los cambios en los parámetros, para ver la sensibilidad a los supuestos realizados.
Especificación y descripción de las variables
Como se mencionó anteriormente, en el análisis empírico se utiliza una función de costos translogarítmica; el sector metalmecánico presenta un claro encadenamiento hacia adelante de los diferentes subsectores y, en tal sentido, la minimización en la estructura de costos es importante, optimizando el uso de los insumos requeridos en las diferentes etapas para la obtención de los productos ofrecidos. El análisis se realiza en términos de agregados industriales del sector en cada uno de los 12 departamentos que reportó información durante los años de referencia, incluyendo a Antioquia, Atlántico, Boyacá, Bolívar, Caldas, Cauca, Cundinamarca, Norte de Santander, Quindío, Risaralda, Santander y Valle del Cauca. Los datos requeridos en el proceso de estimación fueron obtenidos de la EAM, disponible en el DANE, y del sistema de información minero energético colombiano. Dado que son 12 departamentos y cada uno cuenta con 10 datos por año en cada variable, se observa que el número total en el panel de datos por año corresponde a 120 observaciones.
De acuerdo con las características del sector metalmecánico y siguiendo la Gráfica 1, los insumos que mayor impacto ejercen sobre la estructura de costos son el capital, la mano de obra y el consumo de energía eléctrica. Teniendo en cuenta lafunción de costos, se hace necesario incluir los precios de los factores, al igual que el valor de la producción generada a partir de dicha combinación. Así, la función de costos estará representada entonces por:
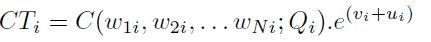 | [10] |
Donde C(.) es una función de costos no decreciente, linealmente homogénea y cóncava en precios, y 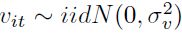 y
y 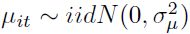 representan, respectivamente, el ruido estocástico y la ineficiencia. De igual forma, se debe considerar que al imponer las restricciones de homogeneidad de la ecuación (10), se normalizan todos los insumos, por un insumo seleccionado de manera aleatoria, así:
representan, respectivamente, el ruido estocástico y la ineficiencia. De igual forma, se debe considerar que al imponer las restricciones de homogeneidad de la ecuación (10), se normalizan todos los insumos, por un insumo seleccionado de manera aleatoria, así:
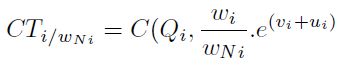 | [11] |
En particular, teniendo en cuenta lo planteado con respecto a la estructura de costos del sector metalmecánico en Colombia, la función será:
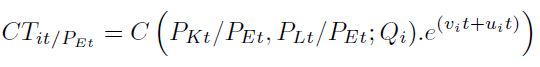 | [12] |
Siendo:
CTit: costo total en el departamento i en el periodo t.
PKt: costo del capital en el departamento i en el periodo. t
PLt: costo de la mano de obra del departamento i en el periodo t.
PEt: costo de la energía eléctrica del departamento i en el periodo t.
Qit: producción de la manufactura del departamento i en el periodo t.
vit: el término de error estocástico.
μit: el término que captura la ineficiencia en costos de producción.
Por otra parte, en cuanto a la forma funcional de la función de costos, Coelli y Perelman (2000) plantean que, idealmente, esta debería ser flexible, fácil de calcular y permitir la imposición de homogeneidad. Dado que la forma funcional translogarítmica satisface de manera adecuada dichos requisitos, para determinar el desempeño del sector metalmecánico en Colombia se estimará la siguiente función translogarítmica:
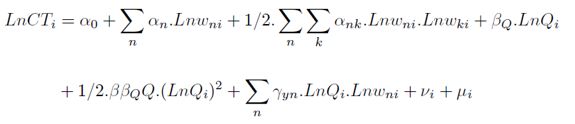 | [1] |
La descripción de las variables corresponde a la descrita en la ecuación (12), y, siguiendo a Coelli, Rao, O'Donell y Battese (2005), cada una de las variables se normaliza por su media a priori a la estimación. La función de costos representada en la ecuación (13) se estima usando el programa Frontier, versión 4.14, y el programa Stata.
La variable empleada para medir el producto del sector metalmecánico en Colombia, durante el periodo 1998-2007, es el total del valor agregado de los cuatro subsectores que lo componen en cada departamento, debido al encadenamiento hacia adelante señalado con anterioridad. De otro lado, teniendo en cuenta que los insumos que mayor impacto generan sobre la estructura de costos son la mano de obra, el capital y el consumo de energía eléctrica, se incluyen como regresores en la estimación el precio de estos insumos, es decir, el salario, la tasa de interés y el costo de la energía eléctrica, respectivamente. En el Cuadro 3 se presenta el resumen de las estadísticas descriptivas de las diferentes variables utilizadas en el modelo.
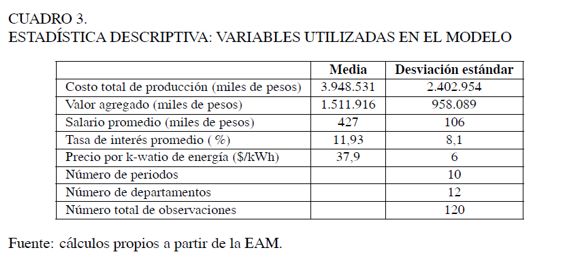
Por otra parte, los primeros desarrollos de las técnicas de frontera que utilizan datos de panel suponían que, aunque los niveles de eficiencia variaban a través de las firmas, eran constantes durante el tiempo. Sin embargo, si el análisis se realizaba para un periodo amplio, se podría estar dejando de lado información sobre el cambio en los niveles de eficiencia de las unidades de producción durante el periodo de análisis. Para suplir esta necesidad, Battese y Coelli (1992) establecen la posibilidad de estimar la eficacia a través del tiempo. Estos autores introducen a la estimación de corte transversal la posibilidad de estimar interceptos cambiantes, tanto para las unidades de producción como en el tiempo, así:
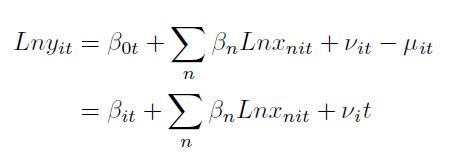 | [14] |
A partir de la ecuación (14) se obtienen tanto los estimadores de los parámetros que describen la estructura de producción como los estimadores de la eficiencia para cada firma. Considerando que el análisis empírico se efectúa para un periodo de 10 años, además de realizar las estimaciones con datos de panel asumiendo que la eficiencia
no varía en el tiempo, se elaboran las estimaciones suponiendo que hay un
cambio en el tiempo, de acuerdo a la parametrización de Battesse y Coelli (1992). El término de eficiencia es igual a 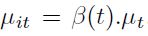 , donde
, donde 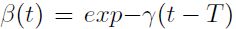 y γ es un parámetro adicional que debe ser estimado. Para seleccionar si es más apropiado un modelo con cambio de la eficiencia en el tiempo o no, se emplea la prueba de la razón de verosimilitud, la cual compara la bondad de ajuste a los datos de un modelo relativamente más complejo con uno más simple.
y γ es un parámetro adicional que debe ser estimado. Para seleccionar si es más apropiado un modelo con cambio de la eficiencia en el tiempo o no, se emplea la prueba de la razón de verosimilitud, la cual compara la bondad de ajuste a los datos de un modelo relativamente más complejo con uno más simple.
RESULTADOS EMPÍRICOS
En esta sección se presentan los resultados de la estimación de la frontera de costos translogarítmica descrita en la sección anterior (ecuación 10). Teniendo en cuenta que las observaciones del modelo consideran un panel de datos de 12 departamentos y 10 años, la frontera de costos se estima utilizando modelos de efectos fijos y efectos aleatorios. Para seleccionar cuál de los dos modelos es más apropiado se emplea la prueba de Hausman y la prueba Breush-Pagan. El modelo de efectos aleatorios se estima utilizando mínimos cuadrados generalizados (MCG) y métodos de máxima verosimilitud (MV). En las estimaciones de MV se utiliza la distribución de media normal y de normal truncada5.
Adicionalmente, teniendo en cuenta que durante el periodo de análisis se pudieron haber presentado cambios en la eficiencia del sector metalmecánico, se considera la parametrización de Battese y Coelli (1992). Para realizar comparaciones de los resultados de la eficiencia con y sin cambio de la eficiencia en el tiempo, se supone una distribución normal truncada, considerando que la parametrización de Battese y Coelli (1992) utiliza dicha distribución.
En el Cuadro 4 se presentan los resultados de las estimaciones de la función de costos translogarítmica. Dado que las variables están expresadas en logaritmos y reescaladas en unidades a sus medias, los coeficientes de primer orden pueden ser interpretados como elasticidades (Coelli, Rao, O'Donell y Battese, 2005). La prueba de Hausman y la prueba de Breush-Pagan (BP) apoyan los modelos de efectos aleatorios sobre el modelo de efectos fijos, considerando que el estadístico LM (12,82) es mayor que su valor crítico y que el de Hausman (0,33), el cual a su vez es menor que su valor crítico. Los modelos de efectos aleatorios fueron estimados utilizando MCG y métodos de máxima verosimilitud.
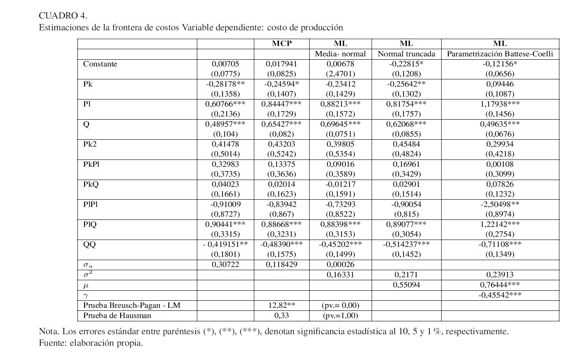
Estos suponen que el efecto específico individual capturado a partir del intercepto es aleatorio, es decir, que su naturaleza es estocástica, similar a la del término de perturbación o ruido estadístico. Las estimaciones que utilizan MV son generalmente más eficientes, ya que incluyen un supuesto de distribución que permite separar el componente de error entre la parte aleatoria y el término de ineficiencia.
Como ya se explicó, la parametrización de Battese y Coelli (1992) incluye un parámetro adicional γ, y presenta las propiedades: f(t) ≥ 0 y f(T) = 0. En este caso, Battese y Coelli (1992) suponen que ui también presenta una distribución normal truncada, es decir, 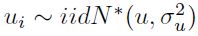 .
.
Resulta interesante observar que, tanto en el modelo de efectos fijos como en los modelos de efectos aleatorios estimados, utilizando MCG y métodos de MV con distribución de media normal (ML media-normal) y normal truncada (ML normal truncada), el precio del capital resulta inversamente proporcional al costo total de producción.
Este resultado podría indicar cierto grado de concentración de la actividad metalmecánica y, con ello, algún tipo de barrera de acceso al mercado. En efecto, al determinar el número de establecimientos industriales dedicados a la fabricación de productos del sector metalmecánico se encuentra que, durante 1998 y 2007, en promedio, cerca del 80% de ellos se concentra en Bogotá D.C., Antioquia y Valle del Cauca, como se observa en la Gráfica 3.
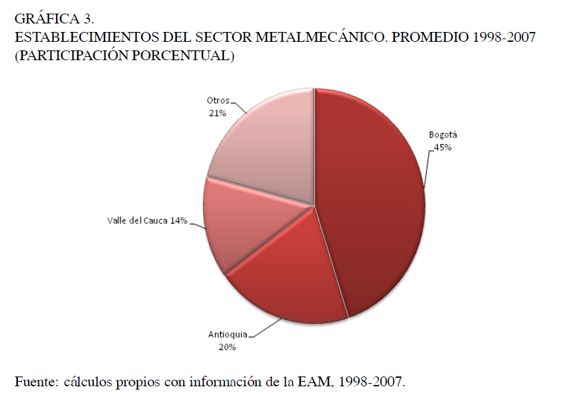
Siguiendo a Bain (1956), las barreras de entrada se pueden entender como aquella inversión de alto costo que permite el logro de mayores beneficios, sin estimular necesariamente el ingreso de nuevas empresas en el sector. El sostenimiento de estos beneficios y la concentración del mercado se pueden explicar a partir de las economías de escala, las ventajas absolutas en los costos de producción, las necesidades iniciales de capital que requiere el sector y la diferenciación del producto; factores que, de forma directa o indirecta, se evidencian en el sector metalmecánico colombiano y que requieren un mayor estudio en investigaciones futuras.
Sin embargo, en los modelos estimados, tanto de efectos fijos como de efectos aleatorios, el coeficiente de elasticidad del precio de capital no es estadísticamente significativo y resulta ser muy inferior al efecto evidenciado por el precio de la mano de obra y la producción, que explican en un 60% y 48%, respectivamente, las variaciones del costo total de producción del sector en el modelo de efectos fijos; mientras que en el modelo de efectos aleatorios, lo explican aproximadamente en un 85% y 65%, respectivamente. En este sentido, se observa una alta influencia de la mano de obra en los costos de producción. Se resalta que, a partir de la información de la EAM (1998-2007), en promedio el 44% del personal ocupado del sector metalmecánico se ubica en Bogotá D.C., el 22% en Antioquia, el 13% en el Valle del Cauca, y el 21% en el resto de los departamentos que reportan producción en dicho sector manufacturero.
De igual forma, en el Cuadro 4 se presentan los resultados siguiendo la parametrización de Battesse y Coelli (1992), y se encuentra que los coeficientes relacionados con el precio del capital cambian de forma importante, lo que podría sugerir que la utilización del capital ha tenido un gran impacto en la explicación de los costos del sector durante el periodo analizado. Este hecho se podría explicar a partir de diferentes incentivos, otorgados por el Gobierno nacional al sector metalmecánico en busca de mejores niveles de producción a menor costo.
Dadas las diferencias entre los modelos de frontera que no consideran cambios en la eficiencia durante el tiempo y los resultados a partir de la parametrización de Batesse y Coelli (1992), se realizó una prueba de la razón de verosimilitud para establecer el modelo que mejor se ajusta a los datos (Cuadro 5). Los resultados indican que la hipótesis nula Ho : γ = 0 es rechazada por los datos, por lo que se sugiere que el modelo de Battese y Coelli (1992) es el más adecuado y que, durante el periodo de análisis (1998-2007), se presentaron cambios significativos en la eficiencia de costos, con impacto sobre los niveles de eficiencia de las unidades de producción. Este resultado es consistente con el resultado encontrado para γ, el cual, como se observa en el Cuadro 4, resulta significativo.

Los resultados a favor de la parametrización de Batesse y Coelli sugieren que, durante el periodo de análisis, se registró en promedio un cambio significativo en los niveles de eficiencia de costos de las empresas del sector. Esta situación se puede explicar, como se mencionó anteriormente, por el desarrollo que tuvo el sector después de la apertura y las diferentes apuestas productivas en el marco de los "acuerdos de voluntades y decisiones entre el Gobierno nacional, las entidades territoriales, el sector privado, los representantes políticos y la sociedad civil, sobre las acciones estratégicas que debe realizar el país para mejorar su productividad y competitividad" (DNP, 2007, p. 7).
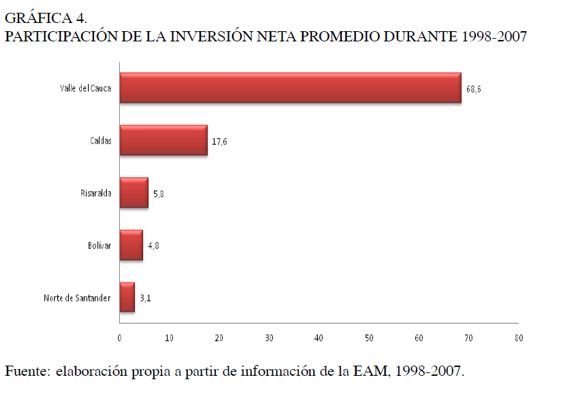
De otro lado, teniendo en cuenta que el capital se relaciona tanto con la inversión neta como con el total de los activos, es importante destacar que dentro de los 5 departamentos que presentaron valores positivos promedios en su inversión neta, el Valle del Cauca es el departamento que mayor esfuerzo ha realizado para incrementarla, pues su participación alcanza el 68%, seguido por Caldas y Risaralda, que alcanzaron el 17% y el 5%, respectivamente (véase Gráfico 4). Los departamentos de Caldas y Risaralda habían manifestado en el documento sectorial del DNP (2007) un claro interés por realizar una apuesta productiva en este sector industrial, incrementando la articulación entre producción y comercialización, y mejorando para ello la infraestructura vial y de servicios públicos existentes en su territorio.
Eficiencia en costos
De acuerdo con las pruebas de Hausman y de Breush-Pagan referenciadas en los resultados empíricos, se identifica que el modelo de efectos aleatorios es más apropiado que el modelo de efectos fijos6; por lo tanto, el análisis de la eficiencia en costos se realiza, por un lado, a partir del modelo de efectos aleatorios, el cual emplea una distribución normal truncada, obteniendo la eficiencia en cada departamento sin considerar cambios en el tiempo; por otro lado, a partir de la parametrización de Battesse y Coelli que, a diferencia del anterior, sí considera cambios en el tiempo. Los resultados se presentan en el Cuadro 6.
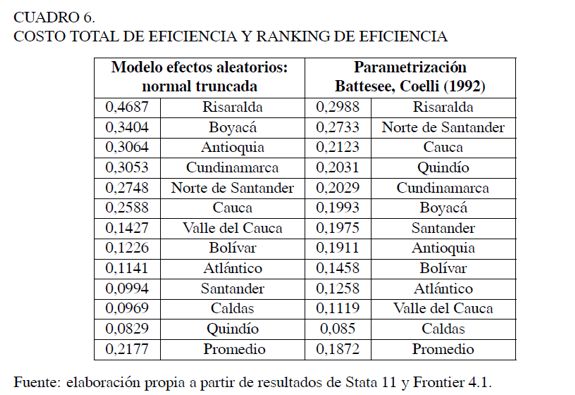
El ranking en la eficiencia del costo total de la producción metalmecánica en Colombia, durante el periodo 1998-2007, presenta algunas diferencias en los modelos analizados; cuando la eficiencia no varía en el tiempo, en promedio es cercana al 22%, y al considerar variaciones en el tiempo, es de alrededor del 19%. Adicionalmente, se observa una mayor variabilidad en el primer modelo, donde se registra una desviación estándar del 12,5%, mientras que en el segundo la desviación estándar alcanza el 6,2%. No obstante, bajo los dos modelos, Risaralda es el departamento con la mayor medida de eficiencia en costos, mientras que Caldas registra las menores medidas de eficiencia.
A partir de la razón de verosimilitud realizada en la sección anterior, se encuentra evidencia a favor del modelo de Battese y Coelli (1992), y, con ello, se favorece la hipótesis de que durante el periodo 1998-2007 hubo un cambio en la eficiencia en los 12 departamentos que reportaron producción en el sector metalmecánico, según los datos de la EAM, clasificación CIIU (revisión 2, de tres dígitos). La información de la eficiencia en costos de cada departamento y su variación en el tiempo se observa en la Gráfica 5. En todos los departamentos se contempla un aumento importante en los niveles de eficiencia durante el periodo analizado. Este resultado podría indicar evidencia de un aumento en la optimización de los recursos productivos en el tiempo, lo cual podría ser resultado de las políticas económicas que estimularon el cambio tecnológico en dicho sector.
En particular, los resultados indican que durante 1998 los niveles de eficiencia se ubican alrededor del 2 %, con una volatilidad del 6 %, lo que supone altos niveles de ineficiencia del sector metalmecánico a finales de los noventa. Este resultado puede reflejar la fuerte contracción de la demanda agregada observada durante 1999, año de la última crisis económica en Colombia, con caídas superiores al 4% de la producción nacional; en palabras de Silva (2003), el peor año en las últimas tres cuartas partes del siglo veinte, un periodo en el que las previsiones sobre crecimiento económico estuvieron muy distantes de la realidad.
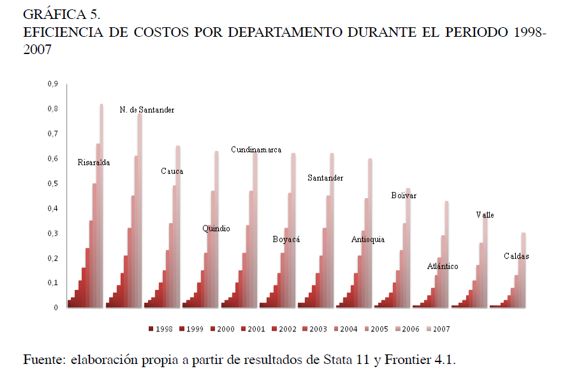
Una vez superada la crisis económica, específicamente a partir del 2001, en todos los departamentos se presenta una clara tendencia de mejoramiento en el comportamiento de la eficiencia en los costos. No obstante, se presenta que, en los diferentes años, Risaralda siempre es el departamento más eficiente, pasando de 3% en 1998 a 82% en 2007, seguido del departamento Norte de Santander, cuya eficiencia pasa de 2% a 78% durante el mismo periodo. Por el contrario, el departamento de Caldas registra los menores niveles de eficiencia, al pasar de 1% a 30% durante el mismo periodo (Cuadro 7).
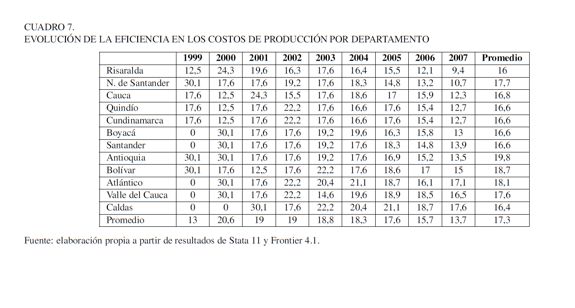
Es importante destacar que, si bien es cierto que Boyacá es el departamento que reporta una mayor producción en términos agregados del sector metalmecánico, en el ranking de eficiencia en costos de producción ocupa el sexto lugar a partir de la parametrización Battesee Coelli (1992), lo que implicaría que existen grandes posibilidades de incrementar los beneficios económicos en el sector, en la medida en que su eficiencia en costos solo alcanza el 20%; en una situación parecida se encuentran los departamentos de Antioquia y Valle del Cauca. En cuanto al departamento de Risaralda, el cual registra el primer lugar en el ranking de clasificación de eficiencia, se tiene que hasta el año 2003 fue el séptimo productor del sector. A partir de este año ha participado de manera más activa y se mantiene como el quinto departamento de mayor producción a nivel nacional.
Finalmente, teniendo en cuenta que la prueba de la razón de verosimilitud indica que durante el periodo de análisis la eficiencia de costos registró un cambio significativo, se calculó para cada departamento el cambio anual de la eficiencia con base en la siguiente fórmula: 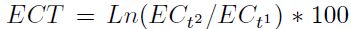 . Los resultados indican que durante el periodo la eficiencia mejoró en promedio el 17,3%. El año de mayor incremento fue el 2000, posterior a la crisis económica de 1999, y el departamento que en promedio mejoro más la eficiencia fue Antioquia (Cuadro 7).
. Los resultados indican que durante el periodo la eficiencia mejoró en promedio el 17,3%. El año de mayor incremento fue el 2000, posterior a la crisis económica de 1999, y el departamento que en promedio mejoro más la eficiencia fue Antioquia (Cuadro 7).
CONCLUSIONES
La estructura económica colombiana se inserta en la dinámica de internacionalización, dados los procesos de apertura comercial y de capitales adoptados por el país a partir de 1990. Sin embargo, solo hasta mediados del año 2004 se inicia la construcción de una agenda interna, promovida por el Consejo de Política Económica y Social (Conpes) mediante su documento n.o 3297, orientado a la coordinación, priorización y fomento de la productividad y la competitividad del país. A partir de las diferentes agendas departamentales, se identifican planes de mejoramiento de la productividad que finalmente llevan a que los productores de los distintos eslabones de la cadena productiva de la metalmecánica y la siderurgia -específicamente en los departamentos de Risaralda, Caldas y Atlántico- se comprometan con una mayor articulación entre la producción y la comercialización del sector, mejorando para ello tanto su infraestructura vial como la producción del sector metalmecánico.
Al observar la evolución del aporte que el sector metalmecánico hace a la producción industrial del país durante el periodo 2000-2007, se encuentra que esta pasó del 8,9% al 11,3%, con un mayor dinamismo en los departamentos de Cauca, Bolívar y Risaralda, donde las tasas de crecimiento promedio fueron 63,7%, 20,9% y 20,5%, respectivamente. Así mismo, se puede resaltar que los departamentos de Risaralda, Caldas y Atlántico realizaron una apuesta productiva por el sector metalmecánico, pero solo el primero de ellos muestra resultados que le favorecen en términos de una mayor producción.
Considerando la importancia del sector metalmecánico en la industria colombiana, el presente documento tiene como fin determinar el desempeño del sector a través de un análisis de eficiencia económica en sus costos de producción. En el análisis empírico se utilizan técnicas de frontera estocástica con una función de costos translogarítmica. Una de las ventajas de utilizar análisis de frontera con respecto a las técnicas econométricas tradicionales es que provee medidas específicas de eficiencia. El análisis se realiza para una muestra de 12 departamentos de Colombia, durante el periodo 1998-2007, con información de la EAM, según clasificación CIIU (revisión 2, de tres dígitos). Aunque existen diversos estudios del sectormetalmecánico en Colombia, el presente documento se constituye en el primero en estudiar la eficiencia del sector, utilizando técnicas de frontera estocástica.
La estimación de la frontera de costos, suponiendo una estructura translogarítmica, se efectuó con modelos panel de datos con efectos fijos y efectos aleatorios. Los resultados de las pruebas estadísticas indican que el modelo de efectos aleatorios es el más apropiado para explicar el comportamiento de la eficiencia en los costos de producción del sector metalmecánico.
El modelo de efectos aleatorios fue estimado desde mínimos cuadrados generalizados (MCG) y métodos de máxima verosimilitud (MV), suponiendo en el segundo caso una distribución de media normal y normal truncada; finalmente, con la parametrización de Battese y Coelli (1992), se identificó la presencia de cambios significativos en la eficiencia de costos del sector metalmecánico durante el periodo analizado.
Los resultados de las estimaciones, de acuerdo con los modelos de efectos fijos y de efectos aleatorios, indican una relación inversa entre el precio del capital y el costo total de producción, sugieren la existencia de cierto grado de concentración de la actividad metalmecánica y, con ello, algún tipo de barrera de acceso al mercado, teniendo en cuenta que cerca del 80% de los establecimientos dedicados a la producción del sector se encuentran en Bogotá D.C., Antioquia y Valle del Cauca; en otros términos, en caso de existir efectivamente barreras o restricciones de entrada, estas se explican por la inversión de alto costo requerida para el logro de mayores beneficios, sin estimular necesariamente el ingreso de nuevas empresas al sector. No obstante, el alcance del trabajo no permite realizar ningún tipode afirmación al respecto y resulta interesante que posteriores investigaciones se encarguen de documentar este hecho de manera más detallada.
Por otra parte, los resultados del modelo con la parametrización de Battesse y Coelli (1992) indican que los coeficientes relacionados con la variable precio del capital cambian de forma significativa, y sugieren con ello que la utilización del capital es importante en la explicación de los costos del sector. Es necesario señalar que la prueba de la razón de verosimilitud arroja evidencia en favor de este modelo, lo cual indica la presencia de cambio en la eficiencia del sector metalmecánico durante el periodo analizado. Este resultado se puede explicar debido al impacto de la crisis económica registrada en el país a finales de la década de los noventa, cuando las diferentes unidades de producción incluidas en el análisis registraron los niveles de eficiencia más bajos. Finalmente, se observa que el departamento que ha registrado los mayores niveles de eficiencia de costos es Risaralda, y los menores, Caldas.
NOTAS AL PIE
3 Excepto maquinaria y equipo (CIIU 381).
4 Este programa, que es especializado en la estimación de la frontera estocástica, fue desarrollado por Coelli (1996), y su versión 4.1 se encuentra disponible en: http://www.uq.edu.au/economics/cepa.
5 Los resultados de la distribución exponencial no se presentan debido a que el modelo no converge para el conjunto de información utilizada.
6 Si bien la especificación del modelo es igual, Yit = α+βXit+νi+μit, la diferencia radica en que el componente de error estadístico νi es constante y fijo en el tiempo para cada individuo, mientras que en el modelo de efectos aleatorios se comporta de manera aleatoria para cada individuo. Si bien el segundo modelo es más eficiente, presenta el inconveniente de ser menos consistente, es decir, se encuentra más sesgado.
REFERENCIAS BIBLIOGRÁFICAS
[1] Acevedo, M. C. y Ramírez, J. (2005). Diferencias regionales en la eficiencia técnica del sector de confecciones en Colombia: un análisis de fronteras estocásticas. Innovar, 15(26), 90-105.
[2] Aigner, D. J. y Chu, S. F (1968). On estimating the industry production function. American Economic Review, 52(4), 762-782.
[3] Aigner, D. J., Lovell, C. A. K. y Schmidt, P. J. (1977). Formulation and estimation of stochastic frontier production function models. Journal of Econometrics, 6, 21-37.
[4] Bain, J. (1956). Barriers to New Competition. Cambridge, MA: Harvard University Press.
[5] Barrientos, M., Tobón J. y Gutiérrez, A. (2009). Producción y eficiencia estocástica: una aplicación a la industria del calzado en Colombia. Lecturas de Economía, 70, 165-190.
[6] Battesse, G. & Coelli, T. J. (1988). Prediction of firm-level technical efficiencies with a generalized production functions and panel data. Journal of Econometrics, 38, 387-399.
[7] Battese, G. & Coelli, T. J. (1992). Frontier Production Functions, Technical Efficiency and Panel Data: With Application to Paddy Farmers in India. Journal of Productivity Analysis, 3, 53-169.
[8] Cavallé, C. (1975). El sector siderúrgico español. Pamplona: Ed. Eunsa; Confederación Empresarial Valenciana (1995).
[9] Coelli, T., Estache, A., Perelman, S. y Trujillo, L. (2003). A Primer on Efficiency Measurement for Utilities and Transport Regulators. Washington, D.C.: The World Bank.
[10] Coelli, T. J., Rao D. S., O´Donell, C. J. y Battese, G. E. (2005). An introduction to efficiency and productivity analysis. Boston: Kluwer Academic Publishers.
[11] Coelli, T. y Perelman, S. (2000). Technical efficiency of European railways: a distance function approach. Applied Economics, 32(15), 1967-76.
[12] Debreu, G. (1951). The coefficient of resource utilization. Econometrica, 19(3), 273-292.
[13] Departamento Nacional de Planeación (DNP). (2004). Agenda interna para la productividad y la competitividad (Documento Conpes 3297). Colombia: Consejo Nacional de Política Económica y Social.
[14] Departamento Nacional de Planeación (DNP). (2007). Agenda interna para la productividad y la competitividad (Documento Sectorial Metalmecánica y Siderurgia). Colombia: Consejo Nacional de Política Económica y Social.
[15] Díaz, M. A. y Sánchez, R (2008). Firm size and productivity in Spain: a stochastic frontier analysis. Small Business Economics, 30(3), 315-323.
[16] Farrell, M.J. (1957). The Measurement of Productive Efficiency. Journal of the Royal Statistical Society, Series A, CXX, Part 3, 253-290.
[17] Greene, W. (1993). The econometric approach to efficiency analysis. En Lovell K. y Schmidt S. (Eds.), The Measurement of Productive Efficiency: Techniques and Applications (pp. 68-119). Oxford University Press.
[18] Jondrow, J. et al. (1982). On the estimation of technical inefficiency in the stochastic in the stochastic frontier production function model. Journal of Econometrics, 19, 233-238.
[19] Koopmans, T. C. (1951). An Analysis of Production as an Efficient Combination of Activities. En T. C. Koopmans (Ed.), Activity Analysis of Production and Allocation (Cowles Commission for Research in Economics, Monograph 13). New York: John- Wiley and Sons, Inc.
[20] Kumbhakar, S. y Lovell K. (2000). Stochastic Frontier Analysis. Cambridge: Cambridge University Press.
[21] Lovell, K. (1993). Production frontiers and productive efficiency. En Lovell K. and Schmidt S. (Eds.), The Measurement of Productive Efficiency: Techniques and Applications (pp. 3-67). Oxford University Press.
[22] Managi, S., Opaluch, J y Grigalunas, T. (2006). Stochastic frontier analysis of total factor productivity in the offshore oil and gas industry. Ecological Economics, 60(1), 204-215.
[23] Meeusen,W. y Van Den Broeck, J. (1977). Efficiency estimation fromCobb-Douglas production functions with composed error. International Economic Review, 18(2), 435-444.
[24] Melo, L. (2005). Impacto de la descentralización fiscal sobre la educación pública en Colombia (Borradores de Economía, 350). Bogotá: Banco de la República.
[25] Melo, L. y Espinosa, N. (2005). Ineficiencia en la distribución de energía eléctrica: una aplicación de las funciones de distancia estocástica. Ensayos sobre Política Económica, 49, 88-132.
[26] Schmidt, P. y Sickles, R. (1984). Production frontier and panel data. Journal of Business and Economic Statistics, 4, 367-374.
[27] Silva, J. (2003, septiembre). Colombia: crisis del crecimiento económico. Expresión en el comportamiento de la oferta final, 1990-2002. Economía y Desarrollo, 2(2), 20-34.
[28] Solow, R. M. (1957). Technical Change and the Aggregate Production Function. The Review of Economics and Statistics, 39(3), 312-320.
[29] Tyler, W. y Fei, L. (1979). On Estimating Stochastic Frontier Production Functions and Average Efficiency: An Empirical Analysis with Columbian Micro Data. The Review of Economics and Statistics, 61(3), 436-438.
[30] Unctad. (2008). Handbook of Statistics. New York and Geneva: United Nations Publication.