Income Inequality and Economic Growth: New Evidence From Latin America
Desigualdad en la distribución del ingreso y crecimiento económico: nueva evidencia de latinoamérica.
Inégalité dans la distribution du revenu et croissance économique : nouvel exemple d'amérique latine.
Desigualdade na distribuição da renda e crescimento econômico: nova evidência da américa latina.
Fernando Delbiancoa
Carlos Dabúsb
María Ángeles Caraballoc
a Master of Econometrics, Universidad Nacional del Sur and IIESS, 12 de Octubre 1198. 7mo Piso. Bahía Blanca, Argentina. Email:fernando.delbianco@uns.edu.ar
b Doctor of Economics, CONICET and Universidad Nacional del Sur. 12 de Octubre 1198. 7mo Piso. Bahía Blanca, Argentina. Email: cdabus@criba.edu.ar
c Doctor of Economics, Universidad de Sevilla, Facultad de Ciencias Económicas y Empresariales, Seville. Spain. Email: mcaraba@us.es
The authors would like to thank the two anonymous referees for their valuable comments. The usual disclaimer applies.
Abstract
This paper explores the relationship between the inequality of income distribution and the economic growth of 20 Latin American and Caribbean countries during the 1980-2010 period. The study shows that the features of this relationship depend on the income level. In general, inequality is harmful to economic growth. However, when it comes to the upper tail of the richer countries' income distribution, higher inequality encourages economic growth and the relation becomes positive. Thus, contrary to the economic policy recommendations for the richer countries, our evidence suggests that progressive redistributive policies in favor of poorer layers of population promote economic growth in lower income economies.
Keywords: Income inequality, economic growth, level of development, developing economies, Latin America.
JEL: O11, O15, O47, C23.
Resumen
En este artículo se estudia la relación entre desigualdad del ingreso y crecimiento para 20 economías de América Latina y el Caribe, para el periodo 1980-2010. Los resultados muestran que la relación entre desigualdad e ingreso depende fuertemente del nivel de ingreso que un país presente. En general, la desigualdad afecta de manera negativa al crecimiento. En cambio, para los países más ricos, mayor desigualdad determina mayor crecimiento. Por ende, las recomendaciones de política que surgen de los resultados de este artículo serían aquellas con objetivo de reforzar las políticas redistributivas progresivas en los países de menor ingreso.
Palabras clave: desigualdad del ingreso, crecimiento económico, economías en desarrollo, Latinoamérica.
JEL: O11, O15, O47, C23.
Résumé
Dans cet article nous étudions la relation entre l'inégalité du revenu et la croissance dans 20 économies d'Amérique Latine et des Caraïbes pour la période 1980-2010. Les résultats montrent que la relation entre l'inégalité et le revenu dépend fortement du niveau de revenu de chaque pays. En général, l'inégalité affecte négativement la croissance. Par contre, pour les pays plus riches, plus d'inégalité représente plus de croissance. Par conséquent, les recommandations politiques qui dérivent des résultats de cet article seraient celles ayant pour objectif de renforcer les programmes de redistribution progressive dans les pays ayant les plus bas revenus.
Mots-clés : Inégalité du revenu, croissance économique, économies en développement, Amérique Latine.
JEL : O11, O15, O47, C23.
Resumo
Neste artigo, é estudada a relação entre desigualdade de renda e crescimento para 20 economias da América Latina e o Caribe, para o período 1980-2010. Os resultados mostram que a relação entre desigualdade e renda depende muito do nível de renda que um país apresentar. Em geral, a desigualdade afeta de maneira negativa o crescimento. Em compensação, para os paíes mais ricos, maior desigualdade determina maior crescimento. Portanto, as recomendações de política que surgem dos resultados deste artigo seriam aquelas com o objetivo de reforçar as políticas redistributivas progressivas nos países de menor renda.
Palavras-chave: Desigualdade da renda, crescimento econômico, economias em desenvolvimento, América Latina.
JEL: O11, O15, O47, C23.
Este artículo fue recibido el 7 de octubre de 2013, ajustado el 10 de marzo de 2014 y su publicación aprobada el 11 de marzo de 2014.
INTRODUCTION
The relationship between inequality and economic growth has been widely discussed in the literature. Since the seminal work of Kuznets (1955), and after the publication of the database on inequality by Deininger and Squire (1996), there has been growing evidence regarding the influence of income inequality on economic performance. However, some issues remain controversial, such as causality and the appropriate inequality measures. This lack of consensus can be explained mainly by the mixed results obtained in terms of how inequality affects growth, both theoretically and empirically. The theoretical discussion is twofold: the classical and the "political economy" approaches. The former argues that the saving rate increases with wealth. Therefore, given that inequality increases the income of the richer population, who have higher saving rates, this approach concludes that inequality encourages the accumulation of capital and, therefore, economic growth.
In contrast, for the "political economy" approach, increasing inequality leads to greater social pressure towards distribution policies. These policies create distortions, which negatively affect the accumulation of physical and human capital, and then economic growth. The intuition is that incentives for such an accumulation are based on the private returns appropriation, but this may be hampered in societies with high inequality and a distributive conflict, which reduce investment and growth. In turn, a greater inequality gives rise to imperfections in the credit market and, therefore, credit-constraints on human capital accumulation (Galor & Moav, 2004). Thus, in less developed economies-which in general present higher inequality levels-credit constraints should discourage human capital accumulation and, once again, economic growth.
Both approaches find support in the empirical literature. For example, Partridge (1997), Li and Zou (1998) and Forbes (2000), among others, present evidence on the beneficial effects of inequality on growth. In contrast, Persson and Tabellini (1994) and Deininger and Squire (1998) show that inequality is detrimental to growth. More recently, these conflicting results seem to be explained by nonlinearities in the inequality-growth relationship (Barro, 2000; Banerjee & Duflo,2003; Chen, 2003; Lin, Huang & Weng, 2006). In particular, Lin et al. apply a nonlinear estimation using the initial real income as a threshold variable. They find that an increase in inequality is harmful to economic growth in low income countries, but beneficial in high income economies.
On the other hand and historically, Latin America is known for having the largest income inequalities, along with strong sociopolitical and economic instability. Over the past few decades, this region has suffered recurrent and deep crises, which have led to a worsening of income distribution (see Gasparini & Lustig, 2011). In addition, Latin America has shown highly-cyclical economic developments without a clear growth trend and a poor long-term economic performance, particularly when compared with other emerging economies. Thus, the role of inequality in this region deserves particular attention. In this sense, in order to contribute with additional evidence on this topic, our goal is to study the "inequalityeconomic growth" relationship for Latin America during the 1980-2010 period. The hypothesis is that income inequality differently affects rich and poor countries, as well as the top end of the income distribution. Following Voitchovsky (2005), Lin, Huang, Kimz and Chih-ChuanYeh (2009) and Stewart and Moslares (2012), we use the Gini coefficient as a general level of inequality, and the share of the top ten percent of the richest population. In turn, to capture potentially differential effects of inequality, we include pondered variables between levels of income (grouping countries by cluster analysis) and measures of inequality in the estimations. Our results show that, in general, inequality is harmful for economic growth, but the relationship between both variables becomes positive for the richest populations of higher income countries.
The paper is organized as follows. First the two main theoretical approaches to the relationship "economic growth-inequality" in different income levels is discussed. Then the data set and variables is presented, then the model specification and empirical results are shown. Finally we conclude.
THEORETICAL AND EMPIRICAL BACKGROUND
The relationship between income inequality and economic growth has emerged as one of the major fields of research in economics. Nonetheless, the vast literature does not provide a unified consensus. Basically, two main approaches can be distinguished. The first is the classical theory, which defines a positive correlation between inequality and growth (see, for example, Stiglitz, 1969). Such a positive correlation is due to the assumption that the savings rate is higher for the rich than it is for the poor. Thus, increasing inequalities raise aggregate savings, investment and, in turn, promote economic growth. Moreover, this argument can be useful in explaining the divergence in the growth path of countries with similar initial conditions, like Argentina and Australia, whereby while for the former, savings resulted in a flight of capital, the latter channeled them into investment.
Secondly, in contrast to the classical view, the "political economy" approach suggests that inequality is detrimental to growth through different channels such as rent-seeking activities, social instability or credit market imperfections1. The rentseeking models point out that inequalities encourage the disadvantaged population to become involved in rent-seeking activities (Alesina & Perotti, 1994). These take away wealth from the economy and damage productivity and, therefore, growth. Alesina and Perotti (1996) highlight the relevance of the negative implications for growth brought about by the social and political instability, in turn, brought about by inequality. They point out that inequality can lead to social unrest. This shortens the duration of the governments in power, which, in order to maximize their "intertemporal utility", reduce the time horizon of their economic plans. More precisely, governments become more inclined to prioritize the current consumption over investment, reducing the long-term growth. Finally, Galor and Zeira (1993) focused on credit market imperfections. They pointed out that inequality reduces investments in human capital and, assuming that credit constraints are binding, higher inequality reduces growth.
More recently, Woo (2011) introduced fiscal policy volatility as a new channel to explain the negative link between inequality and growth. This is defined as the excessive discretionary changes in fiscal policy that take place for reasons other than smoothing out output fluctuations or responding to macroeconomic conditions.
In a theoretical paper, Galor and Moav (2004) provided a unified theory that combines both contradictory approaches. In their model, the relationship between inequalities in the distribution of income and growth depends on a country's stage of development. They stated that inequalities and growth are positively correlated at earlier stages, due to the main role played by physical capital accumulation in economic growth. In this sense, inequality helps development by channeling resources towards individuals with a higher marginal propensity to save. In later stages of development, the "credit market imperfection" approach is more relevant because human capital turns into the driving force, implying that the relationship between inequalities and growth becomes negative. As the development continues, the significance of both approaches vanishes, and then the effect of inequality on growth disappears. Chambers and Krause (2010) test this model for 54 countries using semiparametric techniques and find evidence supporting the theory proposed by Galor and Moav (2004). Similarly, Martínez (2013) finds support for this hypothesis using data for 1044 Colombian municipalities between 2005 and 2009.
De Dominicis, Floraxnn and Groot (2008) performed a meta-analysis for 37 works published between 1991 and 2006 in which inequality is measured by the Gini Index2. They conclude that studies based on cross-country regressions report a negative and significant relationship between initial income inequality and growth. However, this result is refuted when panel data models are used. These models find evidence of a positive and significant impact of inequality on growth that weakens when the system GMM (Generalized Method of Moments) estimator is adopted. In fact, Malinen (2013), using an alternative measure of income distribution and GMM estimation, finds evidence of a negative relationship in a sample of 70 countries (OECD and non-OECD) for the 1965-2000 period. Meanwhile, Dominicis et al. (2008) state that the results may also be affected by the duration of the study. The longer the period, the lower the magnitude of the coefficients found in the studies. This result supports the hypothesis that the underlying mechanisms of the relationship between inequality and economic growth works differently in the short and in the long run.
In addition, an increasing body of the empirical literature concludes that the impact of inequality on growth can be either positive or negative, depending on the different scenarios considered or the properties of the distribution of income. For example, Partridge (2005) shows that middle-class inequality share and overall inequality are positively related to long-run growth, while the linkage is not clear when considering short-run effects. However, the short-run income-distribution response is less clear. Fallah and Partridge (2007) find for US data during the 1990s, that the inequality-growth nexus is positive in the metropolitan areas and negative in the non-metropolitan areas. Similar results for Indian data for the 1965-2008 period are found by Tiwari, Shahbaz and Islam (2013). Interestingly, Bjornskov (2008) finds that the positive sign holds under rightwing governments and the negative sign under leftwing governments, while Atolia, Chatterjee and Turnovsky (2012) show that the nature of the productivity growth path plays a key role in explaining the growth-inequality relationship.
Moreover, Banerjee and Duflo (2003) state that higher inequality enhances (reduces) growth in more (less) egalitarian societies. Lin et al. (2009) show for a pool of 82 countries that a higher inequality is harmful for economic growth in low-income countries, but favorable in high-income ones. A similar result is achieved by Shin (2012) from a theoretical point of view. He presents a stochastic optimal growth model composed of heterogeneous agents who face a progressive tax system. In such a model, higher inequality can slow down growth in the early stages of development and can encourage growth in a near steady state. In turn, Voitchovsky (2005), focuses on the properties of the income distribution; in particular, she analyzes the influence of the shape of income distribution on economic growth for a panel of 25 countries, and claims that inequality within a country is positively correlated to growth at the top quartiles of the distribution, but negatively linked at the lower end of the distribution.
It is worth noting that both cross-country regressions and panel data models present limitations. As regards cross-country regressions, one of the criticisms is the causality and the endogeneity problem. Another methodological problem is the failure of cross-country regressions to take into account the specific characteristics of each country. Given that this method assumes a common economic structure across countries, the "omitted-variables problem" could arise. This problem is only partially solved by the homogeneous panel estimators commonly used by the inequality literature. These estimators control for country-specific omitted variables, but not for the country specific slope coefficients, and, if this is the case, the estimates of the average values of the parameters are inconsistent3.
In order to overcome these problems, Herzer and Vollmer (2012) use heterogeneous panel cointegration techniques to analyze the long-run effect of income inequality on income per capita and, thus, on long-run growth. They employ data from 46 developed and developing countries for the 1970-1995 period. These authors find a negative effect of inequality on income, both for the sample as a whole and for groups within the sample. Likewise, Abida and Sghaier (2012) apply panel cointegration methods to examine the income-inequality relationship for 4 countries in North Africa (Tunisia, Algeria, Morocco and Egypt) over the 1970-2007 period. They show that the long-run growth elasticity of income inequality is negative and significant. Malinen (2012) uses an unbalanced panel of 53 countries and concludes that there is a long-run equilibrium relationship between growth and inequality, and that this relationship is negative in developed economies.
Finally, Stewart and Moslares (2012) also show that income inequality affects growth negatively. They perform their work analyzing Indian states for the 1980-2010 period, and conclude that regional Gini coefficients affects the growth rate negatively, using the literacy rate and the coefficient of variation of the growth rate as control variables.
In short, the evidence is not conclusive, and the debate on the "income inequality-economic growth" relationship still stands; some results depend notably on the econometric method, the data and the sample of countries4. In this study, we explore the effect of inequality among different per capita income for 20 Latin American and Caribbean countries, and at different parts of the income distribution for sets of similar income countries.
DATA AND SUMMARY STATISTI CS
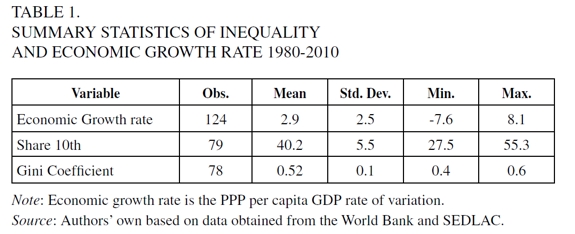
Our analysis of the relationship between inequality and growth includes data for the growth rate of the Gross Domestic Product (GDP), the ratio of investment to GDP, the net enrollment ratio in secondary schools as a proxy for education, the sum of exports plus imports to GDP as a measure for openness, the population growth and the Gini coefficient. All of them were obtained from the World Bank Data Set. Given the data availability, these variables are five-year averages. The 10% share of the richest population data was top ten income distribution provided by the SEDLAC.
Table 1 presents the summary statistics for growth and inequality variables for the whole sample used for the estimations, and Table 2 shows both the evolution of the growth and inequality average, and their minimal and maximum values for each period.
As we can see in both Tables, there is a relatively low growth and a high inequality level, in particular with respect to the most dynamic Asian emerging economies. Similarly, over the last decades, there has been a higher growth rate, but with vastly changing values across periods. This indicates a high volatility in the economies of the region.

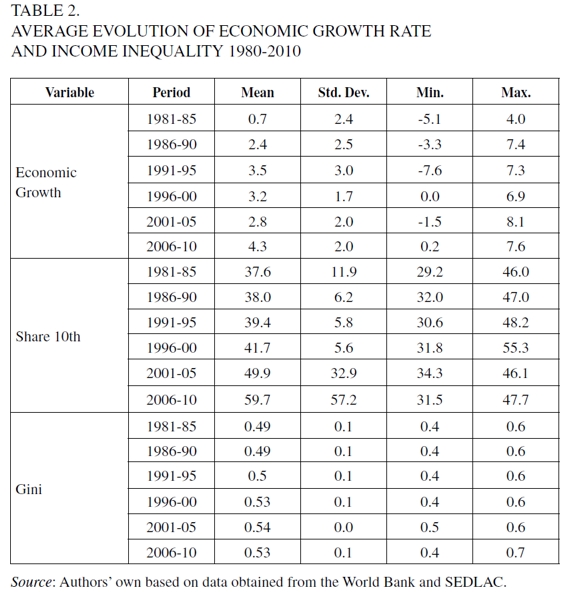
In relation to the measures of inequality, the average value of the Gini coefficient is in general above 0.50, and approximately 40% of the income is concentrated in the richest 10% of the population. This evidence is consistent with that presented in Gasparini and Lustig (2011), which illustrates that the region has the highest level of global inequality, and, similarly to the rest of the world, inequality presents few changes over time.
The estimations have been carried out for the sample as a whole and for two subgroups within it: Poorer and richer countries. In order to classify the countries, we used a k-means clustering method and the analysis was restricted to the two subgroups of high and low income we wanted to obtain. The similarity/dissimilarity measure was Euclidean and the stopping rule applied was the Calínski and Harabasz pseudo-F index. Both clusters accounted for about 70% of the variability in the income per capita. Once we applied the clustering, the countries were grouped into two sets of lower and higher incomes. Table 3 shows the results.

Table 3 indicates that income and economic growth are higher, and inequality is lower in the set of richer countries. In turn, this evidence suggests that inequality shows very high values compared to the rest of the world, even in the group of countries with less inequality (Gasparini & Lustig, 2011). Also, the fact that the higher-income countries group presents a higher average growth than the poorer set is consistent with the lack of convergence in the region found by Dabús and Zinni (2005); González, Dabús and Monterubbianesi (2013) for Latin America.
MODEL SPECIFICATION AND EMPIRICAL RESULTS
Model Specification
As is usual in this kind of literature, the dependent variable is economic growth. The explanatory variables are the control and the inequality variables. As far as the control variables are concerned, we have included those found as robust by Levine and Renelt (1992), i.e., the initial per capita income, the investment/GDP ratio, education, openness and population growth. As regards the inequality variables, we have used the Gini coefficient and the share of the richest 10% of the population. Besides this, in a second specification, we pondered these variables, and used them as an interaction between the level of income (high or low, dividing these groups with cluster analysis) and the inequality variables. These capture whether the inequality affects the tails of the income differently as mentioned in the discussion. Thus, the 5-year panel data growth model implies the following expressions,
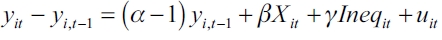 | [1] |
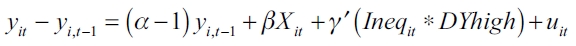 | [2] |
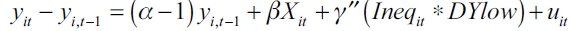 | [3] |
where yit is the economic growth of the country i in period t, Xit denotes the whole set of control variables proposed by Levine and Renelt (1992) mentioned above, Ineqit is the inequality measure, and DYhigh and DYhigh are dummies indicating whether the country belongs to the rich or the poor group (accordingly to the cluster division). Finally, uit is the error term and α, β and γ are the set of parameters to be estimated.
Our model estimation is based on the notion of the long-term steady-state income level. The intuition is that shifts in the independent variables will lead both to shortterm effects on growth and a long-term influence on the level of income per capita. Thus, a permanent change in income inequality will influence the growth rate in the short term, but this change will have only transitory effects on the growth rate. According to Voitchovsky (2005), the adjustment process to the newer long term steady-state can be a process which takes more than five years5, so that many lags (at least two, to control for a smooth decade adjustment) should be added to the specification. However, we include only one lag because of the inequality data availability. The estimations are carried out by means of a dynamic panel model, using the GMM with the Arellano and Bond (AB) specification. This is applied in this context of panel data with lagged values of some variables because the use of standard panel techniques (or a simple OLS analysis) will lead us to biased results6. The inclusion of first differences allows the removal of the unobserved time invariant individual effects, while the use of instrumental variables reduces potential endogeneity problems. In this sense, the instruments are the growth and Gini lagged values, and dummies indicating the five-year period (q1 to q5 - the last 5-year period was the base dummy), and the error term specification is robust.
A possible problem that can arise in the persistence of inequality is the low variabilityof the Gini coefficient variable. However, although inequality has been high in the region, it has suffered changes during the period under study. This allows us to assume that the variable presents the variability required in this type of analysis.
As a measure of goodness of fit we use the Sargan test (for over-identifying restrictions). It has a null hypothesis of "the instruments as a group are exogenous", based on the observation that the residuals should be uncorrelated to the set of exogenous variables if the instruments are actually exogenous. If the estimation is robust, the test is also known as the Hansen J statistic. In all AB specifications of the model shown in Table 4, the p-values obtained by Hansen–Sargan tests were above 0.10.
We made the specification as an AB model, and not a GMM system-that is, a Blundell and Bond (BB) estimator-because we tried to maintain the "parsimonious principle" in the estimation. The reason for doing so is the relatively small database used. With the level and differentiated instruments that a BB estimator requires, the degrees of freedom are fewer. Even so, if we estimate a BB case, the p-value obtained by applying the Sargan test is higher than 5%.
Empirical Results
This section presents the results of the estimations in Table 4, where AB denotes the Arellano and Bond estimator. Column 1 includes the control and inequality variables. Columns 2 to 5 add the dummies of interaction terms of higher and lower income countries with the 10% share of the richest and the Gini coefficient, respectively. The result of the Sargan test can be observed at the bottom of Table 4.
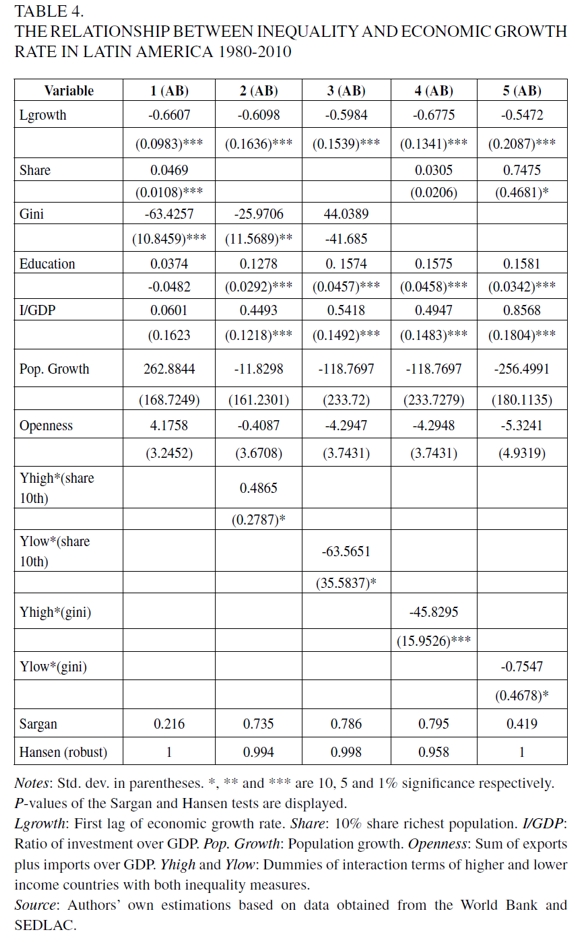
In relation to the control variables, the results show that investment, education and the lags of the dependent variable are significant and have the expected sign, while the population growth rate and openness coefficient are not significant. In turn, in most cases, the whole measure of inequality - i.e., the Gini coefficient - is harmful to economic growth, particularly in lower income countries. On the other hand, the 10% share of the richest, positively affects the economic growth. Moreover, estimations of Columns 3 and 5 show that in low levels of income, both the Gini coefficient and the 10% share of the richest are detrimental to economic growth. Hence, at lower income levels the results are compatible with the "political economy" approach, which sustains that higher inequality promotes social unrest. This is detrimental to investment and then to long-run economic growth. The intuition is that at lower stages of development, the problem of subsistence is more critical. This encourages distributive pressures, and, later, sociopolitical instability. Therefore, social conditions of medium-low income countries of Latin America seem to create an adverse environment to investment and economic growth. In those countries, an increase in inequality implies that there will be groups that do not meet their basic needs, while others are increasingly enriched in relation to the lower income groups. This could cause sociopolitical instability and harms incentives to investment and, in turn, economic growth, as explained above.
In contrast, the fact that the 10% share of the richest population in higher income countries encourages economic growth concurs with the classical view. In these cases, the subsistence difficulties of poorer countries should be resolved, resulting in a more favorable environment for high income sectors. These are supposed to channel savings into investment to promote economic growth.
In short, our evidence suggests that the income level matters: our results show that inequality does not impact all income distributions in the same way. In particular, inequality favors economic growth in the case of the richest 10% of the higher income countries. In this sense, the classical theory seems to be adequate to explain the case of the 10% share of the population of the richest Latin-American countries. Meanwhile, for the rest of the income distribution spectrum, our evidence is compatible with the "political economy" approach, in particular when considering the negative effect of the global inequality measure-i.e., the Gini coefficient-on economic growth. In this sense, the results suggest that social unrest associated with income inequality is relevant to discourage investment and economic growth only in poorer countries.
CONCLUSIONS
In this paper, we have studied the "inequality-economic growth" relationship for 20 Latin American and Caribbean countries during the 1980-2010 period. The evidence is "nearly eclectic". The relationship between inequality and economic growth depends heavily on the level of income. This suggests that the stage of development of each country matters for the analysis of the economic growth determinants. The intuition could be that the socio-economic environment of poor countries, and in particular of lower income social classes, could foster a climate of political instability, which poses the need for progressive redistribution. Meanwhile, at a higher income level the negative effects of inequality are mitigated. This makes room for policies promoting saving and investment by the richest groups that foster economic growth. In this sense, our evidence shows that inequality is generally harmful for economic growth. Such a result supports the "political economy" approach, as according to the results found by Malinen (2013) both for developed and developing countries. In turn, our evidence indicates that in the upper tail of the richer countries' income distribution, the results are rather different: here higher inequality promotes economic growth, so that the relationship becomes positive. Therefore, our findings confirm those found by Voitchovsky (2005) for 25 countries with a per capita income similar to or higher than that of the richer countries in our sample. In this sense, redistributive economic policies should be especially focused on those at the bottom of the income distribution. Here, the relative improvement of the poorer population must play a key role in improving economic development.
Finally, following are a number of interesting possible extensions to this work. One of them is to check the robustness of the results using alternative inequality measures. Further research should include the non-linear estimation, as well as the inclusion of thresholds of the income per capita. This could yield changes in the features of the "inequality-economic growth" relationship at different income levels. This should be helpful for a deeper understanding of the role of the true shape of such a relationship, as well as the underlying mechanisms throughout the income distribution. Finally, in order to have a broader understanding of the problem, an interesting line of research would be a comparative study of the "inequality- economic growth" relationship between developed and developing countries. This should allow us to reach a broader understanding of the phenomenon among clear-cut economic and institutional environments and, in particular, to find out the relevance of the classical and political economy approach at different stages of development.
FOOTNOTES
1 A related approach is employed for Jiménez (2006) for the Latin American countries.
2 It is worth noting that the Gini Index of Deininger and Squire (1996) has attracted serious criticism, concerning its consistency and accuracy (Atkinson & Brandolini, 2001; Galbraith & Kum, 2006). If the values of Deininger and Squire's Gini index are flawed, then the majority of the econometric studies on the topic are subject to errors.
3 See Pesaran and Smith (1995) for an explanation of this technique.
4 In particular, the estimation of income group elasticity in panel data with parametric methods requires some group-specific constants to be added to the estimation: This may cause the inference to be conditional toward the countries in the sample.
5 Moreover, Barro (2000) points out that to reach a new steady state can take a long time, so the 'short-term' effects on growth can be quite enduring.
6 The bias can be due to the correlation between the explanatory variables, the lagged term, and the error term (specifically the individual effects) once the lagged specification is selected.
REFERENCES
[1] Abida, Z., & Sghaier, I. (2012). Economic growth and income inequality: Empirical evidence from North African countries. Zagreb International Review of Economics and Business, 15(2), 29-44.
[2] Alesina, A., & Perotti, R. (1994). The political economy of growth: A critical survey of the recent literature. The World Bank Economic Review, 8(3), 351-371.
[3] Alesina, A., & Perotti, R. (1996). Income distribution, political instability, and investment. European Economic Review, 40(6), 1203-1228.
[4] Atkinson, A., & Brandolini, A. (2001). Promise and pitfalls in the use of 'secondary' datasets: Income inequality in OECD countries as a case study. Journal of Economic Literature, 39(3), 771-99.
[5] Atolia, M., Chatterjee, S., & Turnovsky, S. J. (2012). Growth and inequality: Dependence on the time path of productivity increases (and other structural changes). Journal of Economic Dynamics & Control, 36(3) 331-348.
[6] Barro, R. J. (2000). Inequality and growth in a panel of countries. Journal of Economic Growth, 5, 5-32.
[7] Barnejee, A. V., & Duflo, E. (2003). Inequality and growth: What can the data say? Journal of Economic Growth, 8, 267-99.
[8] Fallah, B., & Partridge, M. (2007). The elusive inequality-economic growth relationship: Are there differences between cities and the countryside? Annals of Regional Science, Springer, 41(2), 375-400.
[9] Bjornskov, C. (2008). The growth-inequality association: Government ideology matters. Journal of Development Economics, 87, 300-308.
[10] Chambers, D., & Krause, A. (2010). Is the relationship between inequality and growth affected by physical and human capital accumulation? Journal of Economic Inequality, 8 (2), 153-172.
[11] Chen, B-L. (2003). An inverted-U relationship between inequality and long-run growth. Economic Letters, 78(2), 205-212.
[12] Dabús, C., & Zinni, B. (2005). No convergencia en Latinoamérica. Anales de la XL Reunión Anual de la AAEP, November 2005.
[13] Dominicis, L., Floraxnn, R., & Groot, H. (2008). A meta-analysis on the relationship between income inequality and economic growth. Scottish Journal of Political Economy, 55(5), 654-682.
[14] Deininger, K., & Squire, L. (1996). A new data set measuring income inequality. World Bank Economic Review, 10(3), 563-91.
[15] Deininger, K., & Squire, L. (1998). New ways of looking at old issues: Inequality and growth. Journal of Development Economics, 57, 259-87.
[16] Forbes, K. J. (2000). A reassessment of the relationship between inequality and growth. American Economic Review, 9(4), 869-87.
[17] Galbraith, J., & Kum, H. (2006). Estimating the inequality of household incomes: A statistical approach to the creation of a dense and consistent global data set (Working Paper 22). UTIP.
[18] Galor, O., & Zeira, J. (1993). Income distribution and macroeconomics. Review of Economic Studies, 60(1), 35-52.
[19] Galor, O., & Moav, O. (2004). From physical to human capital accumulation: Inequality and the process of development. Review of Economic Studies, 71, 1001-26.
[20] Gasparini, L., & Lustig, N. (2011). The rise and fall of income inequality in Latin America (Working Paper 0118). CEDLAS, Universidad Nacional de La Plata.
[21] González, G., Dabús, C., & Monterubbianesi, P. (2013). Phases of convergence in Latin America: The technological drivers. Journal of International Development, forthcoming.
[22] Herzer, D., & Vollmer, S. (2012). Inequality and growth: Evidence from panel cointegration. Journal of Economic Inequality, 10(4), 489-503.
[23] Jiménez, é. M. (2006). Relaciones entre democracia y desarrollo en los países andinos. Una reflexión desde la economía política. Revista de economía institucional, 14, 167-189.
[24] Kuznets, S. (1955). Economic growth and income inequality. American Economic Review, 45, 1-28.
[25] Levine, R., & Renelt, D. (1992). A sensitivity analysis of cross-country growth regressions. American Economic Review, 82(4), 942-963.
[26] Li, H., & Zou, H. (1998). Income inequality is not harmful for growth: Theory and evidence. Review of Development Economics, 2, 318-34.
[27] Lin, S.-C., Huang, H.-C., & Weng, H.-W. (2006). A semiparametric partially linear investigation of the Kuznets' hypothesis. Journal of Comparative Economics, 34(3), 634-647.
[28] Lin, S.-C., Huang, H-C, Kimz, D.H., & Chih-ChuanYeh, C.-C. (2009). Nonlinearity between inequality and growth. Studies in Nonlinear Dynamics & Econometrics, 13(2), 1-18.
[29] Malinen, T. (2012). Estimating the long-run relationship between income inequality and economic development. Empirical Economics, 42, 209-233.
[30] Malinen, T. (2013). Inequality and growth: Another look with a new measure and method. Journal of International Development, 25(1), 122-138.
[31] Martínez, C. (2013). El efecto de la desigualdad y el acceso al crédito sobre la acumulación de capital humano. Ensayos sobre Economía Política, 31(72), 18-34.
[32] Partridge, M. (1997). Is inequality harmful for growth? Comment. American Economic Review, 87(5), 1019-1032.
[33] Partridge, M. (2005). Does income distribution affect U.S. State economic growth?, Journal of Regional Science, 45(2), 363-394.
[34] Persson, T., & Tabellini, G. (1994). Is inequality harmful for growth?. American Economic Review, 84(3), 600-621.
[35] Pesaran, M., & Smith, R. (1995). Estimating long-run relationships from dynamic heterogeneous panels. Journal of Econometrics, 68, 79-113.
[36] SEDLAC. http://sedlac.econo.unlp.edu.ar/eng/
[37] Shin, I. (2012). Income inequality and economic growth. Economic Modelling, 29(5), 2049-2057
[38] Stewart, R., & Moslares, C. (2012). Income inequality and economic growth: The case of Indian states 1980-2009-10. Cuadernos de Economía, 31(57), 41-64.
[39] Stiglitz, J. (1969). Distribution of income and wealth among individuals. Econometrica, 37(3), 382-397.
[40] Tiwari, A., Shahbaz, M., & Islam, F. (2013). Does financial development increase rural-urban income inequality?: Cointegration analysis in the case of Indian economy. International Journal of Social Economics, 40(2), 151-168.
[41] Voitchosky, S. (2005). Does the profile of income inequality matter for economic growth? Distinguishing between the effects of inequality in different parts of the income distribution. Journal of Economic Growth, 10(3), 273-96.
[42] Woo, J. (2011). Growth, income distribution, and fiscal policy volatility. Journal of Development Economics, 96(2), 289-313.