ESTABILIDAD Y
ANÁLISIS DE SEGUNDO ORDEN DE ESTRUCTURAS DE VIGAS Y COLUMNAS DE TIMOSHENKO CON
CONEXIONES SEMIRRÍGIDAS: MÉTODO PENDIENTE-DEFLEXIÓN
STABILITY AND
SECOND-ORDER ANALYSIS OF TIMOSHENKO BEAM-COLUMN STRUCTURES WITH SEMIRIGID
CONECTIONS: SLOPE-DEFLECTION METHOD
J. DARIO
ARISTIZABAL-OCHOA
Profesor, Facultad de Minas, Universidad Nacional
de Colombia, Medellín, jdaristi2@yahoo.com
Recibido para revisar julio 29 de 2008, aceptado marzo 3 de 2009, versión final marzo
10 de 2009
RESUMÉN: Un nuevo conjunto de ecuaciones pendiente-deflexión
para la viga-columna de Timoshenko de sección transversal simétrica con
conexiones semirrígidas que incluyen los efectos combinados de deformaciones
por cortante y por flexión, y los efectos de segundo orden causados por cargas
axiales es desarrollado de una manera clásica. El método propuesto que también
incluye los efectos de la componente de cortante de las fuerzas axiales
aplicadas (modelo de Haringx) tiene las siguientes ventajas: 1) puede ser
utilizado en la estabilidad y en el análisis de segundo orden de estructuras
aporticadas compuestas de vigas y columnas de Timoshenko con conexiones
rígidas, semirrígidas y simples; 2) los efectos de las conexiones están condensados
dentro de las ecuaciones pendiente-deflexión para cargas axiales de tracción y compresión
sin introducir grados de libertad ni ecuaciones adicionales; 3) es más exacto
que cualquier otro método disponible en la literatura técnica y con la
capacidad de capturar el fenómeno del pandeo de columnas bajo fuerzas de
tracción axial; 4) es poderoso, práctico, versátil y fácil de enseñar. Estudios
analíticos indican que las deformaciones por cortante incrementan las
deflexiones laterales y reducen la cargas críticas axiales de estructuras
aporticadas hechas de columnas y vigas con baja rigidez a cortante.
PALABRAS CLAVE: Viga; viga-columna; grandes deflexiones;
análisis no lineal; conexiones semirrígidas; análisis de segundo orden; estabilidad;
análisis estructural, post pandeo.
ABSTRACT: A new set of slope-deflection
equations for Timoshenko beam-columns of symmetrical cross section with
semi-rigid connections that include the combined effects of shear and bending
deformations, and second-order axial load effects is developed in a classical
manner. The proposed method that also includes the effects the shear component
of the applied axial forces (Haringx Model) has the following advantages: 1) it
can be utilized in the stability and second-order analysis of framed structures
made up of Timoshenko beam-columns with rigid, semi-rigid, and simple end
connections; 2) the effects of semi-rigid connections are condensed into the
slope-deflection equations for tension or compression axial loads without
introducing additional degrees of freedom and equations; 3) it is more accurate
than any other method available and capable of capturing the phenomena of
buckling under axial tension forces; and 3) it is powerful, practical,
versatile and easy to teach. Analytical studies indicate that shear
deformations increase the lateral deflections and reduce the critical axial
loads of framed structures made of members with low shear stiffness.
KEY WORDS: Beams; beam-columns; large
deflections; nonlinear analysis; semirigid connections; Second-order analysis;
stability; structural analysis.
1. INTRODUCCIÓN
El método pendiente-deflexión (PD) representa el punto de
inicio en la evolución del método matricial de rigidez como este es conocido actualmente
[1]. Este fue presentado en 1915 por Wilson y Maney [2] en un Bulletin desde la Universidad de
Illinois en Urbana-Champaign como un método general para ser usado en el
análisis de vigas con nudos rígidos sujetos a cargas transversales.
El método PD puede ser utilizado para
analizar todo tipo de vigas y pórticos estáticamente indeterminados. Las
ecuaciones clásicas de pendiente-deflexión son derivadas por medio del teorema
del momento-área considerando la deformación causada sólo por los momentos de flexión y despreciando los
debidos por fuerzas de cortantes y axiales. Básicamente, un número de
ecuaciones simultáneas son planteadas con incógnitas como las rotaciones
angulares y los desplazamientos de cada nodo. Una vez que estas ecuaciones han
sido solucionadas, los momentos en todos los nudos pueden ser determinados. El método
PD es simple de explicar y aplicar ya que se basa en el equilibrio de los nudos
y de los elementos. El método PD clásico es enseñado en cursos elementales de
análisis estructural [3, 4] y empleados en el diseño estructural [5] porque
este provee una perspectiva clara y completa de cómo los momentos internos y
las deformaciones están interrelacionados, conceptos que son esenciales en la
ingeniería estructural.
Sin embargo, los avances en
materiales compuestos de alta capacidad de resiliencia y baja rigidez a
cortante así como la necesidad para vigas y columnas más ligeras y resistentes
ha creado gran interés en los efectos en la cortante y análisis de segundo
orden de estructuras aporticadas. Por ejemplo, los aislantes elastoméricos y
los elementos livianos hechos de materiales poliméricos pueden someterse a grandes deflexiones
bajo combinaciones de cargas axiales y transversales sin exceder su límite elástico. Las
ecuaciones pendiente-deflexión para una viga de Timoshenko sin carga axial
incluyendo los efectos de la deformación por cortante y las cargas transversales fueron inicialmente desarrolladas
por Bryan y Baile [6].
Previamente, Lin, Glauser y
Johnson [7] habían desarrollado las ecuaciones de pendiente-deflexión para
elementos de alma abierta incluyendo el efecto de la deformación de cortante,
carga axial y extremos con placas rígidas. Por otro lado, la estabilidad y el
análisis de segundo orden de columnas esbeltas y de estructuras con conexiones semirrígidas
fueron investigados por Aristizabal-Ochoa [8] y [9] empleando las funciones
clásicas de estabilidad. Sin embargo, la estabilidad de estructuras aporticadas
usando el método clásico de pendiente-deflexión incluyendo los efectos
combinados de las deformaciones por cortante y flexión, los efectos de segundo
orden P-D, y conexiones semirrígidas no es todavía conocido.
El principal objetivo de esta
publicación es presentar un nuevo conjunto de ecuaciones de pendiente-deflexión
para la estabilidad y el análisis de segundo orden de estructuras aporticadas
hechas de vigas y columnas de Timoshenko de sección transversal simétrica con
conexiones semirrígidas bajo cargas axiales en los extremos incluyendo los efectos
combinados de: 1) deformaciones de flexión y de cortante; y 2) la componente inducida
por las cargas axiales en la cortante (Modelo de Haringx).
El método propuesto el cual es
basado en las funciones de estabilidad "modificadas" para la viga-columna de
Timoshenko con conexiones semirrígidas desarrolladas por Aristizabal-Ochoa [10]
y [11] posee las siguientes ventajas: 1) los efectos de las conexiones son
condensadas dentro de las ecuaciones de pendiente-deflexión para cargas axiales
de tracción o de compresión sin introducir grados de libertad y ecuaciones
adicionales; 2) es más exacto que cualquier otro método disponible y capaz de
capturar el fenómeno de pandeo bajo cargas axiales de tracción en columnas
cortas de elastoméricos laminados comúnmente usados como aislantes sísmicos en
edificios; 3) el método es poderoso, práctico, versátil y fácil de enseñar.
Cuatro ejemplos son incluidos que demuestran la eficacia del método propuesto y
sus ecuaciones.
2. MODELO
ESTRUCTURAL
2.1 Suposiciones
Consideremos una viga-columna prismática que conecta
los puntos A y B como muestra la fig. 1(a). El elemento esta formado por una
viga-columna A'B', y las conexiones AA' y BB' a flexión con rigideces ka ykb en los extremos A y B, respectivamente. Se supone que la
viga-columna A'B' de luz L: 1) se flecta
alrededor del los ejes principales de su sección transversal con un momento de
inercia I, área efectiva de cortante As; 2) está hecha de un
material elástico lineal homogéneo con modulo de Young y modulo de cortante E y G,
respectivamente; 3) su eje centroidal es una línea recta; y 4) esta cargada axialmente
en el extremo A con P a lo largo de
su eje centroidal.
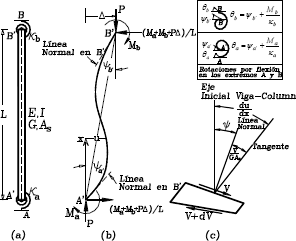
Figura 1. Viga-Columna bajo momentos en los extremos con
conexiones semirígidas: (a) modelo estructural; (b) grados de libertad, fuerzas
y momentos en el planos de la flexión; (c) rotaciones en una sección
transversal y en los extremos A y B
Figure 1. Beam-Column under end moments with
semi-rigid connections: (a)
Structural Model; (b) Degrees of Freedom, Forces and Moments in the plane of
bending; (c) Rotations at a cross section and at ends A and B
Los conexiones a flexión tienen
rigideces ka y kb (cuyas unidades son en
fuerza-distancia/radian) en el plano principal del elemento. Las relaciones Ra=ka/(EI/L) y Rb=kb/(EI/L) se denominan como
los índices de rigidez de las conexiones. Estos índices varían desde
cero (i.e., Ra= Rb= 0) para conexiones
simples (o articuladas) hasta infinito (Ra= Rb= ∞) para conexiones
restringidas o rígidas. Nótese que el algoritmo propuesto puede ser empleado en
el análisis inelástico de viga-columnas con comportamiento inelástico
concentrado en las conexiones. Esto puede llevarse a cabo mediante la
actualización de la rigideces ka y kb para cada incremento
de carga en un incremento lineal adoptado.
Por conveniencia los siguientes
dos parámetros son introducidos:
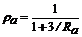 ; y
; y 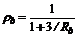 (1a-b)
(1a-b)
Donde ra y rb son llamados los factores de
fijeza. Para conexiones articuladas, los factores de fijeza r y los índices de rigidez R son cero; pero para conexiones rígidas, el factor de fijeza es 1
y el índice de rigidez es infinito. Por lo tanto el factor de fijeza solo puede
variar desde 0 hasta 1 para conexiones elásticas (mientras el índice de rigidez R puede variar desde 0 hasta ∞), es más conveniente
usar en los análisis elásticos de estructuras con conexiones semirrígidas.
3. PROPUESTA DE LAS ECUACIONES DE
PENDIENTE-DEFLEXIÓN
Para investigar la estabilidad lateral y análisis
de segundo-orden de estructuras aporticadas con conexiones semirrígidas, es
necesario primero establecer las relaciones entre los momentos flectores en los
extremos y las correspondientes rotaciones para cada miembro del pórtico y
luego aplicar las condiciones de compatibilidad de deformaciones en cada nudo.
La aplicación del método clásico de pendiente-deflexión en la estabilidad de
pórticos planos (con conexiones rígidas y sin cargas transversales excluyendo
los efectos por cortante) es bien explicado por Salmon y Johnson [5], páginas
835-843. Las ecuaciones propuestas de pendiente-deflexión para pórticos planos
con conexiones semirrígidas incluyendo los efectos por cortante y sin carga
transversal a lo largo de cada miembro son como siguen:
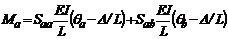 (2a)
(2a)
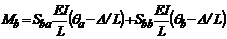 (2b)
(2b)
Donde los valores de 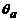 y
y 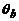 son las rotaciones de los extremos A
y B medidos con respecto la eje inicial del miembro, y D/L el ángulo de rotación de la cuerda del miembro AB. Ambas
rotaciones y momentos en los extremos (Ma y Mb) son positivas en
sentido de las agujas del reloj como se muestra en la fig. 1. Saa, Sab, Sba y Sbb son llamados
coeficientes de rigidez de la viga-columna de Timoshenko AB con conexiones semirrígidas
en ambos extremos. Los coeficientes son listados en la sección que sigue para su
fácil referencia.
son las rotaciones de los extremos A
y B medidos con respecto la eje inicial del miembro, y D/L el ángulo de rotación de la cuerda del miembro AB. Ambas
rotaciones y momentos en los extremos (Ma y Mb) son positivas en
sentido de las agujas del reloj como se muestra en la fig. 1. Saa, Sab, Sba y Sbb son llamados
coeficientes de rigidez de la viga-columna de Timoshenko AB con conexiones semirrígidas
en ambos extremos. Los coeficientes son listados en la sección que sigue para su
fácil referencia.
3.1 Coeficientes de rígidez de primer orden
3.1.1 Para P=0
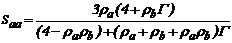 (3)
(3)
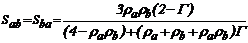 (4)
(4)
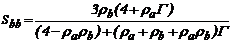 (5)
(5)
3.2 Coeficientes de rígidez de segundo orden
3.2.1 Para 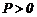 (compresión) o
(compresión) o
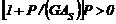
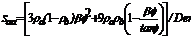 (6)
(6)
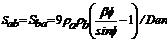 (7)
(7)
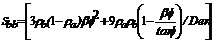 (8)
(8)
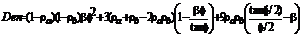
3.2.1 Para P< 0 (tensión) y 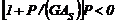
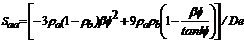 (9)
(9)
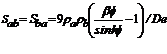 (10)
(10)
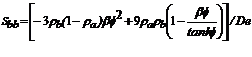 (11)
(11)
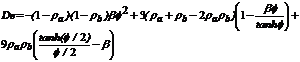 Donde:
Donde:  ; y
; y  .
.
Nótese que
el método propuesto y las ecuaciones listadas arriba son válidos para miembros
sujetos a fuerzas axiales de tracción y compresión. Cuando 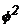 es negativo (i.e.,
es negativo (i.e., 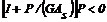 ), los siguientes tres cambios fueron realizados en las ecs. (6)-(8) para
obtener las ecs. (9)-(11): 1) senf por i senhf; 2) tanf por i tanhf; y 3) f por if (donde: i=
), los siguientes tres cambios fueron realizados en las ecs. (6)-(8) para
obtener las ecs. (9)-(11): 1) senf por i senhf; 2) tanf por i tanhf; y 3) f por if (donde: i= 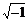 ). Las ecuaciones (2a) y (2b) son derivadas en el Apéndice I.
). Las ecuaciones (2a) y (2b) son derivadas en el Apéndice I.
Para verificar los coeficientes
dados por las ecs. (3)-(5), los numeradores y denominadores de las ecs. (6)-(8)
deben ser diferenciados cuatro veces de acuerdo con la regla de L'Hospital y
luego aplicar el límite P= 0. Sin
embargo, realizar este proceso es realmente tedioso y engorroso, las
derivaciones de las ecs. (3)-(5) son también presentadas en el Apéndice I.
Los cuatro ejemplos presentados
en la sección que sigue muestran la efectividad, simplicidad y precisión del
método pendiente-deflexión propuesto y las correspondientes ecuaciones listadas
arriba. Los ejemplos 1 y 2 son acerca del análisis de estabilidad de
estructuras viga-columna sujetas a fuerzas en los nudos causando tensión y/o
compresión en los miembros. Los ejemplos 3 y 4 muestran la aplicación del
método propuesto en pórticos planos sujetos a cargas axiales de compresión y/o
de tracción.
4. EJEMPLOS
4.1 Ejemplo 1- Análisis de
Segundo orden de una columna en voladizo bajo varias cargas
Determine la ecuación carga-deflexión de
segundo-orden de la columna en voladizo de la fig. 2. Compare las expresiones
resultantes con aquellas obtenidas por Timoshenko y Gere [12], paginas 5 y 13
para una columna en voladizo Bernoulli-Euler empotrada (esto es, r= b= 1).
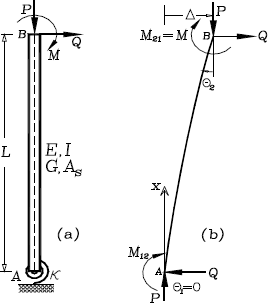
Figura 2. EJEMPLO 1:
Análisis de segundo orden de una columna en voladizo: (a) Modelo estructural; y
(b) Forma deflectada y acciones en los extremos
Figure 2. EXAMPLE 1: Second-Order Analysis of
a Cantilever Column: (a) Structural Model; and (b) Deflected Shape and end
Actions
Solución: Aplicando equilibrio
(fig. 2b):
M21= M (12)
M12+ M+ PD+ QL= 0 (13)
Ahora utilizando las ecs. (2a) y
(2b)
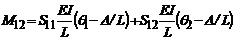 (14)
(14)
 (15)
(15)
En este ejemplo ra= r y rb=
1; luego para 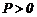 (compresión) y usando las ecs. (6)-(8):
(compresión) y usando las ecs. (6)-(8):
 (16)
(16)
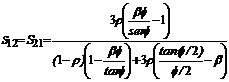 (17)
(17)
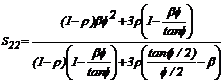 (18)
(18)
Sabiendo que 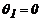 y utilizando las ecs. (14) y (15)
las siguientes expresiones pueden ser obtenidas de las ecs. (12) y (13):
y utilizando las ecs. (14) y (15)
las siguientes expresiones pueden ser obtenidas de las ecs. (12) y (13):
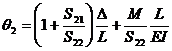 (19)
(19)
y 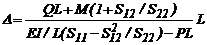 (20)
(20)
La ecuación (20) puede ser
reducida a 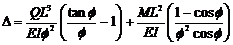 la cual es
la cual es
idéntica a la superposición de las ecs. (g) y
(1-33) presentadas por Timoshenko y Gere [12], páginas 5 y 14 para casos
particulares de una columna en voladizo Bernoulli-Euler empotrada (r=b= 1) sometida a carga
lateral Q y momento M, respectivamente. El comportamiento al
post-pandeo y a grandes deflexiones de una columna Timoshenko en voladizo
sujeta a cargas en el extremo superior es discutido en detalle por Aristizábal-Ochoa
[11].
4.2 Ejemplo 2-. Estabilidad de una columna de dos luces con soporte intermedio
Determine la carga crítica de pandeo de una columna
continua de dos luces mostrada en la fig. 3a. Suponga que los miembros 1 y 2
son horizontales inicialmente con propiedades (GAs)1, (EI)1,
l1 y (GAs)2, (EI)2, l2,
respectivamente. También suponga que las cargas aplicadas aP y P permanecen horizontales y son aplicadas en los nudos 2 y 3, respectivamente. Incluya los efectos
de la rigidez transversal S del soporte intermedio 2. Compare los
resultados obtenidos con los presentados por Timoshenko y Gere [12], páginas 70
y 99 cuando el miembro es hecho de dos viga-columnas Euler-Bernoulli.
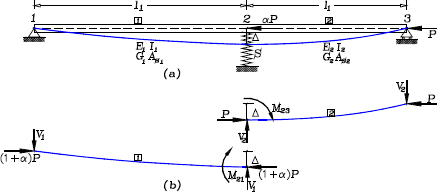
Figura 3. Ejemplo 2: Análisis
de estabilidad de una viga-columna de dos luces con un soporte elástico
intermedio: (a) Modelo estructural y forma deflectada; y (b) Fuerzas en cada
elemento
Figure 3. Example
2: Stability Analysis of a two Span Beam-column with an Intermediate Elastic
Support: (a) Structural Model and Deflected Shape; and (b) Forces and Moments
on Elements 1 and 2
Solución: Del equilibrio de
momento de los segmentos de viga 1 y 2 (fig. 3b) se obtiene las siguientes dos
ecuaciones:
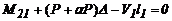 (21)
(21)
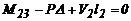 (22)
(22)
Del momento de equilibrio del
nudo 2:
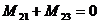 (23)
(23)
Sabiendo que V1 +V2= SD y utilizando la ec. (23), entonces de las ecs. (21) y (22) se
obtiene la siguiente expresión:
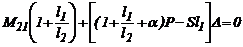 (24)
(24)
En este ejemplo ra= 0 y rb= 1 para el elemento 1, y ra= 1 y rb= 0 para el elemento 2. Luego
llamando 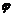 la rotación a flexión del nodo 2 con
respecto al eje horizontal y utilizando las ecs. (2):
la rotación a flexión del nodo 2 con
respecto al eje horizontal y utilizando las ecs. (2):
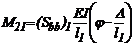 y
y 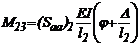
Donde para 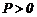 y
y 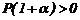 y utilizando las ecs. (6)-(8):
y utilizando las ecs. (6)-(8):
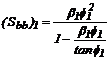 y
y 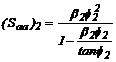
Ahora, las Ecs. (23)-(24) pueden
ser presentadas en forma matricial como sigue:
 (25)
(25)
Haciendo el determinante de la
matriz de 2'2 en la ec. (25) la
ecuación característica puede ser determinada y las cargas de pandeo pueden ser
calculadas. Por ejemplo para el caso particular de EI1= EI2 y l1= l2= L/2 y S= 0, la ecuación característica es
reducida a:
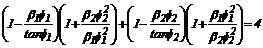 (26)
(26)
La ecuación (26) produce
resultados idénticos a los obtenidos por Timoshenko y Gere [1961, p. 99 ec.
(2-42)] cuando el miembro es simplemente apoyado hecho de una columna
Euler-Bernoulli (i.e., b1= b2= 1) con cargas de compresión en la mitad de la luz (nodo
2) y en extremo del nodo 3.
Otro caso interesante es cuando
el valor de S se vuelve muy grande
haciendo D» 0, y entonces la ecuación
característica es reducida al primer término de la ec. (25) como sigue:
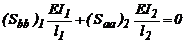
ó 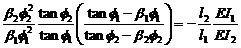 (27)
(27)
La ecuación (27) produce
resultados idénticos a los obtenidos por Timoshenko y Gere [1961, p. 67, ec.
(b)] para una columna Euler-Bernoulli de dos luces (esto es con b1=b2=1) con cargas de compresión
localizadas en los nodos 1 y 3.
La figura 4 muestra una serie de
diagramas de interacción de P/(EI/L2)-versus-aP/(EI/L2) para
diferentes valores de S/(EI/L3)
obtenidos utilizando la ec. (25) para el caso particular de l1= l2= L/2, (GAs)1=(GAs)2=∞ y (EI)1= (EI)2= EI. La
fig. 5 muestra las variaciones de la carga crítica de pandeo de una columna
simplemente apoyada con la rigidez S del apoyo elástico intermedio localizado en la mitad de la luz para diferentes
valores de GAs/(EI/L2).
Nótese que: 1) los valores
indicados en la fig. 4 a
la curva S= 0 son idénticos a los
presentados por Timoshenko y Gere [12], página 100 tabla 2-6 para n= 1; 2) la capacidad de carga de pandeo
de la viga-columna es afectada significativamente no solo por la ubicación y
rigidez del apoyo intermedio sino también por la magnitud de la rigidez a
cortante de cada segmento como es mostrado por las curvas de la fig. 5; y 3) la
curva correspondiente a GAs/(EI/L2)=
∞ en la fig. 5 muestra que la carga crítica aumenta en aproximadamente en
la misma proporción que S Esta curva
es idéntica a la presentada por Timoshenko y Gere [12], página 73.
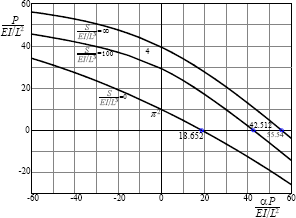
Figura 4. Diagramas de interacción P/(EI/L2)-vs-aP/(EI/L2) para la viga-columna de
dos luces del Ejemplo 2 [para el caso particular de l1= l2= L/2, (GAs)1= (GAs)2= ∞ y (EI)1= (EI)2= EI] con un soporte elástico intermedio S/(EI/L3)= ∞, 100, y 0
Figure 4. Interaction
Diagrams P/(EI/L2)- vs.- aP/(EI/L2) for the two-span
beam-column of Example 2 [for the
particular case of l1 = l2= L/2, (GAs)1=(GAs)2= ∞ and (EI)1= (EI)2= EI] with an Intermediate Elastic
Support with Sc/(EI/L3)= ∞, 100, and 0
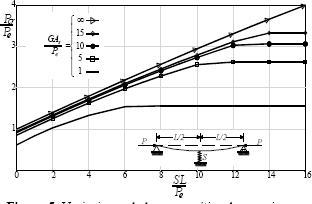
Figura 5. Variaciones
de la carga crítica de una viga-columna simplemente soportada con la rigidez S del soporte elástico intermedio (donde Pe= p2EI/L2)
Figure 5. Variations of the critical Load of a simply supported beam-column with
the stiffness of the intermediate elastic support S (where Pe= p2EI/L2)
4.3
Ejemplo 3-. Análisis de estabilidad de un
pórtico con conexiones semirrígidas
Determine la carga crítica de pandeo de un pórtico
doblemente simétrico con conexiones semirígidas viga-a-columna de la fig. 6.
Los miembros horizontales están conectados a las columnas verticales en ambos
extremos con conexiones semirígidas de rigidez k (o factor de fijeza ρ). Suponga que los miembros verticales y horizontales son
rectos con las siguientes propiedades (G,
E, A, As, I, h) y (G1,
E1, A1, As1, I1, b),
respectivamente. También suponga que para el
primer modo de pandeo como es mostrado en la Fig. 4 las cargas aplicadas P y Q son siempre verticales y horizontales, respectivamente. Incluya los
efectos de las conexiones. Compare los resultados con los presentados por
Timoshenko y Gere (1961, p. 62) cuando las conexiones viga-a-columna son
rígidas (ρ= 1). Estudie la
estabilidad del pórtico bajo fuerzas de tracción y de compresión.
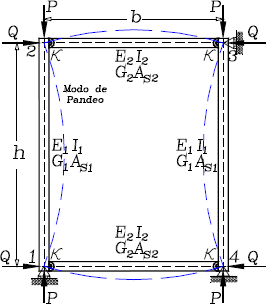
Figura 6. Ejemplo 3: Análisis de estabilidad de un
pórtico doblemente simétrico con conexiones semirrígidas viga-a-columna (veáse Timoshenko
& Gere [12], página 34)
Figure 6. Example 3: stability analysis of a
double symmetrical frame with semirigid connections
Solución: En este pórtico
particular ra=rb=1 para ambas columnas, y ra=rb=r para ambas vigas. Ahora, del equilibrio de momento del nodo 1:
(After Timoshenko & Gere [12], p. 34)
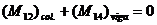 (28)
(28)
Debido a la simetría en el modo
de pandeo, (i.e., 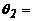
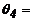 -
- 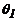 y consecuentemente una sola rotación desconocida y sin deriva entre los
extremos de los miembros), entonces empleando las ecs. (2a) y (2b):
y consecuentemente una sola rotación desconocida y sin deriva entre los
extremos de los miembros), entonces empleando las ecs. (2a) y (2b):
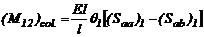 (29)
(29)
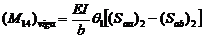 (30)
(30)
Donde:
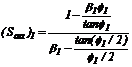 ;
; 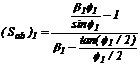 ;
;
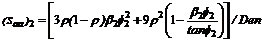 ;
;
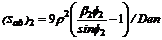 ; y
; y
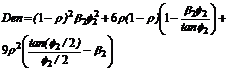
Sustituyendo estas últimas cuatro
expresiones, en las ecs. (29) y (30) y luego en la ec. (28), se obtiene la
siguiente ecuación característica:
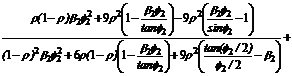
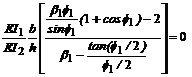 (31)
(31)
La ecuación (31) puede ser reducida a
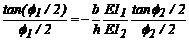
para un pórtico con columnas y vigas
Bernoulli-Euler con r= 1 la cual es idéntica a
la ec. (2-25) de Timoshenko y Gere [12],
página 63.
Las figs. 7a-c muestran una serie
de diagramas de interacción P/(EI/L2)-versus-Q/(EI/L2) para diferentes valores
de r y GAs/(EI/L2) todos
obtenidos de la ec. (31) para el caso particular de h= b= L, (GAs)1= (GAs)2=GAs y (EI)1=(EI)2=EI.
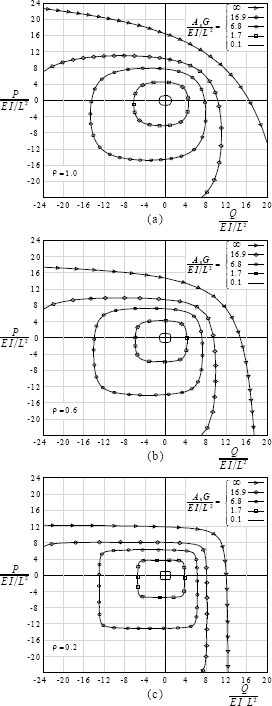
Figura 7. Diagramas
de interacción P/(EI/L2)-vs-Q/(EI/L2) para un pórtico
doblemente simétrico del ejemplo 3 con factor de fijeza viga-a-columna: (a) r= 1; (b) r= 0.6; y (c) r= 0.2
Figure 7. Interaction diagrams P/(EI/L2)-vs-Q/(EI/L2) for a double symmetrical frame
of Example 3 with semirigid connections with : (a) r= 1; (b) r= 0.6; and (c) r=0.2
Nótese que: 1) las capacidades de
carga de pandeo son afectadas significativamente no solamente por la rigidez de
las conexiones viga-a-columna sino también por la magnitudes de la rigidez a
cortante de los miembros; y 2) el pandeo bajo fuerzas axiales de tracción es
una imagen simétrica respecto al eje horizontal del pandeo bajo fuerzas axiales
de compresión para miembros cortos con baja rigidez a cortante como los
soportes elastoméricos de múltiples capas así como lo reporta Kelly [13].
Ejemplo 4-. Análisis de estabilidad de un pórtico plano asimétrico
Determine las cargas de pandeo de un pórtico plano
con deriva lateral parcialmente inhibida mostrado en la fig. 8a. Los factores
de fijeza ρ de la viga-a-columna y
las conexiones semirígidas de la columna-a-fundación son indicadas en la fig.
7a. Suponga que: 1) los miembros horizontales y verticales son rectos
inicialmente con las siguientes propiedades [(EI)1, (GAs)1, h1], [(EI)2, (GAs)2,
h2] y [(EI)3, (GAs)3,,
L], respectivamente; 2) el modo de pandeo es como lo muestra la Fig. 8a y que las cargas
aplicadas P y aP son siempre verticales.
Incluya los efectos de la rigidez S del arrostramiento lateral en el nodo 2. Compare los resultados con los
presentados por Salmon Johnson [5] para un pórtico simétrico hecho de miembros
Euler-Bernoulli cuando las conexiones viga-a-columna son rígidas (ρ1=ρ2=1) y las bases de las
columnas son perfectamente articuladas (ρ3= ρ4= 0) y a= 1. Discuta también la estabilidad del pórtico bajo
fuerzas de tracción.
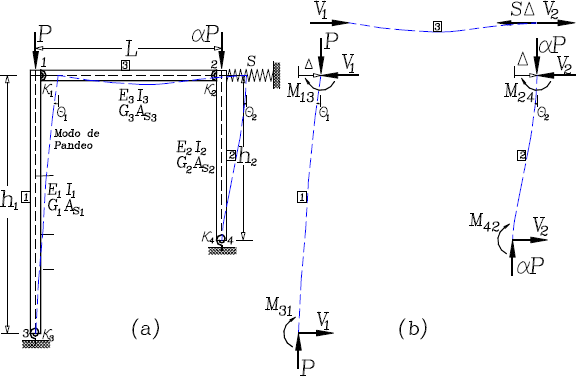
Figura 8. Ejemplo 4: Análisis
de estabilidad de un pórtico asimétrico con deriva lateral parcialmente
inhibida: (a) Modelo estructural y cargas; (b) Fuerzas y momentos en cada
miembro deflectado.
Figure 8. Example 4: Stability Analysis of an
Unsymmetrical Frame with Lateral Sway Partially Inhibited: (a) Structural Model and Loads;
(b) Forces on each Deflected Member
Solución: Las variables
desconocidas del pórtico 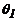 ,
, 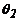 y D se muestras en la fig. 7a. Ahora,
del equilibrio de momento de los nodos 1 y 2:
y D se muestras en la fig. 7a. Ahora,
del equilibrio de momento de los nodos 1 y 2:
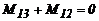 (32)
(32)
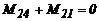 (33)
(33)
La tercera ecuación es obtenida
aplicando equilibrio a cada miembro (ver fig. 8b):
Columna 1: M31 + M13 + PD - V1h1= 0
Columna 2: M42+ M24 + aPD - V1h1= 0
Viga: V1 + V2 -SD= 0
De estas tres condiciones de
equilibrio y las ecs. (32) y (33), se obtiene entonces la ec. (34):
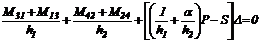 (34)
(34)
Ahora usando las ecs. (2a) y
(2b):
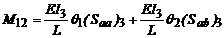 (35)
(35) 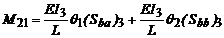 (36)
(36) 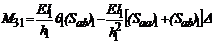 (37)
(37)
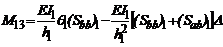 (38)
(38)
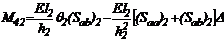 (39)
(39)
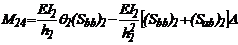 (40)
(40)
Sustituyendo (35)-(40) en las Ecs. (32), (33) y
(34) se obtiene el siguiente sistema homogéneo 3'3:
 (41)
(41)
Donde: 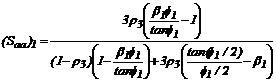 ;
; 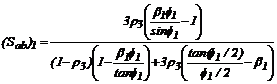 ;
; 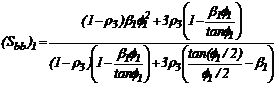 ;
; 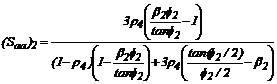 ;
; 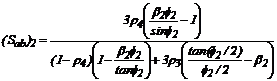 ;
;  ;
; 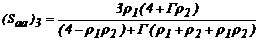 ;
; 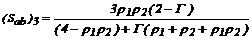 ;
; 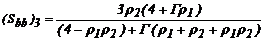 .
.
Haciendo el determinante de la
matriz de 3'3 de la ec. (41) igual a
cero, la ecuación característica es determinada y así las cargas de pandeo
pueden ser calculadas.
Para el caso particular de un
pórtico simétrico no arriostrado con columnas y vigas Bernoulli-Euler con EI1= EI2, b1= b2 = b3 = 1, h1= h2= h, a= 1, r1= r 2 =1, r3= r 4 =0, S=G = 0, y suponiendo que q1= q 2 la ec. (41) característica puede
ser reducida a:
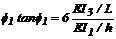 (42)
(42)
Otro caso interesante es cuando
el valor de S se hace muy grande
haciendo D» 0 (esto es, para un
pórtico con deriva inhibida), entonces la ecuación característica es reducida a
las primeras dos filas y columnas de la ec. (41):
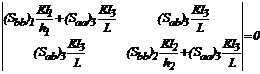 (43)
(43)
Para el caso particular de un
pórtico simétrico con columnas y vigas Bernoulli-Euler con EI1= EI2, b1= b2= b3= 1, h1= h2= h, a= 1, r1= r 2 =1, r3= r 4= 0, G= 0 y asumiendo que q1= -q 2 la ec. (43) característica puede
ser reducida además a:
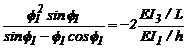 (44)
(44)
Las Ecs. (42) y (43) son
idénticas a las Ecs. (14-2-30) y (14-2-18) presentadas por Salmon y Gere [5]
páginas 900-912 para pórticos simétricos arriostrados y no arriostrados,
respectivamente. Se debe enfatizar que la
ec. (42) es
únicamente capaz de capturar los modos antisimétricos de pandeo del pórtico
simétrico no arriostrado (ya que se supuso que q1= q 2). Así mismo, la ec. (44) es únicamente capaz de capturar los modos
simétricos de pandeo de este pórtico simétrico arriostrado (ya que se supuso
que q1= -q 2). La fig. 9 muestra que los tres primeros auto-valores se obtuvieron
empleando la ecuación característica (43) y los dos primeros obtenidos usando
la ec. (44). Por tanto, el método propuesto es
más poderoso desde que es capaz de capturar todos los modos de pandeo
incluyendo aquellos bajo fuerzas axiales de tensión (como se mostró en los
ejemplos 2 y 3).
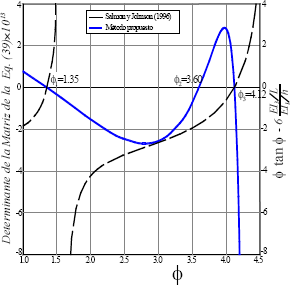
Figura 9. Comparación
de resultados para un pórtico simétrico con deriva lateral inhibida usando el
método propuesto y la formula simplificada de Salmon y Johnson [5]
Figure 9. Comparison of Results for a Symmetrical Frame with Lateral Sway Inhibited using
the proposed method and a simplified formula after Salmon and Johnson [5]
5. RESUMEN Y CONCLUSIONES
Un nuevo conjunto de ecuaciones
pendiente-deflexión que incluyen los efectos de las deformaciones por cortante
y la componente a cortante inducida por las fuerzas axiales aplicadas (Modelo
de Haringx ) son derivadas y luego empleadas en la estabilidad y análisis de
segundo-orden de estructuras aporticadas hechas de vigas y columnas de
Timoshenko con conexiones rígidas, semirrígidas y simples. El método propuesto
está basado en las funciones de estabilidad "modificadas" para viga-columnas
con conexiones semirrígidas desarrolladas por Aristizábal-Ochoa [10] y [11]. La
validez y efectividad de las ecuaciones propuestas son verificadas contra
cuatro soluciones bien documentadas sobre la estabilidad elástica y análisis de
segundo-orden de viga-columnas y pórticos planos.
Las ventajas del método propuesto
son: 1) los efectos de las conexiones semirrígidas son condensadas dentro de
dos ecuaciones no lineales con tres incógnitas (las rotaciones en los extremos
y la deriva lateral entre los extremos de los miembros) para cargas axiales de
tracción y de compresión sin introducir
grados de libertad y ecuaciones adicionales; 2) más preciso que cualquier otro
método disponible y capaz de capturar el fenómeno de pandeo bajo fuerzas
axiales de tracción. Estas ventajas son particularmente importantes en el
análisis de columnas cortas como son los apoyos elastoméricos laminados
comúnmente usados en aislamiento sísmico de edificios; y 3) el método es
poderoso, práctico, versátil, y fácil de enseñar.
Estudios analíticos indican que
los efectos de la cortante aumentan las deflexiones laterales de estructuras
aporticadas, y reducen sus cargas críticas axiales. Los efectos de las
deformaciones por cortante y efectos P-D (de segundo-orden) deben ser
considerados en el análisis columnas con áreas de cortante relativamente bajas
(como vigas y columnas de alma abierta o perforada) o bajo módulo de cortante G (como soportes elastoméricos y
columnas cortas hechas de materiales compuestos) resultando en miembros con
rigidez a cortante GAs del
mismo orden de magnitud de EI/L2. Los efectos de cortante
son también de gran importancia en la estática, estabilidad y comportamiento
dinámico de soportes elastoméricos laminados usados en el aislamiento sísmico
de edificios.
6. AGRADECIMIENTOS
Esta investigación fue llevada a cabo por la Universidad Nacional
de Colombia, Facultad de Minas en Medellín. El autor quiere expresar su aprecio
a la Escuela
de Ingeniería Civil, al DIME por el apoyo financiero y también a Jhon
Monsalve-Cano, Jaime Hernández-Urrea, Camilo Builes-Mejia y David Padilla-Llano
miembros del Grupo de Estabilidad Estructural en la preparación de los cuatro
ejemplos.
7. APÉNDICE I
7.1 Derivación de las Ecs. (2a) y (2b)
El análisis de estabilidad de una columna
prismática incluyendo las deformaciones por flexión y cortante (figs. 1a-c) es
formulada usando la aproximación "modificada" propuesta por Timoshenko y Gere
(1961, pagina 134). Esta aproximación ha sido utilizada por Kelly [13] en el
análisis de apoyos elastoméricos de aislamiento y por Aristizábal-Ochoa [10] y
[11] en el análisis de estabilidad de columnas y pórticos. Las ecuaciones
gobernantes son:
bEI u''(x) + P u(x)= -Ma - (Ma +Mb +PD) 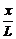 (45a)
(45a)
bEI y''(x) + Py(x)= 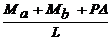 (45b)
(45b)
Donde: u(x)= deflexión lateral de la
línea central de la viga-columna; y y(x)=rotación de la sección transversal debido solamente a
flexión como muestra las figs. 1b-c.
Las soluciones de las ecuaciones
(45a)-(45b) diferenciales lineales de segundo orden son:
u(x)= A
cos( 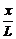 f) + Bsen(
f) + Bsen( 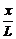 f) +
f) + 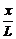
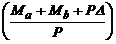 -
- 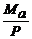 (46a)
(46a)
y(x) = C cos( 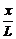 f) + D sen(
f) + D sen( 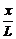 f) +
f) +
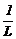
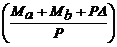 (46b)
(46b)
Los coeficientes desconocidos A, B, C, y D pueden ser obtenidos de las siguientes condiciones de borde:
En A' (x= 0): u =0, y = ya
En B' (x= h): u =D, y y = yb
Donde: ya y yb'= rotaciones de las secciones transversales en los
extremos A' y B' con respecto al eje vertical debido a la flexión,
respectivamente.
Por lo tanto:
A= 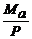 ; B=
; B= 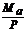 tan(f/2) -
tan(f/2) - 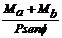 ;
;
C=ya' - 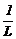
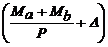 ;
;
D= 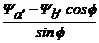 -
- 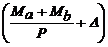 tan(f/2)
tan(f/2)
Ya que 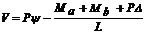 y u'=y +V/(GAs)
y u'=y +V/(GAs)
las siguientes expresiones
para ya' y yb' pueden ser obtenidas:
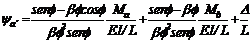 (47a)
(47a)
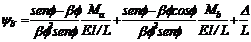 (47b)
(47b)
Sin embargo, las rotaciones en
los extremos A y B son: 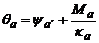 y
y  , respectivamente. Por lo tanto:
, respectivamente. Por lo tanto:
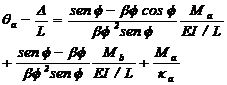 (48a)
(48a)
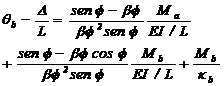 (48b)
(48b)
Donde: D= deriva relativa del
extremo B con respecto al extremo A; y qa y qb= rotaciones de los extremos A y B debido a flexión con
respecto al eje vertical, respectivamente.
Nótese que las ecs. (47a) y (47b)
son idénticas a las derivadas por Salmon y Johnson [5] página 902 para columnas
Bernoulli-Euler (cuando b=1). Ahora, expresando
ecs. (48a) y (48b) en forma matricial, y luego invirtiendo la matriz de
coeficientes y usando las expresiones (1a) y (1b) [o Ra=3ra/(1-ra) y Rb=3rb/(1-rb)], las ecs. (2a) y (2b)
pueden ser obtenidas.
7.2 Derivaciones de las ecuaciones (3)-(5)
Las ecuaciones gobernantes (45a) y (45b) cuando P= 0 son reducidas a:
bEI u''(x)= -Ma -
(Ma +Mb ) 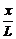 (49a)
(49a)
bEI y''(x)= 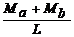 (49b)
(49b)
Las ecuaciones (47a) y (47b) son
mucho más simples de resolver. Después de aplicar las condiciones de borde
[esto es: u= 0, y = ya' en A' (x=
0); y u= D y y = yb' en B' (x= L)] sus soluciones son:
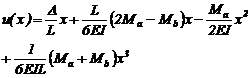 (50a)
(50a)
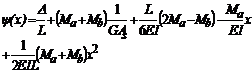 (50b)
(50b)
Sabiendo que: y= u'-V/(GAs) y 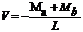 , ya
, ya
y yb pueden ser obtenidas directamente
de la ec. (50b):
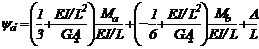 (51a)
(51a)
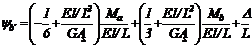 (51b)
(51b)
Como se explicó previamente, las
rotaciones en A y B son: 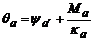 y
y 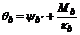 , respectivamente. Por lo tanto:
, respectivamente. Por lo tanto:
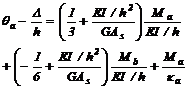 (52a)
(52a)
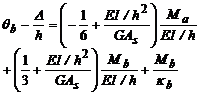 (52b)
(52b)
Expresando las ecuaciones (52a) y
(52b) en forma matricial y luego invirtiendo la matriz de coeficientes y
utilizando Ra=3ra/(1-ra) y Rb=3rb/(1-rb), las ecuaciones (2a)-(2b) y(3)-(4) pueden ser
obtenidas.
8. APÉNDICE II. REFERENCIAS
[1] SAMUELSSON, A. AND ZIENKIEWICZ, O. C. "History of the Stiffness Method," International Journal for Numerical Methods in Engineering, Wiley InterScience, Vol. 67, 149-157, 2006.
[2] WILSON, W. M. AND MANEY, G. A. "Slope-Deflection Method," University of Illinois Engineering Experiment Station, Bulletin 80, 1915.
[3] NORRIS, C. H. AND WILBUR, J. B. "Elementary Structural Analysis," McGraw-Hill Book Co., 2nd Edition, 1960.
[4] KASSIMALI, A. "Structural Analysis," Thomson-Engineering, 2nd edition, 1998.
[5] SALMON, C. G. AND JOHNSON, J.E. "Steel Structures: Design and Behavior," 4th Ed., HarperCollins College Publishers (Chapter 14), 1996.
[6] BRYANT, R. H. AND BAILE, O. C."Slope Deflection Analysis Including Transverse Shear," J. of the Structural Division, Vol. 103, (2), 443-446, 1977.
[7] LIN, F. J., GLAUSER E. C., AND JOHNSTON B. J. "Behavior of Laced and Battened Structural Members," J. Struct. Engrg., ASCE, 123(5), 1377-1401, 1960.
[8] ARISTIZÁBAL-OCHOA, J. DARÍO "First- and Second-Order Stiffness Matrices and Load Vector of Beam-Columns with Semi-rigid Connections," J. Struct. Engrg., ASCE, 123(5), 669-678, 1997.
[9] ARISTIZÁBAL-OCHOA, J. DARÍO."Story Stability of Braced, Partially Braced, and Unbraced Frames: Classical approach," J. Struct. Engrg., ASCE, 123(6), 799-807, 1977.
[10] ARISTIZÁBAL-OCHOA, J. DARÍO "Column Stability and Minimum Lateral Bracing: Effects of Shear Deformations," J. of Engineering Mechanics, Vol. 130 (10), pp. 1223-1232, 2004.
[11] ARISTIZÁBAL-OCHOA, J. DARÍO. "Large Deflection and Postbuckling Behavior of Timoshenko Beam-Columns with semirigid connections including Shear and Axial Effects," ELSEVIER Journal of Engineering Structures, Vol. 29 (6), pp. 991-1003, 2007.
[12] TIMOSHENKO, S. AND GERE, J. "Theory of Elastic Stability," 2nd Ed., McGraw-Hill, Chapter II, 1961.
[13] KELLY, J. M. "Tension Buckling in multilayer Elastomeric Bearings," J. of Engineering Mechanics, Vol. 129 (12), Nov., 2003, pp. 1363-1368. Discussion by Aristizábal-Ochoa, J. Darío, Vol. 131 (1), 106-108, 2005.
9. NOTACIÓN
Los siguientes símbolos son
usados en este documento:
As= área efectiva de
cortante de la sección transversal de la viga-columna;
E = módulo de Young del
material;
G= modulo de cortante del
material;
L= longitud de la
viga-columna AB;
I= momento principal de
inercia de la viga-columna alrededor del eje de flexión;
Ma y Mb= momentos flectores en los extremos A y B,
respectivamente;
P= carga axial aplicada en
A (+ compresión, -tracción);
Pcr= carga
crítica axial;
Pe = p2EI/L2 =carga crítica de Euler;
Ra y Rb= índices de rigidez de las conexiones a flexión en A
y B, respectivamente;
u(x)= deflexión lateral de la línea central de la viga-columna
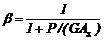 = factor de reducción del la rigidez a flexión causada por la cortante;
= factor de reducción del la rigidez a flexión causada por la cortante;
D= deriva del extremo B
con respecto a A;
ka y kb= rigidez a flexión de
las conexiones en los extremos en A y B, respectivamente;
ra y rb= factores de fijeza en A
y B de la columna AB, respectivamente;
y(x)= rotación de la sección transversal debido solamente a
flexión como muestra la fig. 1c;
ya' y yb= rotaciones por flexión
de las secciones transversales en los extremos A' y B' con respecto a la cuerda
A'B', respectivamente;
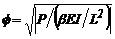 = función de estabilidad en el plano de flexión;
= función de estabilidad en el plano de flexión;
qa y qb= rotaciones de los extremos A y B debido a flexión con
respecto al eje vertical,
respectivamente.
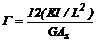 = coeficiente de reducción por cortante.
= coeficiente de reducción por cortante.

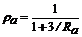 ; y
; y 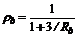 (1a-b)
(1a-b)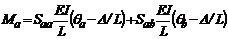 (2a)
(2a)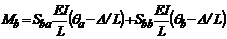 (2b)
(2b)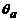 y
y 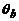 son las rotaciones de los extremos A
y B medidos con respecto la eje inicial del miembro, y D/L el ángulo de rotación de la cuerda del miembro AB. Ambas
rotaciones y momentos en los extremos (Ma y Mb) son positivas en
sentido de las agujas del reloj como se muestra en la
son las rotaciones de los extremos A
y B medidos con respecto la eje inicial del miembro, y D/L el ángulo de rotación de la cuerda del miembro AB. Ambas
rotaciones y momentos en los extremos (Ma y Mb) son positivas en
sentido de las agujas del reloj como se muestra en la 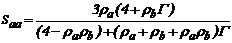 (3)
(3)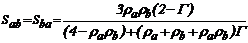 (4)
(4)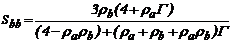 (5)
(5)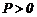 (compresión) o
(compresión) o 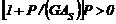
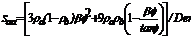 (6)
(6)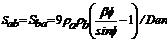 (7)
(7)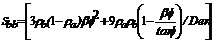 (8)
(8)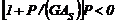
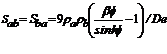 (10)
(10)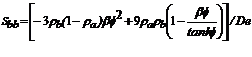 (11)
(11)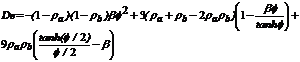 Donde:
Donde:  ; y
; y  .
.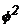 es negativo (i.e.,
es negativo (i.e., 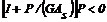 ), los siguientes tres cambios fueron realizados en las ecs. (6)-(8) para
obtener las ecs. (9)-(11): 1) senf por i senhf; 2) tanf por i tanhf; y 3) f por if (donde: i=
), los siguientes tres cambios fueron realizados en las ecs. (6)-(8) para
obtener las ecs. (9)-(11): 1) senf por i senhf; 2) tanf por i tanhf; y 3) f por if (donde: i= 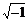 ). Las ecuaciones (2a) y (2b) son derivadas en el Apéndice I.
). Las ecuaciones (2a) y (2b) son derivadas en el Apéndice I.
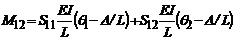 (14)
(14) (15)
(15) (16)
(16)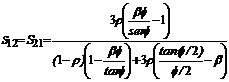 (17)
(17)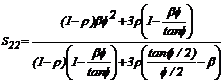 (18)
(18)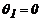 y utilizando las ecs. (14) y (15)
las siguientes expresiones pueden ser obtenidas de las ecs. (12) y (13):
y utilizando las ecs. (14) y (15)
las siguientes expresiones pueden ser obtenidas de las ecs. (12) y (13):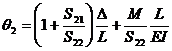 (19)
(19)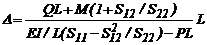 (20)
(20)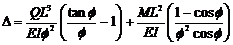 la cual es
la cual es 
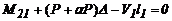 (21)
(21)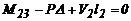 (22)
(22)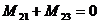 (23)
(23)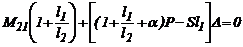 (24)
(24)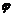 la rotación a flexión del nodo 2 con
respecto al eje horizontal y utilizando las ecs. (2):
la rotación a flexión del nodo 2 con
respecto al eje horizontal y utilizando las ecs. (2):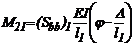 y
y 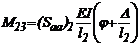
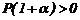 y utilizando las ecs. (6)-(8):
y utilizando las ecs. (6)-(8):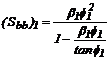 y
y 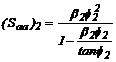
 (25)
(25)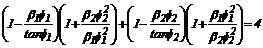 (26)
(26)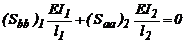
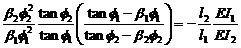 (27)
(27)


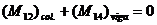 (28)
(28)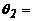
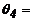 -
- 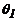 y consecuentemente una sola rotación desconocida y sin deriva entre los
extremos de los miembros), entonces empleando las ecs. (2a) y (2b):
y consecuentemente una sola rotación desconocida y sin deriva entre los
extremos de los miembros), entonces empleando las ecs. (2a) y (2b):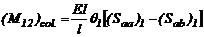 (29)
(29)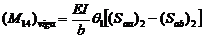 (30)
(30)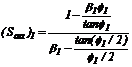 ;
; 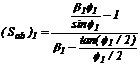 ;
;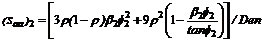 ;
;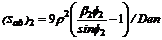 ; y
; y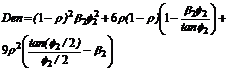
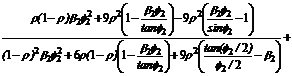
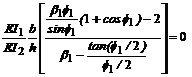 (31)
(31)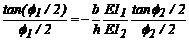


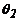 y D se muestras en la
y D se muestras en la 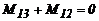 (32)
(32)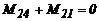 (33)
(33)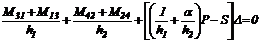 (34)
(34)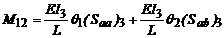 (35)
(35) 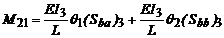 (36)
(36) 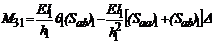 (37)
(37)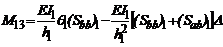 (38)
(38)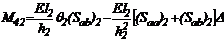 (39)
(39)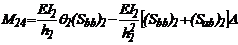 (40)
(40) (41)
(41)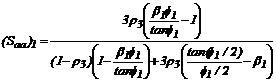 ;
; 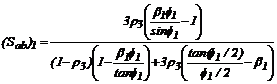 ;
; 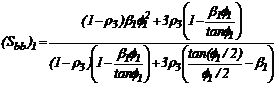 ;
; 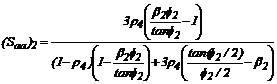 ;
; 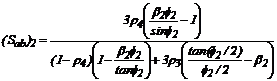 ;
;  ;
; 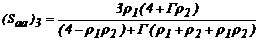 ;
; 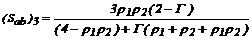 ;
; 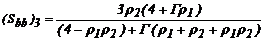 .
.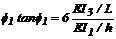 (42)
(42)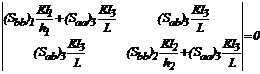 (43)
(43)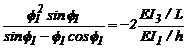 (44)
(44)
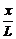 (45a)
(45a)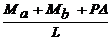 (45b)
(45b)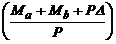 -
- 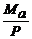 (46a)
(46a)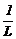
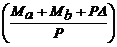 (46b)
(46b)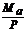 tan(f/2) -
tan(f/2) - 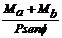 ;
; 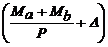 ;
; 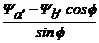 -
- 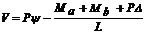 y u'=y +V/(GAs)
y u'=y +V/(GAs)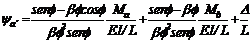 (47a)
(47a)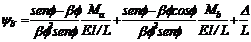 (47b)
(47b)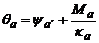 y
y  , respectivamente. Por lo tanto:
, respectivamente. Por lo tanto: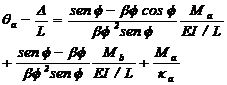 (48a)
(48a)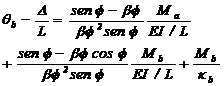 (48b)
(48b)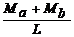 (49b)
(49b)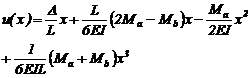 (50a)
(50a)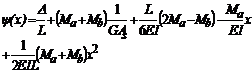 (50b)
(50b)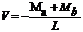 , ya
, ya 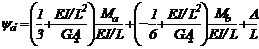 (51a)
(51a)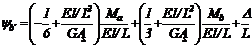 (51b)
(51b)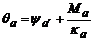 y
y 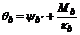 , respectivamente. Por lo tanto:
, respectivamente. Por lo tanto: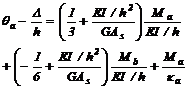 (52a)
(52a)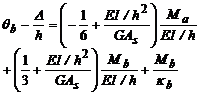 (52b)
(52b)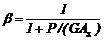 = factor de reducción del la rigidez a flexión causada por la cortante;
= factor de reducción del la rigidez a flexión causada por la cortante;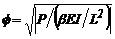 = función de estabilidad en el plano de flexión;
= función de estabilidad en el plano de flexión;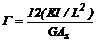 = coeficiente de reducción por cortante.
= coeficiente de reducción por cortante.