
Figure 1. The methodology was applied over a wooden sculpture that has simple and complex curved surfaces
CLOSE RANGE DIGITAL PHOTOGRAMMETRY AND SOFTWARE APPLICATION DEVELOPMENT FOR PLANAR PATTERNS COMPUTATION
FOTOGRAMETRÍA TERRESTRE DIGITAL Y APLICACIÓN SOFTWARE PARA EL DESARROLLO DE PATRONES PLANOS
PEDRO ARIAS
Dep. Natural Resources and Environmental Engineering,
University of Vigo, Spain, parias@uvigo.es
JULIA ARMESTO
Dep. Natural Resources and Environmental
Engineering, University of Vigo, Spain, julia@uvigo.es
JAVIER VALLEJO
Dep. Engineering Design and Technical Projects.
Superior School of Engineering.Bilbao, Spain, eppvamaj@bi.ehu.es
HENRIQUE LORENZO
Dep. Natural Resources and Environmental
Engineering, University of Vigo, Spain, hlorenzo@uvigo.es
Recibido para revisar diciembre 29 de 2008, aceptado abril 13 de 2009, versión final mayo 26 de 2009
ABSTRACT: This paper shows there processes for the particular case of objects with complex surfaces: the 3D modelling of the object and its development to 2D model. The procedure to obtain accurate 3D CAD models of objects with complex surfaces through close range digital photogrammetry is described; several methodological considerations are presented that allow obtaining high accuracy results and minimize processing time. Furthermore a software application that calculates the corresponding planar profiles is developed. The application automatically outputs a CAD neutral file with the definition of the optimized planar patterns needed for the NC cutting machines. The computation of the planar patterns is based on the solution of an optimization problem that takes into consideration the geodesic curvature of the surface of the isoparametric curves.
KEYWORDS: 3D modelling, Close Range Digital Photogrammetry, complex surfaces, cutting profiles.
RESUMEN: Este artículo muestra estos procesos para el caso particular de objetos con superficies complejas: el modelado 3D de objetos y su desarrollo a modelos 2D. Se describe el procedimiento para obtener modelos CAD 3D precisos de objetos con superficies complejas a través de fotogrametría terrestre digital; se realizan varias consideraciones metodológicas que permitirán obtener resultados con alta precisión y minimizado de los tiempos de procesado. Además fue programada una aplicación software para el desarrollo de superficies complejas en el plano. La aplicación proporciona automáticamente archivos CAD estándar, definiendo patrones planos optimizados necesarios para los sistemas CNC. El cálculo de estos patrones planos está basado en la solución de un problema de optimización que tiene en cuenta la curvatura geodésica de las superficies de curvas isoparamétricas.
PALABRAS CLAVE: Modelado 3D, Fotogrametría Terrestre Digital, Superficies Complejas, cutting profiles.
1. INTRODUCTION
The only way European manufacturing companies can succeed in a global marketplace is by implementing newer manufacturing processes that enable them to respond quickly to market changes and provide high quality, low cost products.
Automation is one major step towards achieving the quality, cost and delivery targets. Due to cost effectiveness and quality results, CAD/CAM and CNC machining are replacing the old manual or semi-automated machinery in a wide range of industries. Frequently, it is common that the design drawings corresponding to an object or a prototype to be manufactured through a CNC system are not available. In such cases, reverse engineering techniques must be used in order to generate a 3D digital model of the object. Afterwards, this model is developed to obtain the cutting planar patterns that will allow us to program the CNC machinery operations. The 3D modelling and its development into planar profiles are key processes for the automation and the reliability of this type of manufacturing process when it affects objects with complex surfaces.
The trouble of creating development profiles of 3D surfaces with double curvature to be manufactured at later time by forming planar pieces of metal sheets have been wide treated in the design community of industrial products since it is present in a great variety of industrial areas: automation, aircraft, navigation, boiler-making, inclusive in the textile and the shoe-making industry [1] [2]. The current CNC manufacturing systems along with CAD/CAM systems are becoming one of the major expansion and renovation areas in this type of industries. But the implementation of CNC cutting machinery in the flat sheet manufacturing systems brings serious problems when trying to manufacture complex geometry objects, since defining the optimal form of the cutting profiles, which is essential to program the cutting path, raises serious difficulties. Furthermore, when original design drawings of the objects or prototypes to be manufactured are not available, it is necessary to carry out a previous modelling phase with the purpose to get the precise knowledge of the object geometry and dimensions. The 3D modelling and its development into planar profiles are key processes for the automation and the reliability of this type of manufacturing process when it affects objects with complex surfaces [3].
In recent years, research efforts led to object modelling with complex surfaces in the industrial application fields have been focused on laser scanning technology [4] [5]. However, surface reconstruction from random scanned data usually requires a complex time consuming reconstruction process and significant amount of computation [6]. These considerations have led us to concentrate in evaluating the feasibility of applying digital monoscopic photogrammetry in modelling objects with complex geometry. Some interesting previous works can be found in [7]-[11]. This paper is focused on the monoscopic digital photogrammetry since it has several advantages such as: equipment cost, flexibility, simplicity and calculation volume data processing [12]. In our opinion, these factors make it more viable in industrial applications in terms of cost-efficiency balance point of view than the stereophotogrammetric techniques or single image based processes [13]. Several methodological indications are established that allow us to optimize the time required for the data processing and the final 3D model accuracy.
Furthermore, a custom application has been developed that implements an efficient algorithm for the planar development, for the CAD model obtained from the photogrammetric procedure. This application allows us to obtain a CAD file that has the definition of the optimum cutting profiles of the curved surfaces. The mathematical principles of this application are shown. The method is applied over a wooden sculpture that has simple and complex curved surfaces (see figure 1).

Figure 1. The methodology was applied over a wooden
sculpture that has simple and complex curved surfaces
2. METHOD
2.1 Photogram Metric Procedure: 3D Modelling
Close range photogrammetry
basically involves the use of a network of photographs of an object taken from
different angles. In our case study, the photography network was designed
considering the parameters that determine the strength of the geometry according
to [14]. A digital calibrated camera, Canon EOS 10D of 6.291.456 pixels CCD
resolution was used. The interior orientation parameters are showed in table 1.
Table 1. Interior orientation
parameters of the camera used The sculpture was placed on a
supported base covered by a
10
cm grid (see figure 2).
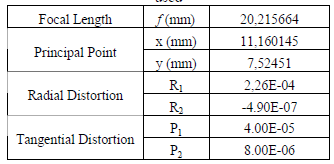

Figure 2. The wooden sculpture was placed on a supported
base covered by a
10 cm
grid
As photogrammetric system we have used a monoscopic digital photogrammetric software, the package Photomodeler Pro 5.0 [15]. The system is used for the digital orientation and restitution of photographs. It enables us to work with pictures obtained either with digital cameras. The results obtained can be of two types: numeric for quality control of results (in ASCII format) and graphic (DXF, 3D Studio, RAW, 3dm and Iges).
The cross points within the grid and the sculpture vertex are taken as target points for the camera poses computation. Additionally, a grid of dots set at 5 cm among them was projected over the complex curved surfaces for inner point restitution. The photographs were taken all around the object from a distance of 1 meter, keeping the convergence of rays at 40º to 90º.
The image measurement was made as a manual process for the identification of common pixels in different images in the external orientation, as well as in the line drawing (points and lines). The process of image measurement was automatic from grid of dots set projected over the complex curved surfaces. The inner points in this kind of surfaces (and due the texture of the model) were calculated using a structure light system. The photogrammetric system used has implemented algorithms to calculate Cartesian coordinates of the grid of dots set with shape of circle or ellipse. The structure light system was builded using a little searchlight with a grid of dots built-in.
The problem of obtaining a digital model that properly defines the geometry of the object from digital images can be stated as follows: (Xi, Yi, Zi) of a set of n points within the object surface must be calculated in a common Cartesian system given the image coordinates (xi, yi); then a surface S might be found that approximates or interpolates the set of points.
There is a perspective relationship between the 3D co-ordinates in the object space and the 2D corresponding coordinates in the image plane, since an image point i’ (xi, yi, -f), the perspective centre O of the camera (Xo, Yo, Zo) and the object point i (Xi, Yi, Zi), are over the same line i’oi. This relationship can be written mathematically according to equation (1).
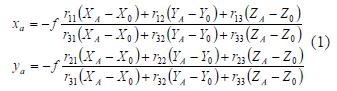
Where (x, y) are image co-ordinates of target points, f, the principal distance; (X, Y, Z) are object space co-ordinates of target points; (X0, Y0, Z0) are object space co-ordinates of the projection centre; rij are the components of the rotation matrix R, which is a function of the three rotation angles ω, κ, φ that define the spatial rotation between the object space system to the image co-ordinate system.
The photogrammetric model generation involves the previous computation of the six orientation parameters corresponding to the position (space co-ordinates) and orientation (rotation angles) of the camera projection centre in a Cartesian coordinate system for each image plane. For this end, the target points in the object space are matched with the corresponding ones in the image planes of the network. If a number enough of target points are used, the six unknowns for each image plane can be found. Generally more than the necessary minimum are used and the parameters are estimated by the bundle adjustment functional model, which is based on least squares estimation (for further information see [16]).
The bundle adjustment procedure was carried out using, 12 control points located on the supported base that allowed to scale the 3D model and to fix the reference system, 17 images in digital format of the sculpture. After the bundle adjustment the photogrammetric system used to gauge project quality the value called σ0 (or more properly a priori σ0), calculated like the variances of the residuals. The value of σ0 was estimated in 0.85 pixels.
The computation of the spatial 3D co-ordinates of the object vertexes and the projected dots within the doubly curved surface is analogue to the method described for the camera poses calculation, see equation (2).
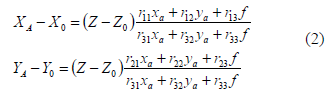
Now the unknowns are the co-ordinates (XA, YA, ZA) of the points, and they are computed given the corresponding (xa, ya) image co-ordinates and the co-ordinates and rotation angles of the camera projection centre, which were obtained for each image plane in the prior stage. In order to achieve enough level of redundancy measurements, which is essential for obtaining high accuracy results according to [14], more than three images were used for the restitution of each point. The system is also solved by bundle adjustment, in this last process the photogrammetric system allow us to adjust together the co-ordinates of the grid of dots set with the exterior orientation parameters.
The photogrammetric software used is a convergent monoscopic multistation, this system is based in a process of intersection of rays common for the calculate of co-ordinates. This process is used for the restitution of all points, including the grid of dots.
Reconstruction of flat surfaces is performed by fitting a flat surface to sets of coplanar points and edges, in such a way that the normal distance from the surface to the vertexes is minimized. Constrictions concerning parallel and perpendicular conditions of edges are previously established in order to minimize errors in the points restitution process. For the reconstruction of the curved surfaces a Delaunay triangulation is performed that approximates them. The triangular mesh is then smoothed in order to get a better fitting with the original surface.
2.2 Surface Flattening Method
The
procedure implemented here and
described in points 2.2.2 and 2.2.3, is based on the Azariadis and
Aspragathos method (see [17], [18] for details).
2.2.1 Application plug-in development
The
computation of the planar profiles of the developed surfaces starts from the 3D
model definition obtained as result of the photogrammetric process. The faces
of the model defined with developable surfaces (Gaussian curvature = 0) are
easily developed using the functionality of a commercial CAD application.
However, this is not possible for the faces with doubly curved geometry that
cannot be flattened into a map without stretching, tearing, or compressing
itself. When Gaussian curvature is not very high, an optimization procedure
could be proposed that provides a fair approximation to the shape of the planar
pattern minimizing the deformation of the plate.
The mathematics of this method takes into account the isometric development of the isoparametric curves with geodesic curvature preservation. Manipulation and complex data computation of model geometry was required therefore the application for planar patterns computation was conceived as a custom plug-in to a CAD application. A plug-in is a software module that extends the functionality adding new commands or features to the application.
The application plug-in was developed with the Rhino 3.0 SDK, an API that allows the access to the functions of Rhinoceros 3.0 CAD application. This plug-in is build with Microsoft Visual C++ 6.0 as a Windows DLL (Dynamic Link Library) that could be executed from Rhino’s command line.
A neutral file of the model is generated in order to manage its geometry into the CAD application. Rhino’s SDK provides all the functionality needed to select the surface patches and access the data structure of the model, computing position, normal and tangent vectors, needed for the mathematical procedure
The resulting planar pattern obtained with the plug-in is a geometrical entity of the CAD application and can be exported in different formats of CAD standard neutral files.
2.2.2 Mesh definition
The mesh
development procedure that is applied is based on the development of one of the
families of isoparametric curves. Therefore, the surface is accurately
approximated by a set of flat triangular elements that are homogeneously
distributed. This means that their vertexes are placed at the intersection of a u-isoparametric curve and a v-isoparametric curve of the x= f(u, v) surface. Each strip of
triangles is defined between two u-
or v-isoparametric curves that are
approximated by the set of triangle sides with vertices on the same curve.
2.2.3 Isometric mapping of a surface curve with
geodesic curvature preservation
The
second stage consists of an initial estimation of the mesh development. One set
of isoparametric curves is developed preserving the length of the curve between
each two points (isometric map) and the geodesic curvature. This criterion is
essential since it guarantees the uniqueness of the resulting curve. The
development procedure of a curve C lying
on a surface requires the approximation by a finite set of points Ci taken on the curve. The
tangent plane Ti and the
normal vector Ni to the
surface has to be known at each of these points. The curve C is isometricly mapped onto a planar curve C* making the chord lengths of C* the same as the distance between the corresponding points of C. The geodesic curvature of C is preserved at each intermediate
point Ci if we keep the
angle θi between two
successive chords (Ci-1*, Ci*,
Ci+1*) of the planar curve C* the same as the angle defined by the projections onto the tangent plane Ti of the segments (Ci-1, Ci, Ci+1).
In the triangular mesh of the surface, the sides of the triangles that join the vertexes lying on these curves approximate the u- and v-isoparametric curves. The first estimation of the developed mesh is obtained applying an isometric map to these lines with geodesic curvature preservation. By carrying out this procedure, developable surfaces are flattened without distortions, while a distorted flattened mesh is obtained in the case of doubly curved surfaces.
2.2.4 Reduction
of the distortions: an energy based method
The
development of the surface approximate triangulation may be expressed by the
same procedure applied to the mapping of one unique curve. Isometric mapping
requires the preservation of the distances between pairs of nodes measured on
the 3D mesh. It should be taken into account that each node of the
triangulation lies on the crossing point of two u- and v-isoparametric
surface curves. Preservation of the geodesic curvature at each mesh node
requires the angle to be preserved between the projected segments of each one
of the isoparametric curves and also the relative angle between them.
If the surface is doubly curved, it is not possible to preserve the geodesic curvature and the isometric map, therefore the planar development of the mesh will have an error. To estimate this error an energy function is proposed. This function combines two main error components. The first error term estimates the error due to the distance difference between the nodes in the 3D mesh and the corresponding nodes in the planar development. The second term estimates the angular distortion between the isoparametric curves at each node.
3. RESULTS
3.1 3D Modelling: Photogrammetric Procedure
The 3D
surfaces modeling was obtained with 74 restituted points (including the
projected grid of dots). The bundle adjustment provide the results show in the
table 2, for all points (including the grid of dots) used to generate the 3D
model. This table shows information about: standard deviation of the cloud of
points (average values in X, Y, Z axes and quadratic composition of the
averages); the mean quadratic error, the mean error and the maximum error
observed in the parallax (m); Root Mean Square (RMS) error and maximum residual
error (pixels); angle maximum and minimum between images (deg).
Table 2. 3D model accuracy
assessment: standard deviation (m) of the cloud of points (average values in X,
Y, Z axes and quadratic composition); the mean square error, the mean error and
the maximum error observed in the parallax (m); Root Mean Square error and
maximum residual error (pixels); angle maximum and minimum between images (deg)

The use of a flat grid as support base for the object simplifies the processing stage, since the point identification on a 2D surface is significantly less affected by visual perception errors than the identification of 3D points. The generation of the 3D surface model through digital monoscopic photogrammetry has shown to be a straightforward, fast and reliable method when developable surfaces are surveyed (see figure 3). In the case of complex surfaces, the use of the projected grid of dots has shown to be a simple and affordable system that provides high accuracy results (see table 2).
Figure 3. Wire-frame 3D model of the wooden sculpture
Nevertheless we must point out that the effectiveness of this method depends on the size of the object and the complexity of the surface, since the larger and/or the more complex it is, the higher number of dots might be projected and processed to warrantee the match between the 3D digital model and the prototype.
3.2 Surface
Flattening Method
A custom Rhino plug-in application that
obtains the planar development of doubly curved surfaces starting from the CAD
definition of the surfaces has been developed and implemented.
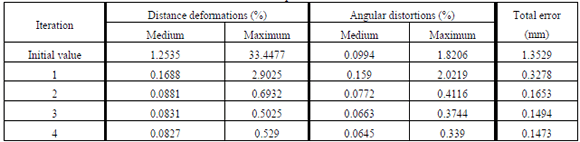
The application generates a CAD neutral file with the shape of the cutting profile that is needed for the machining processes of the metal sheets (see figure 4). The mathematics of this method is based on the solution of an optimization problem that takes into account the isometric development of the isoparametric curves with geodesic curvature preservation. The surface is first approximated with a triangular mesh. Distance deformations and angular distortions are measured between each pair of mesh nodes and each pair of crossing isoparametric curves at the nodes respectively, are observed as a result of the mesh flattening process. An optimization procedure is applied to a function based on the value of these deformations. Table 3 shows the evolution of these values in successive iterations, where the values of distance deformations and angular distortions are expressed as a percentage of the actual distances and angles. The medium and the maximum values are computed each iteration.
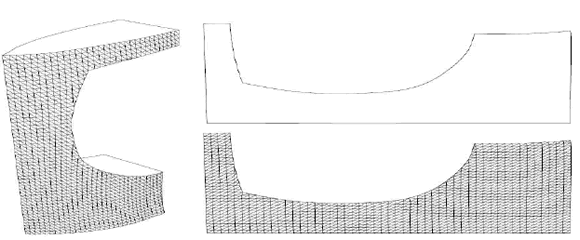
Figure 4. 3D model of the grid surface with a doubly
curved surface (left), plannar development of the grid (up
right) and cutting profile (down right)
Table 3. Results of the
minimization development method used on double curved surfaces
4. CONCLUSIONS
In this paper an approach to the application of digital monoscopic photogrammetry technique in the 3D modelling of doubly curved objects is presented, a surface flattening method, based on isometric mapping and geodesic curvature preservation, is implemented as a CAD application plug-in, and finally, an iterative energy based optimization procedure is applied that minimises distortions in the final planar profiles.
The use of Photogrammetric procedures in this kind of industrial applications has shown some advantages from other classical methodologies, could be appointed:
For other side, we can see same aspects or characteristics would have to be more developed, for example:
In conclusion, two main contributions should be highlighted. Digital photogrammetry has shown to be a feasible and affordable tool in the accurate 3D model generation of complex objects; it is relevant that both of the aspects of feasibility and affordability are decisive factors in the accomplishment of automated manufacturing processes. Then the 3D model is saved to a neutral file format that could be processed with a CAD application. The surface flattening method is implemented as a customized plug-in. The proposed development and optimization methods have been proven to be effective and highly efficient in the case study. Finally, the resulting planar pattern is then saved to a neutral file that could be accessible from a wide number of different machine tool programming applications.
5. ACKNOWLEDGMENTS
This article is part of a research project financed by Ministry Education and Science “Utilizacion de tecnicas geomaticas para el analisis dimensional-estructural y conservacion de puentes historicos singulares” (BIA2006-10259).
REFERENCES
[1] KARUNAKARAN, K.P., AGRAWAL, S., VENGURLEKAR,P.D., SAHASRABUDHE, O.S., PUSHPA,.V. AND ELY, R. Segmented object manufacturing. IEEE Transactions, 39, 291-302, 2005.
[2] ARIAS, P., ARMESTO, J., LORENZO, H. AND ORDOÑEZ, C. 3D terrestrial laser technology in sporting craft 3D modelling. International Journal of Simulation Modelling, 6 (2), 65-72, 2007.
[3] CUARTAS, E AND PRIETO, F. Reconstrucción de objetos con superficies Tipo 2-variedad diferenciable. Dyna, 156 (75), 7-18, 2008.
[4] RABBANI, T., DIJKMAN, S., VAN DEN HEUVEL, F. AND VOSSELMAN, G. An integrated approach for modelling and global registration of point clouds. ISPRS Journal of Photogrammetry and Remote Sensing, 61 (6), 355-370, 2007.
[5] ROCA-PARDIÑAS, J., LORENZO, H., ARIAS, P. AND ARMESTO, J. From laser point clouds to surfaces: Statistical nonparametric methods for three-dimensional reconstruction. Computer Aided Design, 40 (5), 646-652, 2008.
[6] YAU, H.T., LEE, R.K., CHUANG, C.M. AND HSU, C.Y. NC Tool-Path Generation Based on Surfel Models Constructed from Random Scanned Data. Computer-Aided Design & Applications, 2 (1-4), 567-576, 2005.
[7] Y. ZHANG. Measurement of industrial sheetmetal parts with CAD, designed data and nonmetric image sequence. Proceedings of the XXth ISPRS Congress Commission 5, Istanbul, Turkey , 2004.
[8] TANGELDER, J.W.H., ERMES, P., VOSSELMAN, G. AND VAN DEN HEUVEL, F.A. CAD-based photogrammetry for reverse engineering of industrial installations. Computer-Aided Civil and Infrastructure Engineering, 18, 264-274, 2003.
[9] BOSEMANN, W. Advances in photogrammetric measurement solutions. Computers in Industry, 56 (8-9), 886-893, 2005.
[10] ERGUN, B. An expert measurement system for photogrammetric industrial application. Measurement, 39 (5), 415-419, 2006.
[11] D'ANGELO, P., WOHLER, C. Image-based 3D surface reconstruction by combination of photometric, geometric, and real-aperture methods. ISPRS Journal of Photogrammetry and Remote Sensing, 63 (3), 297-321, 2008.
[12] ARIAS, P., CAAMAÑO, J.C., LORENZO, H. AND ARMESTO, J. 3D Modeling and Section Properties of Ancient Irregular Timber Structures by Means of Digital Photogrammetry. Computer-Aided Civil and Infrastructure Engineering, 22 (8), 597-611, 2007.
[13] SALAZAR, A., SÁNCHEZ, L.G. AND PRIETO, F. Sistema de adquisición de imágenes de rango con base en estéreo-activo. Dyna, 153 (74), 301-311, 2007.
[14] MASON, S.O. Conceptual Model of the convergent multistation network configuration task. Photogrammetric Record, 15 (86), 277-299, 1995.
[15] EOS SYSTEMS INC. Photomodeler Pro 5.0. User manual. Vancouver, Canada, 2003.
[16] COOPER, M. AND ROBSON, S.. Theory of Close Range Photogrammetry, In: Close Range Photogrammetry and Machine Vision (Ed. K.B.Atkinson), Whittles Publishing, 9-51, 2001.
[17] AZARIADIS,P. AND ASPRAGATHOS, N. Design of plane patterns of doubly curved surfaces. Computer-Aided Design, 29 (10), 675-85, 1997.
[18] AZARIADIS,P. AND ASPRAGATHOS, N. Geodesic curvature preservation in surface flattening through constrained global optimization. Computer-Aided Design, 33, 581-591, 2001.