REPRESENTACIÓN DE SISTEMAS NO LINEALES Y DIAGNÓSTICO DE FALLAS BASADO EN UN ENFOQUE MULTI-MODELOS
NONLINEAR SYSTEM REPRESENTATION AND FAULT DIAGNOSIS BASED ON A MULTI-MODELS APPROACH
MANUEL
ADAM MEDINA
Centro Nacional de Investigación y Desarrollo Tecnológico,
Cuernavaca Morelos, México, adam@cenidet.edu.mx
DIDIER THEILLIOL
Centre de Recherche en Automatique
de Nancy, Vandoeuvre, France
CARLOS MANUEL ASTORGA ZARAGOZA
Centro Nacional de Investigación y
Desarrollo Tecnológico, Cuernavaca Morelos, México, astorga@cenidet.edu.mx
LUIS GERARDO VELA VALDÉS
Centro Nacional de Investigación y
Desarrollo Tecnológico, Cuernavaca Morelos, México, velaluis@cenidet.edu.mx
GERARDO
VICENTE GUERRERO RAMÍREZ
Centro Nacional de Investigación y Desarrollo
Tecnológico, Cuernavaca Morelos, México, gerardog@cenidet.edu.mx
Recibido para revisar septiembre 30 de 2008, aceptado noviembre 21 de 2008, versión final diciembre 12 de 2008
RESUMEN: En este artículo se desarrolla un método para la representación de sistemas no lineales, así como un esquema de diagnóstico de fallas; en donde ambos utilizan un enfoque multi-modelos. El comportamiento dinámico del sistema se describe mediante el uso de diferentes puntos de operación por cada modelo lineal invariante en el tiempo. Por cada modelo un filtro de Kalman desacoplado de fallas es utilizado. Esto permite la generación de un banco de residuos con la finalidad de estimar funciones de ponderación robusta a fallas. Estas últimas se enlazan directamente al esquema de detección, localización y estimación de fallas con objeto de mejorar su eficacia. Finalmente, se realiza un ejemplo de simulación a fin de probar el desempeño del método desarrollado.
PALABRAS CLAVE: Representación Multi-Modelos, detección, localización y estimación de fallas, Filtro desacoplado de Fallas.
ABSTRACT: In this article are developed a method for the representation of nonlinear systems as well as a scheme of fault diagnosis, both use a multi-model approach. The dynamic behavior of the system is described using different points of operation for every linear time invariant model. For every model a decoupled Kalman filter of faults is used. This allows the creation of a bank of residuals to estimate the robust weighting functions. This bank is directly linked to a scheme for detecting, isolating and estimating faults in order to improve its effectiveness. A simulation example to test the performance of the developed method is presented.
KEYWORDS: Fault detection and isolation; Multi-models; Decoupling filter.
1. INTRODUCCIÓN
Los sistemas industriales automatizados complejos son vulnerables a fallas en instrumentación como sensores, actuadores o componentes. La detección y localización de fallas (FDI, por su acrónimo en inglés Fault Detection and Isolation) ha sido desarrollada tradicionalmente con un enfoque basado en modelos usando modelos lineales o linealizados. Diversos artículos han sido publicados a este respecto; estos trabajos condujeron a métodos robustos a incertidumbres paramétricas y a errores de modelado del sistema, cuando el ruido está o no presente [1], [2] y [3]. Cuando el rango de operación del sistema se expande, el modelo linealizado ya no es capaz de representar la dinámica del sistema. Con la creciente complejidad de los sistemas de ingeniería moderna y el aumento en la demanda por la seguridad y confiabilidad, se ha despertado un gran interés en el desarrollo de métodos de localización y detección de fallas (FDI).
Los problemas de la FDI han sido resueltos usando observadores no lineales. Estos observadores han sido propuestos bajo el enfoque analítico en [4] y el enfoque geométrico en [5], éstos requieren de un conocimiento adecuado de los sistemas no lineales. En la práctica, los procesos industriales como son: minería, química, tratamiento de agua, etc., están caracterizados por ser procesos complejos que operan en múltiples regiones de operación. A menudo es difícil obtener modelos no lineales que describan exactamente plantas en todos los regímenes.
Generalmente, los sistemas no pueden ser modelados mediante modelos matemáticos explícitos. Para resolver este problema, algunos métodos basados en la representación de sistemas no lineales emplean la descomposición de éstos en un conjunto de modelos lineales. Esta estructura es considerada como modelos múltiples (MM) [6]. En sistemas no lineales, la estructura de MM ha sido propuesta para el dominio del control. La técnica de MM permite la FDI, cuando los sistemas NL son modelados alrededor de un punto de operación [7] ó cuando el sistema está definido como un sistema híbrido lineal [8]. En este trabajo, se considera el enfoque MM en el mismo contexto que en [1], utilizando el método estadístico desarrollado en [7]. El enfoque multi-modelo ha sido a menudo usado en años anteriores para el modelado y control de sistemas no lineales [9]. Se han propuesto algunos métodos basados en redes neuronales, como el mostrado en [10]. En [11], desarrolló una estrategia multi-modelo en donde cada modelo representa una falla particular en el sistema. Los enfoques multi-modelo en sistemas industriales para diagnóstico de fallas [5] y para efectos de control [3][12] han sido demostrados considerando la hipótesis de que las funciones de ponderación de los modelos no están afectadas por fallas. Un enfoque multi-modelo para el caso de fallas usa filtros de Kalman desacoplados, espacios de paridad, observadores politópicos con entradas desconocidas [20][13] donde la FDI se representa tomando en cuenta la función de ponderación activa basada en la metodología que se presenta en este trabajo. Las funciones de ponderación son importantes en las múltiples técnicas de control tales como en la estrategia de ganancia programada [14] o en controladores interpolados [4] o en controladores conmutados [10]; sin embargo, estos métodos no se ocupan tanto de regímenes de operación múltiples y de fallas. El objetivo de este trabajo es diseñar un esquema que permita la FDI y la ponderación de cada modelo robusto en el contexto de MM. Para alcanzar este propósito se desarrolla un banco de filtros de Kalman desacoplados basados en la interpolación de modelos múltiples. Este banco se diseña con el fin de que el vector de residuos pueda ser separado en dos partes: uno insensible y otro sensible a las fallas. El método multi-modelo propuesto permite determinar tanto el régimen de operación como la falla en cada muestra.
2. FUNCION DE PONDERACIÓN ROBUSTA
2.1 Modelado
del Sistema en Caso de Falla
Considerar un sistema dinámico no lineal en tiempo discreto descrito
por
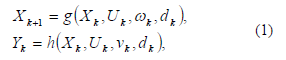
donde 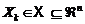 representa el
vector de estado,
representa el
vector de estado, 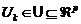 el vector de entrada,
el vector de entrada,  el vector de salida,
el vector de salida,  el vector de
falla y las matrices
el vector de
falla y las matrices  y
y  son dos ruidos
blanco de media cero independientes con matrices de varianza – covarianza
definidas, respectivamente, por
son dos ruidos
blanco de media cero independientes con matrices de varianza – covarianza
definidas, respectivamente, por 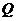 y
y  . Las funciones g y h se suponen que son continuamente
diferenciables en X y U.
. Las funciones g y h se suponen que son continuamente
diferenciables en X y U.
Definición 1. En ausencia de falla 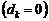 [15].
[15].
Dado un conjunto U, un punto 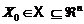 es un punto de
equilibrio del sistema (1) si una entrada de control
es un punto de
equilibrio del sistema (1) si una entrada de control 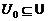 existe tal que
existe tal que 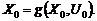 Llamamos un
conjunto conectado de puntos de equilibrio una superficie de equilibrio. Suponga
que
Llamamos un
conjunto conectado de puntos de equilibrio una superficie de equilibrio. Suponga
que 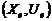 es un punto en
una superficie de equilibrio y define un cambio de estado
es un punto en
una superficie de equilibrio y define un cambio de estado 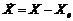 y un cambio de
entrada
y un cambio de
entrada 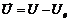 , el sistema no lineal (1) con respecto a
, el sistema no lineal (1) con respecto a 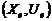 puede ser
expresado como
puede ser
expresado como
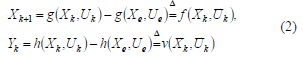
Basada en definiciones previas, se asume que el comportamiento dinámico
del sistema en diferentes puntos de operación puede ser aproximado por un
conjunto de M modelos lineales
invariantes en el tiempo (LIT) como el propuesto por [9], [15], o [16]. Por lo
tanto, los sistemas dinámicos tales como sistemas no lineales, sistemas
lineales variantes en el tiempo, sistemas lineales por etapas pueden ser
representadas por una descomposición de los rangos de operación completa dentro
de un número de posibilidades de traslaparse los regímenes de operación [14], [13].
Para cada régimen, se define un sistema lineal local como [9]. Consecuentemente
la representación de espacio de estado de un sistema alrededor del j-ésimo punto de operación  con fallas
aditivas bajo suposiciones estocásticas, se describe como sigue:
con fallas
aditivas bajo suposiciones estocásticas, se describe como sigue:
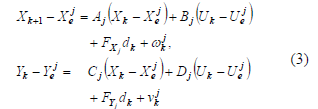
Las matrices invariantes 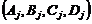 son definidas
alrededor del j-ésimo punto de
operación
son definidas
alrededor del j-ésimo punto de
operación  , generalmente obtenido de una expansión de Taylor de
primer orden alrededor de
, generalmente obtenido de una expansión de Taylor de
primer orden alrededor de 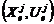 o por identificación
de un sistema no lineal alrededor de puntos de operación predefinidos [17]. Suponiendo
que cada punto de operación es bien elegido tal que las matrices de estado son
diferentes en cada punto de operación. Esto se realiza correctamente en cuanto
al punto de vista económico y de productividad. Por lo tanto, los modelos para
cada punto de operación son suficientemente diferentes y esto permite generar los
diferentes residuos en el esquema FDI. Las matrices
o por identificación
de un sistema no lineal alrededor de puntos de operación predefinidos [17]. Suponiendo
que cada punto de operación es bien elegido tal que las matrices de estado son
diferentes en cada punto de operación. Esto se realiza correctamente en cuanto
al punto de vista económico y de productividad. Por lo tanto, los modelos para
cada punto de operación son suficientemente diferentes y esto permite generar los
diferentes residuos en el esquema FDI. Las matrices 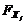 y
y 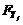 son matrices de distribución de fallas en actuador y
en sensor, respectivamente. Las matrices
son matrices de distribución de fallas en actuador y
en sensor, respectivamente. Las matrices 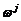 y
y  son dos ruidos
blancos de media cero independientes con matrices de varianza – covarianza
definidas, respectivamente, por
son dos ruidos
blancos de media cero independientes con matrices de varianza – covarianza
definidas, respectivamente, por 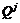 y
y  . Sin pérdida de generalidad,
. Sin pérdida de generalidad, 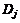 se supone ser
igual a cero y de acuerdo a [18], en presencia de fallas en sensores, actuadores
o componentes, el sistema representado mediante el espacio de estado previo
definido en (3) puede ser equivalente a:
se supone ser
igual a cero y de acuerdo a [18], en presencia de fallas en sensores, actuadores
o componentes, el sistema representado mediante el espacio de estado previo
definido en (3) puede ser equivalente a:

con  y
y 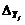 como vectores
constantes que dependen del j-ésimo
modelo lineal tal como:
como vectores
constantes que dependen del j-ésimo
modelo lineal tal como:
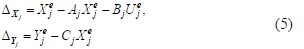
La matriz de distribución de la falla está representado por 
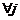 . Alrededor del j-ésimo punto de operación, se asume
que
. Alrededor del j-ésimo punto de operación, se asume
que  Este sistema
lineal puede ser especificado por el siguiente conjunto de matrices del
sistema:
Este sistema
lineal puede ser especificado por el siguiente conjunto de matrices del
sistema:

Esto, permite definir  que es una secuencia
matricial cambiando dentro de un conjunto convexo, definido como
que es una secuencia
matricial cambiando dentro de un conjunto convexo, definido como

Así,  caracteriza en
cada muestra al sistema tal como se propone en ausencia de falla [16] y con
fallas [1]. Consecuentemente, el comportamiento dinámico del sistema está
definido por un conjunto convexo de multi-modelos LIT
caracteriza en
cada muestra al sistema tal como se propone en ausencia de falla [16] y con
fallas [1]. Consecuentemente, el comportamiento dinámico del sistema está
definido por un conjunto convexo de multi-modelos LIT 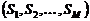 . La representación de espacio de estado (4) bajo un
conjunto convexo (7) puede ser considerado como un enfoque de modelado
convencional para la planta no lineal suave donde
. La representación de espacio de estado (4) bajo un
conjunto convexo (7) puede ser considerado como un enfoque de modelado
convencional para la planta no lineal suave donde  es una función
de ponderación apropiada que incorpora las no linealidades de la planta.
es una función
de ponderación apropiada que incorpora las no linealidades de la planta.
2.2 Ubicación del Problema
Los sistemas a considerar pueden ser descritos por una representación
multi-modelo. En este artículo, sólo se usará la representación multi-modelo, en
donde se asume con precisión el modelo del comportamiento del sistema. Como el
propuesto en [4] y [9], un banco de filtros de Kalman clásicos pueden ser diseñadas
para obtener una estimación de  . Con esta suposición, el sistema evoluciona en torno
al j-ésimo punto de operación, un i-ésimo filtro de Kalman (
. Con esta suposición, el sistema evoluciona en torno
al j-ésimo punto de operación, un i-ésimo filtro de Kalman (  que representa
el número de filtros de Kalman) se describe por
que representa
el número de filtros de Kalman) se describe por
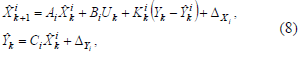
donde 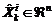 denota el
vector de estado estimado y
denota el
vector de estado estimado y 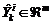 es la estimación
de la salida obtenida del filtro lineal basado en el i-ésimo modelo lineal.
es la estimación
de la salida obtenida del filtro lineal basado en el i-ésimo modelo lineal. 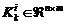 es la matriz de
ganancia del filtro de Kalman. El índice j representa al sistema y el índice i está dedicado a los modelos para los filtros.
es la matriz de
ganancia del filtro de Kalman. El índice j representa al sistema y el índice i está dedicado a los modelos para los filtros.
Este banco de filtros de Kalman permite obtener el error de estados estimado  y los vectores de
residuos de salida
y los vectores de
residuos de salida 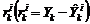 . Cuando ocurre una falla y el régimen de operación no
cambia (i.e. cuando
. Cuando ocurre una falla y el régimen de operación no
cambia (i.e. cuando  y
y 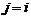 ), la diferencia entre la representación del sistema
(4) y los filtros (8) está representada como sigue:
), la diferencia entre la representación del sistema
(4) y los filtros (8) está representada como sigue:
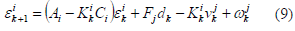
y la estimación del error de salida

En ausencia de fallas, el vector de estimación del error se escribe
como 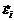 y el vector de
salida residual se denota como
y el vector de
salida residual se denota como 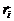 . En ausencia de falla, el residuo generado por el i-ésimo filtro se supone a tener una
distribución Gaussiana con media cero (denotado por
. En ausencia de falla, el residuo generado por el i-ésimo filtro se supone a tener una
distribución Gaussiana con media cero (denotado por 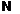 ). Este residuo
permite evaluar la validez de cada modelo lineal. En [4] consideran el vector de
residuos para determinar la probabilidad de cada modelo lineal tomando en
cuenta las mediciones previas de acuerdo a la teoría de probabilidad de Bayes. Los
residuos estacionarios permiten una función de distribución de probabilidad,
notada
). Este residuo
permite evaluar la validez de cada modelo lineal. En [4] consideran el vector de
residuos para determinar la probabilidad de cada modelo lineal tomando en
cuenta las mediciones previas de acuerdo a la teoría de probabilidad de Bayes. Los
residuos estacionarios permiten una función de distribución de probabilidad,
notada 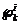 , definida como
, definida como

donde 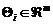 es la matriz de
covarianza de los residuos
es la matriz de
covarianza de los residuos  . Basado en la función de distribución de
probabilidad, un modo de probabilidad, notado como
. Basado en la función de distribución de
probabilidad, un modo de probabilidad, notado como 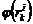 , puede ser calculado como
, puede ser calculado como 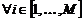
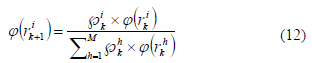
Por lo tanto, el modo de probabilidad del algoritmo de estimación puede
obtenerse para cada modelo. Cuando la probabilidad converge a uno, los otros
modelos convergen a cero. Este modo de probabilidad estimado por cada modelo se
considera como la función de ponderación respectiva a cada modelo. En presencia
de fallas, la siguiente evaluación puede ser establecida  :
:

Una primera suposición ha sido establecida previamente. Cada modelo es
diferente de cada uno, así solo un residuo  puede seguir
una distribución Gaussiana normal cuando j=i.
Cuando
puede seguir
una distribución Gaussiana normal cuando j=i.
Cuando 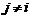 , la diferencia entre la representación del sistema
(4) con
, la diferencia entre la representación del sistema
(4) con  y el filtro de
Kalman (8) con
y el filtro de
Kalman (8) con  conducen a un residuo diferente de (13), i.e.
conducen a un residuo diferente de (13), i.e. 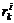

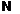 para
para 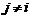 con cualquier d.
De otra manera, cuando
con cualquier d.
De otra manera, cuando 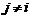 , la diferencia entre la representación del sistema y
el filtro de Kalman conducen a:
, la diferencia entre la representación del sistema y
el filtro de Kalman conducen a:
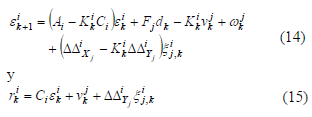
donde  corresponde a
la magnitud de los errores de modelado entre el sistema representado por el j-ésimo modelo lineal y el i-ésimo modelo lineal usado para el
cálculo del filtro de Kalman.
corresponde a
la magnitud de los errores de modelado entre el sistema representado por el j-ésimo modelo lineal y el i-ésimo modelo lineal usado para el
cálculo del filtro de Kalman. 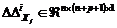 y
y  son las
matrices de distribución del error de modelado asociada a la ecuación de estado
del sistema y a la ecuación de salida, respectivamente. Las dimensiones de
son las
matrices de distribución del error de modelado asociada a la ecuación de estado
del sistema y a la ecuación de salida, respectivamente. Las dimensiones de 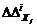 y
y  están directamente vinculadas con el error de modelado
procedentes de las matrices
están directamente vinculadas con el error de modelado
procedentes de las matrices 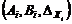 y
y  , respectivamente. El uso de los filtros de Kalman
permiten las siguientes propiedades residuales
, respectivamente. El uso de los filtros de Kalman
permiten las siguientes propiedades residuales  :
:
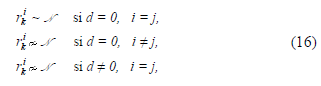
Cuando  , el algoritmo proporciona funciones de ponderación
tales que
, el algoritmo proporciona funciones de ponderación
tales que 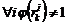 pero
pero 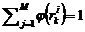 . El método de interpolación entre los diferentes
puntos de operación y las funciones
. El método de interpolación entre los diferentes
puntos de operación y las funciones 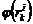 puede tomar
algunos valores entre 0 y 1 expresando el porcentaje valido de un modelo en
cuanto al comportamiento dinámico del sistema (7). De acuerdo a (16),
la FDI no se obtiene
correctamente, ya que el vector de residuos es corrompido al mismo tiempo por
cambio en los puntos de operación y la presencia de las fallas.
puede tomar
algunos valores entre 0 y 1 expresando el porcentaje valido de un modelo en
cuanto al comportamiento dinámico del sistema (7). De acuerdo a (16),
la FDI no se obtiene
correctamente, ya que el vector de residuos es corrompido al mismo tiempo por
cambio en los puntos de operación y la presencia de las fallas.
Un nuevo generador de residuos es diseñado de manera que permite un desacoplo de las fallas con objeto de proporcionar funciones de ponderación robusta a fallas. Este nuevo generador de residuos da una primera señal insensible a las fallas, pero sensible a los errores de modelado y una segunda señal sensible a fallas. El nuevo generador de residuos se expresa como:

donde 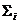 y
y 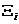 son términos
introducidos con el fin de desacoplar los residuos y tienen dimensiones
apropiadas;
son términos
introducidos con el fin de desacoplar los residuos y tienen dimensiones
apropiadas;  es el nuevo
vector de residuos. Esta consideración permite estudiar la detección de filtros
generando residuos desacoplados de fallas como [19], la cual nos proponen
generalizar en la estructura multi-modelo.
es el nuevo
vector de residuos. Esta consideración permite estudiar la detección de filtros
generando residuos desacoplados de fallas como [19], la cual nos proponen
generalizar en la estructura multi-modelo.
2.3 Función
de Ponderación Robusta
Bajo
la suposición de que ocurra una falla en el tiempo 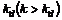 y que cambie el
punto de operación en el tiempo
y que cambie el
punto de operación en el tiempo  el vector de
residuo del i-ésimo filtro se expresa
como sigue [1]:
el vector de
residuo del i-ésimo filtro se expresa
como sigue [1]:
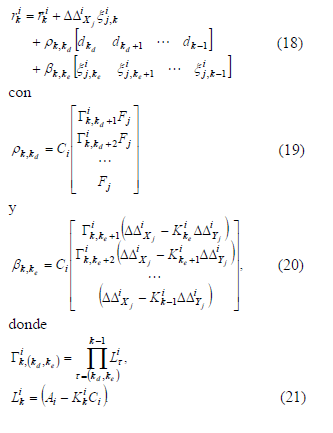
La ecuación (18) permite confirmar que el residuo es afectado por fallas y errores de modelado. El objetivo es generar residuos insensible a fallas pero sensible solo a errores de modelado, esto es,

Si la ecuación (22) se satisface y si el número de fallas es
estrictamente menor al número de salidas (i.e. 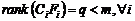 ), una solución a (22) fue propuesta en [19], el cual
parametriza una ganancia del filtro de Kalman como
), una solución a (22) fue propuesta en [19], el cual
parametriza una ganancia del filtro de Kalman como

con
 y
y 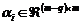 , es una matriz constante arbitraria definida, a fin
que la matriz
, es una matriz constante arbitraria definida, a fin
que la matriz  sea de rango de
fila completo. Por lo tanto, el residuo definido en (18) bajo las igualdades
(22) llega a ser
sea de rango de
fila completo. Por lo tanto, el residuo definido en (18) bajo las igualdades
(22) llega a ser
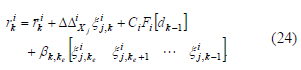
El filtro de Kalman también minimizaría la traza de la matriz de varianza-covarianza del error de estimación. Esta minimización se lleva a cabo bajo la existencia y condiciones de estabilidad presentada y estudiada en [19]. De acuerdo a la ecuación (23), cada filtro de detección, definida en la ecuación (8), se describe por
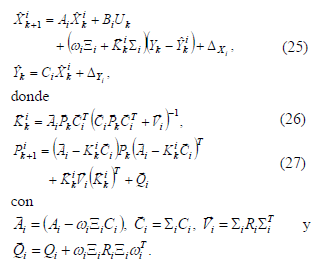
De acuerdo a (23) y las propiedades de las matrices previas, un vector
de residuos  se obtiene como
sugiere (17).
se obtiene como
sugiere (17).
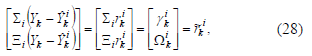
donde 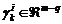 es el vector de
residuos desacoplado de fallas y
es el vector de
residuos desacoplado de fallas y  es el vector de
residuos sensible a fallas. Debido a las propiedades de las matrices
es el vector de
residuos sensible a fallas. Debido a las propiedades de las matrices 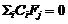 y
y 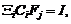 cada residuo de
(28) puede ser desarrollado de acuerdo a la ecuación (18) en vectores
cada residuo de
(28) puede ser desarrollado de acuerdo a la ecuación (18) en vectores 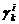 insensibles y
insensibles y 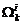 sensibles a
fallas, respectivamente. Como se expresa:
sensibles a
fallas, respectivamente. Como se expresa:
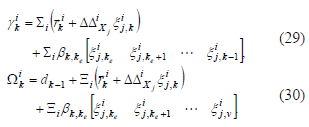
Las ecuaciones (29) y (30) indican que un banco de filtros de Kalman
desacoplados proporciona una solución al problema de distinción de fallas en un
enfoque multi-modelo. Con estas suposiciones, cuando el sistema opera alrededor
del j-ésimo punto de operación, el nuevo
residuo  insensible a
falla satisface las siguientes propiedades:
insensible a
falla satisface las siguientes propiedades:
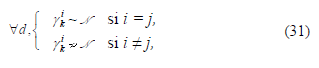
Considerando que el residuo 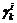 alrededor del j-ésimo punto de operación sigue una
distribución Gaussiana, el vector de residuos se usa para calcular la
distribución de probabilidad como
alrededor del j-ésimo punto de operación sigue una
distribución Gaussiana, el vector de residuos se usa para calcular la
distribución de probabilidad como

donde  define la
matriz de covarianza del residuo
define la
matriz de covarianza del residuo  igual a
igual a 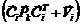 . La probabilidad robusta a falla se expresa como
. La probabilidad robusta a falla se expresa como

El algoritmo de probabilidad permite obtener un modelo global que describe
el comportamiento dinámico del sistema tanto en ausencia como en presencia de
fallas. Las probabilidades permiten determinar el punto de operación donde el
sistema está evolucionando. Estas probabilidades son usadas para aislar el
punto de operación y consecuentemente definir una función de activación
robusta. Nótese que cuando  , parece que las probabilidades no son iguales a uno o
cero pero pueden tomar algunos valores entre
, parece que las probabilidades no son iguales a uno o
cero pero pueden tomar algunos valores entre  y
y  Este caso
subraya el método de interpolación cuando el sistema está representado por
varios modelos definido alrededor de múltiples regímenes de operación. La
función de ponderación robusta
Este caso
subraya el método de interpolación cuando el sistema está representado por
varios modelos definido alrededor de múltiples regímenes de operación. La
función de ponderación robusta 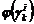 es usada para
representar el comportamiento dinámico de la planta como un conjunto convexo de
multi-modelos lineales tales que
es usada para
representar el comportamiento dinámico de la planta como un conjunto convexo de
multi-modelos lineales tales que

donde 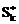 representa el
modelo global y
representa el
modelo global y 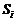 es definida
como
es definida
como
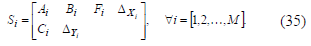
De acuerdo a (34), la representación del sistema en espacio de estado esta entonces definida como
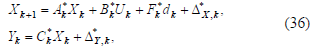
donde las matrices 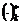 son igual a
son igual a  La ecuación
(36) representa una reestimación del sistema nominal sin suposiciones en estado
y mediciones de ruidos. Esta representación del conjunto convexo es usada para
diseñar un filtro adaptivo que se desarrollará en la siguiente sección para llevar
a cabo la detección, la localización y la estimación de las fallas.
La ecuación
(36) representa una reestimación del sistema nominal sin suposiciones en estado
y mediciones de ruidos. Esta representación del conjunto convexo es usada para
diseñar un filtro adaptivo que se desarrollará en la siguiente sección para llevar
a cabo la detección, la localización y la estimación de las fallas.
3. EJEMPLO DE SIMULACIÓN
El
método propuesto se aplica a un sistema no lineal discreto en lazo abierto que
se obtiene directamente de un ejemplo académico. Este sistema, consta de una
entrada y múltiples salidas. También está representado por un conjunto de tres
modelos lineales estocásticos discretos con las mismas dimensiones: 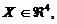
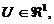 y
y 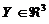 . El
. El  punto de
operación depende directamente de las magnitudes de las entradas definidas en
la tabla 1. Para simplificar la implementación,
punto de
operación depende directamente de las magnitudes de las entradas definidas en
la tabla 1. Para simplificar la implementación,
Tabla 1. Definición de puntos
de operación
Table 1. Operating points definition

otras matrices son las mismas para cada modelo: 

El sistema no lineal para el ejemplo académico queda definido en la ecuación (37) de la siguiente manera:

En
donde  y las otras
matrices se describen de igual manera.
y las otras
matrices se describen de igual manera.
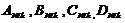 , así como
, así como 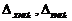 son matrices y
vectores de dimensiones apropiadas y variantes en el tiempo. Las matrices y
vectores
son matrices y
vectores de dimensiones apropiadas y variantes en el tiempo. Las matrices y
vectores 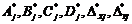 son también de
dimensiones apropiadas. Y están definidas con un escalar constante
son también de
dimensiones apropiadas. Y están definidas con un escalar constante  y una función
trigonométrica
y una función
trigonométrica  en donde
en donde 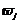 representa un
escalar constante. Las matrices en (37) están definidas a cada instante según
la dinámica del sistema no lineal
representa un
escalar constante. Las matrices en (37) están definidas a cada instante según
la dinámica del sistema no lineal 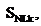 definida en (38)
por:
definida en (38)
por:
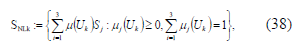
En
donde  es la función
de activación diseñada a través de tres intervalos en función de la entrada y
es la función
de activación diseñada a través de tres intervalos en función de la entrada y 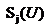 representa el
conjunto de matrices y vectores
representa el
conjunto de matrices y vectores 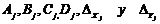 .
.
El
ejemplo de simulación considerado es desarrollado en caso de fallas múltiples
en los sensores 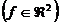 con una entrada
al sistema U elegida como pasos
sucesivos con transiciones suaves. En primer lugar, se propone un banco de tres
filtros de Kalman clásicos. Esto fue desarrollado para mostrar el problema que se
presento al inicio, con FDI y con la selección del modelo real, cuando el
vector de residuos es corrompido por dos piezas de información: la evolución
del punto de operación y la ocurrencia de la falla. En el mismo contexto, se
considera un banco de tres filtros de Kalman desacoplados como la solución a
los problemas presentados para la
FDI y la selección robusta del modelo, en un filtro de Kalman
clásico en una estructura MM. En este banco, cada filtro desacoplado es
diseñado de acuerdo con las consideraciones presentadas en la sección anterior.
La condición del rango
con una entrada
al sistema U elegida como pasos
sucesivos con transiciones suaves. En primer lugar, se propone un banco de tres
filtros de Kalman clásicos. Esto fue desarrollado para mostrar el problema que se
presento al inicio, con FDI y con la selección del modelo real, cuando el
vector de residuos es corrompido por dos piezas de información: la evolución
del punto de operación y la ocurrencia de la falla. En el mismo contexto, se
considera un banco de tres filtros de Kalman desacoplados como la solución a
los problemas presentados para la
FDI y la selección robusta del modelo, en un filtro de Kalman
clásico en una estructura MM. En este banco, cada filtro desacoplado es
diseñado de acuerdo con las consideraciones presentadas en la sección anterior.
La condición del rango 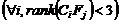 es así
satisfecha. Considerando estas condiciones, las fallas en los sensores pueden
ser detectadas, localizadas y estimadas. Para el diseño de los filtros
desacoplados con fallas en los sensores, un aumento en el espacio de estados
debe llevarse a cabo si se considera las fallas en los sensores como fallas en
los actuadores.
es así
satisfecha. Considerando estas condiciones, las fallas en los sensores pueden
ser detectadas, localizadas y estimadas. Para el diseño de los filtros
desacoplados con fallas en los sensores, un aumento en el espacio de estados
debe llevarse a cabo si se considera las fallas en los sensores como fallas en
los actuadores.
3.1 Resultados
de Simulación
Para
evaluar el método, consideramos que una falla aparece en el primer sensor en la
muestra  , con una magnitud constante igual a 2 y que una
segunda falla se presenta en el segundo sensor al instante de muestreo
, con una magnitud constante igual a 2 y que una
segunda falla se presenta en el segundo sensor al instante de muestreo 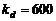 , con una magnitud constante igual a 5
, con una magnitud constante igual a 5 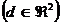 . Ambas fallas están definidas por la ecuación (3),
donde
. Ambas fallas están definidas por la ecuación (3),
donde 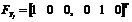 es la matriz de distribución de fallas. Los resultados
presentados aquí fueron logrados considerando un banco de filtros de Kalman clásicos.
es la matriz de distribución de fallas. Los resultados
presentados aquí fueron logrados considerando un banco de filtros de Kalman clásicos.
En la figura 1a, se muestra la entrada U del sistema. El comportamiento de la estimación de la función robusta del modelo, muestra su desempeño con respecto a la entrada del sistema como se ilustra en la figura 1b, en ausencia de fallas.

Figura 1. Entrada del sistema y evolución
del selector modelo en caso de ausencia de fallas
Figure 1. Input System and evolution of robust activation
function in fault free case
El vector de fallas y el vector de entrada al sistema se muestran en la
figura 2a. En la figura 2b, se puede observar que en presencia de fallas, la
función de ponderación no selecciona al modelo apropiado. La razón es que el
vector de residuos no es robusto a las fallas. Ahora, si se considera un filtro
de Kalman desacoplado, los parámetros de la matriz de ganancia 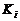 son
seleccionados con el propósito de construir un residuo desacoplado de fallas
con
son
seleccionados con el propósito de construir un residuo desacoplado de fallas
con  y
y  . Los resultados que se obtienen con el uso de un
banco de filtros de Kalman desacoplados, cuando dos fallas aparecen y está
cambiando el punto de operación se ilustra en la figura 3. El residuo
. Los resultados que se obtienen con el uso de un
banco de filtros de Kalman desacoplados, cuando dos fallas aparecen y está
cambiando el punto de operación se ilustra en la figura 3. El residuo  insensible a
las fallas para tres filtros, se gráfica en la figura 3a., en donde se observa
que de acuerdo a la entrada del sistema, el residuo correspondiente al modelo
verdadero tiene media cero. Así el residuo
insensible a
las fallas para tres filtros, se gráfica en la figura 3a., en donde se observa
que de acuerdo a la entrada del sistema, el residuo correspondiente al modelo
verdadero tiene media cero. Así el residuo  es usado para
mostrar la evolución del modo de probabilidad
es usado para
mostrar la evolución del modo de probabilidad  , como se ilustra en la figura 3b. Los resultados obtenidos
muestran una función de ponderación robusta la cual es insensible a las fallas. La
misma figura muestra la transición del modelo“ 1” al modelo“ 2” y después al
modelo“ 3”
sin que las probabilidades sean afectadas por la ocurrencia de fallas.
Finalmente, el vector global de residuos sensible a las fallas
, como se ilustra en la figura 3b. Los resultados obtenidos
muestran una función de ponderación robusta la cual es insensible a las fallas. La
misma figura muestra la transición del modelo“ 1” al modelo“ 2” y después al
modelo“ 3”
sin que las probabilidades sean afectadas por la ocurrencia de fallas.
Finalmente, el vector global de residuos sensible a las fallas 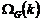 se ilustra en la figura 3c. Este se obtiene de los
vectores de residuos sensibles a las fallas
se ilustra en la figura 3c. Este se obtiene de los
vectores de residuos sensibles a las fallas  y usando el
modo de probabilidad tal como la ec.
y usando el
modo de probabilidad tal como la ec.  .
.
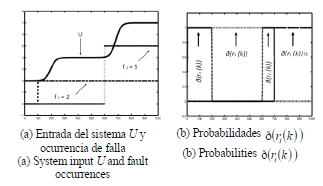
Figura 2. Entrada del sistema y evolución del modelo de selección en caso de
fallas
Figure 2. Input System and
and evolution of the robust activation function in faulty case

Figura 3. Comportamiento de residuos insensible a fallas, sensible a fallas y la
estimación de la función de ponderación robusta
Figure 3. Behaviors of the
residual insensitive to faults and the Estimation of the robust activation
function
En esta figura, se debe observar el comportamiento del residuo global de fallas, cuando hay cambios abruptos correspondientes a la aparición de dos fallas. Este resultado ilustrado en la figura 3c, hace posible la determinación de la detección y localización de las fallas. También se puede notar la exactitud de la estimación de ambas fallas. El enfoque sugerido en este estudio permite una detección, localización y estimación de ocurrencia de fallas, así como la estimación de la función de ponderación robusta que permite determinar la contribución del modelo lineal, en el marco de modelos múltiples.
4. CONCLUSIONES
En este artículo se presenta un método de diagnóstico de fallas en sistemas no lineales, el cual se encuentra representado por un conjunto finito de modelos lineales invariantes en el tiempo. Este método se basa en un banco de filtros de Kalman desacoplados, los cuales se diseñan para detectar, localizar y estimar la magnitud de múltiples fallas que se presentan de manera simultánea o secuencial. Las funciones de ponderación robustas a fallas fueron diseñadas para identificar la contribución de cada uno de los modelos lineales representativos del sistema no lineal en presencia y en ausencia de fallas, esto permite la construcción global del sistema estimado. La estimación de las funciones de ponderación está basada en vectores de residuos insensibles a las fallas, esto significa que las matrices de distribución de errores de modelado son completamente diferentes a las matrices de distribución de fallas. La ventaja del presente método es la fácil detección y localización de fallas a través de esquemas lineales pero resolviendo un sistema no lineal, gracias a la estrategia LIT multimodelos. Un ejemplo académico de simulación ilustra la funcionalidad del método propuesto sin mostrar aún toda la potencialidad del enfoque que se realiza.
REFERENCIAS
[1] ADAM-MEDINA, M., RODRIGUES, M., THEILLIOL, D., & JAMOULI, H. Fault diagnosis in nonlinear systems through an adaptive filter under a convex set representation. In Proceedings of the European control conference, Cambridge, UK , CD Rom. 2003.
[2] ALCORTA-GARCÍA, E., & FRANK, P. Deterministic nonlinear observer based approaches to fault diagnosis: A survey. Control Engineering Practice, 5(5), 663670. 1997.
[3] ATHANS, M., FEKRI, S., & PASCOAL, A. Issues on robust adaptive feedback control. In Proceedings of 16th IFAC world congress, Prague, Czech Republic . 2005.
[4] BANERJEE, A., ARKUN, Y., PEARSON, R., & OGUNNAIKE, B. H1control of nonlinear processes using multiple linear models. Proceedings of the European control conference, Roma, Italy . 26712676. 1995.
[5] BHAGWAT, A., SRINIVASAN, R., & KRISHNASWAMY, P. R. Multi-linear model-based fault detection during process transitions. Chemical Engineering Science, 58, 16491670. 2003.
[6] CHEN, J., & PATTON, R. Robust model-based fault diagnosis for dynamic systems. Dordrecht: Kluwer Academic Publishers. 1999.
[7] GATZKE, E., & DOYLE, F. Use of multiple models and qualitative knowledge for on-line moving horizon disturbance estimation and fault diagnosis. Journal of Process Control, 12, 339352. 2002.
[8] GERTLER, J. Fault detection and diagnosis in engineering systems. New York, Basel, Hong Kong: Marcel Dekker. 1998.
[9] MURRAY-SMITH, R., & JOHANSEN, T. Multiple model approaches to modelling and control. London: Taylor & Francis. 1997.
[10] NARENDRA, K., BALAKRISHNAN, J., & KERMAL, M. Adaptation and learning using multiple models, switching and tuning. IEEE Control Systems Magazine, 3751. 1995.
[11] DIAO, Y., & PASSINO, K. M. Intelligent fault-tolerant control using adaptive and learning methods. Control Engineering Practice, 10(8), 801817. 2002.
[12] PORFIRIO, C. R., NEITO, E. A., & ODLOAK, D. Multi-model predictive control of an industrial c3/c4 splitter. Control Engineering Practice, 11, 765779. 2003.
[13] RODRIGUES, M. Diagnostic et commande active tolerante aux defauts appliques aux systemes decrits par des multi-modeles lineaires. Ph.D. thesis, Centre de Recherche en Automatique de Nancy, UHP, Nancy, France. 2005.
[14] LEITH, D. J., & LEITHEAD, W. E. Survey of gain-scheduling analysis and design. International Journal of Control, 73(11), 10011025. 2000.
[15] WAN, Z., & KOTHARE, M. Efficient scheduled stabilizing model predictive control for constrained nonlinear systems. International Journal of Robust and Nonlinear Control, 13, 331346. 2003.
[16] TAYEBI, A., & ZAREMBA, M. Iterative learning control for nonlinear systems described by a blended multiple model representation. International Journal of Control, 75(16/17), 13761384. 2002.
[17] OZKAN, L., KOTHARE, M., & GEORGAKIS, C. Control of a solution copolymerization reactor using multi-model predictive control. Chemical Engineering Science, 2, 12071221. 2003.
[18] PARK, J., RIZZONI, G., & RIBBENS, W. On the representation of sensors faults in fault detection filters. Automatica, 30(11), 17931795. 1994.
[19] KELLER, J. Fault isolation filter design for linear stochastic systems. Automatica, 35, 17011706. 1999.
[20] ADAM, M. Diagnostic de Défauts de Systèmes a représentation Multi-Modèles Linéaires Invariants dans le Temps. Tesis de Doctorado, Universidad Nancy I, Francia. 2004.