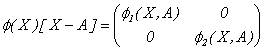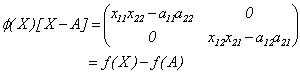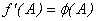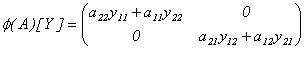CÁLCULO DE DERIVADAS EN ALGUNOS GRUPOS
TOPOLÓGICOS
CALCULUS
OF DERIVATIVES IN SOME TOPOLOGICAL GROUPS
HÉCTOR ANDRÉS
GRANADA
Matemático, Universidad Nacional de Colombia, Sede Manizales, hagranadad@unal.edu.co
SIMEÓN CASANOVA
TRUJILLO
Matemáticas, M.Sc, Profesor, Universidad Nacional de
Colombia, Sede Manizales, scasanovat@unal.edu.co
Recibido para revisar septiembre 10 de 2007, aceptado
Marzo 28 de 2008, versión final Julio 30 de 2008
RESUMEN: En este artículo se muestra a traves de ejemplos, la
forma como se calculan derivadas en grupos topológicos. En cada uno de ellos se
deben resolver ecuaciones diferenciales ordinarias o parciales.
PALABRAS
CLAVE: Grupo topológico, homomorfismo,
diferenciación en grupos topológicos.
ABSTRACT: This article shows how to calculate derivatives in topological groups
trough examples. In each of them one should solve ordinary or partial
differential equations.
KEYWORDS: Topological group,
homomorphism, differentiability in topological groups.
1. INTRODUCCIÓN
La
derivada de Carathéodory para funciones 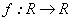 (
(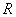 denota el conjunto de los números reales) le permitió a
Acosta y Delgado generalizar esta a
funciones
denota el conjunto de los números reales) le permitió a
Acosta y Delgado generalizar esta a
funciones  y mostrar su
equivalencia con la derivada de Fréchet [1]. Con base en este último trabajo, Acosta generalizó la derivada de
Carathéodory a grupos topológicos [2]. Tenemos así una forma de hacer cálculo diferencial
en grupos topológicos. Sin embargo, en [2] no se muestra explícitamente un
ejemplo en el que se calculen derivadas en grupos topológicos. En [3] se
y mostrar su
equivalencia con la derivada de Fréchet [1]. Con base en este último trabajo, Acosta generalizó la derivada de
Carathéodory a grupos topológicos [2]. Tenemos así una forma de hacer cálculo diferencial
en grupos topológicos. Sin embargo, en [2] no se muestra explícitamente un
ejemplo en el que se calculen derivadas en grupos topológicos. En [3] se
calculan
derivadas para una
función 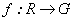 , donde
, donde 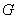 es un grupo que describiremos más adelante. En este artículo se
retomará el trabajo hecho en [3] y se calcularán derivadas para
funciones
es un grupo que describiremos más adelante. En este artículo se
retomará el trabajo hecho en [3] y se calcularán derivadas para
funciones  y
y  .
.
También se hará el
cálculo de derivadas para un tipo particular de funciones 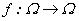 siendo
siendo 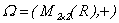 el grupo aditivo de
las matrices de tamaño
el grupo aditivo de
las matrices de tamaño  .
.
En general, el
cálculo de derivadas en grupos topológicos conduce a la solución de ecuaciones diferenciales.
2. PRELIMINARES
En
esta sección se presenta la definición de derivada en grupos topológicos dada
en [2]. Para llegar a ella, se hace necesario los siguientes comentarios:
1. El espacio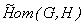 corresponde al conjunto de todos los homomorfismos continuos
de
corresponde al conjunto de todos los homomorfismos continuos
de 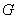 en
en 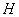 dotado de la topología compacto-abierta. Esta topología se
describe como sigue:
dotado de la topología compacto-abierta. Esta topología se
describe como sigue:
Sean 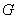 y
y 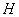 grupos topológicos Hausdorff. Si
grupos topológicos Hausdorff. Si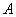 es un subconjunto compactode
es un subconjunto compactode 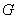 y
y 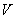 es un subconjunto abierto de
es un subconjunto abierto de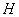 , se denota por
, se denota por 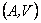 el conjuntode todas
las funciones continuas
el conjuntode todas
las funciones continuas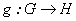 tales que
tales que  .
.
La
topología compacto-abierta es la que tiene como sub-base la colección 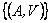 donde
donde 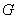 es localmente compacto.
es localmente compacto.
2. Un grupo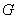 es divisible si para todo
es divisible si para todo 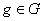 y
y  (
(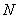 denota el conjunto
de los números naturales), la ecuación
denota el conjunto
de los números naturales), la ecuación 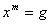 (en notación
multiplicativa) tiene solución.
(en notación
multiplicativa) tiene solución.
Definición 2.1. Sean 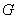 y
y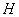 grupos topológicos Hausdorff. Una aplicación
grupos topológicos Hausdorff. Una aplicación 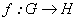 es diferenciable en
es diferenciable en 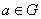 , si existe
, si existe  continua en
continua en  y tal que
y tal que
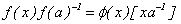
Si esta igualdad se
da y 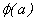 es única, la derivada de
es única, la derivada de 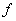 en
en  es
es 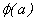 , y escribimos
, y escribimos 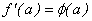 .
.
En la definición
anterior, la igualdad debe ser válida en alguna vecindad del punto  .
.
La operación del
lado derecho es una evaluación y la notación es tomada de [2], pues es allí
donde se da por primera vez una definición de derivada en grupos topológicos.
En [3] se dan
condiciones suficientes para la unicidad de la derivada:
Sean 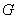 y
y 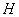 grupos topológicos Hausdorff,
grupos topológicos Hausdorff, 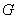 localmente compacto y
divisible. Supóngase además que para todo
localmente compacto y
divisible. Supóngase además que para todo 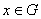 ,
,  . Si
. Si 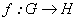 es diferenciable en
es diferenciable en 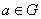 , entonces
, entonces 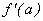 es única.
es única.
Se ve de la
definición de derivada, que 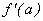 es un homomorfismo.
Por lo tanto, para hacer cálculo diferencial en grupos topológicos, se debe
empezar por calcular homomorfismos.
es un homomorfismo.
Por lo tanto, para hacer cálculo diferencial en grupos topológicos, se debe
empezar por calcular homomorfismos.
3. CÁLCULO DE HOMOMORFISMOS
En esta sección se hará el cálculo de ciertos
homomorfismos, para usarlos en la próxima sección con el fin de calcular
derivadas.
3.1 Consideremos el conjunto
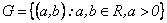
dotado de la ley de composición interna
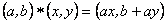
La dupla  es un grupo (no
abeliano), donde el módulo es la pareja ordenada
es un grupo (no
abeliano), donde el módulo es la pareja ordenada  y el
y el
inverso de  es
es 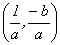 . Si se considera en
. Si se considera en 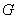 la topología
inducida por la usual U de
la topología
inducida por la usual U de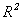 , se tiene que la tripla
, se tiene que la tripla 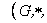 U
U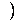 es un grupo topológico.
es un grupo topológico.
3.1.1 Homomorfismos de G en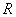
Sea 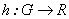 un homomorfismo.
Entonces,
un homomorfismo.
Entonces,
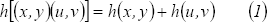
Se
tiene además la condición inicial
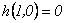 .
.
Como 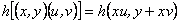
entonces
de 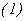 obtenemos que
obtenemos que
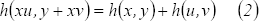
Haciendo 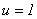 ,
, 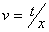 y usando la
condición inicial en
y usando la
condición inicial en 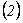 , se llega a:
, se llega a:

Tomando el límite cuando 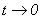 se
tiene:
se
tiene:
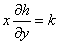
de donde
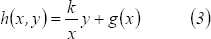
Derivando en esta última igualdad respecto a la variable 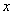 se obtiene:
se obtiene:
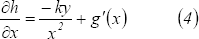
Ahora, en (2) se hace  y obtenemos
y obtenemos

Tomando el límite cuando 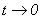 obtenemos:
obtenemos:

De  y
y  se llega a:
se llega a:

Para que esta última igualdad sea válida debe ser que 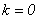 , de donde
, de donde
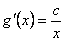
Así, 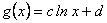 y en particular
y en particular 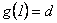 . De
. De  se tiene que
se tiene que

Luego, 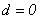 , o sea que
, o sea que  . Remplazando en
. Remplazando en  se llega a que los
homomorfismos
se llega a que los
homomorfismos 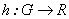 quedan caracterizados
como:
quedan caracterizados
como:

3.1.2 Homomorfismos de 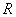 en G.
en G.
Sea  un homomorfismo. En
primer lugar,
un homomorfismo. En
primer lugar,
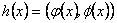 .
.
Ahora, como 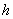 es homomorfismo entonces
es homomorfismo entonces
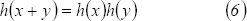
Por un lado se tiene que
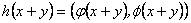
y por otro lado

Remplazando las dos
últimas relaciones en (6), se obtienen las siguientes
relaciones funcionales:
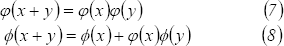
Como  se tienen además las condiciones
iniciales
se tienen además las condiciones
iniciales .
.
De (7) y las condiciones
iniciales obtenemos
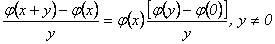
Tomando el límite
cuando 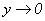 se llega a que
se llega a que  , de donde
, de donde 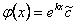 . De esta igualdad se sigue que
. De esta igualdad se sigue que 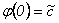 y usando las condiciones iniciales se tiene que
y usando las condiciones iniciales se tiene que 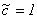 , así que
, así que

Ahora, de 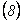 y
y  junto con las condiciones iniciales, se tiene que:
junto con las condiciones iniciales, se tiene que:
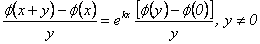
Tomando el límite
cuando 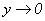 se obtiene
se obtiene 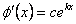 , de donde
, de donde  . De esta igualdad se sigue que
. De esta igualdad se sigue que 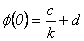 y usando las
condiciones iniciales se llega a que
y usando las
condiciones iniciales se llega a que 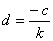 . Por lo tanto,
. Por lo tanto,

De (9) y (10) concluimos que los
homomorfismos  quedan caracterizados
como:
quedan caracterizados
como:
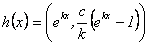
3.1.3 Homomorfismos de G en G. Sea 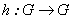
Un homomorfismo. En
primer lugar,
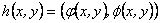
Como 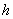 es homomorfismo, entonces
es homomorfismo, entonces
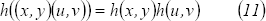
Por un lado

y por otro lado
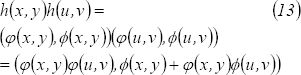
Remplazando  y
y 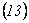 en
en  se obtienen las
siguientes relaciones funcionales:
se obtienen las
siguientes relaciones funcionales:

También, como 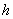 es homomorfismo se sigue que
es homomorfismo se sigue que  , de donde se tienen las condiciones iniciales
, de donde se tienen las condiciones iniciales
 .
.
En (14) se hace 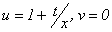 y se obtiene
y se obtiene
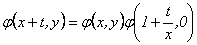
Usando las condiciones iniciales, se llega a:
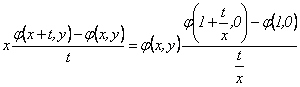
Tomando el límite
cuando 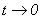 en esta última
igualdad obtenemos la ecuación diferencial parcial
en esta última
igualdad obtenemos la ecuación diferencial parcial

de donde
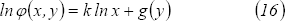
En esta igualdad
derivamos respecto a  y se tiene:
y se tiene:
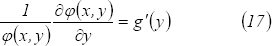
Usando nuevamente la
relación  , hacemos
, hacemos  y se obtiene:
y se obtiene:

Tomando el límite
cuando 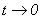 en esta última
igualdad se llega a:
en esta última
igualdad se llega a:

de donde
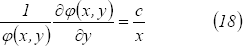
De  y
y  se tiene que
se tiene que 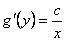 y para que esta
igualdad tenga sentido, debe ser que
y para que esta
igualdad tenga sentido, debe ser que  y de ahí que
y de ahí que 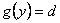 . Ahora, de
. Ahora, de  se tiene que
se tiene que
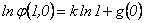
de donde 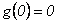 .
Luego,
.
Luego, 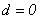 ,
es decir,
,
es decir, 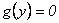 . De esta forma, de
. De esta forma, de  se sigue que
se sigue que

Para encontrar la
función  , en
, en 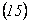 se hace
se hace 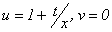 y razonando como antes
se obtiene
y razonando como antes
se obtiene

En conclusión, de  y
y  se tiene que los
homomorfismos
se tiene que los
homomorfismos 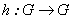 quedan
caracterizados como:
quedan
caracterizados como:
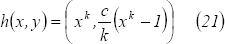
Se observa en los
ejemplos que los homomorfismos encontrados dependen únicamente de la primera
variable.
También en este
ejemplo, se tiene que los homomorfismos de 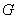 en
en 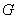 se obtienen realizando
la composición de los homomorfismos de
se obtienen realizando
la composición de los homomorfismos de 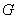 en
en 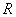 con los de
con los de 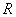 en
en 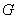 .
.
4. CÁLCULO DE DERIVADAS
4.1 Una vez hecho el cálculo de los homomorfismos 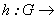
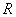 ,
, 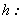
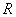
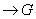 y
y 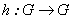 pasamos a calcular derivadas. El grupo
pasamos a calcular derivadas. El grupo 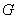 es localmente compacto
y satisface las condiciones para que haya unicidad de la derivada (comentario 3
de los preliminares).
es localmente compacto
y satisface las condiciones para que haya unicidad de la derivada (comentario 3
de los preliminares).
4.1.1 Derivada para funciones 
Veamos en primer
lugar qué funciones  son
diferenciables. Por la caracterización de los homomorfismos
son
diferenciables. Por la caracterización de los homomorfismos 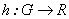 se tiene:
se tiene:

Haciendo  en esta igualdad se
obtiene:
en esta igualdad se
obtiene:

Como  debe ser continua en
debe ser continua en  se tiene entonces que
se tiene entonces que

Se exige entonces
que exista la derivada parcial de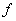 con respecto a
con respecto a 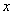 , evaluada en
, evaluada en  .
.
De esta manera, la
derivada de 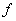 en
en  , evaluada en
, evaluada en  es :
es :

4.1.2 Derivada para funciones 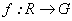
En primer lugar se
debe ver qué funciones 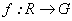 son
diferenciables, es decir, para qué funciones
son
diferenciables, es decir, para qué funciones 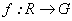 existe
existe  continua en
continua en  y tal que
y tal que

Tenemos que  , siendo
, siendo  y
y 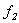 funciones de
funciones de 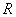 en
en 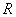 con
con  . Por un lado se tiene que
. Por un lado se tiene que
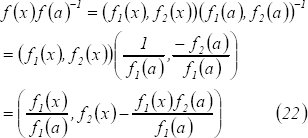
Por otra parte,
teniendo en cuenta la caracterización de los homomorfismos de 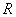 en
en 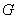 , tenemos:
, tenemos:
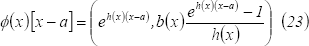
De (22) y (23) se obtienen las siguientes relaciones:
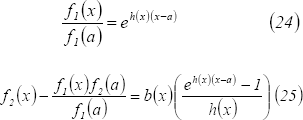
Al despejar  en
en  se llega a:
se llega a:

Como 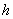 debe ser continua
debe ser continua  , entonces
, entonces

Se debe exigir
entonces que 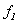 sea diferenciable en
sea diferenciable en  .
.
Ahora, de la
ecuación  se tiene:
se tiene:
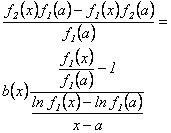
o bien,
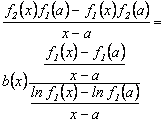
es decir,

Como  debe ser continua en
debe ser continua en  , entonces si en la anterior igualdad se toma el límite
cuando
, entonces si en la anterior igualdad se toma el límite
cuando  se tiene que:
se tiene que:

Se debe exigir
entonces que 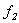 sea diferenciable en
sea diferenciable en  .
.
De (26) y (27) se tiene que la
derivada de 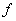 en
en  , evaluada en
, evaluada en  es:
es:
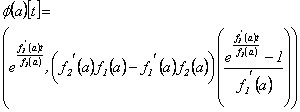
4.1.3 Derivada para funciones 
Como antes, veamos
qué funciones 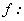
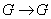 son diferenciables.
Tenemos que
son diferenciables.
Tenemos que
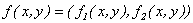
y por lo tanto,
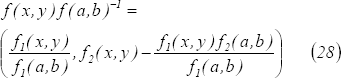
De otro lado,
teniendo en cuenta la caracterización de los homomorfismos de 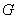 en
en 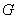 , se tiene que
, se tiene que
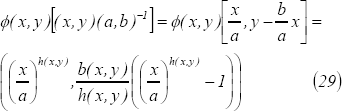
Igualando  y
y  se obtienen las
siguientes ecuaciones:
se obtienen las
siguientes ecuaciones:
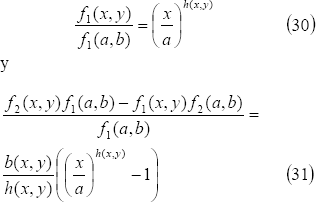
De  se llega a:
se llega a:
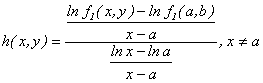
Haciendo  y teniendo en cuenta
que
y teniendo en cuenta
que 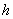 debe ser continua en
debe ser continua en  , entonces al tomar
, entonces al tomar  en la última igualdad, se obtiene que
en la última igualdad, se obtiene que
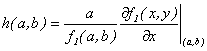
Ahora, de  se sigue que:
se sigue que:
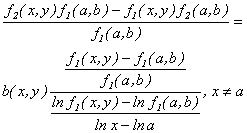
o bien,

Como  debe ser continua en
debe ser continua en  , entonces haciendo
, entonces haciendo  y tomando
y tomando  en la última igualdad,
se tiene que:
en la última igualdad,
se tiene que:
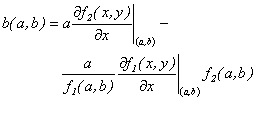
De esta manera, la
derivada de 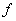 en
en  , evaluada en
, evaluada en 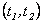 es
es
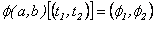
Donde 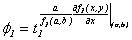 y
y
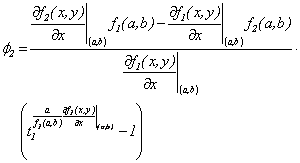
4.2 En esta sección se considerará
el grupo topológico aditivo 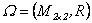 de las matrices
cuadradas de tamaño
de las matrices
cuadradas de tamaño 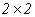 con entradas reales, el cual es localmente
compacto, divisible y satisface las condiciones para la unicidad de derivada. En efecto, la divisibilidad se sigue del
siguiente hecho: como estamos considerando
con entradas reales, el cual es localmente
compacto, divisible y satisface las condiciones para la unicidad de derivada. En efecto, la divisibilidad se sigue del
siguiente hecho: como estamos considerando 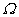 como grupo aditivo la
divisibilidad significa que dado
como grupo aditivo la
divisibilidad significa que dado 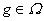 y
y  natural, existe
natural, existe 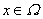 tal que
tal que  , lo cual en nuestro caso se tiene. Vale además que
, lo cual en nuestro caso se tiene. Vale además que  para todo
para todo 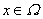 . La compacidad local de
. La compacidad local de 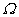 se sigue al ver
se sigue al ver 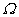 como
como  .
.
Definimos 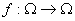 como:
como:
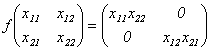
Se mostrará que esta
función es diferenciable en cada 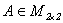 . En [4] se demuestra que los homomorfismos de
. En [4] se demuestra que los homomorfismos de 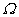 en
en 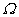 quedan caracterizados
como:
quedan caracterizados
como:
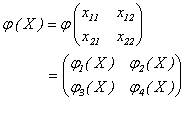
Donde
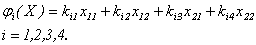
Debido a la
linealidad de las 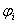 , se tiene que el homomorfismo
, se tiene que el homomorfismo 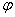 es continuo con la
topología inducida por la de
es continuo con la
topología inducida por la de  .
.
Definamos  como:
como:
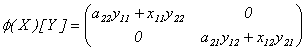
Con relación a esta
definición, tenemos que efectivamente 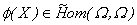 y que considerando en
y que considerando en  la topología compacto abierta, la aplicación
la topología compacto abierta, la aplicación  es continua en
es continua en 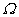 . Además,
. Además,
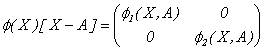
Donde

Se tiene así que
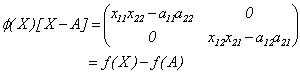
Por lo tanto, 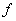 es diferenciable en
es diferenciable en 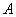 y
y
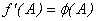
Donde
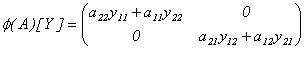
5. AGRADECIMIENTOS
Los autores expresan sus agradecimientos a los jurados del
artículo por sus acertados comentarios, los cuales permitieron mejorar su
presentación.
REFERENCIAS
[1] ACOSTA G. ERNESTO, DELGADO CÉSAR. Fréchet vs. Carathédory. American Mathematical Monthly, April 1994.
[2] ACOSTA G. ERNESTO. Differentiability in Topological Groups. Soochow Journal of Mathematics, Volume 22, No.1, pp 39-48. January 1996.
[3] CASANOVA T. SIMEÓN. Teorema del Valor Medio en Grupos Topológicos. Tesis de Maestría en Matemáticas. U.Nal. de Colombia, 1997.
[4] GRANADA D. HÉCTOR. Diferenciación en grupos metrizables. Tesis de grado en Matemáticas. U.Nal. de Colombia, Sede Manizales. Marzo de 2005.
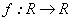 (
(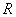 denota el conjunto de los números reales) le permitió a
Acosta y Delgado generalizar esta a
funciones
denota el conjunto de los números reales) le permitió a
Acosta y Delgado generalizar esta a
funciones  y mostrar su
equivalencia con la derivada de Fréchet [1]. Con base en este último trabajo, Acosta generalizó la derivada de
Carathéodory a grupos topológicos [2]. Tenemos así una forma de hacer cálculo diferencial
en grupos topológicos. Sin embargo, en [2] no se muestra explícitamente un
ejemplo en el que se calculen derivadas en grupos topológicos. En [3] se
y mostrar su
equivalencia con la derivada de Fréchet [1]. Con base en este último trabajo, Acosta generalizó la derivada de
Carathéodory a grupos topológicos [2]. Tenemos así una forma de hacer cálculo diferencial
en grupos topológicos. Sin embargo, en [2] no se muestra explícitamente un
ejemplo en el que se calculen derivadas en grupos topológicos. En [3] se 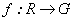 , donde
, donde 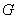 es un grupo que describiremos más adelante. En este artículo se
retomará el trabajo hecho en [3] y se calcularán derivadas para
funciones
es un grupo que describiremos más adelante. En este artículo se
retomará el trabajo hecho en [3] y se calcularán derivadas para
funciones  y
y  .
. 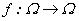 siendo
siendo 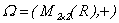 el grupo aditivo de
las matrices de tamaño
el grupo aditivo de
las matrices de tamaño  .
.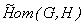 corresponde al conjunto de todos los homomorfismos continuos
de
corresponde al conjunto de todos los homomorfismos continuos
de 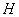 dotado de la topología compacto-abierta. Esta topología se
describe como sigue:
dotado de la topología compacto-abierta. Esta topología se
describe como sigue: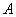 es un subconjunto compactode
es un subconjunto compactode 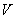 es un subconjunto abierto de
es un subconjunto abierto de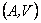 el conjuntode todas
las funciones continuas
el conjuntode todas
las funciones continuas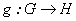 tales que
tales que  .
.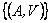 donde
donde 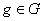 y
y  (
(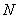 denota el conjunto
de los números naturales), la ecuación
denota el conjunto
de los números naturales), la ecuación 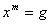 (en notación
multiplicativa) tiene solución.
(en notación
multiplicativa) tiene solución.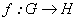 es diferenciable en
es diferenciable en 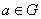 , si existe
, si existe  continua en
continua en  y tal que
y tal que 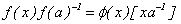
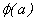 es única, la derivada de
es única, la derivada de 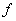 en
en 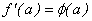 .
. 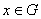 ,
,  . Si
. Si 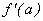 es única.
es única.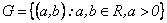
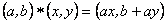
 es un grupo (no
abeliano), donde el módulo es la pareja ordenada
es un grupo (no
abeliano), donde el módulo es la pareja ordenada  y el
y el  es
es 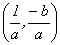 . Si se considera en
. Si se considera en 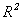 , se tiene que la tripla
, se tiene que la tripla 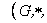 U
U es un grupo topológico.
es un grupo topológico. 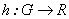 un homomorfismo.
Entonces,
un homomorfismo.
Entonces, 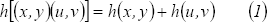
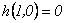 .
.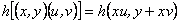
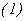 obtenemos que
obtenemos que 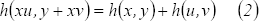
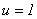 ,
, 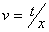 y usando la
condición inicial en
y usando la
condición inicial en 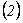 , se llega a:
, se llega a:
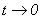 se
tiene:
se
tiene: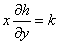
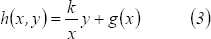
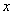 se obtiene:
se obtiene: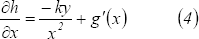
 y obtenemos
y obtenemos

 y
y  se llega a:
se llega a:
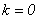 , de donde
, de donde 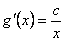
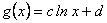 y en particular
y en particular 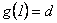 . De
. De  se tiene que
se tiene que 
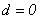 , o sea que
, o sea que  . Remplazando en
. Remplazando en 
 un homomorfismo. En
primer lugar,
un homomorfismo. En
primer lugar, 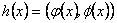 .
.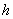 es homomorfismo entonces
es homomorfismo entonces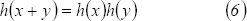
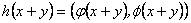

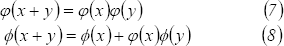
 se tienen además las condiciones
iniciales
se tienen además las condiciones
iniciales .
.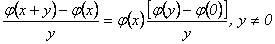
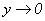 se llega a que
se llega a que  , de donde
, de donde 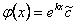 . De esta igualdad se sigue que
. De esta igualdad se sigue que 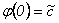 y usando las condiciones iniciales se tiene que
y usando las condiciones iniciales se tiene que 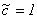 , así que
, así que 
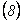 y
y  junto con las condiciones iniciales, se tiene que:
junto con las condiciones iniciales, se tiene que: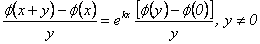
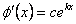 , de donde
, de donde  . De esta igualdad se sigue que
. De esta igualdad se sigue que 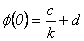 y usando las
condiciones iniciales se llega a que
y usando las
condiciones iniciales se llega a que 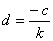 . Por lo tanto,
. Por lo tanto, 
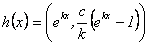
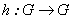
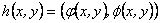
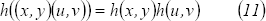

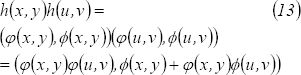
 y
y 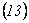 en
en  se obtienen las
siguientes relaciones funcionales:
se obtienen las
siguientes relaciones funcionales:
 , de donde se tienen las condiciones iniciales
, de donde se tienen las condiciones iniciales  .
.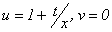 y se obtiene
y se obtiene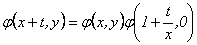
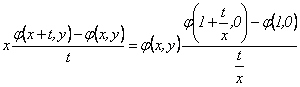

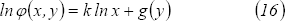
 y se tiene:
y se tiene: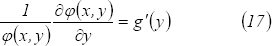
 , hacemos
, hacemos  y se obtiene:
y se obtiene:

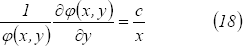
 y
y  se tiene que
se tiene que 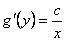 y para que esta
igualdad tenga sentido, debe ser que
y para que esta
igualdad tenga sentido, debe ser que  y de ahí que
y de ahí que 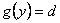 . Ahora, de
. Ahora, de  se tiene que
se tiene que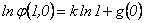
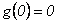 .
Luego,
.
Luego, 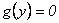 . De esta forma, de
. De esta forma, de  se sigue que
se sigue que
 , en
, en 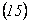 se hace
se hace 
 y
y  se tiene que los
homomorfismos
se tiene que los
homomorfismos 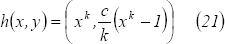
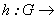
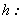
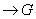 y
y 
 en esta igualdad se
obtiene:
en esta igualdad se
obtiene: 
 debe ser continua en
debe ser continua en  se tiene entonces que
se tiene entonces que
 es :
es :
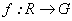
 continua en
continua en 
 , siendo
, siendo  y
y 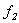 funciones de
funciones de  . Por un lado se tiene que
. Por un lado se tiene que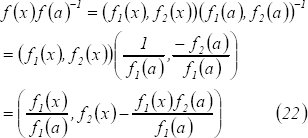
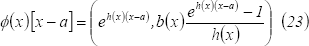
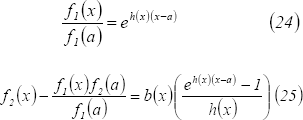
 en
en  se llega a:
se llega a:

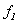 sea diferenciable en
sea diferenciable en  se tiene:
se tiene: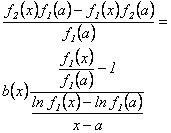
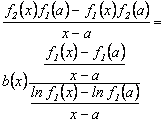

 se tiene que:
se tiene que:
 es:
es: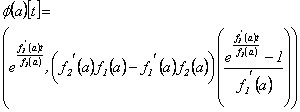
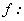
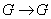 son diferenciables.
Tenemos que
son diferenciables.
Tenemos que 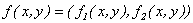
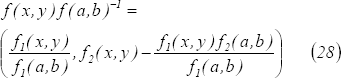
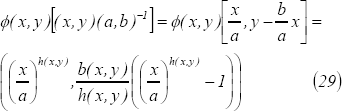
 y
y  se obtienen las
siguientes ecuaciones:
se obtienen las
siguientes ecuaciones: 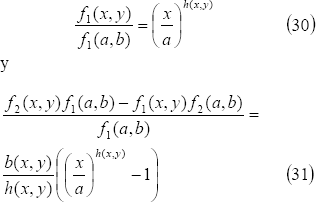
 se llega a:
se llega a: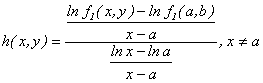
 y teniendo en cuenta
que
y teniendo en cuenta
que 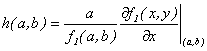
 se sigue que:
se sigue que: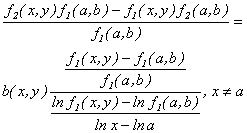

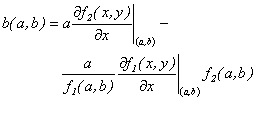
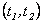 es
es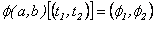
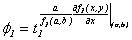 y
y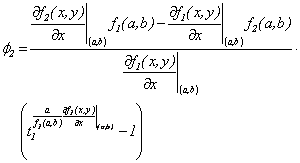
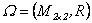 de las matrices
cuadradas de tamaño
de las matrices
cuadradas de tamaño 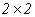 con entradas reales, el cual es localmente
compacto, divisible y satisface las condiciones para la unicidad de derivada. En efecto, la divisibilidad se sigue del
siguiente hecho: como estamos considerando
con entradas reales, el cual es localmente
compacto, divisible y satisface las condiciones para la unicidad de derivada. En efecto, la divisibilidad se sigue del
siguiente hecho: como estamos considerando 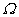 como grupo aditivo la
divisibilidad significa que dado
como grupo aditivo la
divisibilidad significa que dado 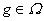 y
y  natural, existe
natural, existe 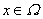 tal que
tal que  , lo cual en nuestro caso se tiene. Vale además que
, lo cual en nuestro caso se tiene. Vale además que  para todo
para todo  .
.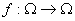 como:
como: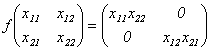
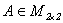 . En [4] se demuestra que los homomorfismos de
. En [4] se demuestra que los homomorfismos de 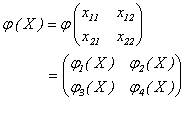
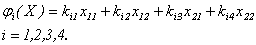
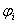 , se tiene que el homomorfismo
, se tiene que el homomorfismo 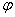 es continuo con la
topología inducida por la de
es continuo con la
topología inducida por la de  como:
como: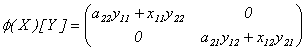
 y que considerando en
y que considerando en  la topología compacto abierta, la aplicación
la topología compacto abierta, la aplicación