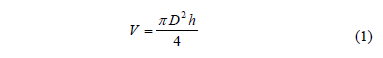
https://doi.org/10.15446/dyna.v81n188.41321
Influence of osmotic pre-treatment on convective drying of yellow pitahaya
Influencia de un pre-tratamiento osmótico sobre el secado convectivo de pitahaya amarilla
Alfredo Ayala-Aponte a, Liliana Serna-Cock b, Jimena Libreros-Triana a, Claudia Prieto a & Karina Di Scala c,d
a School of Food Engineering. Universidad del Valle.
Cali. Colombia, alfredo.ayala@correounivalle.edu.co
b Facultad de Ingeniería y Administración. Universidad Nacional de
Colombia, Palmira. Colombia, lserna@unal.edu.co
c Food Engineering Research Group. Universidad Nacional de
Mar del Plata, Buenos Aires, Argentina, kdiscala@gmail.com
d CONICET - Consejo Nacional de Investigaciones Científicas y Técnicas, Buenos
Aires, Argentina.
Received: December 23th, 2013. Received in revised form: September 19th, 2014. Accepted: November 6th, 2014.
Abstract
Cylinders of pitahayas were osmotically dehydrated in
sucrose 55 % (w/w) during 45 minutes as a pretreatment of convective drying.
Hot air drying was performed at 50, 60 and 70°C. Drying kinetics of osmodehydrated samples
was compared to untreated samples. Effective moisture diffusion coefficients
were determined. Values of activation energy were 29.56 and 16.93 kJ mol-1 for pretreated samples and untreated samples, respectively. Mathematical
modeling was applied to simulate the experimental drying curves of pitahayas.
Results indicated that the Weibull model could be used to simulate experimental
drying data. Furthermore, shrinkage of samples due to changes in volume was
more pronounced for fruits dehydrated without pretreatment.
Keywords: drying kinetics; effective diffusion coefficient; mathematical modelling; shrinkage; pitahayas.
Resumen
Cilindros de
pitahayas fueron osmóticamente deshidratados en sacarosa 55 % (p/p) durante 45
minutos como un pre-tratamiento al secado convectivo. El secado por aire
caliente se realizó a 50, 60 y 70°C. Se comparó la cinética de secado de las
muestras osmodeshidratadas con las muestras no tratadas. Se determinaron los
coeficientes de difusión efectiva. Los valores de la energía de activación
fueron 29.56 y 16.93 kJ mol-1 para las muestras pre-tratadas y para
las no tratadas, respectivamente. Se aplicó modelado matemático para simular
las curvas experimentales de secado de las pitahayas. Los resultados indicaron
que el modelo de Weibull podría ser usado para simular los datos de secado
experimental. Además, el encogimiento de las muestras debido a cambios en el
volumen fue más pronunciado en las muestras sin pretratar.
Palabras clave: cinética de secado; coeficiente efectivo de difusión; modelado matemático; encogimiento; pitahayas.
1. Introduction
Yellow pitahaya (Selenicereus megalanthus) is a tropical plant native to Central and South America which belongs to the Cactaceae family. Its fruits have yellow skin and a sweet and aromatic white flesh with small black seeds [1]. Growing exports in Colombia are driven by high demand in Europe and the Middle East. Moreover, this pitahaya is a polyphenol-rich fruit and a good source of antioxidants components, like phenolic compounds and ascorbic acid. Therefore, its consumption may be associated with nutraceutical properties due to its antioxidant capacity generated by their effect on free radicals, reducing the risk of chronic diseases [2]. In addition, pitahaya is a source of glucose, fructose, dietary fiber, vitamins, and minerals [3,4].
Because of its high water content, pitahaya is susceptible to deterioration, thus stabilization of the fruits requires reducing the moisture content up to certain level, at which microbial spoilage and chemical reactions deterioration are greatly minimised is desirable for its preservation [5].
Conventional air-drying is a simultaneous heat and mass transfer process and it is a high cost process. Moreover, it brings about substantial reduction in weight and volume, minimising packing, storage and transportation costs and enabling storability of the product under ambient temperatures [6]. However, during drying foods undergo physical, structural, chemical and nutritional changes that cause quality degradation [7].
In recent years, osmotic dehydration (OD) has received increasing attention in the field of fruit preservation in order to reduce energy consumption and improve quality of fruit product [8,9]. Moreover, the effects of osmotic pre-treatment on drying rates have been investigated by several authors and vary according to the raw material used and the drying conditions [10,11]. Sucrose is considered one of the best osmotic substances, especially when the OD is employed before drying. Dehydrated fruits have a rapid growing market due to consumer's demands for high quality dry products [9].
In order to control and optimize the drying process, it is necessary to use mathematical equations to simulate water transport phenomena. Therefore, the purpose of this work was to evaluate the drying kinetics of pitahaya subjected to osmotic dehydration in sucrose solution and to compare with the drying kinetics of untreated fruits. Simulation of drying kinetics by means of mathematical models was evaluated. Moreover, effective diffusion coefficients were determined and the effects of drying temperature on kinetics parameters as well as on samples collapse were also studied.
2. Materials and methods
2.1. Preparation of raw material
Yellow pitahayas (Selenicereus megalanthus) from the Department of Valle del Cauca, Colombia were used. Fruits were harvested at maturity state level four according to classification of Norma Técnica Colombiana (NTC) 3554 [12]. The fruits were washed with chlorinated water (200 ml/l) and peeled with stainless steel knifes. Then, they were cut into cylinders of 3 mm of length and 30 mm of diameter using a cutter machine (SKYMSEN, Poli, Brusque, Brasil) using a cylindrical stainless steel a cork borer.
2.2. Physico-chemical analysis
The moisture content was determined by direct heating in a drying oven at 105 °C for 48 h according to the AOAC method 931.04 [13]. Soluble solids (°Brix) were measured using a refractometer (ABBE, 1T, Tokio, Japan). The water activity was measured with a aw-meter (Aqualab, Serie 4TE, Pullman,WA, US) with an accuracy of ± 0.003. The sample volume (V) was determined using the Eq. (1). A caliper was used for measuring heights (h) and diameters (D). All measurements were done in triplicate.
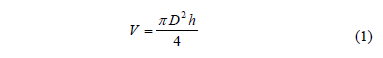
Shrinkage of pitahaya during dehydration can be correlated with the dimensionless moisture content (Xwt/Xw0), by means of empirical polynomial equations according to the work of Mayor & Sereno, 2004 [14]:
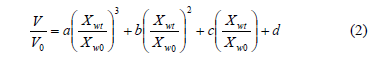
2.3. Osmotic dehydration
The cylinders of pitahaya were immersed in the osmotic solution of sucrose 55 % (w/w) at 27± 0.2°C during 45 minutes. These osmotic treatment conditions were selected according to a prior study on kinetics of osmotic dehydration of yellow pitahaya fruit [15]. Experiments were performed with a constant magnetic agitation of 500 rpm with an agitation equipment (Kika Labor Technik Pol Co, US). The solution was agitated continuously with a magnetic stirrer to maintain a uniform temperature throughout the experiment, thus, enhancing equilibrium conditions. The weight ratio of osmotic solution to pitahaya was 15:1 to maintain a constant concentration of the osmotic solution during OD. After 45 minutes, the samples were removed from the solution, drained, and blotted with absorbent paper to remove the excess solution.
2.4. Convective dehydration
The non-treated as well as the pretreated samples (dehydrated by osmotic dehydration) were put in a convective lab dryer (Armfield, UOP8, US) at three different air drying temperatures (50, 60 and 70°C) employing a constant air flow of 0.77 m/s (perpendicular direction to samples). This dryer consists in a tunnel with an air flower. Samples were measured during drying at 10, 20, 30, 40, 50, 60, 80, 100, 130, 160, 190, 230, 270, 320, 370 and 420 min by means of an electronic balance (Ohaus, Adventurer, NJ,US) with an accuracy of ±0.01 g. Initial and final moisture content of samples were determined according to AOAC (1990).
2.5. Estimation of water diffusion coefficient
Fick's second diffusion law has been widely used to describe drying kinetics and osmotic drying kinetics for biological materials [7, 16]. In this model, the dependent variable is the moisture ratio (MR) which relates the sample moisture content in real time to initial moisture contents Eq. (3). In this study, equilibrium moisture was assumed to be negligible. When internal mass transfer is the controlling mechanism and unidimensional transport in a slab or a cylinder with constant effective diffusivity can be assumed, the solution of the Fick's second law is given by Eq. (4) and Eq. (6). For sufficiently long drying times, the first term in the series expansion gives a good estimate of the solutions, Eq. (5) and Eq. (7) [17]. Based on Eqs. (4) and (6) and applying Newman's rule for a finite cylinder (Eq.(8)), a relationship between logarithm of dimensionless moisture content for plate and cylinder and time is obtained, which can be used to determine water diffusion coefficient (Dwe).
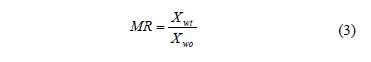
For an infinite slab:
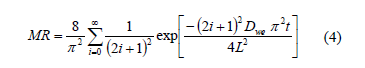
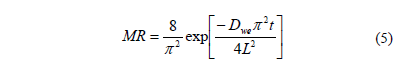
For an infinite cylinder:
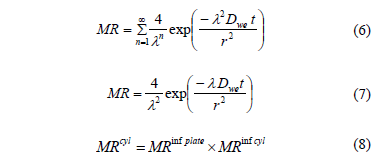
Where Xwt is the moisture content (g water g-1 dry matter), Xwo is the initial moisture content (g water g-1 dry matter), Dwe is the diffusion coefficient (m2 s-1), t is the drying time (s), L is the half-thickness of the slab (m), r is de radius of the cylinder and l=2.405 is the root of Bessel function for n=1.
2.6. Modelling of drying kinetics
Numerous mathematical models have been proposed to describe the characteristics of agricultural products during drying [6]. In this research, four of the more known models were used to fit the drying experimental data, including Newton (Eq 9), Henderson-Pabis (Eq. 10), Peleg (Eq. 11) and standardized Weibull model (Eq. 12). Applications of mentioned models can be found in different previous works [18,19]:
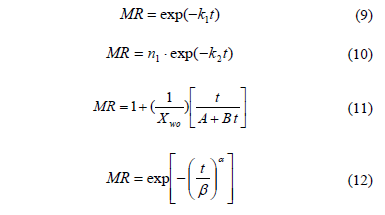
Where ki is the kinetic parameters (min-1), ni (i = 1…3) are the empirical parameters (dimensionless), a is the shape parameter (dimensionless) and b is the scale parameter (min) of the Weibull model, t is the drying time (min) and i is the number of terms.
In order to determine the influence of the process temperature on the diffusion coefficient (Dwe) and kinetics parameters, an Arrhenius-type equation was applied (Eq. 13).
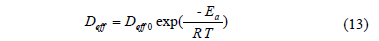
Where R is the universal gas constant (8.314 J K-1 mol-1) and T is the absolute temperature (K). Eq. (13) can be linearized by applying natural log at both sides and a plot of ln Y versus 1/T produce a straight line, from which the activation energy (Ea, kJ mol-1) can be determined [20].
2.7. Statistical evaluation of the models
Fit quality of the proposed models for simulating the drying kinetics data was evaluated by means of statistical tests including determination correlation coefficient (r2) [Eq. (14)] and sum squared errors (SSE) [Eq. (15)].
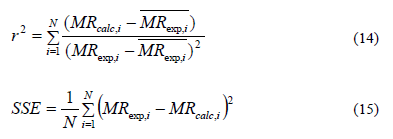
Where N is the number of data values and z is the number of constants.
Coefficients of Eq.. (2) were estimated by means of mathematical routines applying the function "lsqcurvefit" of the program Matlab 7.7.
3. Results and discussion
3.1. Physicochemical properties and experimental drying curves
Moisture content of fresh pitahayas was evaluated as 2.63± 0.15 kg water /kg dry matter. Total soluble solids were determined as 21.32±0.25 and 25.92±0.42 °Brix for fresh and osmo- dried pitahayas, respectively. Small seeds of the fruits were also part of the insoluble solids fraction (8.18 %).
Fig. 1 presents the experimental drying curves of pitahayas with and without osmotic dehydration. Since osmodehydrated samples have lower initial moisture content than fresh samples, process times needed to reach final water content is lower than those correspondents to untreated samples. Moreover, samples subjected to osmotic dehydration prior to convective drying has modified their internal structure affecting the action of different mass transport mechanisms, and thus contributing to enhance the water transport out of the solid [21]. Comparable results were reported for different foods subjected to osmotic dehydration like pumpkins [22] and pineapples [23].
3.2. Changes in water activity and volume samples
Fig. 2 and 3 present the variation of water activity and volume with process time during air dehydration at different temperatures, for pitahayas fruits with and without osmotic dehydration.
The measurement and prediction of water activity provide the best available tool for evaluating the stability of foods. Thus, the end point of drying is the residual moisture content of the final product which ensures economic viability and microbiological safety, i.e. a water activity value lower than 0.60 [24,25]. Therefore, according to Singh & Heldman [26], values of water activity among 0.20 and 0.40 ensures the stability of the product storage against browning and hydrolytically reactions, liquid oxidation and enzymatic activity. Regarding Fig. 2, treated and untreated samples had water activity values between 0.20 and 0.40, except 50 C.
Fig.
3 present the fruits volume variation (DV=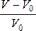 ) during processing. Both treated and untreated samples
exhibited changes in volume. Shrinkage of foodstuff during drying is
unavoidable because heating and removal of water from the food matrix may cause
stresses in the cellular structure, hence leading to structural collapse,
changes in volume, shape deformation and capillaries contraction [14].
) during processing. Both treated and untreated samples
exhibited changes in volume. Shrinkage of foodstuff during drying is
unavoidable because heating and removal of water from the food matrix may cause
stresses in the cellular structure, hence leading to structural collapse,
changes in volume, shape deformation and capillaries contraction [14].
Fruit with osmotic dehydration showed changes in volume lower that those only process by convective dehydration. Thus, osmodehydrated samples exhibited less shrinkage. Volume changes during OD are mainly due to compositional changes and mechanical stresses associated to mass fluxes [14]. Ideally, it can be considered that the shrinkage of the material is equal to the volume of the removed water. Therefore, a mathematical relationship can be obtained that relates the volume shrinkage to the moisture content of the material. According to Eq. (2), Table 1 shows the parameters related to this equation which showed satisfactory results (r2>0.9425).
Simulation of reduction of volume based on Eq.(2) indicated that shrinkage increases with decreasing moisture content in general, but shrinkage characteristics vary among drying products and drying methods. This is probably due to the unique biopolymer structure of individual agricultural product and the combined effect of process conditions that determines the type and extent of shrinkage [27].
3.3. Determination of water diffusion coefficient (Dwe)
Based on Fick's equation, effective diffusion coefficient (Dwe) can be calculated from Eqs. (4) and (6) for each work temperature. Estimated Dwe values are informed in Table 2.
It can be observed that moisture diffusion coefficients for pitahaya subjected to osmotic dehydration prior convective drying showed higher values than non-treated samples for all the temperatures under study. During osmotic dehydration, many aspects of cell structures are affected such as alteration of cell walls, splitting of the middle lamella, lysis of membranes, tissue shrinkage which could strongly influence the transport properties of the product during processing [28].
Comparable values were reported by other researchers related to osmodried fruits and vegetables: carambola [11], carrot cubes [29], West Indian cherry [30], apricots [16], apples [31], pomegranate arils [32] and Aloe Vera [33].
From the relationship of water diffusion coefficients and drying temperature, activation energy from the inverse slope of the line plot of ln Dwe versus T-1 can be obtained. In this research, activation energy values of 16.94 kJ/mol (r2=0.999) and 29.56 kJ/mol (r2=0.995) were obtained for untreated and treated samples, respectively. The Ea is a measure of dependence of the mass transfer process on temperature; lager magnitude of Ea is associated with higher temperature dependence. Higher activation energy therefore implies greater temperature sensitivity, and a smaller temperature change is needed for the mass transport to proceed more rapidly. The obtained values are within the range (0-63 kJ/mol) for diffusion-controlled processes [34].
Comparable values for activation energy were reported in previous works for watermelon [35]; mango [34] and pear [36].
3.4. Mathematical modeling of drying curves
Tables 3 shows the average values and standard deviations of the kinetic and empirical parameters ki (i = 1, 2), n, A, B, a and b, obtained for all the proposed models.
Except for de n and a, a tendency with increasing temperature was observed for each of the rest of the parameters, since an increase in drying air temperature showed an increase in the parameters values.
The a-parameter of Weibull is related to the velocity of the mass transfer at the beginning, e.g., the lower the a value, the faster the drying rate at the beginning [19]. In addition, parameter b decreases as temperature increases for both untreated and treated samples. Some authors suggested that parameter b represents the time needed to accomplish approximately 63% of the process [37]. Comparable results were reported in previous works for pepino fruit [6,19].
Regarding to parameter A for Peleg model, it shows a clear tendency to increase as temperature increases indicating that the higher the temperature the higher the water absorption rate. Similar tendencies for this parameter have been reported for chestnuts [38].
3.5. Statistical analysis of models
Table 4 shows the results of statistical tests (r2 and SSE) performed to the proposed models. These statistical tests evaluate the goodness of fit on the experimental data and they have been reported by other researchers during food drying analysis [19]. All the proposed models showed a good fit with high values of r2 (>0.90) and values close to zero for SSE. According to these results, the models that best fitted the experimental data, considering the statistical test applied, were the Peleg model (r2 = 0.9904; SSE= 0.0011) and Weibull (r2 =0.9957; SSE= 0.1040).
Therefore, Fig. 4 shows the experimental MR versus the corresponding estimate by the Weibull model to notice the goodness of fit of this mathematical model for all drying working temperatures, for both samples with and without osmotic dehydration. Similar observations were made by Cunha et al., (2001) modelling water losses during osmotic dehydration of apple [39], Corzo et al. (2008) [40] for air drying of coroba slices and Uribe et al., [19], for convective dehydration of pepino fruits.
4. Conclusion
Osmotic dehydration with sucrose 55 % (w/w) during 45 min was applied in order to evaluate the influence of pretreatment on convective drying rates of pitahayas at three different temperatures. Due to modifications in structure, osmodehydrated samples exhibited increasing drying rates with effective moisture coefficients greater that non-treated samples. Shrinkage due to variation in volume samples was more pronounced in untreated samples and was satisfactorily modeled by means of a polynomial equation. Different mathematical models were used to simulate experimental drying characteristics. Based on statistical results, the Peleg and Weibull models can be appropriate used to simulate experimental drying curves in the range of drying conditions under studied. Therefore, osmotic dehydration combined with convective dehydration provides an opportunity to produce novel shelf stable high quality pitahaya fruits for the local as well as for export markets.
Acknowledgements
The authors thank the Ministry of Agriculture and Rural Development of Colombia for the support provided to this article.
References
[1] Ayala-Aponte, A., Serna Cock, L. and Rodriguez-de la Pava, G., Moisture adsorption in yellow pitahaya (Selenicereus megalanthus). DYNA, 78 (170), pp.7-14, 2011.
[2] Beltran, M.C., Oliva-Coba, T.G., Gallardo-Velasquez, T. and Osorio-Revilla, G., Ascorbic acid, phenolic content and antioxidant capacity red, cherry, yellow and white types of pitahaya cactus fruit (Stenocereus stellatus Riccobono). Agrociencia, 43, pp. 153-162, 2009.
[3] Barbeu, G., The strawberry pear, a new tropical fruit. Fruits, 45, pp. 141-147, 1990.
[4] Wu, M.C. and Chen, C.S., Variation of sugar content in various parts of pitahaya fruit. Proceedings of the Florida State Horticultural Society, 110, pp. 225-227, 1997.
[5] Sacilik, K. and Elicin, A.K., The thin layer drying characteristics of organic apple slices. Journal of Food Engineering, 73 (3), pp. 281-289, 2006. https://doi.org/10.1016/j.jfoodeng.2005.03.024
[6] Doymaz, I., Convective drying kinetics of strawberry. Chemical Engineering and Processing, 47 (5), pp. 914-919, 2008. https://doi.org/10.1016/j.cep.2007.02.003
[7] Di Scala, K. and Crapiste, H., Drying kinetics and quality changes during drying of red pepper. LWT- Food Science and Technology, 41, pp. 789-795, 2008.
[8] Gomes, A., Lucena-Barbosa Jr., J., Colato, A.G. and Xidieh-Murr, F.E., Osmotic dehydration of acerola fruit (Malpighia punicifolia L.). Journal of Food Engineering 68, pp. 99-103, 2005. https://doi.org/10.1016/j.jfoodeng.2004.05.042
[9] Pereira-da Silva, W., Silva-do Amaral, D., Duarte, M., Mata, M., Silva, C., Pinheiro, R. and Pessoa, T., Description of the osmotic dehydration and convective drying of coconut (Cocos nucifera L.) Pieces: A three-dimensional approach. Journal of Food Engineering, 115, pp. 121-131, 2013. https://doi.org/10.1016/j.jfoodeng.2012.10.007
[10] Ashwini, N.B., Sowbhagya, H.B. and Rastogi, N.K., Osmotic dehydration assisted impregnation of curcuminoids in coconut slices. Journal of Food Engineering, 105 (3), pp. 453-459, 2011. https://doi.org/10.1016/j.jfoodeng.2011.03.002
[11] Ruiz-López, I.I., Ruiz-Espinosa, H., Herman-Lara, E. and Zárate-Castillo, G., Modeling of kinetics, equilibrium and distribution data of osmotically dehydrated carambola (Averrhoa carambola L.) in sugar solutions. Journal of Food Engineering 104, pp. 218-226, 2011. https://doi.org/10.1016/j.jfoodeng.2010.12.013
[12] ICONTEC. Norma Técnica Colombiana. NTC 3554. Frutas frescas. Pitahaya amarilla. Bogotá: ICONTEC, pp. 1-14, 1996.
[13] AOAC. Association of Official Analytical Chemists. Official method of analysis, Association of Official Analytical Chemists No. 934.06 (15th Ed), Arlington, MA, Washington, 1990.
[14] Mayor, L. and Sereno, A.M., Modelling shrinkage during convective drying of food materials: A review. Journal of Food Engineering, 61(3), pp. 373-386, 2004. https://doi.org/10.1016/S0260-8774(03)00144-4
[15] Ayala-Aponte, A., Giraldo, C.J. and Serna-Cock, L., Kinetics of osmotic dehydration of yellow pitahaya fruit (Selenicereus megalanthus). Interciencia, 35, pp. 539-544, 2010.
[16] Ispir, A. and Togrul, I.T., Osmotic dehydration of apricot: Kinetics and the effect of process parameters. Chemical Engineering Research and Design, 87, pp. 166-180, 2009. https://doi.org/10.1016/j.cherd.2008.07.011
[17] Crank, J., The mathematics of diffusion, second ed. Oxford University Press, London, UK, 1975.
[18] Peleg, M., An empirical model for the description of moisture sorption curves. Journal of Food Science, 53 (4), 1216-1219, 1998. https://doi.org/10.1111/j.1365-2621.1988.tb13565.x
[19] Uribe, E., Vega-Gálvez, A., Di Scala, K., Oyanadel, R., Saavedra, J. and Miranda, M., Characteristics of convective drying of pepino fruit (Solanum muricatum Ait.): Application of weibull distribution. Food and Bioprocess Technology, 4, pp. 1349-1356, 2011. https://doi.org/10.1007/s11947-009-0230-y
[20] Sharma, G.P. and Prasad, S., Effective moisture diffusivity of garlic cloves underging microwave-convective drying. Journal of Food Engineering, 65, pp. 609-617, 2004. https://doi.org/10.1016/j.jfoodeng.2004.02.027
[21] Chiralt, A. and Fito, P., Transport mechanisms in osmotic dehydration: The role of the structure. Food Science and Technology International, 9 (3), pp. 179-186, 2003. https://doi.org/10.1177/1082013203034757
[22] Garcia, C.C., Mauro, M.A. and Kimura, M. Kinetics of osmotic dehydration and air-drying of pumpkins (Cucurbita moschata). Journal of Food Engineering, 82 (3), pp. 284-291, 2007. https://doi.org/10.1016/j.jfoodeng.2007.02.004
[23] Lombard, G.E., Oliveira, J.C., Fito, P. and André, A., Osmotic dehydration of pineapple as a pre-treatment for further drying. Journal of Food Engineering, 85 (2), pp. 277-284, 2008. https://doi.org/10.1016/j.jfoodeng.2007.07.009
[24] Manjarres-Pinzón, K., Cortes-Rodriguez, M. and Rodríguez-Sandoval, E., Effect of drying conditions on the physical properties of impregnated orange peel. Brazilian Journal of Chemical Engineering, 30 (3), pp. 667-676, 2013. https://doi.org/10.1590/S0104-66322013000300023
[25] Proton, F. and Ahrné, L., Application of the Guggenheim, Anderson and De Boer model to correlate water activity and moisture content during osmotic dehydration of apples. Journal of Food Engineering, 61 (3), pp. 467-470, 2004. https://doi.org/10.1016/S0260-8774(03)00119-5
[26] Singh, R.P. and Heldman, D.R., Introduction to food engineering, 2nd ed. Academic Press, Inc., San Diego, pp.139-141, 1993.
[27] Ong, S.P. and Law, C.L., Hygrothermal properties of various foods, vegetables and fruits, in drying of foods, vegetables and fruits - Vol. 1, en Ed. Jangam, S.V., Law, C.L. and Mujumdar, A.S., ISBN - 978-981-08-6759-1, Published in Singapore, pp. 31-58, 2012.
[28] Azarpazhooh, E. and Ramaswamy, H., modeling and optimization of microwave osmotic dehydration of apple cylinders under continuous-flow spray mode processing conditions. Food and Bioprocess Technology, 5 (5), pp. 1486-1501, 2012. https://doi.org/10.1007/s11947-010-0471-9
[29] Singh, B., Kumar, A. and Gupta, A.K., Study of mass transfer kinetics and effective diffusivity during osmotic dehydration of carrot cubes. Journal of Food Engineering, 79 (2), pp. 471-480, 2007. https://doi.org/10.1016/j.jfoodeng.2006.01.074 https://doi.org/10.1016/j.jfoodeng.2006.01.073
[30] Silva, M., Da Silva, Z., Mariani, V. and Darche, S., Mass transfer during the osmotic dehydration of West Indian cherry. LWT - Food Science and Technology, 45(2), pp. 246-252, 2012.
[31] Souraki, B.A., Ghavami, M. and Tondro, H., Correction of moisture and sucrose effective diffusivities for shrinkage during osmotic dehydration of apple in sucrose solution. Food and Bioproducts Processing, 92 (1), pp. 1-8, 2014. https://doi.org/10.1016/j.fbp.2013.07.002
[32] Mundada, M., Bahadur-Singh, H. and Swati, M., Convective dehydration kinetics of osmotically pretreated pomegranate arils. Biosystems Engineering, 107, pp. 307-310, 2010. https://doi.org/10.1016/j.biosystemseng.2010.09.002
[33] Pisalkar, P.S., Jain, N.K. and Jain, S.K., Osmo-air drying of aloe vera gel cubes. Journal of Food Science and Technology, 48 (2), pp. 183-189, 2011. https://doi.org/10.1007/s13197-010-0121-2
[34] Alakali, J.S., Ariahu, C.C. and Nkpa, C.C., Kinetics of osmotic dehydration of mango. Journal of Food Processing and Preservation, 30, pp. 597-607, 2006. https://doi.org/10.1111/j.1745-4549.2006.00080.x
[35] Falade, G. and Ayanwuyi, F.A., Kinetics of mass transfer, and colour changes during osmotic dehydration of watermelon. Journal of Food Engineering, 80, pp. 979-985, 2007. https://doi.org/10.1016/j.jfoodeng.2006.06.033
[36] Park, J., Bin, A. and Reis-Brod, F.P., Drying of pear d'Anjou with and without osmotic dehydration. Journal of Food Engineering, 56, pp. 97-103 2002. https://doi.org/10.1016/S0260-8774(02)00152-8
[37] Marabi, A., Livings, S., Jacobsons, M. and Saguy, I.S., Normalized weibull distribution for modeling rehydration of food particulates. European Food Research Technology, 217, pp. 311-318, 2003. https://doi.org/10.1007/s00217-003-0719-y
[38] Moreira, R., Chenlo, F., Torres, M. and Vázques, G., Effect of stirring in the osmotic dehydration of chestnut using glycerol solutions. Journal of Food Science and Technology, 5, pp. 1507-1514, 2007.
[39] Cunha, L.M., Oliveira, F.A.R., Aboim, A.P. and Frías, J.M., Stochastic approach to the modelling of water losses during osmotic dehydration and improved parameter estimation. International Journal of Food Science and Technology, 36, pp. 253-262, 2001. https://doi.org/10.1046/j.1365-2621.2001.t01-1-00447.x
[40] Corzo, O., Bracho, N., Pereira, A. and Vásquez, A., Weibull distribution for modeling air drying of coroba slices. LWT-Food Science and Technology, 41(10), pp. 2023-2028, 2008. https://doi.org/10.1016/j.lwt.2008.01.002
A.A. Ayala-Aponte, received the BSc. Eng in Agricultural Engineering in 1993 from the Universidad del Valle, Cali, Colombia and the PhD degree in Science and Food Technology in 2011 from the Universidad Politécnica de Valencia, España. He is a professor in the area of Food Technology and Engineering, in the Universidad del Valle, Cali, Colombia. His research interests include: preservation and food processing.
L. Serna-Cock, received the BSc. in Bacteriology from the Universidad Católica de Manizales, Colombia in 1987, and the PhD degree in Food Engineering from the Universidad del Valle, Cali, Colombia. She is a professor in the area of Biotechnology in the Universidad Nacional de Colombia, Palmira, Colombia. Her research interests include: preservation, food processing and biotechnology.
J. Libreros-Triana, received the BSc. in Food Engineering from the Universidad del Valle, Cali, Colombia in 2010. She works in the food industry. Her research interests include: preservation and food processing.
C.M. Prieto, received the BSc. in Food Engineering from the Universidad del Valle, Cali, Colombia in 2010. She works in the food industry. Her research interests include: preservation and food processing.
K. Di Scala, received the BSc. Eng in Chemical Engineering in 1997 from the Universidad Nacional de Mar del Plata, Buenos Aires, Argentina, and the PhD degree in Chemical Engineering in 2006 from the Universidad Nacional del Sur, Bahía Blanca, Buenos Aires, Argentina. She is an assistant professor in the area of Food Engineering, in the Universidad Nacional de Mar del Plata Buenos Aires, Argentina. Her research interests include: food processing, food quality, and mathematical simulation and optimization of food processes.