
DOI: https://doi.org/10.15446/dyna.v82n193.46196
A methodology to obtain an analytical formula for the elastic modulus of lightweight aggregate concrete
Una metodología para obtener una fórmula analítica para el módulo de elasticidad del hormigón de áridos ligeros
Flávio de Souza-Barbosa a, Michèle Cristina Resende-Farage a, Aldemon Lage-Bonifácio a, Anne-Lise Beaucour b & Sophie Ortola c
a Faculdade de Engenharia, Universidade Federal de Juiz de Fora,
Juiz de Fora, Brazil. flavio.barbosa@ufjf.edu.br, michele.farage@ufjf.edu.br, aldemon.bonifacio@engenharia.ufjf.br
b Laboratoire de Mécanique et Matériaux du Génie Civil. Université de Cergy-Pointoise, Cergy-Pointoise,
France. anne-lise.beaucour@u-cergy.fr
c Laboratoire Energétique Mécanique
Electromagnétisme. Université
Paris Ouest Nanterre la Défense, Ville d'Avray, France. sophie.ortola@u-paris10.fr
Received: October 14th, 2014. Received in revised form: January 26th, 2015. Accepted: April 07th, 2015
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This work proposes a methodology to predict the elastic
modulus of lightweight aggregate concretes. To this end an analytical formula
is achieved by curve fitting experimental results from 135 concrete samples
made of 45 different mixes. The validation of the proposed methodology is
carried out by applying the obtained analytical formula to a set of 90 concrete
samples made of 30 different mixes. Comparisons with other methods applied to
predicting the elastic modulus of lightweight aggregate concretes indicate that
the results show good agreement and suggest that the proposed methodology could
be applied in practical situations.
Keywords: lightweight aggregate concrete; elastic modulus.
Resumen
Este trabajo propone una metodología para evaluar el
módulo elástico de los hormigones de agregados livianos. Para ello una fórmula
analítica se logra mediante el ajuste de la curva de los resultados
experimentales de 135 muestras de hormigón hechas de 45 mezclas diferentes. La
validación de la metodología propuesta se lleva a cabo mediante la aplicación
de la fórmula analítica obtenida a otro conjunto de 90 muestras de hormigón
hecha de 30 mezclas diferentes. Las comparaciones con otros métodos utilizados
para predecir el módulo de elasticidad de hormigones de agregados livianos
muestran que los resultados sean justos y sugieren que la metodología propuesta
podría aplicarse en situaciones prácticas.
Palabras clave: hormigón de áridos ligeros; módulo elástico.
1. Introduction
The structural application of Lightweight Aggregate Concrete (LWAC) is increasing around the world for economic and environmental reasons. The material leads to smaller dead loads, allowing lighter structural members and less amounts of reinforced steel, with no harm to safety. Due to this relatively recent tendency, many works have been dedicated to evaluate the long-term behavior of LWAC [1,2]. Another advantage of this kind of concrete is the fact that its thermal characteristics are normally attached to high levels of insulation [3].
On the other hand, mechanical properties of LWAC are frequently lower than those of ordinary concrete. For these reason, papers addressing the study of the elastic modulus, for instance, may be easily found in the literature [4-7]. Cui et al [5], for example, propose analytical formulas to evaluate LWAC elastic modulus based on a multiple linear regression analysis.
The present work aims to contribute to the practical application of LWAC, by proposing a methodology to achieve a simple analytical equation to evaluate the elastic modulus (Ec) of LWACs made of varied formulations.
It is well known that the elastic modulus plays a paramount role in structural design, since most of the practical applications adopt the theory of elasticity in the material modeling. Thus, it is very convenient for a structural engineer to dispose of a formula that supplies a reliable prevision of the elastic modulus of concrete. To this end a number of codes based on empirical formulas regarding LWAC are available in the literature - in which Ec is given in terms of two quantities: LWAC's characteristic compressive strength (fck) and oven-dry density of the LWAC (rs).
The American Concrete Institute - ACI [8] adopts expression 1:

The Eurocode 2 (EN 1992-1-1) [9] indicates equation 2:
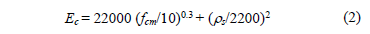
Where fcm (MPa) is the mean value of concrete compressive strength. In Eqs. 1-2, Ecand fck are given in MPa and rs in kg/m3.
Another approach for predicting the elastic modulus of a LWAC consists of expressions in terms of the lightweight aggregate (LWA) properties. For instance, Cui et al [5] suggest the analytical equation presented in Eq. (5), where the LWAC's Young modulus is evaluated as a function of the volumetric fraction of the aggregate (Va); the oven-dried density of the LWA (ra) and aggregate shape factor (Is).
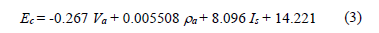
Where, ra is given in kg/m3; Va and Is are dimensionless.
It is also possible to predict concrete's mechanical properties by applying computational intelligence technics, such as Artificial Neural Network, Fuzzy Logic or Genetic Algorithms. Those kinds of methods require a set of experimental data in order to calibrate a computational based predictor and another set of laboratory results is applied to validate the quality of the adjusted numerical model. Several works in the literature deal with this strategy in order to predict concrete's mechanical properties [10,11].
The present work proposes an approach in which the evaluation of Ec is accomplished by using the oven-dry density (ra) of the lightweight aggregate (LWA); volumetric fraction of the aggregate (Va); and the Young modulus of the mortar (EM). The main advantage of the proposed methodology, when compared with Eqs. 1 and 2, is the fact that it does not demand previous knowledge of the concrete's compressive strength. Once the mortar elastic modulus is obtained, even for a different kind and/or amount of aggregate in the concrete, the proposed methodology is able to fairly predict Ec.
2. Proposed methodology
In order to predict Ec, the basic function presented in Eq. 5 was taken as a starting point, based on the parameters to be adjusted according to the experimental database:

Where EM is the elastic modulus of the mortar, standing for its influence on Ec, and G (l) represents the contribution of LWA for the Ec, where l = [(ra/1000)/Va].
Admitting that the mortar has an elastic modulus equal or superior to the LWA's, the maximum value of Ec should be EM and G (l) ≤ 1. The next step is to identify the function G (l). To this end, a set of experimental results, presented by Ke[M1] [12] in his PhD thesis, was used. Three kinds of mortar for five different types of LWA and five levels for the amount of concrete, resulting in 75 different mixes were tested. For each mix, three samples were tested, leading to 225 samples, and the mean values were named as Ec. Tab. 1 summarizes Ke's [12] results. In this table only the mean values for Ec (column Ec,exp in Table 1) are presented and fck is omitted. The concrete number (column # in Table 1) is followed by a letter (a, b or c) indicating the respective mortar. Two kinds of LWA were tested: expanded clay and shale. The oven-dry density (column rs in Table 1) is followed by the aggregate type: "A" for expanded clay and "B" for expanded shale. The shape factor (Is) for clay and shale are, respectively, 1.240 and 1.873.
Concretes from #1a to #45c were used to investigate function G (l). Figs 1 to 3 show a comparison between experimental results and Ec obtained with Eq. 5, considering G (l) as described in Eq. 6:

Where a = 30.82 m3/kg.
The parameter a is achieved by curve fitting Eq. 5, with G (l) showed in Eq. 6, for each analyzed mortar, resulting in three a parameters. The adopted value for a is the mean of them. The applied methodology for curve fitting was the mean square method.
3. Validation of the proposed methodology
By applying the achieved expression for Ec to the concretes from #46a to #75c the validation of the proposed methodology is carried out. Fig. 4 presents a comparison between the experimental results for Ec and the predicted counterparts.
It is possible to observe in Fig. 4 that the proposed methodology allows a good prediction for Ec.
4. Comparisons with available expressions
The performance of the proposed formula was assessed by comparing its results to those obtained from expressions available in the literature (Eqs. 1 and 2).
For comparison purposes, a multilayer perceptron artificial neural network was adopted, which is a technique applied to several kind of problems [13]. The network adopted herein has one hidden layer and eight neurons in the hidden layer. Concretes from #1 to #45 were used for the network training.
The performance of each predictor can be better observed in Figs. 5-9. In order to avoid distorted results in favor of the presented methodology, only the concretes used in the validation process were considered in these figures. For the proposed methodology, the neural network, and Cui et al [5] results, the predictions for Ec were multiplied by 0.85 aiming to consider a safety design parameter. This value was arbitrarily chosen and it tries to assure that practically all predictions for Ec are inferior to the experimental counterparts. For ACI and Eurocode, safety design coefficients are implicitly included in the respective Eqs. 1 and 2.
It is possible to observe from Figs. 5-9 that all formulations give conservative predictions for Ec for practically all concretes. Only a limited number of concretes had estimations for Ec slightly superior than the experimental counterparts.
THE results of the overall comparison are calculated in Table 2.
From Table 2 and Figs. 5-9 one can observe that:
Considering Tables 2 and 3, it is possible to conclude that, for the set of studied concretes, Eurocode, neural network and the present work present fair results for the prediction of Ec. Moreover, in view of the fact that the present work has the best performance in terms of maximum absolute error and the second best performance for the other two criteria, it is possible to consider that the fair results achieved by applying the proposed methodology are slightly better than the other methods.
5. Conclusions
The present work deals with an analytical expression to evaluate the elastic modulus of Lightweight Aggregate concretes,aimed towards practical applications by design engineers. The main feature of the proposed formula is the fact that the input parameters are: mortar Young's modulus, instead of concrete compressive strength; aggregate's density and amount of aggregate. The principal advantage of the proposed methodology is to avoid laboratory tests to determine concrete compressive strength for any prediction of Ec. Once the Young's modulus of the mortar is obtained, the estimation of Ec may be fairly achieved without further laboratory tests, even for different kinds or/and amounts of aggregates. The results for the set of analyzed concretes are considered as fair and the performance, when compared to other formulas, was slightly superior to Eurocode and neural network, and clearly superior to the other evaluated formulations.
Finally, It is important to observe that this article proposes a methodology and not an expression for the estimation of Ec. The results were achieved by analyzing two kinds of LWAs. A general formula demands more laboratory tests considering a large number of LWA types. Despite this, the proposed methodology could be applied for other kinds of aggregates, by adjusting a parameter for each LWA type. In the present work, the results were considered as fair for LWACs made by expanded clay and expanded shale, using the same adjusted a parameter. A separate analysis for each LWA would be less generic but more accurate.
Acknowledgements:
The authors would like to thank FAPEMIG (Fundação de Amparo à Pesquisa do Estado de Minas Gerais), CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) and CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior) for financial support.
References
[1] Youm, K.S, Jeong Y.J., Han E.S.H. and Yun, T.S., Experimental investigation on annual changes in mechanical properties of structural concretes with various types of lightweight aggregates. Construction and Building Materials, 73, pp. 442-451, 2014. DOI: 10.1016/j.conbuildmat.2014.09.044
[2] Bogas, J.A. and Cabaço, J.B., Long-term behaviour of concrete produced with recycled lightweight expanded clay aggregate concrete. Construction and Building Materials, 65, pp. 470-479, 2014. DOI: 10.1016/j.conbuildmat.2014.05.003
[3] Nguyen, L.H., Beaucour, A.-L., Ortola, S. and Noumowé, A., Influence of the volume fraction and the nature of fine lightweight aggregates on the thermal and mechanical properties of structural concrete. Construction and Building Materials, 51, pp. 121-132, 2014. DOI: 10.1016/j.conbuildmat.2013.11.019
[4] Ke, Y., Beaucour, A.L., Ortola, S., Dumontet, H. and Cabrillac, R., Influence of volume fraction and characteristics of lightweight aggregates on the mechanical properties of concrete. Construction and Building Materials, 23, pp. 2821-2828, 2009. DOI: 10.1016/j.conbuildmat.2009.02.038
[5] Cui, H.Z., Lo T.Y., Memon, S.A., Xing, F. and Shi, X., Analytical model for compressive strength, elastic modulus and peak strain of structural lightweight aggregate concrete. Construction and Building Materials, 36, pp. 1036-1043, 2012. DOI: 10.1016/j.conbuildmat.2012.06.041. DOI: 10.1016/j.conbuildmat.2012.06.034
[6] Zhang, M.H. and Gjorv, O., E. Mechanical properties of high-strength lightweight concrete. ACI Materials Journal, 88, pp. 240-247, 1991.
[7] Slate, F.O., Nilson, A.H. and Martinez, S., Mechanical properties of high-strength lightweight concrete. ACI Journal, Proceedings, 88, pp. 606-613, 1986.
[8] ACI 213R-03 - Guide for structural lightweight-aggregate concrete. American Concrete Institute standard, 2003.
[9] Eurocode. Design of concrete structures (EN 1992-1-1). 1992.
[10] Bilgehan, M., A comparative study for the concrete compressive strength estimation using neural network and neuro-fuzzy modelling approaches. Nondestruct Test Eva, 26, pp. 35-55, 2011. DOI: 10.1080/10589751003770100
[11] Yuan, Z., Wang, L-N. and Ji, X., Prediction of concrete compressive strength: Research on hybrid models genetic based algorithms and ANFIS. Advances in Engineering Software, 67, pp. 156-163, 2014. DOI: 10.1016/j.advengsoft.2013.09.004
[12] Ke, Y., Characterization of the mechanical behavior of lightweight aggregate concretes: Experiment and modelling, PhD. Thesis, Université de Cergy- Pontoise, 2008.
[13] Velasquez, H., Juan, D., Montoya, M. y Santiago, F., Modelado del indice de precios al consumidor usando um modelo hibrido basado en redes neuronales artificiales, DYNA rev.fac.minas, 72, pp.85-93, 2005.
F. de Souza-Barbosa, is an associate professor and research engineer at the Federal University of Juiz de Fora - UFJF, Brazil. He received his BSc. from UFJF, Brazil in 1994, MSc from Federal University of Rio de Janeiro - UFRJ, Brazil in 1996 and PhD. from UFRJ, Brazil, in 2000. He is member of the Editorial Board of the IABSE Journal - Structural Engineering International (SEI). His research interests include structural dynamics, concrete structures and computational modeling of structures.
M. C. Resende-Farage, is an associate professor and research engineer at the Federal University of Juiz de Fora - UFJF, Brazil. She received her BS from UFJF in 1991, M.Sc from Federal University of Rio de Janeiro - UFRJ in 1995 and Ph.D. from UFRJ in 2000. Her research interests include experimental analysis and computational modeling of concrete structures.
A. Lage-Bonifácio, is Ph.D. student in the graduation program in computational modeling in the Federal University of Juiz de Fora - UFJF, Brazil.
A.-L. Beaucour, is an associate professor at the University of Cergy-Pontoise, France. She graduated from the National School of Geology (ENSG) in 1993 and received her PhD in civil engineering from INSA de Lyon in 1997. Her research activities concern sustainable construction and high temperature behavior of concretes.
S. Ortola, is a lecturer at Paris Ouest Nanterre la Défense University, France. She received her BSc, MSc and PhD. in mechanics from Université Pierre & Marie Curie (UPMC, Paris6, France) in 1988, 1989 and 1992. Her research interests focus on modeling and numerical simulation of the behaviors of heterogeneous materials and structures. Applications concern constructions and building materials such as lightweight aggregate concrete or polymer mortar, subjected to thermo-mechanical solicitations