
DOI: https://doi.org/10.15446/dyna.v83n198.48654
Algorithm for wideband spectrum sensing based on sparse Fourier transform
Algoritmo para sensado de espectro de banda ancha basado en transformada dispersa de Fourier
Alexander López-Parrado ab & Jaime Velasco-Medina b
a GDSPROC Research Group, Universidad del Quindío, Armenia,
Colombia. parrado@uniquindio.edu.co
b Bionanoelectronics Research Group, Universidad
del Valle, Santiago de Cali, Colombia. jaime.velasco@correounivalle.edu.co
Received: January 27th, 2015. Received in revised form: August 07th, 2015. Accepted: March 11th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
In this paper we present a novel
sub-Nyquist algorithm to perform Wideband Spectrum Sensing (WSS) for Cognitive
Radios (CRs) by using the recently developed Sparse Fast Fourier Transform
(sFFT) algorithms. In this case, we developed a noise-robust sub-Nyquist WSS
algorithm with reduced sampling cost, by modifying the Nearly Optimal sFFT
algorithm; this was accomplished by using Gaussian windows with small support.
Simulation results show that the proposed algorithm is suitable for hardware
implementation of WSS systems for sparse spectrums composed of highly-noisy
multiband-signals.
Keywords: Cognitive Radio; Compressed Sensing; Sparse Fourier Transform; Spectrum Sensing.
Resumen
En
este trabajo se presenta un nuevo algoritmo sub-Nyquist para realizar Sensado
de Espectro de Banda Ancha (WSS) para Radios Cognitivos (CR) mediante el uso de
los algoritmos de Transformada Dispersa de Fourier (sFFT) recientemente
desarrollados. En este caso, hemos desarrollado un algoritmo sub-Nyquist
robusto ante el ruido para WSS con reducción en el costo de muestreo, mediante
la modificación del algoritmo sFFT casi óptimo; esto se logró mediante el uso
de ventanas Gaussianas con soporte pequeño. Los resultados de simulación
muestran que el algoritmo propuesto es adecuado para la implementación hardware
de sistemas WSS sobre espectros dispersos compuestos por señales multibanda
altamente ruidosas.
Palabras clave: Radio Cognitiva; Sensado Compresivo; Transformada Dispersa de Fourier; Sensado de Espectro.
1. Introduction
Cognitive Radio (CR) is becoming the new paradigm for developing the next generation of radio communication systems. CR addresses the issue of spectrum misuse of current radio communication systems by adding cognitive features to the radios such as: spectrum sensing (SS), power control and spectrum management [1,2]. These features are initially presented in the IEEE 802.22 [3] standard, which was developed in 2011 by the Institute of Electrical and Electronics Engineers (IEEE) and defines a Wireless Regional Area Network (WRAN) that uses the Very High Frequency (VHF) and Ultra High Frequency (UHF) television (TV) bands by considering cognitive radio capabilities.
One technical challenge in CR is the efficient implementation of the SS function for a higher bandwidth by minimizing the required sampling rate. The SS function detects Primary Users (PUs) or Secondary Users (SUs) in some regions of the spectrum, allowing an opportunistic usage of the available bands. The IEEE 802.22 standard has an informative annex that defines two categories of SS techniques: blind sensing and signal specific sensing. Blind sensing techniques use energy measures, and signal specific sensing techniques use preambles and pilot signals. However, these sensing techniques are narrowband because they can only sense a single carrier frequency.
On the one hand, measurements carried out by the Microsoft Spectrum Observatory at Washington DC [4] show that around 3% of the band between 30 MHz and 3 GHz is used sparsely to host most of the worldwide radio services [4]. This sparse occupancy of the radio electric spectrum has motivated the theoretical research about Wideband Spectrum Sensing (WSS) techniques during the last five years [5-7]. In this case, the research results have shown that sub-Nyquist sampling techniques such as Analog to Information Conversion (AIC) [6],[8], Modulated Wideband Conversion (MWC) [6][10] and Multi Coset (MC) sampling [6],11,12] are promissory candidates for developing WSS systems as the shown in Fig. 1
The sub-Nyquist WSS systems are usually composed of a sub-Nyquist sampler, a spectral reconstruction block and a decision stage [5,6[9]. The spectral reconstruction block is usually constructed by using Compressive Sensing (CS) techniques [13,14].
On the other hand, spectral reconstruction considering the Sparse Fast Fourier Transform (sFFT) algorithms [15-19] has not been well developed as these algorithms either require a high sampling cost for typical spectrum occupancy [15,16,[19], they are very noise sensitive [17], or they are too complex [18].
In the context of WSS algorithms, the challenge is to achieve sub-Nyquist sampling rates using low-power and low-speed ADCs for highly-noisy signals. Thus, considering the above, the main contribution of this paper is the design of a new sub-Nyquist WSS algorithm that reduces the sampling cost by using a modified version of the sFFT algorithm with Gaussian small support windows. This proposed algorithm is very suitable for hardware implementation of WSS systems using ASICs or FPGAs, and to the best of our knowledge, it is the first that uses the recently developed Nearly Optimal Sparse Fourier Transform.
The rest of the paper is organized as follows: Section 2 presents some mathematical basics about the sub-Nyquist WSS algorithm we developed, Section 3 describes the proposed sub-Nyquist WSS algorithm, Section 4 presents simulation results performed on scenarios composed of highly-noisy multiband-signals, and, Section 5, presents our conclusions and suggestions for future work.
2. Mathematical background
In this section, we present some fundamental concepts about the sub-Nyquist sFFT algorithm we developed. First, we explain some basics about DFT and sparse signals, and second, we describe the mathematical tools pseudo-random spectral permutation, filtering window, and hashing function.
2.1. Discrete Fourier transform and sparsity
Given a discrete time signal  of length
of length 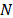 , its
, its 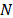 -point Discrete Fourier Transform (DFT)
-point Discrete Fourier Transform (DFT)  is defined in Eq. (1).
is defined in Eq. (1).

Where 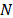 is a power of two,
is a power of two,  denotes the set of indexes
denotes the set of indexes , and
, and 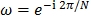 is the
is the 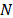 -th root of unity. In this case, the
number of non-zero elements of the vector
-th root of unity. In this case, the
number of non-zero elements of the vector  is called the sparsity order
is called the sparsity order  and is defined in Eq. (2).
and is defined in Eq. (2).
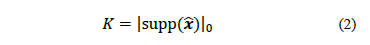
Where 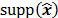 is the set of indexes of the
non-zero elements of the vector
is the set of indexes of the
non-zero elements of the vector  , and
, and  represents the
represents the 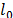 -norm of the vector. Then, a time domain signal
-norm of the vector. Then, a time domain signal 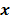 is sparse in the DFT domain
if
is sparse in the DFT domain
if  .
.
In this context, a set of algorithms called sFFT takes advantage of the signal sparsity in the DFT domain to speed up the runtime of the Fast Fourier Transform (FFT) algorithms used to calculate the DFT [15-18]. These sFFT algorithms, like the Nearly Optimal sFFT algorithm presented in [16], use the following mathematical tools: pseudo-random spectral permutation [15-19], filtering window [16] and hashing function [15,16].
2.2. Pseudo-random spectral permutation
This permutation isolates spectral components from each other [19] and is performed as described in Eq. (3).

Where  and
and  are the permuted spectrum signals in the time domain and the DFT
domain, respectively;
are the permuted spectrum signals in the time domain and the DFT
domain, respectively;  is the spectral permutation
function; and
is the spectral permutation
function; and  and
and  are the spectral permutation
parameters. The spectral permutation function translates the frequency bin from
the
are the spectral permutation
parameters. The spectral permutation function translates the frequency bin from
the 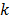 -th location to the
-th location to the 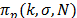 -th location, in this case
-th location, in this case  mod
mod 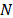 exists for all odd
exists for all odd  if
if  is a power of two. The sFFT algorithm randomly chooses the spectral
permutation parameters
is a power of two. The sFFT algorithm randomly chooses the spectral
permutation parameters  and
and  from a uniform distribution.
Thus, the spectral permutation with these pseudo-random parameters is related
to a pseudo-random sampling scheme [15-19].
from a uniform distribution.
Thus, the spectral permutation with these pseudo-random parameters is related
to a pseudo-random sampling scheme [15-19].
2.3. Filtering window
The
filtering window is a new mathematical tool that reduces the size of the FFT
from points 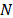 to
to  This is accomplished in the Nearly Optimal
sFFT algorithm by extending a flat passband region of width
This is accomplished in the Nearly Optimal
sFFT algorithm by extending a flat passband region of width  around each sparse component; this approach
replaces the filter bank of previous sFFT algorithms [19,20] and avoids the use of non-equispaced
data FFTs [21]. Nonetheless, this flat window has a
support that is not small enough to achieve sub-Nyquist sampling rates.
around each sparse component; this approach
replaces the filter bank of previous sFFT algorithms [19,20] and avoids the use of non-equispaced
data FFTs [21]. Nonetheless, this flat window has a
support that is not small enough to achieve sub-Nyquist sampling rates.
Thus, in order to reduce the sampling
cost of the sFFT algorithm, we designed a small support window 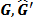 such that
such that  ; nevertheless, this small support can reduce the accuracy, which is
not a big issue in the case of WSS systems. In this case, the window in the
time domain is designed with an ideal low-pass filter using a Gaussian window
with finite duration to truncate the impulse response. The cutoff frequency of
the low-pass filter is
; nevertheless, this small support can reduce the accuracy, which is
not a big issue in the case of WSS systems. In this case, the window in the
time domain is designed with an ideal low-pass filter using a Gaussian window
with finite duration to truncate the impulse response. The cutoff frequency of
the low-pass filter is 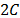 , where
, where  , and the standard deviation
, and the standard deviation  of the Gaussian window is
obtained from the 68-95-99.7 rule [22], as
described in Eq. (4).
of the Gaussian window is
obtained from the 68-95-99.7 rule [22], as
described in Eq. (4).
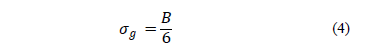
Eq. (5)-(6) describe the Gaussian window in the time domain and the DFT domain, respectively.

Where vector 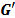 is the approximated window
and
is the approximated window
and 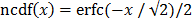 is the Normal Cumulative
Distribution Function [23].
is the Normal Cumulative
Distribution Function [23].
The Gaussian window is normalized both in the time domain and the DFT domain in order to achieve unit DC gain, and its total bandwidth in DFT domain is given by Eq. (7).

Finally, the windowing process is described in Eq. (8), and it is performed in the time domain after the pseudo-random spectral permutation is carried out.

Where,  is the windowed signal in the
time domain.
is the windowed signal in the
time domain.
2.4. Hashing function
The hashing
function obtains  points from the
points from the 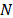 -point spectrum of the signal
-point spectrum of the signal  , these points are separated by
, these points are separated by  bins, and they are obtained by calculating the
bins, and they are obtained by calculating the  -point DFT of the sub-sampled signal
obtained from
-point DFT of the sub-sampled signal
obtained from  . The vector that has the hashes of
signal
. The vector that has the hashes of
signal  is
is  and it is calculated using Eq. (9) [15,16].
and it is calculated using Eq. (9) [15,16].
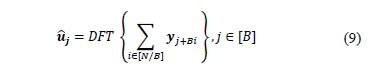
From Eq. (7)-(9), it
is possible to note that for each sparse component of the signal 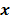 there are 14 non-zero hashes
located in the offsets given by Eqs. (10) and (11).
there are 14 non-zero hashes
located in the offsets given by Eqs. (10) and (11).

Where  and
and  are the 14 indexes of the
hashes
are the 14 indexes of the
hashes  for each hashed single sparse
component, and
for each hashed single sparse
component, and  is the floor-hash function
and
is the floor-hash function
and  is the ceil-hash function.
is the ceil-hash function.
Finally, it has to be noted that the use of pseudo-random spectral permutation and small support windows leads to a sub-Nyquist random sampling scheme; where, under certain conditions, the average sampling rate is below Nyquist.
3. Sub-Nyquist wideband spectrum sensing algorithm
In this section, we describe the Sub-Nyquist WSS algorithm, called SNSparseWSS, which presents a reduced sampling rate compared to the sFFT algorithm described in [16]. This improvement is achieved by using the window described in the past section and by performing several modifications to the procedures presented in [16].
The SNSparseWSS algorithm, described in Alg. 1,
calculates the spectrum occupancy 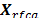 with constant False Alarm
Probability (
with constant False Alarm
Probability (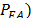 [2],[11], and
has the following input parameters: the sparse bandwidth
[2],[11], and
has the following input parameters: the sparse bandwidth  in Hz, the total bandwidth
in Hz, the total bandwidth  in Hz, the duration of the
sensing window
in Hz, the duration of the
sensing window  in seconds, the noise power
in seconds, the noise power  , and the constants of the sFFT algorithm
, and the constants of the sFFT algorithm 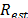 and
and  [16].
[16].
The algorithm calculates the spectrum
occupancy using four processing stages: the first one performs sub-Nyquist
sampling on the wideband complex signal  ; the second one locates the sparse components by using the vector
; the second one locates the sparse components by using the vector  , the set of permutation parameters
, the set of permutation parameters  , and the modified LocateSignal procedure [16],[24]; the
third one estimates the DFT values by using the vector
, and the modified LocateSignal procedure [16],[24]; the
third one estimates the DFT values by using the vector 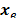 , the set of permutation parameters
, the set of permutation parameters 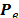 , and the modified EstimateValues procedure [15]; and
the fourth one detects the occupied bands with constant
, and the modified EstimateValues procedure [15]; and
the fourth one detects the occupied bands with constant  using the ConstantPfaRecovery procedure, which
determines whether a channel is occupied or not by a PU. Therefore, it is
necessary to test two spectrum sensing hypotheses,
using the ConstantPfaRecovery procedure, which
determines whether a channel is occupied or not by a PU. Therefore, it is
necessary to test two spectrum sensing hypotheses,  for vacant channel and
for vacant channel and  for occupied channel [2], by
using a detector with constant
for occupied channel [2], by
using a detector with constant [2],[11] as
described in Eq. (12) [11].
[2],[11] as
described in Eq. (12) [11].

Where,  is the decision threshold.
is the decision threshold.
3.1. Modified procedures
We modified the HashToBins, LocateSignal, LocateInner, and EstimateValues procedures described in [16] in order to use the proposed filtering window and to reduce the execution time.
3.1.1. HashToBins procedure
This procedure,
presented in Alg. 2, calculates the hashes-error by
subtracting the hashes of the instantaneous estimation  from the hashes
from the hashes  [16], and it has the following input
parameters: the time domain signal
[16], and it has the following input
parameters: the time domain signal 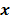 ; the instantaneous estimation
; the instantaneous estimation  of
of  ; the parameter
; the parameter  ; the spectral permutation parameters
; the spectral permutation parameters  , and
, and  ; and the vectors
; and the vectors 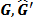 of the filtering window in the time domain and
the DFT domain respectively.
of the filtering window in the time domain and
the DFT domain respectively.
This procedure calculates the
hashes-error using three processing stages: the first one simultaneously
calculates in the time domain the pseudo-random spectral permutation, the
windowing, and the hashing process; the second calculates the DFT domain hashes  by performing the
by performing the  -point FFT of the time domain hashes
-point FFT of the time domain hashes 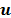 ; and the third one calculates the hashes-error by subtracting the
DFT domain hashes of
; and the third one calculates the hashes-error by subtracting the
DFT domain hashes of  from the hashes
from the hashes  , in this case there are 14 hashes for each sparse component in
, in this case there are 14 hashes for each sparse component in  .
.
3.1.2. LocateSignal procedure
This procedure, presented in Alg. 3,
calculates the set  of frequency bins corresponding to
of frequency bins corresponding to  sparse components found in
sparse components found in 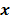 ; and it has the following input parameters: the time domain signal
; and it has the following input parameters: the time domain signal 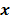 ; the instantaneous estimation
; the instantaneous estimation  of
of  ; the parameter
; the parameter  ; the spectral permutation parameters
; the spectral permutation parameters  the vectors
the vectors 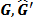 of the filtering
window in the time domain and the DFT domain respectively; the threshold
constant for location
of the filtering
window in the time domain and the DFT domain respectively; the threshold
constant for location  [16]; and
the number of location iterations
[16]; and
the number of location iterations 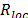 [16].
[16].
This procedure locates the sparse
components of 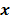 using four processing stages:
the first one sets the initial conditions, the second one adjusts the frequency
locations, the third one reduces the search region, and the fourth one inverts
the spectral permutation. The setting of initial conditions is performed by
first calculating a reference hashes vector
using four processing stages:
the first one sets the initial conditions, the second one adjusts the frequency
locations, the third one reduces the search region, and the fourth one inverts
the spectral permutation. The setting of initial conditions is performed by
first calculating a reference hashes vector  ; second pre-calculating an initial guess of value
; second pre-calculating an initial guess of value  of frequency locations in the
permuted spectrum; and third by pre-calculating the initial values of
of frequency locations in the
permuted spectrum; and third by pre-calculating the initial values of  ,
,  , and
, and  , where
, where  is the width of the region
for searching the frequency adjustment,
is the width of the region
for searching the frequency adjustment,  is the number of candidate
adjustments in
is the number of candidate
adjustments in  ,
,  is the number of
is the number of
adjustments, and 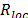 is the number of location iterations for each
adjustment. The adjustment of frequency locations is performed by using
is the number of location iterations for each
adjustment. The adjustment of frequency locations is performed by using  times the procedure LocateInner. The reduction of the search region is performed by
dividing
times the procedure LocateInner. The reduction of the search region is performed by
dividing  by a factor
by a factor 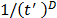 at the
at the  -th adjustment, this reduction allows
a systematic refining of the frequency location. Finally, the spectral
permutation inversion is performed by calculating the function
-th adjustment, this reduction allows
a systematic refining of the frequency location. Finally, the spectral
permutation inversion is performed by calculating the function  on each located frequency.
on each located frequency.
3.1.3. LocateInner procedure
This
procedure, presented in Alg. 4, calculates the adjustment  of the frequency locations in the permuted
spectrum, and it has the following input parameters: the time domain signal
of the frequency locations in the permuted
spectrum, and it has the following input parameters: the time domain signal 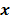 ; the instantaneous estimation
; the instantaneous estimation  of
of  ; the parameter
; the parameter  ; the spectral permutation parameters
; the spectral permutation parameters  ,
,  , and
, and  ; the vectors
; the vectors 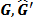 of the filtering window in the time domain and
the DFT domain respectively; the threshold constant for location
of the filtering window in the time domain and
the DFT domain respectively; the threshold constant for location  ; the number of location iterations
; the number of location iterations 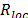 ; the width of search region
; the width of search region  ; the number of candidate adjustments
; the number of candidate adjustments  ; the reference hashes vector
; the reference hashes vector  ; and the current estimation of
frequency locations
; and the current estimation of
frequency locations  .
.
This procedure performs the adjustment of
the frequency location using five processing stages: the first one sets the
initial conditions, the second calculates the hashes-error, the third
calculates the angles of the hashes-error and candidate frequency bins, the
fourth performs the voting stage, and the fifth locates the frequency bins. The
setting of initial conditions clears the vote counters of the  candidate adjustments for the
candidate adjustments for the  candidate frequency bins. The
hashes calculation stage obtains
candidate frequency bins. The
hashes calculation stage obtains  hashes vectors
hashes vectors 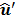 , which are calculated from the signal
, which are calculated from the signal 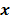 by using the HashToBins procedure with pseudo-random
permutation parameters of the form
by using the HashToBins procedure with pseudo-random
permutation parameters of the form  . The angle calculation stage obtains the vector
. The angle calculation stage obtains the vector  , which represents the angle differences between the reference
hashes
, which represents the angle differences between the reference
hashes  and the hashes
and the hashes 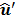 . The voting stage increments the vote counter
. The voting stage increments the vote counter 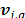 corresponding
corresponding
to the  -th frequency bin and
-th frequency bin and 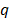 -th adjustment, if Eq. (13) is
satisfied.
-th adjustment, if Eq. (13) is
satisfied.

Where  is the angle of the
is the angle of the  -th candidate frequency bin for the
-th candidate frequency bin for the 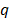 -th adjustment, that is,
-th adjustment, that is,  is related to the
is related to the 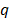 -th candidate frequency adjustment
-th candidate frequency adjustment  . Additionally, the above calculation
converges if
. Additionally, the above calculation
converges if  is chosen at random from the set
is chosen at random from the set 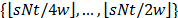 with enough small threshold
with enough small threshold  . Finally, the frequency location stage selects the minimum
. Finally, the frequency location stage selects the minimum 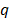 from the set
from the set  ; thus the estimated
; thus the estimated  -th permuted-frequency bin is refined
using Eq. (14).
-th permuted-frequency bin is refined
using Eq. (14).
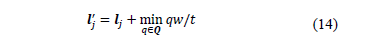
3.1.4. EstimateValues procedure
This procedure, presented in Alg. 5, calculates
the DFT estimation adjustment  , and it has the following input parameters: the time domain signal
, and it has the following input parameters: the time domain signal 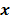 ; the instantaneous estimation
; the instantaneous estimation  of
of  ; the parameter
; the parameter  ; the spectral permutation parameters
; the spectral permutation parameters  the vectors
the vectors 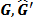 of the filtering window in
the time domain and the DFT domain respectively; the set of located sparse
components
of the filtering window in
the time domain and the DFT domain respectively; the set of located sparse
components  ; the number of sparse components to estimate
; the number of sparse components to estimate  ; and the number of estimation iterations
; and the number of estimation iterations 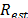 [16]. This
procedure calculates the DFT estimation adjustment
[16]. This
procedure calculates the DFT estimation adjustment  using three processing
stages: the first one calculates the
using three processing
stages: the first one calculates the  sets of hashes-error from the signal
sets of hashes-error from the signal 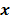 by using the HashToBins
procedure and considering different pseudo-random permutation parameters; the
second one separately calculates the median of the real and imaginary parts of
the calculated hashes-error by only considering the set of located sparse
frequency bins in
by using the HashToBins
procedure and considering different pseudo-random permutation parameters; the
second one separately calculates the median of the real and imaginary parts of
the calculated hashes-error by only considering the set of located sparse
frequency bins in  , and by cancelling the pseudo-random spectral permutation and the
effect of the windowing in the DFT domain; and the third one saves the
, and by cancelling the pseudo-random spectral permutation and the
effect of the windowing in the DFT domain; and the third one saves the  most energetic components
most energetic components  .
.
4. Simulation results of SNSparseWSS algorithm
This section presents the simulation results of the SNSparseWSS algorithm for sub-Nyquist sampling and verification results for Wideband Spectrum Sensing.
4.1. Sub-Nyquist capabilities
In order to verify the sampling cost, we
need to know all the spectral permutation parameters 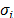 and
and  that are pseudo-randomly
generated by the SNSparseWSS algorithm; thus, the set of sampling points can be
calculated using Eq. (15).
that are pseudo-randomly
generated by the SNSparseWSS algorithm; thus, the set of sampling points can be
calculated using Eq. (15).
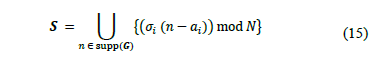
Considering the set of sampling points  , it is possible to calculate the average sampling rate
, it is possible to calculate the average sampling rate  of the SNSparseWSS algorithm using Eq. (16).
of the SNSparseWSS algorithm using Eq. (16).
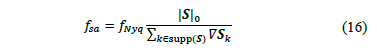
Where,  is the Nyquist frequency, and
is the Nyquist frequency, and  is a finite-backward
difference to estimate the average separation between samples. Fig. 2 shows
the percentage of Nyquist frequency versus the percentage of spectrum occupancy
for the SNSparseWSS algorithm.
is a finite-backward
difference to estimate the average separation between samples. Fig. 2 shows
the percentage of Nyquist frequency versus the percentage of spectrum occupancy
for the SNSparseWSS algorithm.
From Fig. 2, we
can see that the algorithm reaches a sampling rate of close to  for a spectrum occupancy
between 2% and 3%; thus, for typical scenarios where the spectrum occupancy is
close to 2% the SNSparseWSS algorithm
is very suitable for implementing sub-Nyquist WSS systems and its performance
is comparable to the WSS systems based on MC sampling [11].
for a spectrum occupancy
between 2% and 3%; thus, for typical scenarios where the spectrum occupancy is
close to 2% the SNSparseWSS algorithm
is very suitable for implementing sub-Nyquist WSS systems and its performance
is comparable to the WSS systems based on MC sampling [11].
4.2. Verification of the SNSparseWSS algorithm
In order to verify the WSS capabilities
of the SNSparseWSS algorithm, we considered as test vehicle a highly-noisy
multiband-signal scenario composed of 5 time domain signals located in the
center frequencies 317-576-1300-984-163 MHz, and a total bandwidth  of 1.5 GHz. Each signal has a
bandwidth of 5 MHz, is composed of random 4-QAM symbols that are filtered using
a raised cosine filter with roll-off factor r = 0.5, and has SNR values from -5
dB to 5 dB. The test signal with SNR=-5 dB is shown in Fig. 3.
of 1.5 GHz. Each signal has a
bandwidth of 5 MHz, is composed of random 4-QAM symbols that are filtered using
a raised cosine filter with roll-off factor r = 0.5, and has SNR values from -5
dB to 5 dB. The test signal with SNR=-5 dB is shown in Fig. 3.
In this case, the duration of the
spectrum sensing window is  which implies that an FFT
with
which implies that an FFT
with  must be used, and the total
sparse bandwidth is 25 MHz (5 signals
must be used, and the total
sparse bandwidth is 25 MHz (5 signals  5 MHz) which leads to a
sub-sampled FFT with
5 MHz) which leads to a
sub-sampled FFT with  . The algorithm was parameterized with
. The algorithm was parameterized with 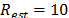 estimation iterations and a
location threshold of
estimation iterations and a
location threshold of  , with these settings the SNSparseWSS algorithm achieves an average sampling rate of
, with these settings the SNSparseWSS algorithm achieves an average sampling rate of  .
.
Fig. 4 shows the recovered spectrum using
the SNSparseWSS algorithm. In this
figure, we can see that the Gaussian small support window increases the total
error of estimated DFT value; this issue can be mitigated using appropriate
settings for the constant  detector, which implies that the occupied
channels can be detected with constant
detector, which implies that the occupied
channels can be detected with constant [11].
[11].
Fig. 5 shows
the WSS simulation results using the constant  detector with
detector with  In this figure, we can see that the algorithm
can perform WSS by detecting the occupied channels by the Pus. If additional
information about the multiband-signal is available, such as the minimum
channel separation
In this figure, we can see that the algorithm
can perform WSS by detecting the occupied channels by the Pus. If additional
information about the multiband-signal is available, such as the minimum
channel separation  [11], the detection can be improved by
reducing the
[11], the detection can be improved by
reducing the  .
.
Fig. 6 shows
simulation results for the false alarm probability with SNR values of -5 dB,
-2.5 dB, 0 dB, 2.5 dB, and 5 dB. In this figure we can see that the  is approximately constant
regardless the SNR of the multiband-signals.
is approximately constant
regardless the SNR of the multiband-signals.
5. Conclusions and future work
In this paper, we present the design of a novel algorithm for sub-Nyquist Wideband Spectrum Sensing based on a modified Nearly Optimal sFFT algorithm. This WSS algorithm was verified using several tests. From the verification results we can conclude that the proposed algorithm is suitable for implementing the spectrum sensing function of wideband cognitive radios in highly-noisy environments. To the best of our knowledge, the proposed WSS algorithm is the first that uses the new Nearly Optimal Sparse Fourier Transform algorithm, and it has a reduced sampling cost by using flat Gaussian small support windows and modified procedures.
Future work will addressed efficient hardware implementation of the modified Nearly Optimal sFFT algorithm using an FPGA.
Acknowledgements
Alexander López Parrado thanks Colciencias for the scholarship, and he also thanks Universidad del Quindío for the study commission.
References
[1] Mitola, J. and Maguire, G.Q., Cognitive radio: Making software radios more personal. IEEE Personal Communications, 6(4), pp. 13-18, 1999. DOI: 10.1109/98.788210.
[2] Arslan, H., Cognitive radio, software defined radio, and adaptive wireless systems. Dordrecht: Springer, 2007. DOI: 10.1007/978-1-4020-5542-3.
[3] IEEE. IEEE 802.22-2011, wireless regional area networks (wran) - specific requirements part 22: Cognitive wireless ran medium access control (mac) and physical layer (phy) specifications: Policies and procedures for operation in the tv bands. 2011. DOI: 10.1109/IEEESTD.2011.5951707.
[4] M.T.P. Group, Microsoft spectrum observatory, [online], Seattle, [Date of reference, Nov. 2013.]. Available at: http://spectrum-observatory.cloudapp.net/.
[5] Vito, L.D., A review of wideband spectrum sensing methods for cognitive radios, Proceedings of Instrumentation and Measurement Technology Conference (I2MTC), pp. 2257-2262, 2012. DOI: 10.1109/I2MTC.2012.6229530.
[6] Hongjian, S., Nallanathan, A., Wang, C.X. and Chen, Y., Wideband spectrum sensing for cognitive radio networks: a survey. IEEE Wireless Communications, 20(2), pp. 74-81, 2013. DOI: 10.1109/MWC.2013.6507397.
[7] Axell, E., Leus, G., Larsson, E.G. and Poor, H.V., Spectrum sensing for cognitive radio: State-of-the-art and recent advances. IEEE Signal Processing Magazine, 29(3), pp. 101-116, 2012. DOI: 10.1109/MSP.2012.2183771.
[8] Laska, J., Kirolos, S., Duarte, M., Ragheb, T., Baraniuk, R. and Massoud, Y., Theory and implementation of an analog-to-information converter using random demodulation, Proceedings of IEEE International Symposium on Circuits and Systems, pp. 1959-1962, 2007. DOI: 10.1109/ISCAS.2007.378360.
[9] Sun, H., Chiu, W.Y., Jiang, J., Nallanathan, A. and Poor, H.V., Wideband spectrum sensing with Sub-Nyquist sampling in cognitive radios. IEEE Transactions on Signal Processing, 60(11), pp. 6068-6073, 2012. DOI: 10.1109/TSP.2012.2212892.
[10] Mishali, M. and Eldar, Y.C., From theory to practice: Sub-nyquist sampling of sparse wideband analog signals. IEEE Journal of Selected Topics in Signal Processing, 4(2), pp. 375-391, 2010. DOI: 10.1109/JSTSP.2010.2042414.
[11] Yen, C.-P., Tsai, Y. and Wang, X., Wideband spectrum sensing based on Sub-Nyquist sampling. IEEE Transactions on Signal Processing, 61(12), pp. 3028-3040, 2013. DOI: 10.1109/TSP.2013.2251342.
[12] Tsui, J.B., Digital techniques for wideband receivers, 2nd Edition. Raleigh: Scitech, 2004. DOI: 10.1049/SBRA005E.
[13] Donoho, D.L., Compressed sensing. IEEE Transactions on Information Theory, 52(4), pp. 1289-1306, 2006. DOI: 10.1109/TIT.2006.871582.
[14] Lobato-Polo, A.P., Ruiz-Coral, R.H., Quiroga-Sepúlveda, J.A. and Recio-Vélez, A.L., Sparse signal recovery using orthogonal matching pursuit (OMP). Ingeniería e Investigación, 29(2), pp. 112-118, 2009.
[15] Hassanieh, H., Indyk, P., Katabi, D. and Price, E., Simple and practical algorithm for sparse fourier transform, Proceedings of ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 1183-1194, 2012. DOI: 10.1137/1.9781611973099.93.
[16] Hassanieh, H., Indyk, P., Katabi, D. and Price, E., Nearly optimal sparse fourier transform, Proceedings of the 44th symposium on Theory of Computing (STOC), pp. 563-578, 2012. DOI: 10.1145/2213977.2214029.
[17] Hassanieh, H., Shi, L., Abari, O., Hamed, E. and Katabi, D., Ghz-wide sensing and decoding using the sparse fourier transform, Proceedings of IEEE INFOCOM, pp. 2256-2264, 2014. DOI: 10.1109/INFOCOM.2014.6848169.
[18] Indyk , P., Kapralov, M. and Price, E., (Nearly) Sample-optimal sparse fourier transform, Proceedings of ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 480-499, 2014. DOI: 10.1137/1.9781611973402.36.
[19] Gilbert, A.C., Strauss, M.J. and Tropp, J.A., A tutorial on fast fourier sampling. IEEE Signal Processing Magazine, 25(2), pp. 57-66, 2008. DOI: 10.1109/MSP.2007.915000.
[20] Gilbert, A.C., Muthukrishnan, S. and Strauss, M.J., Improved time bounds for near-optimal sparse fourier representations, Proceedings of SPIE Wavelets XI, pp. 1-15, 2005. DOI: 10.1117/12.615931.
[21] Dutt, A. and Rokhlin, V., Fast fourier transforms for nonequispaced data, ii. Applied and Computational Harmonic Analysis, 2(1), pp. 85-100, 1995. DOI: 10.1006/acha.1995.1007.
[22] Tanton, J., Encyclopedia of Mathematics. New York: Facts on File, 2005.
[23] Abramowitz, M. and Stegun, I., Handbook of mathematical functions with formulas, graphs, and mathematical tables, 10th printing. Washington, D.C.: Dover, 1972. DOI: 10.1063/1.3047921.
[24] Gilbert, A.C., Li, Y., Porat, E. and Strauss, M.J., Approximate sparse recovery: Optimizing time and measurements, Proceedings of the 42nd ACM symposium on Theory of computing, pp. 475-484, 2010. DOI: 10.1145/1806689.1806755.
A. López-Parrado, completed his BSc. Eng. in Electronics Engineering in 2002 at Universidad del Quindío, Armenia, Colombia, and his MSc. degree in Electronics in 2009 at Universidad del Valle, Cali, Colombia. He is currently a PhD. candidate in Electrical and Electronics Engineering at Universidad del Valle, Cali, Colombia. His research interests are the FPGA design of complex digital systems, design of baseband processors, DSP complex functions, embedded systems, and compressive sensing. He is an assistant professor in the Electronics Engineering Program at Universidad del Quindío, Colombia. ORCID: 0000-0002-0274-6901
J. Velasco-Medina, completed his BSc. Eng. in Electrical Engineering in 1985 at Universidad del Valle, Cali, Colombia, his MSc. degree in Microelectronics 1995 at Universite De Grenoble I (Scientifique Et Medicale - Joseph Fourier), and his PhD. degree in Microelectronics in 1999 at Institut National Polytechnique De Grenoble, France. His research interests are the FPGA design of complex digital systems, design of baseband processors, Cryptosystems, DSP complex functions, DNA processor, bionanomachines, bionanosensors, biological systems modeling, and Citocomputation. He is a titular professor in the Electrical and Electronics Engineering School of Universidad del Valle, Cali, Colombia. ORCID: 0000-0003-4091-1055