
DOI: https://doi.org/10.15446/dyna.v83n198.49930
New robust capability ratios approaches for quality control
Nueva propuesta de índices de capacidad robustos para el control de la calidad
Salvador Naya a, Andrés Devia-Rivera b, Javier Tarrío-Saavedra a & Miguel Flores c
a Escuela Politécnica Superior, Departamento de Matemáticas. Grupo
MODES, Universidad de A Coruña, España. salva@udc.es, jtarrio@udc.es
b Departamento de Marketing Comercial, Avon
Cosmetics S.A.U., Madrid, España. andres.devia@avon.com
c Facultad de Ciencias, Departamento de Matemáticas. Escuela
Politécnica Nacional, Quito, Ecuador. miguel.flores@epn.edu.ec
Received: April 1rd, 2015. Received in revised form: November 20th, 2015. Accepted: March 30th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Robustness of process capability
measurements is a very important matter in statistical quality control. In this
paper, two new classes of capability measurements are studied as robust
mechanisms to detect the influence of factors that may cause large departures
from the process' engineering specifications. The behavior of the new indices
was analyzed by comparing their performance to other capability measures that
have been widely studied in literature. The paper aims to investigate the
robustness of the new capability ratios under the presence of outliers and a
lack of normality. For this purpose, bootstrap techniques were applied to
detect the true potential capability of a process via statistical inference
methods. The accuracies of the proposed indices are discussed by means of
numerical results from a real data example.
Keywords: Process capability ratio, robust statistics, bootstrap hypothesis testing, bootstrap confidence intervals.
Resumen
En este
trabajo, se proponen dos nuevos índices de capacidad robustos para detectar la
influencia de los factores que pueden causar grandes desviaciones de las
especificaciones técnicas del proceso. El comportamiento de estos nuevos
índices se analizó mediante la comparación de su rendimiento con respecto a
otras medidas de capacidad ampliamente estudiados en la literatura. El trabajo
tiene como objetivo investigar la robustez de estos nuevos índices de capacidad
bajo la presencia de valores extremos y de falta de normalidad. Para este
propósito, se aplicaron técnicas de remuestreo Bootstrap para detectar la
verdadera capacidad potencial de un proceso a través de los métodos de
inferencia estadística. La precisión de los índices propuestos es discutida por
medio de resultados numéricos con un ejemplo de datos reales.
Palabras clave: índices de capacidad; estadística robusta, contraste de hipótesis bootstrap, intervalos de confianza bootstrap.
1. Introduction
A process capability ratio (PCR) is a numerical score that helps the manufacturers to know whether the output of a process meets the engineering specifications. Large values of the ratio indicate that the current process is capable of producing items that meet or exceed customer requirements. Unfortunately, traditional assumptions of the data, such as normality or independence are often violated in many real situations. A common scenario, in which the assumptions of normality or independent and identically distributed data (i.i.d.) does not hold, is, for example, when the data are autocorrelated or when they belong to non-centered and skewed distributions. Specifically, if the assumption of normality is violated, it could then be very difficult, or even impossible, to obtain closed expressions for the probability distribution of the PCR estimator. This means that, in many cases, it is not possible to derive exact confidence intervals for the estimates of process capability. As a consequence of this, capability estimates may be far away from the true parameters of interest, and manufacturers could, therefore, be making the wrong decisions about the quality management of the process.
Many authors have studied different estimators for process capability under various distributional settings. Recent advances in inferential analysis applied to quality control techniques have motivated more theoretical research into the distribution theory of estimated PCR (see, for instance, the works by Chou and Owen [1], Clements [2], Pearn et al. [3], Ebadi and Shahriari [4], Kotz and Johnson [5], and Chien-Wei et al. [6]). The last two presented an exhaustive discussion on a number of capability indices, their sampling properties and practical applications. Moreover, there are some studies that address capacity indexes applied to autocorrelated data, such as Pan et al.'s [7] work that is applied to environmental features. Additionally, in terms of the particular case that deals with non-normal data and processes with unilateral specifications, extensive discussions can be found in the work undertaken by the following authors: Somerville and Montgomery [8], Kotz and Lovelace [9], Shore [10], Tang and Than [11], Chang et al. [12], Pearn and Chen [13], and Kotz and Johnson [14]. Most of the literature devoted to the study of process capability analysis frequently considers four indices, Cp, Cpk, Cpm, Cpmk, which are defined as:

Where USL and LSL are the upper and the lower
specification limits for the variations in the process,  is the process mean,
is the process mean, 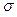 is the process
standard deviation,
is the process
standard deviation, 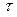 is some target value of interest in
the process, d is the half of the spread between the upper and lower
engineering specifications, and m is the midpoint between the
specification limits.
is some target value of interest in
the process, d is the half of the spread between the upper and lower
engineering specifications, and m is the midpoint between the
specification limits.
It is well known that indices Cp and Cpm are improved when the process data comes from symmetric distributions, e.g. the normal one. These are used to estimate process capability when two-sided tolerance limits are of concern. In the case of one-sided specifications, capability indices Cpk and Cpmkare preferred to obtain the desired process capability estimates [15, 16]. The Cpmk index deals with the departure of the process mean m from the target value t. It does this faster than the indices, Cp, Cpk and Cpm while remaining sensitive to changes in the total deviation of the process (see the expression in equation (4)). A handicap of most capability measures is related to their efficiency, which strongly depends on the appropriate estimation of the process variability. They are also influenced by the shape of the underlying distribution function that characterizes it (see, for instance, the papers by Heavlin [17], Chou and Owen [1], Pearn et al. [3] and Borges and Ho [18] for a more theoretical discussion).
The present paper is concerned with the estimation of process capability measurement when the data are possibly affected by contamination, hereafter the outliers, which may be an alert from an out-of-control process. A real data example is presented to compare the performance of the new capability ratios relative to the standard indices (1) to (4), that are under various schemes of distributions, sample sizes, and percentages of contamination of data.
The analysis consisted of a double inferential procedure. Bootstrap techniques for statistical inference were used to study the degree of potential capability of processes generated by distributions that have been affected by different outliers in different percentages. Bootstrap techniques for statistical inferences were used to study the degree of potential capability of processes that were generated by distributions affected by the different percentage of outliers. Inferential methods consisted of testing a standard null hypothesis in the context of process capability analysis. Moreover, approximately 95 percent bootstrap confidence intervals were obtained for the indices.
The present study is organized as follows: in section 2, definitions and mathematical formulations to compute the new capability indices are given. In section 3, theoretical basis of the bootstrap approach for statistical inference are introduced in a process capability analysis context. Section 4 is devoted to results obtained by applying the indices and methods described in section 3. Finally, numerical results and concluding remarks are discussed in section 5.
2. Robust process capability ratios
2.1. Robust capability measures for quality process
In a broad, but non theoretical sense, since outliers are data that commonly come from distributions different from the main set of data, it could be thought that the presence of outliers could be evidence that the process is out of statistical control. In that sense, there are a wide range of mathematical methods to deal with the problem of outliers. All these methods are connected to robust statistics [19]. Robust statistics are used in many applications of statistical process control analysis. Abu-Shawiesh and Abdullah [20] studied control limits for control charts by using robust estimates of process parameters (location, scale, shape, etc.). In Grznar et al.'s paper [21], the authors present a routine for outlier detection based on the smoothing methods. Kocherlakota and Kocherlakota [22] discuss different methods to obtain confidence intervals for PCR based on robust estimates under non normal data. Prasad and Bramorski [23] studied the interactions between outliers and correlation structures as unknown sources of variability under the scope of time series. Also, Yeh and Bhattacharya [24] proposed an index based on the idea of estimating non-conforming proportions. They also discussed a methodology to obtain bootstrap confidence intervals.
In the following subsections, an ordered
sample of n independent identically distributed (i.i.d.) random variables
(r.v.) with the same distribution of the process X is represented by  , and a corresponding realization of n items taken from X is
denoted by
, and a corresponding realization of n items taken from X is
denoted by  . Some robust estimators that will be used in the rest of this paper
are the standard deviation,
. Some robust estimators that will be used in the rest of this paper
are the standard deviation,  , the sample range,
, the sample range, 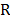 , the median,
, the median,  , and the first and third quantiles,
, and the first and third quantiles,  and
and  .
.
2.2. Definition of Cpk and Cprk indices
The introduction of these new process capability estimates is justified since there are systems characterized by the existence of sources of deviations that make large departures from the engineering specifications. We assume that such sources of deviations take place due to the presence of outliers in the data.
The first class of ratio that we introduce, Cpr, is based on the idea of the outlier detection criteria that is defined by the boxplot charts. It is expected that Cpr will be robust for detecting outliers when it is used to estimate the process capability of two-sided specifications systems. The second class of ratio, denoted by Cprk, was developed to estimate process capability for unilateral (one-sided) specifications in a similar way to that of the equations (2) and (4). Cpr measure the potential process capability while Cprk estimate the real capability of a process.
We define the new indices Cpr and Cprk as:
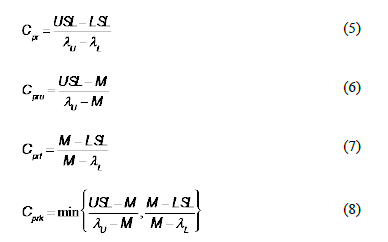
We stress that 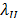 and
and  are, respectively, two robust
measures for the upper and the lower bounds of an in-control process, defined
as:
are, respectively, two robust
measures for the upper and the lower bounds of an in-control process, defined
as:
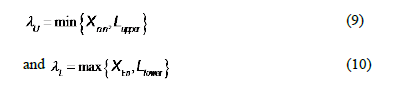
Where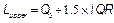 ,
, 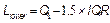 and
and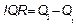 is the sample interquartile range. Thus, the quantity
is the sample interquartile range. Thus, the quantity 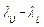 represents a new
robust measure for the process width.
represents a new
robust measure for the process width.
Fig. 1 shows a basic representation of a
univariate process distribution based on the idea of box-plot charts, i.e. based on a robust definition for outliers
into the data set. Thus, if we denote the domain of the process by  , then any point
belonging to
, then any point
belonging to  , where
, where  is defined as the set
is defined as the set 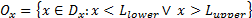 ,
will represent an outlier for the process X. Let us analyze situations
represented in A, B or C, and A' , B' or C'. Under the new approach, three
elemental criteria can be used to construct process capability measures based
on the (natural) process variability estimation. The setting can be defined as
follows:
,
will represent an outlier for the process X. Let us analyze situations
represented in A, B or C, and A' , B' or C'. Under the new approach, three
elemental criteria can be used to construct process capability measures based
on the (natural) process variability estimation. The setting can be defined as
follows:
i) For bilateral specifications, the process width is estimated by:

ii) For one upper specification, the process width is estimated by:

iii) For one lower specification, the process width is estimated by:
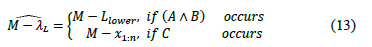
3. Bootstrap analysis
3.1. Bootstrap based inference methods
In recent
years, due to the analytical advances in industry control, not only point
estimation but also hypothesis testing and interval estimation, is often
obligatory for the producer to demonstrate process capability as part of the
contract. In that sense, an important part of the analysis included in the
present paper is based on the behavior results of hypothesis testing and
confidence intervals for the indices and 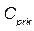 , relative to the indices (1) to (4), that are obtained
via bootstrap techniques. Informally, bootstrap methods are based on sampling
with replacement following the next idea. Let
, relative to the indices (1) to (4), that are obtained
via bootstrap techniques. Informally, bootstrap methods are based on sampling
with replacement following the next idea. Let 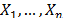 , a sequence of n i.i.d.
r.v. with the same distribution of the process X, and
, a sequence of n i.i.d.
r.v. with the same distribution of the process X, and 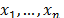 a realization of size n;
then a uniformly distributed random variable
a realization of size n;
then a uniformly distributed random variable  taking values on the set
taking values on the set 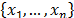 is defined by the probability
distribution
is defined by the probability
distribution
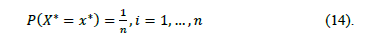
Thus, a bootstrap sample, denoted by 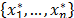 , is a sample drawn with replacement from the original sample
, is a sample drawn with replacement from the original sample 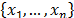 by using the law of
probability distribution defined in (14). In the next sections we describe the
methods used in this paper in the context of statistical inference for PCR.
by using the law of
probability distribution defined in (14). In the next sections we describe the
methods used in this paper in the context of statistical inference for PCR.
3.2. Hypothesis testing
From industry
experience, it is frequently necessary to demonstrate that the capability ratio 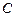 meets or exceeds a
particular target value, say
meets or exceeds a
particular target value, say  . This may be formulated as a hypothesis testing problem,
i.e.
. This may be formulated as a hypothesis testing problem,
i.e. 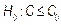 (Process is not
capable) and
(Process is not
capable) and  (Process is
potentially capable). We would like to test
(Process is
potentially capable). We would like to test 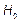 against
against  in the case of the
indices
in the case of the
indices  and
and 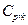 relative to the indices (1)
to (4), in different scenarios. Several authors have investigated this test
(see for instance Kane [25], Montgomery [26], Lin and Pearn [27], Shu and Lu
[28], Mathew et al. [29] and Albing [30]). In all mentioned works, the authors
have dealt with this problem by finding parametric distributions for test
statistics under the null hypothesis. Regarding the above, we have avoided
complicated mathematical processes to derive the null distribution of any
pivotal test statistic based on the
relative to the indices (1)
to (4), in different scenarios. Several authors have investigated this test
(see for instance Kane [25], Montgomery [26], Lin and Pearn [27], Shu and Lu
[28], Mathew et al. [29] and Albing [30]). In all mentioned works, the authors
have dealt with this problem by finding parametric distributions for test
statistics under the null hypothesis. Regarding the above, we have avoided
complicated mathematical processes to derive the null distribution of any
pivotal test statistic based on the  and
and 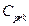 indices. Thus, we have proposed a reasonable
alternative based on bootstrap techniques to test the null hypothesis
indices. Thus, we have proposed a reasonable
alternative based on bootstrap techniques to test the null hypothesis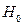 . The approach implemented in this paper is based on the ideas
discussed by Hall and Wilson [31] and Becher et al. [32]. The method is defined
as follows.
. The approach implemented in this paper is based on the ideas
discussed by Hall and Wilson [31] and Becher et al. [32]. The method is defined
as follows.
Let us denote 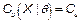 as the value of the
process capability ratio of the process X,
with
as the value of the
process capability ratio of the process X,
with 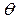 representing a
non-stochastic set of intrinsic parameters of the quality process X, and u representing one of the following classes of indices:
representing a
non-stochastic set of intrinsic parameters of the quality process X, and u representing one of the following classes of indices: 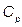 ,
,  ,
, 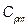 ,
, 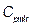 ,
, 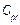 and
and 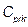 . In what follows, we shall consider that
. In what follows, we shall consider that 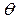 contains
(non-identical) subsets of intrinsic parameters such as:
contains
(non-identical) subsets of intrinsic parameters such as: 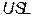 ,
,  ,
,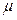 ,
,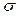 ,
,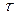 ,
, ,
,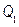 ,
, ,
,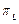 , and
, and 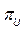 , where
, where 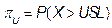 , and
, and 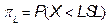 are the upper and
lower proportions of non-conformity detected in the process, respectively. The
corresponding sample estimator and bootstrap estimator of the index
are the upper and
lower proportions of non-conformity detected in the process, respectively. The
corresponding sample estimator and bootstrap estimator of the index 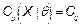 are
are 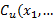 ,
, and
and  , where sub index b represents the b-th bootstrap
replicate
, where sub index b represents the b-th bootstrap
replicate 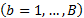 .
.
The study of the probability distribution
of the estimator  is equivalent to finding the
distribution of the inverse of a random variable. As it can be seen from the
equations (11) to (13), this random variable contains a highly nonlinear
transformation of order statistics. To solve this problem, long and
tedious algebra are necessary, as well
as the application of asymptotic results from the distribution theory of order
statistics. This is outside the scope of this paper and has been left to future
work.
is equivalent to finding the
distribution of the inverse of a random variable. As it can be seen from the
equations (11) to (13), this random variable contains a highly nonlinear
transformation of order statistics. To solve this problem, long and
tedious algebra are necessary, as well
as the application of asymptotic results from the distribution theory of order
statistics. This is outside the scope of this paper and has been left to future
work.
A common alternative to constructing
useful pivotal statistics, avoiding such a theoretical analysis, is based on
the idea of using bootstrap techniques. Hall and Wilson [31] proposed two
guidelines to test hypotheses for the population mean based on percentiles of
the null distribution of a bootstrap test statistic. Due to every u-th class of capability, ratio  is an univariate real-valued
function of the sample
is an univariate real-valued
function of the sample  . We can adapt the first guideline in the above mentioned paper to
test
. We can adapt the first guideline in the above mentioned paper to
test  against
against 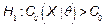 for a specific value
for a specific value  . The implementation of the test is synthesized as follows:
. The implementation of the test is synthesized as follows:
i) Null
statistic: Computing the ratio  with the original
sample
with the original
sample  , a natural null statistic
, a natural null statistic 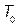 is given by
is given by
where 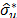 is a suitable estimator of
the squared root of
is a suitable estimator of
the squared root of . In the present work, we propose to use a large enough number B0 of bootstrap samples of
. In the present work, we propose to use a large enough number B0 of bootstrap samples of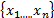 to compute
to compute

where  is the bootstrap estimator of
is the bootstrap estimator of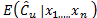 . It can be proved that
. It can be proved that 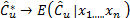 with probability one [31,33].
with probability one [31,33].
ii) Test statistic: The statistic 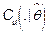 is computed with the b-th resample
is computed with the b-th resample 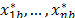 . Thus, the b-th bootstrap
test statistic is obtained by computing
. Thus, the b-th bootstrap
test statistic is obtained by computing

for 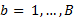 . Here,
. Here, 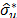 is the bootstrap estimator of the squared root
of
is the bootstrap estimator of the squared root
of 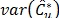 , which is obtained in the same way as
, which is obtained in the same way as

Informally,
the basic idea of the expression (17) is based on the assumption that the
distribution of the statistic 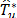 accurately mimics the
distribution of
accurately mimics the
distribution of 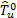 . Thus, the decision rule for the test at the b replication is to rejec
. Thus, the decision rule for the test at the b replication is to rejec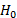 t if
t if 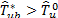 or not to reject
or not to reject 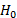 if
if 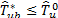 .
.
iii) P value: Se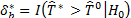 t, where the probability or p-value in the expression (17) is
computed by:
t, where the probability or p-value in the expression (17) is
computed by:

3.3. Confidence intervals
Bootstrap
methods to construct confidence intervals for PCR, have been widely studied by
several authors, e.g. Franklin and Wasserman [34,35], Choi et al. [36], Tong and Chen [37], Yeh
and Bhattacharya [24], Balamurali and Kalyanasundaram [38], Mathew et al. [29],
and Wang et al. [39] among others. The conventional parametric approach would
suggest that the probability distribution of capability ratios  and
and  , but due to the same reasons explained in section 3.2, from a
practical point of view, it makes more sense to try to approximate the
distribution of every class of ratio,
, but due to the same reasons explained in section 3.2, from a
practical point of view, it makes more sense to try to approximate the
distribution of every class of ratio, 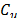 , via bootstrap techniques. In this paper, we have used the method
of bias corrected percentile bootstrap (BCPB). A complete justification of this
method is in Efron [40].
, via bootstrap techniques. In this paper, we have used the method
of bias corrected percentile bootstrap (BCPB). A complete justification of this
method is in Efron [40].
The method is
summarized as follows: firstly, using the ordered distribution of  ,
,
,
, , a significance level is fixed, a , and then the following quantities are calculated:
, a significance level is fixed, a , and then the following quantities are calculated: 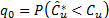 ,
, 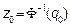 ,
, 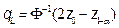
 , where
, where  is the inverse of the
standard normal probability distribution and
is the inverse of the
standard normal probability distribution and 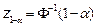 is the
is the 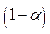 th-quantile of the standard normal distribution. Then, using
a large number
th-quantile of the standard normal distribution. Then, using
a large number  of bootstrap
resamples, a
of bootstrap
resamples, a  percent BCBP confidence interval for
percent BCBP confidence interval for 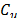 , is given by
, is given by 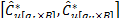 .
.
Efron and Tibshirani [41] indicated that a rough minimum of 1000 bootstrap samples is usually sufficient to compute reasonably accurate confidence interval estimates. Nevertheless, numerical results included in the present paper have been obtained by using B=10000 bootstrap samples.
4. Numerical results
The following subsections presents the results corresponding to the application of the proposed capability indices (and their quality assessment methodology) to the real data.
4.1. Real data example
For the purpose of investigating whether outliers can affect decisions in a quality management process, in this section we present numerical results obtained from the application of the new approach to a real data application.
Original experimental data were collected from a study of 150 test steel pipes, which were analyzed in the Science and Engineering of Materials labs at the University of A Coruña in Spain. Originally, the study consisted of developing statistical quality control measurements on traction-resistance by using the European norm UNE-EN 10002-140. Previous analyses of goodness of fit confirmed that the data were normally distributed with a 516 mean and standard deviation of 20 for 95% of confidence level. Fig. 2, shows a histogram describing the real data set.
Fig. 2 shows that the data are centered to its mean value. In this case, the sample mean is very close to the sample median, 516.3 and 517.6 respectively, and the sample standard deviation is 20.81. Moreover, the histogram also shows that the data set is a little skewed to the left: the skewness coefficient is -0.1641, whereas the kurtosis excess is 3.0112.
In terms of capability, several indices were computed to characterize the process X and for which the estimates of LSL and USL are 453.87 and 578.73 respectively. These values remained fixed during the whole bootstrap analysis and their results will be discussed in subsection 4.2.
For the first classical
approach, the estimate 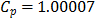 . This value tells us that the process
seems to be potentially possible under the 3s criteria. The other classical ratios showed little differences with respect to
the
. This value tells us that the process
seems to be potentially possible under the 3s criteria. The other classical ratios showed little differences with respect to
the 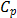 measure. In fact, the estimates were
measure. In fact, the estimates were 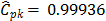 ,
, 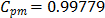 , and
, and 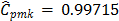 , which suggest that process is not
possible. In this case,
, which suggest that process is not
possible. In this case, 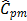 and
and  were computed by choosing the value
were computed by choosing the value 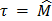 (target = median). Finally, the proposed
measures,
(target = median). Finally, the proposed
measures, 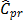 and
and  suggest the same conclusion: the
suggest the same conclusion: the  index, i.e., the process is potentially
possible, and
index, i.e., the process is potentially
possible, and  and
and  .
.
4.2. Bootstrap-based inference results
In this section, we present the results obtained by the bootstrap based statistical inference approach. The results collected in the following tables were obtained after varying the sample size and also the percentage of outliers in the original experimental data. After having applied the goodness of fit tests for contaminated data, we conclude that both 5 percent and 10 percent of outliers resulted in lack of normality for the original data. This fact added a third source of lack of robustness for all capability measures.
Table 1 shows results of the bootstrap hypothesis testing that was described in section 3.1. Firstly, allow us to draw your attention to the columns in Table 1. It can be seen that in case of normally distributed data (0% outliers), p-values seem to decrease as the sample size increases for all indices even though, as it was expected, p-values are less than the 0.05 nominal significance level. Thus, in this experiment, the tests do not fail by rejecting the null hypothesis.
When data
significantly departs from normality (5% and 10% outliers), some differences
can be observed in the performance behavior of indices 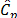 ,
,  and
and  , relative
to the indices
, relative
to the indices  ,
,  and
and 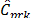 .
.
For a moderate level of contamination of
data (5% outliers), indices 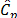 ,
,  do
not reject the null hypothesis. However, it seems that the test tends are not
rejected when sample size increase. For a higher level of outliers (10%
outliers), results show that all indices behave as expected and they gain in
robustness. In fact, this happens because they do not reject H0,no matter the sample size.
do
not reject the null hypothesis. However, it seems that the test tends are not
rejected when sample size increase. For a higher level of outliers (10%
outliers), results show that all indices behave as expected and they gain in
robustness. In fact, this happens because they do not reject H0,no matter the sample size.
Results for indices  ,
,  show
that these capability measures were more robust than the other indices. These
measurements do not fail by rejecting H0.
show
that these capability measures were more robust than the other indices. These
measurements do not fail by rejecting H0.
Finally, results concerning the proposed
indices  and
and 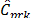 show some evidence
that the indices are robust capability measures. This is because these indices
do not reject the null hypothesis when data are completely out-of-control.
show some evidence
that the indices are robust capability measures. This is because these indices
do not reject the null hypothesis when data are completely out-of-control.
Table 2 shows results on approximately 95 percent confidence intervals obtained via the bias corrected percentile bootstrap method. It can be seen that some results are somewhat surprising, relative to the results collected in Table 1.
Firstly, for normal distributed data (0%
outliers), natural intuition tells us that confidence intervals should contain
the hypothetical value C0 = 1 when sample sizes increase. As it can be seen in Table 2, the results of
our experiment show that the proposed indices  and
and 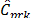 showed
the expected behavior when the sample size was greater than or equal to 300.
This result suggests that these two new classes of process capability
measurements have robust properties in normal conditions.
showed
the expected behavior when the sample size was greater than or equal to 300.
This result suggests that these two new classes of process capability
measurements have robust properties in normal conditions.
Nevertheless, when there are non-normal conditions (5% and 10% outliers), the 95% confidence intervals for the proposed indices are surprisingly unified (Cpr and Cprk lies within the confidence interval).
For both,
moderate and highly contaminated data (5% and 10% outliers), upper limits of
obtained confidence intervals tend to be less than 1 (Cp, Cpk, Cpm and Cpmk are out of the
interval). This fact allows to consider that classical measures  and
and  show a better behavior
when sample size increase (n >100).
show a better behavior
when sample size increase (n >100).
Finally, 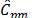 and
and 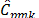 indices can be seen to be more conservative than the other indices,
no matter the sample size. These two measurements suggest that when data are
not normal the process is not possible.
indices can be seen to be more conservative than the other indices,
no matter the sample size. These two measurements suggest that when data are
not normal the process is not possible.
Taking the results into account, the proposed robust indices could be applied in a wide range of study cases, e.g. energy efficiency evaluation, academic evaluation, or the assessment of technology and innovation in companies [42-46].
5. Conclusions
In this paper, two classes of capability measurements inspired by the idea of robustness derived from the theory of construction box-plot charts have been studied. These new measurements were formulated by defining two new classes of robust process capability ratios that were then compared with traditional ratios in the literature, under several experimental schemes.
Due to the difficulty of obtaining the probability distribution of the new capability ratios, bootstrap methods were applied to study the robustness of the indices via the statistical inference approach. Thus, bootstrap hypothesis testing and bootstrap confidence intervals were used to test and estimate the true level of capability of a quality process.
The bootstrap experimental analysis was implemented by using a set of laboratory data that came from the analysis of the traction-resistance of steel pipes by using the European norm UNE-EN 10002-1 at the University of A Coruña, Spain.
The inference based results showed that the proposed capability measurements were comparable with the traditional process capability ratios. Comparative analyses suggested that the new ratios are robust measures to estimate the true level of process capability under normality. Moreover, the new capability ratios were shown to be less conservative than some traditional ratios under the presence of outliers; this produced a moderate lack of normality that seems to improve when increasing the sample size.
Acknowledgements
This research has been partially supported by the Spanish Ministry of Science and Innovation, Grant MTM2014-52876-R (ERDF included) and the Vicerrectorado de Investigación de la EPN (Ecuador).
References
[1] Chou, Y.M. and Owen, D.B., On the distribution of the estimated process capability indices. Communications in Statistics - Theory and Methods, 18, pp. 4549-4560, 1989. DOI: 10.1515/EQC.2003.5
[2] Clements, J.A., Process capability indices for non normal calculations. Quality Progress, 22, pp. 49-55, 1989. DOI: 10.1080/08982119408918772
[3] Pearn, W., Kotz, S. and Johnson, N.L., Distributional and inferential properties of process capability indices. Journal of Quality Technology, 24, pp. 216-231, 1992.
[4] Ebadi, M. and Shahriari, H., A process capability index for simple linear profile. The International Journal of Advanced Manufacturing Technology, 64, pp. 857-865, 2013. DOI: 10.1007/s00170-012-4066-7
[5] Kotz, S. and Johnson, N.L., Process Capability Indices. Chapman & Hall, London, 1993.
[6] Chien-Wei, W., Pearn, W.L. and Kotz, S., An overview of theory and practice on process capability indices for quality assurance. International Journal of Production Economics, 117, pp. 338-359, 2009. DOI: 10.1016/j.ijpe.2008.11.008
[7] Pan, J.N., Li, C.I. and Chen, F.Y., Evaluating environmental performance using new process capability indices for autocorrelated data. Environmental Monitoring and Assessment, 186, pp. 6369-6384, 2014. DOI: 10.1007/s10661-014-3861-z
[8] Somerville, S.E. and Montgomery, D.C., Process capability indices and non-normal distributions. Quality Engineering, 9, pp. 305-316, 1996. DOI: 10.1080/08982119608919047
[9] Kotz, S. and Lovelace, C.R., Introduction to Process Capability Indices: Theory and Practice. Arnold, London, 1998.
[10] Shore, H., A new approach to analysing non-normal quality data with applications to process capability analysis. International Journal of Production Research, 36, pp. 1917-1933, 1998. DOI: 10.1080/002075498193039
[11] Tang, L.C. and Than, S.E., Computing process capability indices for non normal data: A review and comparative study. Quality and Reliability Engineering International, 15, pp. 339-353, 1999. DOI: 10.1002/(SICI)1099-1638(199909/10)15:5<339::AID-QRE259>3.0.CO;2-A
[12] Chang, Y.S., Choi, I.S. and Bai, D.S., Quality and Reliability Engineering International, 18, pp. 383-393, 2002.
[13] Pearn, W.L. and Chen, K.S., One-sided capability indices Cpu and Cpl: decision making with sample information. International Journal of Quality and Reliability Management, 19, pp. 221-245, 2002. DOI: 10.1108/02656710210421544
[14] Kotz, S. and Johnson, N.L., Process capability indices -A review, 1992-2000 with discussion. Journal of Quality Technology, 34, pp. 2-53, 2002.
[15] Grau, D., New process capability indices for one-sided tolerances. Quality Technology & Quantitative Management, 6, pp. 107-124, 2009.
[16] Grau, D., Process yield, process centering and capability indices for one-sided tolerance processes. Quality Technology & Quantitative Management, 9, pp. 153-170, 2012.
[17] Heavlin, W.D., Statistical properties of capability indices. Technical Report 320. Technical Library, Advanced Micro Devices, Inc., Sunnyvale, CA, 1988.
[18] Borges, W. and Ho, L.L., A fraction defective based capability index. Quality and Reliability Engineering International, 17, pp. 447-458, 2001. DOI: 10.1002/qre.438
[19] Huber, P., Robust Statistics. John Wiley & Sons, New York, 1981. DOI: 10.1007/978-3-642-04898-2_594
[20] Abu-Shawiesh, M.O. and Abdullah, M.B., New robust statistical process control chart for location. Quality Engineering, 12, pp. 149-159, 1999. DOI: 10.1080/08982119908962572
[21] Grznar, J. and Booth, D.E., A robust smoothing approach to statistical process control. Journal of Chemical Information and Computer Sciences, 37, pp. 241-248, 1997. DOI: 10.1021/ci9600317
[22] Kocherlakota, S. and Kocherlakota, K., Confidence intervals for the process capability ratio based on robust estimators. Communications in Statistics - Theory and Methods, 23, pp. 257-276, 1994. DOI: 10.1080/03610929408831252
[23] Prasad, S. and Bramorski, T., Robust process capability indices. International Journal of Management Science, 26, pp. 425-435, 1998. DOI: 10.1016/S0305-0483(97)00075-3
[24] Yeh, A.B. and Bhattacharya, S., A robust process capability index. Communications in Statistics - Simulation and Computation, 27, pp. 565-589, 1998. DOI: 10.1080/03610919808813495
[25] Kane, V.E., Process capability indices. Journal of Quality Technology, 18, pp. 41-52, 1986.
[26] Montgomery, D.C., Introduction to Statistical Quality Control, 6th edition. John Wiley & Sons, New York, 2009. DOI: 10.1002/qre.4680070316
[27] Lin, P.C. and Pearn, W.L., Testing process capability for one-sided specification limit with application to the voltage level translator. Microelectronics Reliability, 42, pp. 1975-1983, 2002. DOI: 10.1016/S0026-2714(02)00103-8
[28] Shu, M.H., Lu, K.H., Hsu, B.M. and Lou, K.R., Testing quality assurance using process capability indices CPU and CPL based on several groups of samples with unequal sizes. Information and Management Sciences, 17, pp. 47-65, 2006.
[29] Mathew, T., Sebastian, G. and Kurian, K.M., Generalized confidence intervals for process capability indices. Quality and Reliability Engineering International, 23, pp. 471-481, 2007. DOI: 10.1002/qre.828
[30] Albing, M., Process capability indices for Weibull distributions and upper specification limits. Quality and Reliability Engineering International, 25, pp. 317-334, 2009. DOI: 10.1002/qre.972
[31] Hall, P. and Wilson, S.R., Two guidelines for bootstrap hypothesis testing. Biometrics, 47, pp. 757-762, 1991. DOI: 10.2307/2532163
[32] Becher, H., Hall. P. and Wilson, S.R., Bootstrap hypothesis testing procedures. Biometrics, 49, pp. 1268-1272, 1993. DOI: 10.2307/2532271
[33] Hall, P., The Bootstrap and Edgeworth Expansion. Springer, NewYork, 1992. DOI: 10.1007/978-1-4612-4384-7
[34] Franklin, L.A. and Wasserman, G., Bootstrap confidence intervals of Cpk: An introduction. Communications in Statistics - Simulation and Computation, 20, pp. 231-242, 1991. DOI: 10.1080/03610919108812950
[35] Franklin, LA. And Wasserman, G., Bootstrap lower confidence limits for process capability indices. Journal of Quality Technology, 24, pp. 196-210, 1992. DOI: 10.1108/02656710210442875
[36] Choi, K.C., Nam, K.H. and Park, D.H., Estimation of capability index based on bootstrap method. Microelectronic Reliability, 36, pp. 1141-1153, 1996. DOI: 10.1016/0026-2714(95)00211-1
[37] Tong, L.I. and Chen, J.P., Lower confidence limits of process capability indices for nonnormal process distributions. International Journal of Quality Reliability Management, 15, pp. 907-919, 1998. DOI: 10.1108/02656719810199006
[38] Balamurali, S. and Kalyanasundaram, M., Bootstrap lower confidence limits for the process capability indices Cp, Cpk, and Cpm. International Journal of Quality & Reliability Management, 19, pp. 1088-1097, 2002. DOI: 10.1108/02656710210442875
[39] Wang, D.S., Koo, T.Y. and Chou, C.Y., On the bootstrap confidence intervals of the capability index Cpk for multiple process streams. International Journal for Computer-Aided Engineering and Software, 24, pp. 473-485, 2007. DOI: 10.1108/02644400710755870
[40] Efron, B., The Jackknife, the Bootstrap and other Resampling Plans. Society for Industrial and Applied Mathematics, Pennsylvania, 1982.
[41] Efron, B. and Tibshirani, R.J., Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statistical Science, 1, pp. 54-77, 1986. DOI: 10.1214/ss/1177013815
[42] Torres, L.M., Castellanos, Ó.F. and Fúquene, A.M., Evaluating Colombian SMEs technological innovation: Part 1: Conceptual basis, evaluation methodology and characterisation of innovative companies. Ingeniería e Investigación, 27(1), pp. 158-167, 2007.
[43] Jiménez, C., Cristancho, A. and Castellanos, O., The role of capability in technology valuation. Ingeniería e Investigación, 31(2), pp. 112-123, 2011.
[44] Cortés, H., Gallego, L. and Rodríguez, G., The engineering faculty today: An approach towards consolidating academic indicators. Ingeniería e Investigación, 31, pp. 74-90, 2011.
[45] Zaragoza-Fernández, S., Tarrío-Saavedra, J., Naya, S., López-Beceiro, J. and Álvarez-García, A., Impact estimates of the actions for the rehabilitation of energy efficiency in residential building. DYNA, 81(186), pp. 200-207, 2014. DOI: 10.15446/dyna.v81n186.39930
[46] Castrillón, R.D.P., González, A.J. and Ciro-Quispe, E., Energy efficiency improvement in the cement industry by wet process through integral energy management system implementation. DYNA, 80(177), pp. 115-123, 2013.
S. Naya, is professor in statistics at the University of A Coruña, Spain. He received a BSc. and MSc. in Mathematics from the University of Santiago de Compostela, Spain and a PhD in Industrial Engineering from the University of A Coruña, Spain with a with a Cum Laude mention of excellence. His main scientific-technical fields of interest are Statistical Quality Control, Reliability and Statistical Applications in Materials Engineering. He is an Elected Member of the ISI (International Statistical Institute) and was given the International Educator Award in 2013 from the Juarez Lincoln Martí Project. Currently he is Vice rector for Science Policy, Research and Transfer at the University of A Coruña. ORCID: 0000-0003-4931-9859.
A. Devia-Rivera, is an Excess and Obsolescence Planner at the Commercial Marketing Department of Avon Cosmetics in Madrid, Spain. He is a Statistical Engineer graduate from the University of Santiago de Chile, Chile. In 2008 he received a Diploma of Advanced Studies in Statistics and Operations Research from the University of A Coruña, Spain. He obtained his PhD in Statistics and Operations Research in January 2016 with a Cum Laude mention of excellence. His main scientific fields of interest are Statistical Modeling in Finance and Engineering. He has taught several courses in statistics, probability and time series as assistant professor in Chile, and he has published papers and short communications in the field of Statistical Modeling of Credit Risk. ORCID: 0000-0002-6499-5233
J. Tarrío-Saavedra, is an Industrial Engineer, has a MSc. and PhD in Statistics and Operations Research from the University of A Coruña (UDC). He was given a special PhD award in the area of Mathematics and Computer Science. Currently he is a Professor in Statistics, Statistical Quality Control, and Thermomechanical Fatigue on undergraduate and Master's degrees in the UDC. He has participated in 14 projects and research contracts with public and private entities. He is author of 34 scientific articles, 4 book chapters and 60 conference papers related to statistics, materials science, engineering and bibliometrics. He has conducted research at the University Paris Diderot - Paris 7. ORCID ID: 0000-0002-9584-127X
M.A. Flores, is a professor at the National Polytechnic School and a researcher at the Center for Modeling Mathematics at the National Polytechnic School in Quito, Ecuador. He is a BSc. in Statistical Computing Engineer from the Polytechnic School of the Coast. In 2006 he received a in MSc. in Operations Research from the National Polytechnic School, and in 2013 received a MSc. in Technical Statistics from the University of A Coruña. He is currently a doctoral student at the University of A Coruña in the area of Statistics and Operations Research. He has over 14 years professional experience in various areas of Statistics, Computing and Optimization, multivariate data analysis, econometric, Market Research, Quality Control, definition and construction of systems indicators, development of applications and optimization modeling. ORCID ID: 0000-0002-7742-1247