DOI: https://doi.org/10.15446/dyna.v82n191.51143

Intuitionistic fuzzy MOORA for supplier selection

MOORA versión difuso intuicionista para la selección de proveedores

 

Luis Pérez-Domínguez a, Alejandro Alvarado-Iniesta b, Iván Rodríguez-Borbón c & Osslan Vergara-Villegas d

 

a Department of Industrial and Manufacturing Engineering, Autonomous University of Ciudad Juarez, Juarez, México. luis.dominguez@uacj.mx
b Department of Industrial and Manufacturing Engineering, Autonomous University of Ciudad Juarez, Juarez, México. alejandro.alvarado@uacj.mx
c Department of Industrial and Manufacturing Engineering, Autonomous University of Ciudad Juarez, Juarez, México. ivan.rodriguez@uacj.mx
d Department of Mechatronics Engineering, Autonomous University of Ciudad Juarez, Juarez, México. overgara@uacj.mx

 

Received: January 28th, 2015. Received in revised form: March 26th, 2015. Accepted: April 30th, 2015

 

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The supplier selection is a critical activity within the administration of the supply chain. It is considered a complex problem given that it involves different aspects such as the alternatives to evaluate, the multiple criteria involved as well as the group of decision makers with different opinions. In this sense, the literature reports several methods to help in this difficult activity of selecting the best supplier. However, there are still some gaps in these methods; therefore, it is imperative to further develop research. Thus, the purpose of this paper is to report a hybrid method between MOORA and intuitionistic fuzzy sets for the selection of suppliers with a focus on multi-criteria and multi-group environment. The importance of decision makers, criteria and alternatives are evaluated in terms of intuitionistic fuzzy sets. Then, MOORA is used in order to determine the best supplier. An experimental case is developed in order to explain the proposed method in detail and to demonstrate its practicality and effectiveness.

Keywords: MCDM; MOORA; Intuitionistic fuzzy set; Supplier Selection.

Resumen
La selección de proveedores es una actividad crítica dentro de la administración de una cadena de suministro. Es considerado un problema complejo dado que involucra diferentes aspectos como son las mismas alternativas a evaluar, los múltiples criterios en consideración, así como el grupo de decisores con opiniones diferentes. En este sentido, la literatura reporta diversos métodos para ayudar en esta difícil actividad de seleccionar el mejor proveedor. Sin embargo, aún existen algunas brechas en dichos métodos por lo que resulta necesario seguir desarrollando investigación. Por lo tanto, el propósito del presente artículo es reportar un nuevo método basado en la hibridación de la técnica MOORA con conjuntos difusos intuicionistas para la selección de proveedores, con un enfoque de decisión multi-criterio y multi-grupal. La importancia de los decisores y criterios así como las alternativas se evalúan en términos de conjuntos difusos intuicionistas, posteriormente MOORA es usado para determinar la mejor alternativa. Un caso experimental es desarrollado con el fin de explicar el método propuesto de manera detallada y para demostrar su viabilidad y eficacia.

Palabras clave: MCDM; MOORA; Conjuntos difusos intuicionistas; Selección de Proveedores.

 

1. Introduction

Nowadays, market demands have motivated the industries to provide a fast and reliable service in order to meet customer requests that are sensitive in their requirements [1,2]. In this sense, supply chain management has fostered great interest in terms of company strategies to stay in global business. The works presented by [3- 5] claim that an important key issue for the administration of the supply chain is the correct selection of suppliers. [6,7] mention that the selection of suppliers is considered a multi-criteria problem in the field of decision-making. Additionally, the work of [8] argues that effective supplier selection is significant because it helps reduce operational costs. According to [9], the selection of the best supplier is a competitive advantage that can help to increase productivity and efficiency for any organization.

Hence, given the importance of selecting the best supplier, there are several multi-criteria methodologies that seek to provide support in the difficult task of making this decision. Such methodologies are being used by purchasing managers of companies, and even by top managers. Some of the most frequently reported methodologies in the literature are: artificial neural networks (1943, ANN), fuzzy sets (1965, FS), quality function deployment (1966, QFD), elimination and choice expressing reality (1968, ELECTRE), design of decision support systems (1971, DSS), simple multi-attribute rating technique (1971, SMART), genetic algorithm (1975, GA), data envelopment analysis (1978, DEA), analytic hierarchy process (1980, AHP), technique for order of preference by similarity to ideal solution (1981, TOPSIS), viseKriterijumsa optimizacija i kompromisno resenje (1998, VIKOR), dimensional analysis (1993, DA), analytic network process (1996, ANP), multi-objective optimization by ratio analysis (2006, MOORA), preference selection index (PSI, 2010), among several others [10-24]. We can therefore infer that the issue of decision-making has been investigated for many years and, as a result, several methodologies have been developed as support tools [25].

[26,27] report a classification of these methodologies within two groups: individual and hybrid. The first group is made up by AHP, TOPSIS, DEA, DSS, VIKOR, ELECTRE, MOORA, SMART, DA, MOORA, FS, ANN, GA, among many more. The second group is represented by AHP-TOPSIS, TOPSIS-VIKOR, DS-AHP, FDEMATEL, FVIKOR, FELECTRE, FAHP, AHP-GA, AHP-ANN, FTOPSIS, DEA-AHP, IFTOPSIS, IFAHP, among others. The literature reviewed shows that AHP and TOPSIS are two of the most frequently reported methodologies especially in the task of supplier selection [25,28,29]. Furthermore, it can be observed that the most frequently reported hybrids contain these methodologies along with fuzzy sets [3,6,30-33]. However, these methodologies by themselves as well as the hybrids with fuzzy sets present some deficiencies.

First, the AHP method requires decision makers (DMs) to utilize perception capabilities to undertake pair-wise comparisons, but AHP lacks the ability to reflect the way humans think. In other words, AHP uses crisp values to represent the subjective opinion from DMs, which is hard to estimate by exact numerical values [7,31-35]. Even though the fuzzy AHP method handles the fuzziness in the experts' subjective judgment with the aid of fuzzy set theory, the mathematical foundation is rather poor; for example, in terms of the conditions of reciprocity and transitivity, particularly where, is not equal to . Besides, defining the fuzzy Eigen-values tends to be complex [2, 36-38].

Second, TOPSIS deals with Euclidean distance [39, 40]. Euclidean distance assumes that criteria in evaluation are independent, which is sometimes not the case [41]. The same issue remains in the fuzzy version. As a result, there exists the opportunity to further develop research in the field of decision making in order to counteract weaknesses that can lead to making a wrong decision.

Recent papers show that multi-criteria methods are being used in combination with intuitionistic fuzzy sets (IFS). Particularly, IFS, proposed by Atanassov (1986), are a generalization of the classical fuzzy sets reported by Zadeh (1965). A literature review shows that over the past few years, the use of IFS in multi-criteria decision making (MCDM) has increased significantly [42-57]. IFS are more capable than traditional fuzzy sets at handling vague and uncertain information in practice [55-57].

Hence, the aim of this work is to present the hybrid of the MOORA (Multi-Objective Optimization on the basis of Ratio Analysis) method with IFS as an alternative methodology for MCDM.

The rest of this paper is organized as follows. Section 2 briefly presents the concepts related to IFS. Section 3 presents the description of MOORA. Section 4 describes the method proposed in this paper. In Section 5 a numerical case is presented in order to explain the proposed methodology. Finally, the conclusions and further works are presented in section 6.

 

2. Intuitionistic Fuzzy Set

A fuzzy set in is given by . Where is the membership function of the fuzzy set ; is the membership of in .

According to [58] an IFS is proposed by means of two functions expressing the degree of membership and non-membership of an element to the set . An IFS in is defined as . Where; . With the condition

The numbers denote respectively the degree of membership and degree of non-membership of element to the set .

The number is called the intuitionistic index of in . It is a measure of the degree of hesitancy of element in set . It should be noted that for each .

Hence, an IFS in is fully defined with the form . Where ; and . Different relations and operations are introduced over the IFSs [59] some of them are shown in eq. (1) and (2).

 

3. MOORA

Multi-Objective Optimization on the basis of Ratio Analysis (MOORA) was introduced by Brauers and Zavadskas for first time in 2006 [60]. The basic idea of the MOORA method is to calculate the overall performance of each alternative as the difference between the sums of its normalized performances which belongs to cost and benefit criteria. Thus, the MOORA method can be expressed concisely using the five following steps:

Step 1. Determine the decision-making matrix. The method begins with the identification of available alternatives and criteria. Then, the decision-making matrix (DMM) is constructed, which contains rows that represent the alternatives in evaluation, and columns that represent criteria under evaluation ( quantitative criteria and qualitative criteria). In this way, according to [61], the MDF is computed using eq. (3).

where, represent the alternatives, for represents the entries of the alternative with respect to criterion .

Step 2. Calculate the normalized decision-making matrix.

It is possible that the evaluation attributes are expressed in different units or scales of measurement; thereby, normalization is carried out [60]. Where the Euclidean norm is obtained according to eq. (4) to the criterion .

Thus, the normalization of each entry in the MDF is undertaken according to eq. (5).

The results obtained using eq. (5) are dimensionless values that lack scale, which allows the operations between criteria to be additive [61,62].

Step 3. Calculate the weighted normalized decision-making matrix. Considering [63] the different importance of criteria, the weighted normalized ratings are calculated with eq.(6).

Step 4. Calculate the overall ratings of cost and benefit criteria for each alternative. The overall ratings of benefit criteria are calculated as the sum of weighted normalized ratings of benefit criteria using eq. (7).

where is associated with benefit criteria.

Similarly, the overall ratings of cost criteria are calculated with eq. (8).

where is associated with cost criteria.

Step 5 Compute the contribution of each alternative. The contribution of each alternative is obtained using eq. (9) proposed by [60].

where represents the contribution of each alternative, 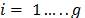are the maximum criteria and are the minimum criteria

Finally, the value can be positive or negative depending on the totals of its maxima (benefit criteria) and minima (cost criteria) in the decision matrix. An ordinal ranking of shows the final preferenc value.

 

4. Intuitionistic Fuzzy MOORA

Let be a set of alternatives and be a set of criteria to be evaluated. The Intuitionistic Fuzzy MOORA (IF-MOORA) procedure is described in the following steps:

Step 1. Constitute a group of Decision Makers and determine the importance of each one. Where is the set of decision makers (DMs). The importance of each DM is rated through a linguistic term expressed by intuitionistic fuzzy numbers. The linguistic terms and their corresponding intuitionistic fuzzy number (IFN) used for rating the weight of each one of the DMs are shown in Table 1.

Let be an intuitionistic fuzzy number for rating of kth DM. Then, the corresponding weight of kth DM is obtained using the concept proposed by [52]:

Step 2. Determine the importance of criteria. Normally, all criteria may not be assumed to be of equal importance, and DMs might give different opinions about the same criteria. Hence, all opinions need to be considered and combined into one. Linguistic terms shown in Table 1 are used to rate the importance of criteria by every DM.

Let be an intuitionistic fuzzy number assigned to criterion by the kth DM. Then, the weights of the criteria are computed using the IFWA operator proposed by [53]:

where and

Step 3. Construct the aggregated intuitionistic fuzzy decision matrix representing the rating of alternatives based on the opinions of decision makers.

Let be an intuitionistic fuzzy decision matrix (IFDM) of each DM. The linguistic terms used to evaluate each one of the alternatives according to the criteria are shown in Table 2.

All opinions of DMs need to be included into an aggregated intuitionistic fuzzy decision matrix (AIFDM). IFWA operator might be used.

Then, the AIFDM is defined as:

Specifically,

Step 4. Compute the aggregated weighted intuitionistic fuzzy decision matrix (AWIFDM). In this step, the AWIFDM is computed by considering the AIFDM, obtained in Step 3, and the vector of criteria weights, obtained in Step 2. The elements of AWIFDM are calculated using Eq. (1).

 

Step 5. Compute the sum of costs and benefits. In this step, the benefit (BN) and cost criteria (C) are identified. In this sense, the benefit criteria are the ones where maximum values are desired. On the other hand, cost criteria are where minimum values are preferred.

Thus, eq. (14) represents the sum of benefit criteria

where, are the benefit criteria for the alternative represent maximum criteria. Then, eq. (15) define the sum of the cost criteria.

where, represents the sum of the cost criteria for alternative are minimum criteria.

Step 6. Defuzzification of the sum of benefits and costs. In this step, the maximum and minimum criteria are defuzzified using the eq. (16) proposed by [54].

Step 7. Compute the contribution of each alternative. Calculate the contribution of each alternative

The value can be positive or negative depending on the totals of beneficial criteria and cost criteria in the decision matrix. An ordinal ranking of shows the final contribution of each alternative. Thus, the best alternative has the highest value, while the worst alternative has the lowest value.

Step 8. Rank the alternatives. Alternatives are sorted according to descending order of

 

5. Numerical Case

An assembly company dedicated to the production of submersible pumps has to assemble several components in its production line. In the process, there is a packing that unites two shells that maintain an electrical system running under water. A common failure of this packing is detected by a short circuit generated that disables the pump. In order to repair the pump, the packaging has to be removed to change it and replace the faulty electrical system.

Following pre-evaluation to identify potential suppliers of the packaging, five suppliers were found that could easily supply the material in the region where the assembly company is established. A group decision (GD) with two decision makers has been integrated. The GD has been determined to evaluate five suppliers for the new packing component. The procedure followed to choose the best supplier is shown below:

Four criteria are considered for representing the most significant features of the suppliers. Thus, the criteria considered are:

Five suppliers are considered for evaluation. Thus, the set of suppliers are denoted by.

Step 1. Constitute a group of DMs and determine the importance of each one. Two DMs constitute the group and their importance is shown in Table 3. Linguistic terms used for rating are shown in Table 1. In order to obtain the weight of each DM, eq. (10) was used, and for this case in particular all DMs have the same importance.

Step 2. Determine the importance of criteria. The evaluation of each DM about the importance of the criteria represented as linguistic terms is shown in Table 4.

Opinions of DMs are integrated by eq. (11) as follows:

Step 3. Construct the AIFDM representing the rating of alternatives based on the opinions of decision makers. The ratings given by every DM are given in Table 5. The AIFDM is obtained by eq. (12) and it is shown as follows,

Step 4. Compute the aggregated weighted intuitionistic fuzzy decision matrix. The AWIFDM is obtained using eq. (13).

Step 5. Compute the sum of benefits and costs. Service, Management and Technology are benefit criteria ; while Cost is a cost criteria . Table 6 shows the sum of benefit criteria for each alternative in evaluation is obtained using eq. (14).

Table 7 shows the sum of cost criteria for each alternative in evaluation calculated using eq. (15).

Step 6. Defuzzification of the sum of benefits and costs. The maximum (benefit criteria) and minimum criteria (cost criteria) are defuzzified by using eq. (16). The results are shown in the Table 8 and Table 9.

Step 7. Compute the contribution of each alternative . The contribution of each alternative is computed by using eq. (17). Table 10 shows the ratio for each alternative and its ranking.

Step 8. Rank the alternatives. The alternatives are ranked as . Then, alternative 1 is selected as the best supplier among the rest.

 

6. Conclusions

This paper presents a hybrid of MOORA and intuitionistic fuzzy sets for supplier selection. The method consists of eight steps and a numerical example was shown in order to illustrate it. The proposed methodology provides a robust hybrid technique that can assist decision makers in selecting the best alternative since IFS has the capability of handling subjective information that provides greater flexibility to solve problems in the field of decision-making.

As future work, it would be interesting to apply IF-MOORA in different areas where there are factors of decision-making regarding the selection of alternatives; for example, robot selection, personnel selection, projects selection, etc. Finally, it is suggested that comparisons are made with other methods and that the results be evaluated.

 

References

[1] Chou, S. and Chang, Y., A decision support system for supplier selection based on a strategy-aligned fuzzy SMART approach, Expert Systems with Applications, 34 (4), pp. 2241-2253, 2008. DOI: 10.1016/j.eswa.2007.03.001

[2] Arango, M., Adarme, W. and Zapata J., Collaborative inventory in supply chain optimization, DYNA, 80 (181), pp. 71-80, 2013.

[3] Deng, X., Hu, Y., Deng, Y. and Mahadevan, S., Expert systems with applications supplier selection using AHP methodology extended by D numbers. Expert Systems with Applications, 41 (1), pp. 156-167, 2014. DOI: 10.1016/j.eswa.2013.07.018

[4] Kannan, D., Beatriz, A., Sousa, L. De José, C. and Jabbour, C., Selecting green suppliers based on GSCM practices: Using fuzzy TOPSIS applied to a Brazilian electronics company. European Journal of Operational Research, 233, pp. 432-447, 2014. DOI: 10.1016/j.ejor.2013.07.023

[5] Avelar, L., García, J., Cedillo, G. and Adarme, W. Effects of regional infrastructure and offered services in the supply chains performance: Case Ciudad Juarez, DYNA, 81 (186), pp1-13, 2014

[6] Rouyendegh, B. and Saputro, T., Supplier selection using integrated fuzzy TOPSIS and MCGP: A Case Study, Procedia - Social and Behavioral Sciences, 116, pp. 3957-3970, 2014. DOI: 10.1016/j.sbspro.2014.01.874

[7] Lima, F., Osiro, L. and Carpinetti, L., A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection, Applied Soft Computing, 21, pp. 194-209, 2014. DOI: 10.1016/j.asoc.2014.03.014

[8] Dargi, A., Anjomshoae, A., Galankashi, M., Memari, A. and Tap, M., Supplier selection: A Fuzzy-ANP approach, Procedia - Computer Science, 31, pp. 691-700, 2014. DOI: 10.1016/j.procs.2014.05.317

[9] Khodadadzadeh, T. and Sadjadi, S., A state-of-art review on supplier selection problem, Decision Science Letters, 2 (2), pp. 59-70, 2013. DOI: 10.5267/j.dsl.2013.03.001

[10] McCulloch ,W.S. and Pitts W., A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biology, 5 (4), pp.115-133, 1943.

[11] Zadeh, L., Fuzzy set. Information and Control, 8, pp. 333-353, 1965. DOI: 10.1016/S0019-9958(65)90241-X

[12] Akao, Y., Development history of quality function deployment, The customer driven approach to quality planning and deployment. Minato, Tokyo 107 Japan: Asian Productivity Organization. 339 P., 1966.

[13] Roy, B., Classement et choix en présence de points de vue multiples (la méthode ELECTRE), La Revue d'Informatique et de Recherche Opérationelle (RIRO), 8, pp.57-75, 1968.

[14] Gorry, G. and Scott, M., A framework for management information systems, Sloan Management Review, 13, pp. 50 - 70, 1971.

[15] Holland, J., Adaptation in natural and artificial systems, University of Michigan Press, Ann Arbor, 1975.

[16] Charnes, A., Cooper, W. and Rhodes, E., Measuring efficiency of decision-making units, European Journal of Operational Research, 3, pp. 429-444, 1978. DOI: 10.1016/0377-2217(78)90138-8

[17] Saaty, T., The analytic hierarchy process, New York: McGraw-Hill, 1980.

[18] Hwang, C. and Yoon, K., Multiple attribute decision making: Methods and applications. New York: Springer-Verlag, 1981. DOI: 10.1007/978-3-642-48318-9

[19] Bahl, C. and Hunt, G., Decision-making theory and DSS design, ACM Sigmis Database, 15, pp.10-14, 1984. DOI: 10.1145/1017726.1017728

[20] Willis, T., Huston, C. and Pohlkamp F., Evaluation measures of just-in-time supplier performance, Production and Inventory Management Journal, 34 (2), pp. 1-5, 1993.

[21] Saaty, T., Decision making with dependence and feedback: The analytic network process, Pittsburgh, Pennsylvania: RWS Publications, 1996.

[22] Opricovic, S., Multicriteria optimization in civil engineering, Belgrade, Faculty of Civil Engineering, (in Serbian), 302 P., 1998.

[23] Brauers, W. and Zavadskas, E. ,The MOORA method and its application to privatization in a transition economy by a new method: the MOORA method, Control and Cybernetics, 35, pp. 445-469, 2006.

[24] Maniya, K. and Bhatt, M., A selection of material using a novel type decision-making method: Preference selection index method. Materials and Design, 31 (4), pp. 1785-1789, 2010. DOI: 10.1016/j.matdes.2009.11.020

[25] Ho, W., Xu, X. and Dey, P., Multi-criteria decision making approaches for supplier evaluation and selection: A literature review. European Journal of Operational Research, 202 (1), pp. 16-24, 2010. DOI: 10.1016/j.ejor.2009.05.009

[26] Govindan, K., Rajendran, S., Sarkis, J. and Murugesan, P., Multi criteria decision making approaches for green supplier evaluation and selection: A literature review, Journal of Cleaner Production, article in press, DOI: 10.1016/j.jclepro.2013.06.046, 2013. DOI: 10.1016/j.jclepro.2013.06.046

[27] Liou, J., Chuang, Y.-C. and Tzeng, G.-H., A fuzzy integral-based model for supplier evaluation and improvement, Information Sciences, 266, pp. 199-217, 2014. DOI: 10.1016/j.ins.2013.09.025

[28] Aksoy, A., Sucky, E. and Öztürk, N., Dynamic strategic supplier selection system with fuzzy logic, Procedia - Social and Behavioral Sciences, 109, pp. 1059-1063, 2014. DOI: 10.1016/j.sbspro.2013.12.588

[29] Ayhan, M., A fuzzy AHP approach for supplier selection problem: A case study in a Gear motor company, International Journal of Managing Value and Supply Chains, 4 (3), pp. 11-23, 2013. DOI: 10.5121/ijmvsc.2013.4302

[30] Chai, J., Liu, J. and Ngai, E., Application of decision-making techniques in supplier selection: A systematic review of literature, Expert Systems with Applications, 40 (10), pp. 3872-3885, 2013. DOI: 10.1016/j.eswa.2012.12.040

[31] Patil, S. and Kant, R., A fuzzy AHP-TOPSIS framework for ranking the solutions of knowledge management adoption in supply chain to overcome its barriers, Expert Systems with Applications, 41 (2), pp. 679-693, 2014. DOI: 10.1016/j.eswa.2013.07.093

[32] Beg, I. and Rashid, T., Multi-criteria trapezoidal valued intuitionistic fuzzy decision making with choquet integral based TOPSIS, Opsearch, 51 (1), pp. 98-129, 2013. DOI: 10.1007/s12597-013-0134-5

[33] Behzadian, M., Khanmohammadi, S., Yazdani, M. and Ignatius, J., A state-of the-art survey of TOPSIS applications, Expert Systems with Applications, 39 (17), pp. 13051-13069, 2012. DOI: 10.1016/j.eswa.2012.05.056

[34] Önüt, S., Kara, S. and Isik, E., Long term supplier selection using a combined fuzzy MCDM approach: A case study for a telecommunication company, Expert Systems with Applications, 36 (2), pp. 3887-3895, 2009. DOI: 10.1016/j.eswa.2008.02.045

[35] Rex, E., Wu, T. and Shunk, D., A stochastic AHP decision making methodology for imprecise preferences, Information Sciences, 270, pp. 192-203, 2014. DOI: 10.1016/j.ins.2014.02.077

[36] Du, Y., Gao, C., Hu, Y., Mahadevan, S. and Deng, Y., A new method of identifying influential nodes in complex networks based on TOPSIS. Physica A, 399, pp. 57-69, 2014. DOI: 10.1016/j.physa.2013.12.031

[37] Kurka, T., Application of the analytic hierarchy process to evaluate the regional sustainability of bioenergy developments, Energy, 62, pp. 393-402, 2013. DOI: 10.1016/j.energy.2013.09.053

[38] Wang, T.-C. and Chen, Y.-H., Applying fuzzy linguistic preference relations to the improvement of consistency of fuzzy AHP, Information Sciences, 178,(19), pp. 3755-3765, 2008. DOI: 10.1016/j.ins.2008.05.028

[39] Vega, A., Aguarón, J., García-Alcaraz, J. and Moreno-Jiménez, J. Notes on Dependent Attributes in TOPSIS. Procedia - Computer Science, 31, pp. 308-317, 2014. DOI: 10.1016/j.procs.2014.05.273

[40] Ashtiani, B., Haghighirad, F., Makui, A. and Montazer, G., Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets, Applied Soft Computing, 9 (2), pp. 457-461, 2009. DOI: 10.1016/j.asoc.2008.05.005

[41] Villanueva-Ponce, R. and García-Alcaraz, J.L., Evaluation of technology using TOPSIS in presence of multi-collinearity in attributes: Why use the Mahalanobis distance, Revista de la Facultad de Ingeniería. Univ. Antioquia, 67, pp. 31-42, 2013.

[42] Li, K. and Wang, Z., Notes on multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment, Journal of Systems Science and Systems Engineering, 19 (4), pp. 504-508, 2010. DOI: 10.1007/s11518-010-5152-8

[43] Li, D.-F., Multiattribute decision-making models and methods using intuitionistic fuzzy sets, Journal of Computer and System Sciences, 70 (1), pp. 73-85, 2005. DOI: 10.1016/j.jcss.2004.06.002

[44] Liu, H.-W. and Wang, G.-J., Multi-criteria decision-making methods based on intuitionistic fuzzy sets, European Journal of Operational Research, 179 (1), pp. 220-233, 2007. DOI: 10.1016/j.ejor.2006.04.009

[45] Xu, Z. and Yager, R., Dynamic intuitionistic fuzzy multi-attribute decision making, International Journal of Approximate Reasoning, 48 (1), pp. 246-262, 2008. DOI: 10.1016/j.ijar.2007.08.008

[46] Chen, R.-Y., A problem-solving approach to product design using decision tree induction based on intuitionistic fuzzy, European Journal of Operational Research, 196 (1), pp. 266-272, 2009. DOI: 10.1016/j.ejor.2008.03.009

[47] Liao, H. and Xu, Z., Intuitionistic fuzzy hybrid weighted aggregation operators, International Journal of Intelligent Systems, 29 (11), pp. 971-993, 2014. DOI: 10.1002/int.21672

[48] Chen, Y. and Li, B., Dynamic multi-attribute decision-making model based on triangular intuitionistic fuzzy numbers, Scientia Iranica, 18 (2), pp. 268-274, 2011. DOI: 10.1016/j.scient.2011.03.022

[49] Yu, D., Group decision making based on generalized intuitionistic fuzzy prioritized geometric operator, International Journal of Intelligent Systems, 27, pp. 635-661, 2012. DOI: 10.1002/int.21538

[50] Yu, D., Wu, Y. and Lu, T., Interval-valued intuitionistic fuzzy prioritized operators and their application in group decision making, Knowledge-Based Systems, 30, pp. 57-66, 2012. DOI: 10.1016/j.knosys.2011.11.004

[51] Zhang, H. and Yu, L., MADM method based on cross-entropy and extended TOPSIS with interval-valued intuitionistic fuzzy sets, Knowledge-Based Systems, 30 (l), pp. 115-120, 2012. DOI: 10.1016/j.knosys.2012.01.003

[52] Boran, F., Genç, S., Kurt, M. and Akay, D., A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method, Expert Systems with Applications, 36, pp. 11363-11368, 2009. DOI: 10.1016/j.eswa.2009.03.039

[53] Xu, X., Intuitionistic fuzzy aggregation operators, IEEE Transactions on Fuzzy Systems, 15 (6), pp. 1179-1187, 2007. DOI: 10.1109/TFUZZ.2006.890678

[54] Zhang, X. and Xu, Z., A new method for ranking intuitionistic fuzzy values and its application in multi-attribute decision making, Fuzzy Optimization and Decision Making, 11 (2), pp. 135-146, 2012. DOI: 10.1007/s10700-012-9118-9

[55] Aloini, D., Dulmin, R. and Mininno, V., A peer IF-TOPSIS based decision support system for packaging machine selection, Expert Systems with Applications, 41 (5), pp. 2157-2165, 2014. DOI: 10.1016/j.eswa.2013.09.014

[56] Chen, T., The extended linear assignment method for multiple criteria decision analysis based on interval-valued intuitionistic fuzzy sets, Applied Mathematical Modelling, 38 (7-8), pp. 2101-2117, 2014. DOI: 10.1016/j.apm.2013.10.017

[57] Yue, Z., TOPSIS-based group decision-making methodology in intuitionistic fuzzy setting, Information Sciences, 277, pp. 141-153, 2014. DOI: 10.1016/j.ins.2014.02.013

[58] Atanassov, K., Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20, pp. 87-96, 1986. DOI: 10.1016/S0165-0114(86)80034-3

[59] Atanassov, K., New operations defined over the IFS, Fuzzy Sets and Systems, 61, pp. 137-142, 1994. DOI: 10.1016/0165-0114(94)90229-1

[60] Brauers, W., Zavadskas, J., Peldschus, F. and Turskis Z., Multi -objective decision-making for road design, Transport, 23 (3), pp. 183- 193, 2008. DOI: 10.3846/1648-4142.2008.23.183-193

[61] Kalibatas, D. and Turkis, Z., Multicriteria evaluation of inner climate by using MOORA method, Information Technology and Control, 37 (1), pp. 79-83, 2008.

[62] García, J., Villanueva, R., Alvarado, A. and Maldonado, A., Evaluación y Selección de Proveedores Usando el Método MOORA. Academia Journals, (2), pp. 454-459, 2012.

[63] Stanujkic, D., Magdalinovic, N., Stojanovic, S. and Jovanovic, R., Extension of ratio system part of MOORA method for solving decision-making problems with interval data, Informatica, 23 (1), pp. 141-154, 2012.

 

L. Pérez-Domínguez was born in Jalapa, Tabasco, México, on August 1, 1977. Completed a BSc. in industrial engineering at Instituto Tecnológico de Villahermosa, Tabasco, México in 2000 and MSc. degrees in industrial engineering from Instituto Tecnológico de Ciudad Juárez, Chihuhua, México, in 2003 respectively. He is currently a Doctoral student in the Science of Engineering, at the Autonomous University of Ciudad Juárez, Chihuahua, México. His research interests include multiple criteria decision making and continuous improvement tools applied in the manufacturing field.

A. Alvarado-Iniesta is currently an assistant professor in the Department of Industrial and Manufacturing Engineering in the Autonomous University of Ciudad Juarez, Mexico. He obtained his Bachelor's degree in Electronics Engineering, a MSc. degree in Industrial Engineering and a PhD. in Engineering with specialization in Industrial Engineering. His research interests are in the optimization and control of manufacturing process such as plastic injection molding. His areas of research focus on methodologies such as fuzzy logic and artificial neural networks employed as surrogate models, and evolutive algorithms as well as swarm intelligence.

I. Rodríguez-Borbón is currently an assistant professor in the Department of Industrial and Manufacturing Engineering in the Autonomous University of Ciudad Juarez, Mexico. He obtained his PhD. in Industrial Engineering. His researches are related to quality and reliability fields.

O. Vergara-Villegas was born in Cuernavaca, Morelos, México, on July 3, 1977. He completed his BSc. degree in computer engineering at the Instituto Tecnológico de Zacatepec, México, in 2000; his MSc. in computer science at the Center of Research and Technological Development (CENIDET) in 2003 and PhD. in computer science at CENIDET in 2006. He currently serves as a professor at the Autonomous University of Ciudad Juárez, Chihuahua, México. He has been a senior member of the IEEE Computer Society since 2012. His fields of interest includes pattern recognition, digital image processing, augmented reality and mechatronics.