Un enfoque de polinomio de expansión de caos al análisis de la incerteza en elementos estructurales visco elásticos

A polynomial chaos expansion approach to the analysis of uncertainty in viscoelastic structural elements

La propagación de la incerteza en sistemas mecánicos a través de modelos de cálculo fue analizado en este artículo por series de polinomios estocásticos de variables aleatorias estandarizadas llamados Polinomios de expansión de caos. Este artículo tuvo como objetivo simular la propagación de la incerteza en modelos mecánicos más complejos tales como estructuras visco elásticas el cual implica caracterización de parámetros dependientes del tiempo de materiales, interconversión de funciones matemáticas a través de transformada de Laplace, y resolución de la ecuación constitutiva mediante integrales de convolución. La aplicación de series de polinomios Hermite multidimensionales permitió la predicción de la aleatoriedad del vector de salida. En este trabajo se demostró que un polinomio de expansión de caos estima adecuadamente la propagación de la incerteza de las variables aleatorias. Los resultados mostraron que el parámetro material no solo afecta los coeficientes de variación del desplazamiento, sino también dicta el tipo y propagación de las colas de la función de densidad de probabilidad para la respuesta estructural.

The uncertainty propagation in mechanical systems through model calculations was analyzed in this article by stochastic polynomial series of standardized random variables called Polynomial Chaos Expansion. This paper aimed to simulate the propagation of uncertainty in more complex mechanical models such viscoelastic structures which involves time dependent parameters characterization of materials, interconversion of mathematical functions through Laplace transform, and resolution of the constitutive equation through convolution integrals. The application of multi-dimensional Hermite polynomials series allowed the prediction of the randomness of the output vector. In this work it was demonstrated that a polynomial chaos expansion accurately estimated the spread of uncertainty of the random variables. The results showed that the material parameters not only affects the coefficient of variation of the displacements, but also dictates the type and spread of the tails of the probability density function for the structural output.

DOI: https://doi.org/10.15446/dyna.v83n199.53834

Francisco Evangelista Jr ^a & Nelson Afanador-García ^b

^a Faculdade de Tecnologia, Universidade de Brasília, Brasília, Brasil. fejr.unb@gmail.com
^b Faculdade de Tecnologia, Universidade de Brasília, Brasília, Brasil. Facultad de Ingeniería, Universidad Francisco de Paula Santander, Ocaña, Colombia. nafanadorg@aluno.unb.br, nafanadorg@ufpso.edu.co

Received: October 28^th, 2015. Received in revised form: March 20^th, 2016. Accepted: August 1^rd, 2016.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
The uncertainty propagation in mechanical systems through model calculations was analyzed in this article by stochastic polynomial series of standardized random variables called Polynomial Chaos Expansion. This paper aimed to simulate the propagation of uncertainty in more complex mechanical models such viscoelastic structures which involves time dependent parameters characterization of materials, interconversion of mathematical functions through Laplace transform, and resolution of the constitutive equation through convolution integrals. The application of multi-dimensional Hermite polynomials series allowed the prediction of the randomness of the output vector. In this work it was demonstrated that a polynomial chaos expansion accurately estimated the spread of uncertainty of the random variables. The results showed that the material parameters not only affects the coefficient of variation of the displacements, but also dictates the type and spread of the tails of the probability density function for the structural output.

Keywords: Stochastic analysis; Polynomial chaos expansions; Viscoelasticity; relaxation modulus.

Resumen
La propagación de la incerteza en sistemas mecánicos a través de modelos de cálculo fue analizado en este artículo por series de polinomios estocásticos de variables aleatorias estandarizadas llamados Polinomios de expansión de caos. Este artículo tuvo como objetivo simular la propagación de la incerteza en modelos mecánicos más complejos tales como estructuras visco elásticas el cual implica caracterización de parámetros dependientes del tiempo de materiales, interconversión de funciones matemáticas a través de transformada de Laplace, y resolución de la ecuación constitutiva mediante integrales de convolución. La aplicación de series de polinomios Hermite multidimensionales permitió la predicción de la aleatoriedad del vector de salida. En este trabajo se demostró que un polinomio de expansión de caos estima adecuadamente la propagación de la incerteza de las variables aleatorias. Los resultados mostraron que el parámetro material no solo afecta los coeficientes de variación del desplazamiento, sino también dicta el tipo y propagación de las colas de la función de densidad de probabilidad para la respuesta estructural.

Palabras claves: Análisis estocástico; Polinomios de expansión de caos; Viscoelasticidad; módulo de relajación.

---

1. Introducción

La determinación de la incertidumbre es fundamental en la modelación de sistemas mecánicos especialmente por su aplicación regular. La incertidumbre puede ser atribuida a, i) aleatoriedad inherente o a la impredecibilidad del sistema físico, ii) simplificaciones y aproximaciones en la formulación del modelo, iii) un conocimiento parcial de las variables de entrada, debido a la inexactitud o insuficiencia de datos (incertidumbre en los datos). Existen otras clasificaciones de incertidumbre que están fuera del alcance de este trabajo, y que están disponibles en la literatura para el lector interesado [20].

La incertidumbre en los resultados del modelo, esta normalmente centrado en la incertidumbre de los datos y consiste de, i) caracterización de las variables del modelo vía sus funciones de densidad de probabilidad (fdp), y ii) la propagación de estas fdp a través de la ecuación del modelo para obtener las fdp de la variable de salida seleccionada.

Dos enfoques comúnmente utilizados para establecer la propagación de la incertidumbre en los parámetros del modelo son, el método analítico y el método de Monte Carlo. En el método analítico [1,13] la incertidumbre en la salida es representada explícitamente como funciones de incertidumbre en las variables de entrada; son principalmente utilizados en pequeños rangos de incertidumbre en las variables y no pueden ser usados en complejos modelos no lineales. El método de Monte Carlo [10, 16] involucra un número suficientemente grande de corridas del modelo con un muestreo aleatorio de las variables de entrada, estimadas mediante las fdp con gran costo computacional y tiempo especialmente para el caso que envuelve un número grande de incertidumbre en los datos. Por lo tanto, hay la necesidad de utilizar otros métodos computacionales más eficientes para la estimación de la incerteza en modelos complejos, que utilicen un número significativamente reducido de soluciones. Estos métodos utilizan técnicas de reducción de varianza tales como importance sampling [29] y simulación de Monte Carlo Markov Chain [11] y han sido propuestos para reducir el número de corridas sin comprometer la precisión.

Otra estrategia que puede ser utilizada como una versión sustituta, aproximada y más barata, son los polinomios Hermite multidimensionales (comúnmente llamados Polinomios de expansión de Caos, PEC) [4,35,27]. El PEC pueden ser clasificados dentro de dos enfoques: formulación intrusiva y no intrusiva; en la formulación intrusiva la incerteza es expresada explícitamente dentro del análisis del sistema que se está investigando (utiliza el Método de Galerkin [30]), en la formulación no intrusiva el PEC son usados para crear superficies de respuesta (llamado método de superficie de respuesta estocástico [18]) sin interferir en el análisis del sistema [7].

La literatura no reporta un estudio sobre el impacto de la incertidumbre asociada con el ajuste de parámetros del material de la función de fluencia y/o módulo de relajación en la respuesta final dependiendo del tiempo. El único artículo encontrado en este tema es el trabajo de [27,23] quien llevó a cabo un estudio paramétrico y destacó la importancia de considerar aspectos meteorológicos en la respuesta viscoelástico. Sin embargo, su trabajo fue basado en simulación de Monte Carlo el cual demando miles de simulaciones para determinar la variabilidad de la salida, más el número de simulaciones no fue lo suficiente para proporcionar con precisión las funciones de densidad de probabilidad para la respuesta de un proceso estocástico.

El presente trabajo analizó la aleatoriedad de las variables de tres parámetros del modelo sólido (E_¥, E₁ y r₁) en la determinación del módulo de relajación utilizando PEC como una formulación no intrusiva y determinando los coeficientes del polinomio mediante la implementación del método de la colocación probabilística [32,33]. La principal contribución de este trabajo fue la cuantificación de la propagación de la incerteza de los tres parámetros del modelo sólido sobre la caracterización integral del módulo de relajación y también en la respuesta estructural tal como el desplazamiento en problemas de contorno visco elástico. Esta caracterización probabilística fue alcanzado mediante la determinación de las funciones de densidad acumulativa (fdc) y/o funciones de densidad de probabilidad (fdp) con las colas bien definidas. Esto permitió una cuantificación completa de la incertidumbre en modelos de materiales más complejos como el visco elástico que envuelve la convolución del módulo de relajación para el cálculo de deflexiones.

2. Materiales y métodos

La propagación en la incertidumbre de los parámetros de entrada del modelo es llevada a cabo mediante: i) las incertidumbres en los parámetros de entrada son expresados en términos de un conjunto de variables aleatorias, ii) la forma del funcional es asumida para la salida seleccionada, iii) los parámetros de la aproximación del funcional son determinísticos. La incertidumbre en las variables aleatorias puede ser analizada desde diferentes métodos de simulación, uno de ellos es el Método de Monte Carlo.

2.1. Método de Monte Carlo

El Método de Monte Carlo (MMC) envuelve un número significativamente grande de simulaciones del modelo analítico o numérico con combinaciones de las variables aleatorias; dada la distribución de probabilidad y los parámetros de la distribución, las variables aleatorias pueden ser obtenidas mediante la implementación del método de transformación inversa [22], véase ec. (1). Para establecer los valores de las variables aleatorias se siguió el siguiente algoritmo: [19]

Dada la expresión donde g representa el modelo en consideración, X es un vector que representa la incerteza en las variables de entrada y Y representa un vector de salida estimado, así,

1. Define las distribuciones de probabilidad y los parámetros de la distribución de cada variable aletoria de entrada.
2. Genera un valor de muestreo de cada una de las j variables aplicando el método de la transformación inversa.
3. Evalúa la respuesta desde el modelo analítico o numérico usando los valores de .
4. Repita los pasos ii) y iii) para generar una distribución de probabilidad de la respuesta. El número de simulaciones (N) es elegido tal que la distribución de salida converja a un valor establecido.

En el presente trabajo, la simulación del modelo estocástico (E(t) y d) utiliza el método de Monte Carlo como una base de referencia para validar la precisión del enfoque basado en PEC [13,19,22,30].

2.2. Método de superficie de respuesta estocástico

El método de superficie de repuesta estocástico (MSRE) puede ser interpretado como una adición del Método de superficie de respuesta (determinístico, MSR), donde su principal diferencia son las entradas pues ellas son variables aleatorias. [17]

La Fig. 1 ilustra un diagrama de flujo donde se indican las etapas a seguir en el MSRE [15, 18]. Los 4 grandes pasos del MSRE son:

1. Representación de la entrada estocástica.
2. Representación del funcional de salida.
3. Estimación de los coeficientes desconocidos del polinomio de expansión de caos.
4. Estimación de la estadística de salida y análisis de confiabilidad.

2.3. Representación de la entrada estocástica

Las entradas estocásticas deben ser representadas en términos de variables aleatorias estándar (VAE). Las variables aleatorias con distribución de probabilidad normal o gamma son frecuentemente elegidas para representar la incerteza en la entrada debido a la tratabilidad matemática de las funciones de estas variables aleatorias [9,24]. En el presente trabajo, estas variables aleatorias son referidas a variables aleatorias normal estándar distribuidas idéntica e independientes , donde n es el número de entradas independientes y tiene media cero y varianza uno. con n resultados del vector aleatorio normal estándar y donde para cada resultado de la transformación isoprobabilistica produce un vector de variables aleatoria de entrada .

Donde es la fdc normal estándar y son las fdc marginales de

Para variables no correlacionadas la incertidumbre en la i-ésimo entrada del modelo X_i, es expresada como una función de la i-ésima variable aleatoria normal estándar que puede ser determinada mediante transformación directa de la entrada en términos de las VAE o en series aproximadas. Devroye [9] presenta técnicas de transformación y aproximación para un amplio número de variables aleatorias; variables aleatorias no encontradas en la literatura pueden ser aproximadas usando técnicas de expansión de series [33]. La transformación de 12 tipos de distribución frecuentemente usadas, son resumidas en la Tabla 1.

2.4. Representación del funcional de salida

La salida en un modelo mecánico está influenciada por todas las entradas. Una representación del funcional general de la incertidumbre en la salida del modelo debe ser tenida en cuenta en la incertidumbre de todas las entradas. Una aproximación del funcional ampliamente usado, son los polinomios de expansión de caos sobre el conjunto , dado por:

Donde y es la salida aleatoria del modelo, son constantes determinísticas a ser halladas, n es el número de variables aleatorias usadas para representar la incertidumbre de la entrada del modelo, son variables aleatorias normales estándar independientes y son polinomios Hermite multidimensionales de grado p. Los polinomio de caos pueden ser construidos apartir de la función generadora de los polinomios de Hermite de grado para el orden p está dado por:

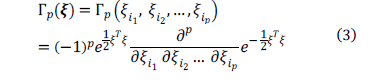
donde es el vector que representa la incertidumbre en la entrada. Los polinomios Hermite definidos sobre es ortogonal con respecto al producto interno definido como la esperanza del producto de dos variables aleatorias [13], es decir que, el vector de orden n es ortogonal con el vector de orden n-1 y n+1.

Es conocido que el polinomio Hermite multidimensional forma una base ortogonal y los PEC convergen en Si es un vector aleatorio normal estándar, el polinomio Hermite multivariante esta normalizado [4].

En la práctica, los PEC son truncados a un número finito de términos (N) para un PEC de orden p y n número de variables aleatorias de entrada, el número de coeficientes desconocidos es:

2.4.1. Estimación de los coeficientes desconocidos del polinomio de expansión de caos.

El enfoque original en la determinación de los coeficientes de polinomios de expansión de caos truncados fue el enfoque Galerkin [13] utilizado en sistemas intrusivos para la solución de problemas mecánicos. Los métodos de solución para sistemas no intrusivos pueden ser clasificados en:

• Método de la proyección, hace uso directo de las propiedades de la base de PEC [13].
• Método de la colocación estocástica, está basado en la interpolación de Lagrange en el espacio estocástico. [33,36,37].
• Método de la regresión, soluciona para polinomios de alto grado la inestabilidad que se presenta en el método de la colocación [17], y recientemente mejorado a través de la estimación del error y la adaptabilidad [3,5,6].

El método de la colocación estocástica (MCE o probabilística) tiene la ventaja que desacopla la evaluación de la respuesta determinística y el análisis estocástico; análisis realizado en los puntos de colocación de más alta probabilidad y seleccionados tal que haya simetría respecto al origen. Por razones de inestabilidad del método para polinomios de alto orden fue utilizado el método de la regresión o método de la colocación basado en la regresión propuesto por Isukapalli [18] frecuentemente usado para estimar los coeficientes desconocidos del polinomio de expansión de caos, para mayores detalles el lector puede consultar las referencias [18,31].

En el método de la colocación basado en regresión el número de puntos seleccionados deberá ser dos veces el número de coeficientes desconocidos a ser estimados en el polinomio Hermite a fin de obtener un estimador robusto del coeficiente desconocido [18] enfoque usado en los Polinomios de expansión de caos en elementos viscoelásticos analizado en la sección 3.

Cuando N es un conjunto de puntos de colocación seleccionados, la salida en cada conjunto de puntos de colocación puede ser obtenida. Reescribiendo en forma matricial,

Donde Z es una matriz en espacio independiente de dimensión , donde el polinomio Hermite es evaluado en el conjunto de puntos de colocación seleccionados. C es el vector de coeficientes desconocidos de dimensión . Entonces la ec. (6) puede ser reescrita y solucionada,

Los PEC es un método espectral [4,13,15,18,24,27] que permite la propagación de la incertidumbre de las variables aleatorias de entrada mediante la construcción de funcionales no lineales dependiente de la solución [13,21] a la variable aleatoria de salida, permitiendo cuantificar la incertidumbre de la salida mediante la pdf [32]. La convergencia de la solución aproximada es medida mediante la comparación de los PEC de diferente grado [17] o entre PEC y SMC [21,31], es por todo lo anterior que esta garantizada la precisión de los resultados. La convergencia espectral va a depender de la alta diferenciabilidad de las funciones de Hermite contenidas en cada variable aleatoria normal estándar [36] donde la solución aproximada converge en el error cuadrático medio.

2.4.2. Estimación de la estadística de salida y análisis de confiabilidad.

Determinado los coeficientes del polinomio, es posible evaluar las propiedades estadísticas de la salida, tales como fdp, función de distribución cumulativa (fdc), varios momentos y correlación entre la entrada y la salida. La probabilidad de falla y su correspondiente índice de confiabilidad puede ser hallada para la función de estado límite definida en el modelo de salida y representada como un polinomio de expansión de caos.

2.5. Viscoelasticidad

Los materias visco elásticos lineales se caracterizan por tener un comportamiento intermedio entre un sólido elástico lineal y un fluido viscoso (simple o Newtoniano) Un material sólido elástico lineal cumple la ley de Hooke y por tanto, es cierto que los esfuerzos son proporcionales a la deformación (independiente del tiempo) es decir,

Donde E es la constante de proporcionalidad y puede ser representado por un resorte. Fluidos viscosos simples se caracterizan por tener viscoelasticidad constante a lo largo del tiempo y generalmente son representados por un amortiguador. Un fluido viscoso sigue la ley de Newton por lo tanto al someter un fluido a un esfuerzo de corte el cuerpo presenta una tasa de deformación proporcional a la tensión aplicada. La relación constitutiva de los fluidos Newtonianos es,

Donde representa la viscoelasticidad. Los materiales viscoelásticos tiene la capacidad de almacenar energía deformación como un sólido elástico y disipar esta energía siguiendo la ley de los fluidos viscosos.

Realizada una analogía mecánica entre los materiales eléctricos y visco elásticos, donde el módulo de elasticidad es equivalente a la capacitancia del circuito (mide la capacidad de almacenamiento de energía) y la resistencia del circuito es comparable con la viscoelasticidad (mide la capacidad para disipar energía) es usada para visualizar los diferentes modelos visco elásticos que se encuentran en la literatura [12]. El modelo de Boltzmann utilizado en este trabajo e ilustrado en la Fig. 2 considera un elemento de Kelvin y un elemento elástico simple trabajando en serie [8,25] y tiene la siguiente ecuación diferencial característica del sistema:

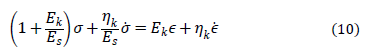
Aplicando un tensión constante a lo largo del tiempo y considerando las condiciones de contorno para el tiempo , y resolviendo la ec. (10) se obtiene;

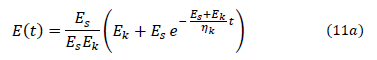
donde E(t) es el módulo de relajación y haciendo

Reemplazando en la ec. (11a) se obtiene;

Es posible expresar la función de fluencia en términos del módulo de relajación 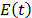mediante los métodos de interconversión [25, 26], es decir

donde D(t) es la función de fluencia y haciendo

Reemplazando en la ec. (13a) se obtiene;

3. Resultados

3.1. Polinomios de expansión de caos en elementos viscoelásticos: Módulo de relajación

El modelo del módulo de relajación considera variables aleatorias de entrada que siguen una distribución de probabilidad normal para distribuidas idéntica e independientemente, debido a la incerteza epistémica de las distribuciones de probabilidad de los datos que surgen de los pocos ensayos de laboratorio. La pdf normal fue asumida para estos valores teniendo en cuenta la entropía estadística que dice, "cuando son conocidos dos parámetros como el promedio, la desviación estándar y se desconoce la distribución, la máxima entropía estadística es alcanzada con la distribución de probabilidad normal" [2,14]. En la Tabla 2 se establecen los parámetros de cada variable.

Las variables aleatorias normales estadísticamente independientes serán expresadas en términos de variables aleatorias normal estándar, es decir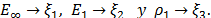

La aplicación del MSRE para la estimación de la incertidumbre en la determinación del módulo de relajación 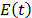puede ser expresado en términos de polinomios de expansión de caos.

El efecto de la incerteza en las variables de entrada sobre el módulo de relajación E(t) es analizado usando el MSRE , y los coeficientes del PEC son determinados mediante el método de la colocación basado en la regresión, el cual requirió 20 soluciones de la ec. (12) para estimar los coeficientes determinísticos, es decir, atendiendo el requerimiento del método de la colocación basado en la regresión propuesto por Isukapalli [18]. Una comparación de las fdp de E(t) hallado mediante el método de Monte Carlo utilizando la ec. (12) y realizando 1.000.000 simulaciones por variable aleatoira, mientras que utilizando PEC (ec.(2)) fueron necesarias sólo 50.000 simulaciones por variable aleatoria normal estandar para tener una buena estimativa de la fdp de E(t) dado que el error fue de 3.5665E-20 y el coeficiente de determinación R² = 1, halladas mediante la realización de un programa en el ambiente de programación, es indicado en la Fig. 3 para un V = 0.1. La simulación del modelo estocástico del Módulo de Relajación vía Monte Carlo y la simulación realizada vía Polinomios de expansión de caos llegaron al mismo resultado, sólo que PEC requirió el 5 % de los datos utilizados por Monte Carlo. Demostrada la eficiencia del método de la colocación probabilística en la determinación de los coeficientes del PEC lo cual corresponde a lo reportado por la literatura especializada como un método robusto que permite determinar los coeficientes mediante una transformación de espacios probabilísticos de la variable original a variable normal estándar [16,17,28,31].

Esta investigación utilizó PEC de grado 2 para la determinación de la incertidumbre del módulo de relajación E(t). Las distribuciones de salida fueron estimadas utilizando el estimador de máxima verosimilitud para establecer la mejor función de densidad de probabilidad que se ajusta a los datos obtenidos de la simulación del modelo. Los resultados indicaron que el PEC de dimensión tres y segundo grado es computacionalmente más eficiente que el Método de Monte Carlo crudo.

Las fdp de la salida del modelo pata t=1 s es determinada utilizando los PEC de dimensión 3 y segundo grado y están dados en la Fig. 4 para todos los coeficientes de variación dados en la Tabla 2, los resultados obtenidos indican que el promedio de E(t=1 s) es de 1.01 dinas/cm² y su distribución de probabilidad es normal para todos los V(s), mientras que las desviaciones estándar varían de acuerdo al V, es decir que para V=0,40 de las variables aleatorias de entrada, la dispersión en la salida encontrada fue de V=0,3976.

La fdp del modelo estocástico estacionario para t=3E+4 s mostrada en la Fig. 6 para todos los coeficientes de variación dados en la Tabla 2, indican que el promedio de E(t=3.0E+04 s) varia desde 0.054 hasta 0.021 dynas/cm² mientras que las distribuciones de probabilidad son lognormal para V=0.1 a 0.4.

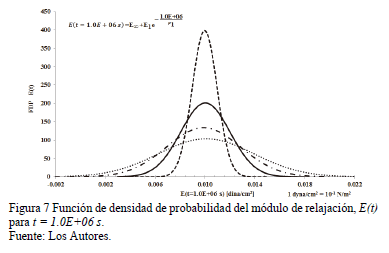
Por último la fdp del módulo de relajación para E(t=1.0E+06 s) sigue una distribución de probabilidad normal, encontrandose que el valor promedio para todos los V analisados es de 0.01 dynas/cm² y la desviación estándar desde 0.001 a 0.0038 para V igual 0.1 a0.4 respectivamente. Las fdp del modelo de salida son dadas en la Fig. 7. El módulo de relajación E(t) presenta una variación en el tiempo importante, no es constante y por el contrario puede tener alta variación especialmente cuando t está cerca de los 3.0E+04 s generando con esto grandes variaciones entre los coeficientes de variación de las variables de entrada y la variable de salida E(t).

Existe una relación lineal entre los coeficientes de variación de las variables de entrada y el coeficiente de variación del módulo de relajación, para un tiempo t igual a 1 s, 3.0E+03 s y 1.0E+06 s; la variación en la variable aleatoria de salida es aproximadamente la misma a la observada en las variables aleatorias de entrada (V = 0.1, 0.2, 0.3 y 0.4), véase Fig. 8. Excepto para t=3.0E+03 s y fijando en el promedio , la relación entre los coeficientes de variación de las variables aleatorias de entrada y salida disminuye, tanto que para una V = 0.4 de las variables aleatorias de entrada se obtiene una variación igual a 0.33 para la variable estocástica de salida E(t). Existe mayor variabilidad en el módulo de relajación E(t) para el tiempo t igual a 3.0E+04 s y está es 2.5 veces los coeficientes de variación de las variables aleatorias de entrada, dada la alta complejidad del modelo toda vez que el tiempo es exponente y define una zona de variación no lineal de E(t).

3.2. Polinomios de expansión de caos en elementos viscoelásticos: Deflexión en el tiempo en viga biapoyada

El modelo de deflexión considera variables determinísticas para geometría, carga y sus valores se indican en la Tabla 3.

El módulo de relajación E(t) incide en el cálculo de la deflexión, y puede pasar fácilmente del 1.06% de la deflexión estimada elástica en el centro de la luz de una viga biapoyada para un tiempo t=1 s y considerando la variable 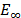de forma determinística (valor promedio Tabla 2), al 100 % de la deflexión estimada para el caso elástico con t=1.0E+06 s, e idénticas consideraciones para las variables de entrada 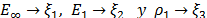, los resultados se indican en la Fig. 9 y representa el desplazamiento normalizado respecto al centro del vano.

Ahora bien, teniendo en cuenta la incertidumbre en las variables de entrada y considerando las demás variables determinísticas (ver Tablas 2 y 3) para el cálculo de la deflexión en el centro de una viga biapoyada y teniendo la función de fluencia expresado en la ec. (12) la deflexión en la viga biapoyada es determinada mediante la ec. (15).

Para llevar a cabo el presente trabajo de investigación se desarrolló un algoritmo en ambiente de programación MatLab versión R2013a que determina el polinomio Hermite y sus coeficientes para una variación V, así pues para V=0.1 la ec. (15) puede ser expresada en términos de variables aleatorias normales estándar, es decir en función de polinomios Hermite.

La deflexión normalizada en el centro de la luz de una viga biapoyada para cualquier coeficiente de variación sigue una distribución de probabilidad lognormal producto de la simulación del PEC. Para t=1 s el promedio en la deflexión normalizada es de 0.0105 y desviación estándar de 0.0010 con V=0.1 y puede aumentar hasta 0.0134 de promedio y 0.0055 de desviación estándar para V=0.4, véase Fig. 10, es decir, alcanza un incremento en el promedio de la deflexión normalizada del 21.55%, mientras que el percentil 50 no presenta cambio significativo producto de la simulación de PEC. La deflexión esperada que más se repite es del 1.06% de la deflexión máxima elástica en el centro de la luz (véase Fig.9, 10), pero puede alcanzar hasta el 1.4% de la deflexión máxima elástica.

El aumento en el tiempo t a 3.0E03 s genera una disminución en el módulo de relajación produciendo un aumento en la deflexión estimada; por ejemplo el promedio de la deflexión normalizada aumenta de 0.2868 para V=0.1 a 0.3960 para V=0.4, es decir hay un incremento en la deflexión normalizada del 27.56%, véase Fig. 11. La moda de las deflexiones normalizadas varia 0.259 para V=0.1 a 0.200 para V=0.4, representando un decremento en la deflexión del 18.92%., es decir que a mayor variación en las variables de entrada el valor que más se repite disminuye hasta llegar a 18.92 % de la deflexión máxima elástica esperada, pero puede tener deflexiones aún mayores si V aumenta.

Para t=3.0E+04 s la función de fluencia aumenta, mudando rápidamente los promedios de la deflexión normalizada, véase Figs. 11, 12. El aumento en el promedio de las deflexiones estimadas desde t=3.0E+03 s a 3.0E+04 s con V=0.4 de las variables aleatoria de entrada es del 68.51%,un aumento algo similar se presenta al estudiar la varianza de la deflexión normalizada (variable estocástica de salida, ) para t=3.0E+04 s y V=0.1, es del 0.00124 mientras que para V=0.4 es de 0.0430 presentándose un incremento del 97.1 %.

La distribución de las deflexiones normalizadas para t=1.0E+06 s siguen un distribución de probabilidad lognormal para V=0.1 hasta 0.4, con promedios de la deflexión que varían desde 1.057 hasta 1.336 respectivamente, con un incremento del 20.86%. El parámetro estadístico que sufrió mayor variación fue la varianza de E(t), pues para V=0.1 fue de 0.0105 y para V=0.4 fue de 0.301 véase Fig. 13, es decir obtuvo un aumento en la dispersión de las deflexiones esperadas del 96.50%.

La variación V en las variables aleatorias de entrada (E_¥, E₁ y r₁) para los tiempo t=1, 3.0E+03, 3.0E+04, 1.0E+06 s y fijando t=3E+03 y r₁=1E+04 produce diferentes variaciones en la deflexión normalizada respecto a la deflexión en el centro de una viga sometida a carga uniformemente distribuida (determinística). Esta variación en la salida puede llegar a ser grande como se indica en la Fig. 14, por ejemplo para t=3.0E+03 s y V=0.4 la variación de d_N puede llegar ser del 0.6 con distribución de probabilidad lognormal. La variación de la deflexión normalizada tiene un comportamiento no lineal y puede ajustarse a una distribución parabólica (de segundo orden) para todos los tiempos t.

Esta investigación estableció que para variaciones V = 0.3 y 0.4 en t = 3.0E+04 s la deflexión normalizada es mayor a la deflexión elástica esperada y para t = 1.0E+06 s la deflexión puede ir desde 1.01 hasta 1.30 veces la deflexión elástica esperada para V = 0.1 a 0.4 respectivamente, véase Fig. 15. Si consideramos todas las variables que intervienen en el proceso estacionario estocastico, definido por la ec. (15) con márgenes de variación similares a los anteriormente expuestos, estos valores de deflexión normalizada incrementen aún más.

4. Discusión

Se presenta alta variación en los valores de deflexión máximos probables, pues ellos pueden variar desde 3.5% hasta 350% de la deflexión máxima elástica para t=1 s hasta 1E+6 s respectivamente; para los t=3.0E+04 s y 1.0E+06 s los valores de deflexión máximos probables no aumentan, más si su probabilidad, contrario a lo observado para t=1 s y t=3.0E+03 s.

No existe una relación directamente proporcional entre la variación en las variables de entrada y la variación en la variable de salida (), es decir para coeficientes de variación mayor a 20% se esperan una dispersión en la variable estocástica de salida aun mayor llegando a ser hasta del 60% para V=0.4 con t=3.0E+04 s y 1.0E+06 s véase Fig. 14, mientras que para otros tiempos la relación entre V de las variables aleatorias de entrada y las variable estocástica de salida es directamente proporcional y similar.

Es decir que para un tiempo t igual 3.0E+04 s se tiene la mayor variabilidad en el módulo de relajación y esta a su vez genera una alta variación en la deflexión para cualquier 0 ≤ x ≤ L. La variación en la deflexión puede representar un peligro para las construcciones civiles que no tengan un buen control de calidad en materiales, mano de obra y equipamiento, pues ello puede incrementar hasta en un 60% las deflexiones previstas por el diseñador, véase Fig. 14.

5. Conclusiones

Este artículo demostró la eficiencia y precisión de PEC acoplado con técnicas de superficie de respuesta para simular variables estocásticas con pocas rodadas para determinar la respuesta estructural de las propiedades de los materiales a través de la modelación numérica/matemática visco elástico. Esta característica fue crucial para problemas visco elásticos, ya que la propagación de la incertidumbre de los parámetros ajustados de los datos de laboratorio se propaga a través de la interconversión de la representación matemática visco elástico (E(t) a D(t)) y modelación numérica de las ecuaciones constitutivas las cuales consisten de convolución matemática sobre el tiempo. Aunque este trabajo se centró en solo el modelo sólido de tres parámetros para materiales visco elásticos mecánicos, se demostró que la variabilidad en los ajustes experimentales impacta en la interconversión del módulo de relajación (E(t)) después de la transformación de Laplace y causa la propagación relevante de la incerteza a través de la modelación.

Los resultados también mostraron que la variabilidad en el módulo de relajación, E(t) no es único en el tiempo, pero depende del tiempo t_i en el cual el módulo de relajación es evaluado E(t = t_i). El coeficiente de variación para E(t) incrementa para la parte de descenso intermedia de la curva E(t) más que para el tiempo t_i inicial y final.

El máximo incremento en la varianza de la deflexión normalizada esperada para una viga biapoyada con carga uniformemente distribuida se presenta en t=3.0E+03 s, cuando todas las tres variables aleatorias (E_¥, E₁ y r₁) son relevantes en la determinación de E(t), más que en los últimos tiempos (es decir t=1.0E+06 s) cuando solamente E_¥ es relevante para la relajación visco elástico. La variación en el módulo de relajación E(t) puede generar deflexiones importantes no previstas cuando se aplican cargas a temprana edad (pudiendo ser consideradas probabilísticas, utilizando integral de convolución), estas deflexiones pueden ser evaluadas si se consideran materiales visco elásticos y aún más si se consideran todas las variables aleatorias. Técnicas como Polinomios de expansión de caos disminuye el costo computacional con poca o ninguna pérdida de precisión y pueden ser aplicados en cualquier sistema mecánico.

Agradecimientos

Los autores agradecemos a la Facultad de Tecnología de la Universidad de Brasilia, Brasil; al Programa de Posgraduación en Estructuras y Construcción Civil por todo el apoyo recibido y la Coordinación de mejoramiento de personal de nivel superior-CAPES.

Referencias

[1] Adomian, G., Applied Stochastic Processes, New York, Academic Press, 1980.

[2] Bendat J.S. and Piersol A.G., Random data analysis and measurement procedures, Wiley, 2^nd Edition, New Jersey, USA, 2008.

[3] Blatman, G., Adaptive sparse polynomial chaos expansions for uncertainty propagation and sensitivity analysis. Ph.D. Thesis, Universite Blaise Pascal, Clermont-Ferrand, Aubière, France, 2009.

[4] Blatman, G. and Sudret B., Sparse polynomial chaos expansions and adaptive stochastic finite elements using a regression approach Comptes Rendus Mécanique, 336(6), pp. 518-523, 2008. DOI: 10.1016/j.crme.2008.02.013

[5] Blatman, G. and Sudret, B., An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabilistic Engineering Mechanics, 25(2), pp. 183-197, 2010. DOI: 10.1016/j.probengmech.2009.10.003

[6] Blatman, G. and Sudret, B., Adaptive sparse polynomial chaos expansion based on least angle regression, Journal Computational Physics, 230(6), pp. 2345-2367, 2011. DOI: 10.1016/j.jcp.2010.12.021

[7] Choi, S-K., Grandhi, R.V. and Canfield R.A., Reliability-based structural design. London: Springer, 2007. DOI: 10.1007/978-1-84628-445-8

[8] Christensen, R.M., Theory of viscoelasticity: An introduction, New York, Courier Corporation, 1982.

[9] Devroye, L., Non-Uniform Random Variate Generation, New York, Springer-Verlag, 1986.

[10] Doll, J.D. and Freeman D.L., Randomly exact methods. Science, 234(4782), pp. 1356-1360, 1986.

[11] Faming, L., Liu, C. and Carroll, R.J., Advanced markov chain monte carlo methods, United Kingdom John Wiley & Sons Ltd., 2010.

[12] Ferry, J.D., Viscoelastic properties of polymers, New York, Wiley, 1980.

[13] Ghanem, R.G. and Spanos, P.D., Stochastic finite elements: A spectral approach, New York, Springer-Verlag, 1999.

[14] Harr M.E., Reliability-based design in civil engineering, Dover Pubns, USA, 1997.

[15] Huang, S.P., Liang, B. and Phoon, K.K., Geotechnical probabilistic analysis by collocation-based stochastic response surface method, Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards, 3(2) pp. 75-86, 2009. DOI: 10.1080/17499510802571844

[16] Iman, R.L. and Conover, W.J., Small sample sensitivity analysis techniques for computer models, with an application to risk assessment. Communications in Statistics-Theory and Methods, 9(17), pp. 1749-1842, 1980.

[17] Isukapalli, S.S. Roy, A. and Georgopoulod, P.G., Stochastic response surface methods (SRSMs) for uncertainty propagation: Application to environmental and biological systems, Risk Analysis, 18(3) pp. 351-363, 1998.

[18] Isukapalli, S.S., Uncertainty analysis of transport-transformation models. PhD. Thesis, The State University of New Jersey, NJ, USA, 1999.

[19] Kewlani, G., Crawford, J. and Iagnemma, K., A polynomial chaos approach to the analysis of vehicle dynamics under uncertainty., Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 50(5) pp. 1-26, 2012. DOI: 10.1080/00423114.2011.639897

[20] Klir, G.J., The many faces of uncertainty, Elsevier Science, 1994.

[21] Le Maître, O.P. and Knio O.M., Spectral methods for uncertainty quantification: With applications to computational fluid dynamics, Springer, London, UK, 2010.

[22] Melchers, R.E., Structural reliability analysis and prediction, London, John Wiley and Sons, 1999.

[23] Neto, A.A.B., and Rosa, E., Parametric uncertainty analysis considering metrological aspects in the structural simulation in viscoelastic materials, LAJSS (Latin American Journal of Solids and Structures), 5(2008), pp. 75-95, 2008.

[24] Papoulis, A., Probability, random variables, and stochastic processes, New York, McGraw-Hill, 1991.

[25] Park, S.W. and Schapery R.A., Methods of interconversion between linear viscoelastic material functions. Part I - A numerical method based on Prony series, International Journal of Solids and Structures, 36(11), pp. 1653-1675, 1998. DOI: 10.1016/S0020-7683(98)00055-9

[26] Park, S.W. and Kim, Y.R., Interconversion between relaxation modulus and creep compliance for viscoelastic solids, Journal of Materials in Civil Engineering 11(1) pp. 76-82, 1999. DOI: 10.1061/(ASCE)0899-1561(1999)11:1(76), 76-82

[27] Phoon, K.K. and Huang, S.P., Uncertainty quantification using multi-dimensional hermite polynomials, ASCE, pp. 1-10, 2007. DOI: 10.1061/40914(233)12

[28] Schapery, R.A., On the characterization of nonlinear viscoelastic materials, Polymer Engineering and Science, 9(4), pp. 295-310, 1969.

[29] Srinivasan, R., Importance Sampling, New York, Springer-Verlag, 2002.

[30] Sudret, B. and Der Kiureghian, A., Stochastic finite elements and reliability: A state of the art report. Report UCB/SEMM-2000/08, University of California, Berkeley, USA. 2008.

[31] Sudret, B., Uncertainty propagation and sensitivity analysis in mechanical models contributions to structural reliability and stochastic spectral methods., Ph.D. Thesis, Université Blaise Pascal - Clermount II, Aubière, France, 2007.

[32] Tatang, M.A., Direct incorporation of uncertainty in chemical and environmental engineering systems, PhD Thesis, Massachusetts Institute of Technology, MA, USA, 1995.

[33] Tatang, M.A., Pan, W.W., Prinn, R.G. and McRae, G.J., An efficient methods for parametric uncertainty analysis of numerical geophysical model, Journal Geophysical Research Atmosphere 102(D18) pp. 21925-21932, 1997. DOI: 10.1029/97JD01654

[34] Wilhelm, F., Viscoelasticity, Second Ed. Revised, Springer-Verlag Berlin Heidelberg GmbH, 1975.

[35] Xiu, D., Fast numerical methods for stochastic computations: A review, Communications in Computational. Physics, 5(2-4), pp. 242-272, 2009.

[36] Xiu, D., Numerical methods for stochastic computations, New Jersey, Princeton University Press, USA, 2010.

[37] Xiu, D. and Hesthaven, J., High-order collocation methods for differential equations with random inputs, SIAM, Journal on Scientific Computing, 27(3), pp. 1118-1139, 2005. DOI: 10.1137/040615201

F. Evangelista Jr, received the BSc. Eng. in Civil Engineering in 2003, the MSc degree in Civil Engineering with emphasis in Transportation Infrastructure in 2006, both at the Universidade Federal do Ceará, Brazil. In 2011, he received his PhD degree in Civil Engineering at the University of Illinois at Urbana Champaign, USA. Since 2013, he has been professor at the Graduate Program of Structures and Civil Construction of the Universidade de Brasília. ORCID: 0000-0002-9353-1083

N.Afanador G. received the BSc. Eng. in Civil Engineering and graduate in mathematics and Physic in 1990, the MSc degree Civil Engineering with emphasis in structures at the Universidad of the Andes Colombia in 2008 and actually, he is studying the PhD degree in Structures at the University of Brasilia. Since 2003 to actually, he work for Francisco of Paula Santander University Ocaña in the department of civil engineering. ORCID: 0000-0001-5463-2036