Luis Eduardo Gallego Vega¹ y Oscar Germán Duarte Velasco²

¹Electrical Engineer. M.Sc., in Electrical Engineering. Ph.D., in Engineering, Universidad Nacional de Colombia, Bogotá, Colombia. Researcher, Grupo de Investigación PAAS, Universidad Nacional de Colomiba, Bogotá, Colombia. Assistant Professor, Department of electrical and electronic engineering, Universidad Nacional de Colombia, Bogotá, Colombia. lgallegov@unal.edu.co

ABSTRACT

This paper gives the results of research assessing and analysing local marginal prices in the national transmission grid as an alternative for analysing the effect of electric transmission constraints in the Colombian power market. This study compares the current one-bus model where a spot price is determined without considering transmission network constraints. It describes the modelling of the national transmission grid, power system operation and economic dispatch and a methodology for approaching the system´s electrical constraints and operational constraints. An analysis of local marginal prices for each operational zone in the Colombian power system is presented as a result of this modelling, as well as statistical modelling of congestion income.

Keywords: Local marginal price, bidding price, transmission constraint, power market, optimal power flow.

Received: may 29th 2009 Accepted: november 15th 2010

Introduction

The worldwide electric sector has been affected by several changes since the middle of the 1980s, mainly motivated by an increase in electric energy production efficiency. One of the main changes has been the transition to market structures by introducing competitiveness and private investments in sectors such as electric power generation. Such deregulation has been implemented for increasing efficiency and reducing energy prices, an improvement in power quality and major reliability in power systems (Joskow and Schmalensee, 1983).

Given this new market structure, generation companies tend to "internalise" most of the issues related to system operation in their bidding prices and the market energy price is obtained by matching the aggregated bidding curve against power demand. The market price for each hour is established by the variable cost of the last generation unit which was required to supply national power demand. However, it is expected that generation companies (GENCO) include their perception about transmission network constraints in their bidding prices. In fact, common problems such a trapped load or required generations to keep power sys-tem operation within secure ranges are conditions that may be exploited by GENCOs to influence power market prices and obtain higher profits, given their strategic location in the power transmission network.

In this regard, the international community has faced this problem from different perspectives including game-theory, large-scale optimisation tools, microeconomic theory and even agent´s computational economics. The most popular approaches deal with equilibrium models in which the solution requires that none of the agents have incentives for unilaterally deviating from their chosen strategies, normally known as a Nash Equilibrium (Hobbs, 2001).

Cournot models are the most popular equilibrium models, whose more sophisticated versions implement the effect of transmission networks on agent´s market power. The mathematical back-ground is mainly based on mixed complementary problems (MCP) in this type of model, with some algorithms already implemented in software such as GAMS. Some of the most interesting work in this area may be found in (Hobbs et al., 2000; Daxhelet and Smeers, 2001; Ventosa et al., 2000).

Cournot models have been focused on improving numerical solutions for obtaining Nash equilibrium in recent years as well as a more suitable representation of network constraints and power demand. Contreras and Klusch (2004) have proposed a numerical algorithm for solving Cournot models considering coupled constraints among GENCOs, where the set of actions available to any GENCO is limited by the action of the other competitors. Hobbs and Pang (2007) have proposed a model using piece-wise linear functions to model power demand and network constraints, including some variables from competitors in the optimisation problem.

In the case of Colombia, there is no evidence of large-scale studies for determining the effect of network constraints on energy prices including explicit modelling of the power transmission sys-tem. On the contrary, studies to date have analysed the effect of network constraints in a more descriptive way, trying to estimate GENCO behaviour in each power system operating area regarding their bidding strategies but without modelling the optimisation of power flows in each area. The case of the Colombian spot market has been studied by focusing on the commercial impact of some technical aspects of the national power grid (NTG) (Jaramillo, 2002; Jaramillo and Sanint, 2002), particularly regarding network constraints related to voltage and power which may prevent the Colombian power market becoming a competitive market. This analysis was based on classic game theory using typical payoff matrix representation to assess the set of optimal bidding strategies. A concept called individual agent restriction capacity (IARC) tried to measure the bidding ability of any GENCO in any operation area when network constraints are present. This parameter was calculated by comparing power demand in any area to power inflow and the power capacity of competitors in the same area. A low IARC value indicated that none of the GENCOs in the area were strictly required to supply local demand, given that it might have been covered by any other GENCO and therefore, no market power could be exercised. Campuzano and Smith (2002) analysed Colombian GENCOs´ market power for establishing the limits on ownership of electrical generation resources that provide a competitive power market. The research used classic game theory and system dynamics. System dynamics are simulated by using a four-year period with a monthlybasis resolution and the market power criterion of the frequency in which any GENCO is required to attend local power demand in the area allowing market price to be fixed. The modelling of electric system operation includes several modules such as hydrology, power demand, installed capacity disaggregated by technology and bidding price module aggregated by generation technology on a monthly-basis.

These works have been motivated by current Colombian market structure in which market prices are calculated by assuming a onebus power system model having enough transmission capacity to neglect the effect of transmission constraints on market prices. Unlike previous work in this area, this paper considers the explicit modelling of the NTG to represent the effect of network constraints on calculating spot market prices. This effect is reflected in calculating local marginal prices (LMP) for each operation area of the Colombian power system, quantifying the cost of supplying one more unit of power demanded in each of the gene-ration buses and considering optimal power flow (OPF) against peak demand conditions.

The bidding prices data in this work, on which OPF algorithms are based, were provided by XM Expertos en Mercados S.A, which is the company responsible for administering the Colombian power market. This information was provided as part of a research project called, "Modelling electric energy supply pattern," sponsored by the Universidad Nacional de Colombia.

On the other hand, due to bidding price confidentiality, this analysis is based on bidding information available for 2001 to 2004 which is stored in the Colombian power market database (NEON).

Modelling the national transmission power grid

This section describes the main NTG characteristics and the methodologie associated with data processing, adapting the soft-ware tool used for simulations, identifying the operation areas in the transmission system and treatment of power demand in the implemented model. Dispatch-price related models used for simulating Colombian power system pattern on an hourly-basis as well as processing electric network constraints considered are al-so explained.

The explicit modelling of the NTG was implemented by following the Transmission Expansion Reference Plan 2006-2020 (UPME, 2006) which considered all generation plants and trans-mission lines. This information was provided in tables describing each element in the power system; therefore, a database tool using MySQL server was developed to obtain a matrix representtation of system connectivity allowing OPF simulation.

On the other hand, given the number of buses associated with the Colombian power system, simulation was not possible in an academic version of available power system simulators. Moreover, systematic, iterative and completely modifiable simulation such as that intended in this study is not easily implemented in any comercial simulation platform. Based on the above, MAT-POWER (Murillo and Zimmermann, 2007) was the simulation tool finally chosen which is a MATLAB-based package for resolving OPFs. This package has the advantage that it may be adapted to any other simulation environment developed in the same programming language, given that its input parameters are conceived as matrix representations of power systems. This feature allows systematic modification of some parameter values in input matrices and consequently, iterative simulation of a great number of cases in different demand scenarios, bidding, power sys-tem setup, etc. Some variations in the original MATPOWER code were necessary for modifying bidding strategies, power demand in each bus and loading capacity in transmission lines sequentially connecting Colombian power system operation areas.

The modelled buses represent bus-bar substations neglecting the buses associated with interruption devices. National power demand was associated with 259 buses with both a particular power factor and a particular distribution factor. This information was provided by UPME and is summarised in Table 1.

Implementing generation plants and identifying operation areas

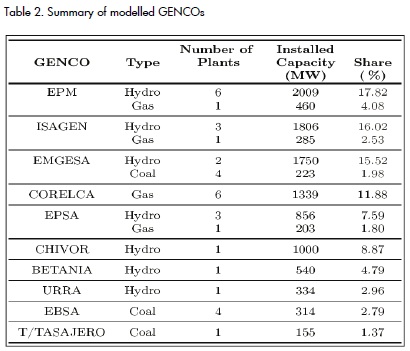
The set of modelled generation plants was selected as a result of an analysis of share of both installed capacity ownership and energy generation during hourly economic dispatch. The number of representative generation units per GENCO was chosen according to these plants´ share of total GENCO energy generation. Thirty-five generation plants were modelled, representing 91% of installed capacity. The remaining 9% were mostly minor plants which are not obliged to bid in the Colombian power market. These 35 plants are grouped into 10 GENCOs, which is a very representative sample of the Colombian power system.

A summary of the GENCOs modelled is shown in Table 2.

On the other hand, Colombian power system operation is based on the concept of operating areas, determining limits on importing and exporting energy between them. An operating area is defined as a set of connection assets, generation resources and power demand levels which present any electrical constraint (CREG 062,2000). This research follows Colombian independent system operator(ISO) area classification (XM S.A.). Therefore, the Colombian power system is divided into six areas: Caribbean, Caribbean 2 Eastern, South-western, Antioquia-San Carlos (ASC) and Northeastern area. Consequently, each power system bus was assigned to the correspondent operation area.

A first analysis in each operation area showed that GENCO share in most areas behaves as a duopoly. This structure may suggest a possible game theory formulation for each operation area.

The economic dispatch problem

The economic dispatch problem was formulated as the solution to an OPF on the NTG. Such OPFs were based on the bidding prices submitted by each generation unit considered. DC-OPFs and ACOPFs were implemented and compared, regarding software simulation tool performance.

Regarding AC-OPFs, some instability problems in algorithm convergence were found, given the great number of variables involved in optimisation problem constraints (bus voltage, active and reactive power limits in transmission lines, operation limits in generation plants, etc.). Moreover, a high computational burden was demanded during the testing of this type of power flow, resulting in solving times lasting minutes for just one particular power flow. Such resolving times were not so appealing for this work in which thousands of power flows had to be resolved for estimating the effect of electric network constraints.

Unlike AC-OPFs, DC-OPFs presented less convergence-related problems and their solutions were much faster and more efficient (seconds), provided a software tool with suitable treatment of sparse matrices was available. Some additional libraries based on interior point methods for solving linear programming problems were used (Mészáros, 1996). It should be remembered that this type of dispatch neglects transmission lines´ active power losses and the reactive power flows necessary to hold voltage buses in operating ranges. However, such type of reactive power flows are not tradable over wide operating areas due to transmission lines´ high reactive power losses (Kirschen and Strbac, 2005). According to the current market structure in Colombia, this type of power is not tradable, although in the short-term it might be compensable as an ancillary service. Based on the above mentioned, economic dispatch in the NTG was represented by the solution of a DC-OPF stated as the following optimisation problem:

Now, given that Colombian economic dispatch follows a scheme based on bidding prices submitted by GENCOs, costs Ci(Pgi) were represented by linear functions whose slopes matched the submitted bidding price of each generation unit. The real economic dispatch pattern was simulated based on operating limits for each transmission line and each NTG generation unit. This modelling only considered electrical constraints (thermal limits) and not necessarily operating constraints (stability, frequency regulation, reactive compensation, etc). Nevertheless, the following section presents a methodology for adjusting DCOPF results, considering operating constraints, as an attempt to relax the assumptions considered by the complete ACOPF problem and also keep the computational burden of simulations within reasonable ranges.

Operation constraint approach methodology

Operating constraints may imply that thermal limits are not necessarily reached for satisfying some power system safety or reliability requirement. For instance, a transmission line is not necessarily used to its maximum capacity during hourly power system operation. A comparison between simulated DCOPFs and real energy dispatch observed in the Colombian power system 2001-2004 was thus carried out.

The first part of the analysis consisted of reproducing NTG peak hour economic dispatch (DC optimal flows during high congestion hours in the transmission system) based on both bidding prices submitted by each generation unit and national power demand (NEON database). This analysis was focused on the active power flows of the transmission lines joining the six Colombian operating areas (Colombian interties lines), defining exportation and importation limits amongst them. For the case of the Colombian power system, a total of 40 transmission lines were considered as interties li-nes. Given this criterion, a statistical analysis was made of the 50%, 90% and 95% percentiles for active power flows in these lines.

The second part of the analysis consisted of simulating and analysing power flows in the interties lines during real power system operation. It should be clarified that this data is not available in any database and this information is considered as confidential. This problem was solved by simulating AC power flows based on real generation plant generation available in the NEON database. In other words, real energy generation during peak power system hours were taken as an initial condition to run AC power flows aimed at estimating power flows in interties lines. As a result of this analysis, a statistical characterisation of the 50%, 90% and 95% percenttiles for t power flow values in these lines was compared to the results of the first part (DCOPFs).

As mentioned before, the strategy was focused on comparing 90% percentiles, comparing a situation where only electrical constraints were considered to one where electrical and operative constraints were considered. This comparison showed the pattern of maximum required power flows in interties lines, allowing maximum values to be found (considering electrical and operating constraints) which might have been less than those considered in the DCOPF (thermal limits). In such specific cases, a redefinition of electrical constraints may represent an approach to both electrical and operational constraints, with no effect on the algorithms´ computational burden.

The results for each of the 40 interties lines have already been published (Gallego, 2008). However, it is important to highlight that this proposed redefinition was effective in almost half of the interties lines (19 lines). Such redefinition resulted in less error in estimating power and energy generated by each operation area when compared to the real power market data, reducing 12% error using DCOPF to 3-4% using modified DCOPF (adjusted electrical constraints). This improvement was achieved without increasing algorithm solving time.

Local marginal prices and congestion income in the national transmission grid

This section presents analysis related to the costs associated with NTG constraints, understood as being total overcost obtained when limits in energy transmission amongst operation areas are present. A characterisation of the average local marginal price for each operation area is presented.

Local marginal price methodology

Given that the OPF consists of an optimisation problem, sensitivity analysis was possible, understood as assessment of variation in objective function given that some constraints were "relaxed." The concept of reduced cost emerged as a result of such relaxation, indicating how much variation occurs in objective function when limit on any constraint is increased or decreased (Rau, 2003). In the case of a DCOPF, this reduced cost indicates the variation in system operation cost when a generation plant increases or decreases its maximum generation capacity in 1 MW. This concept is fundamental for understanding the meaning of LMP.

The objective of LMP assessment is to find the marginal cost of supplying one more unit of demand (1 more MW or MWh) in a specific power system bus. This situation (1 more unit of demand) implies that less generation is now available to supply the rest of the power demand (by 1 less unit of demand), which can be interpretted as a reduction in power generation capacity of the generation plant attending this particular bus and consequently, produces va riation in objective function (reduced cost). Moreover, this additional unit of demand will be supplied by this generation plant at its bidding price. Therefore, the marginal cost of supplying such additional unit of demand will be the cost of reducing generation capacity limit in the same unit (reduced cost) plus the cost at which this additionnal unit is supplied by this specific generation plant (bidding price). It should be noted that the reduced cost will have a value different to zero only when the associated constraint is bound, indicating that this generation unit is strictly necessary to supply the demand. On the contrary, a generation plant which i not necessary for supplying demand will not be bound and, therefore, its reduced cost is equal to zero.

On the other hand, the effect of constraints on the relationship between bidding prices and reduced costs should be distinguished. There is an inverse and totally linear relation between reduced costs and bidding prices in a scenario with no transmission constraints, implying that the lower the bidding price, the higher the reduced costs and, consequently, the bigger the impact on power system cost. This relationship is similar to so-called ideal dispatch in which the spot price is calculated in the Colombian power market

To illustrate this idea, Figure 1 shows the relationship between bidding prices and reduced costs for a particular case of hourly economic dispatch. This dispatch was obtained by simulating a DCOPF considering infinite transmission capacity (no constraints) in Colombian power system transmission lines. Otherwise, in the case of the presence of transmission constraints, such inverse, linear relationship is no longer valid and is now completely deformed, implying that a generation plant having a lower bidding price does not necessarily have higher reduced cost (i.e. a plant with a lower bidding price does not necessarily have an impact on system operation cost in a greater manner than that having a higher bidding price). This effect is shown for the same case of hourly dispatch i Figure 1, considering transmission network constraints. These non-linearities are the ones suggesting analysis using a multibus model, which means that LMPs are more suitable, given that some constraints are binding in the Colombian powe system, instead of a one-bus model like the one used in current Colombian power market structure.

Characterising LMPs in the national transmission grid

Economic dispatch for peak hour based on both peak demand and real bidding prices submitted by each generation plant was carried out for each day (2001-2004) for characterising each NTG operation area. A different LMP was obtained as a result of this analysis for each dispatch and for each of the 178 generation buses, which were averaged among the buses belonging to a specific operation area. The marginal cost of supplying an additional unit of demand in each operation area was obtained. This average reflected the pattern of each operation area and was not intended to be the clearance price in each area for compensable purposes.

From this point of view, Figure 2 and Figure 3 show average LMP pattern in each operation area for power system peak hour. It should be stressed that data shown in Figure 3 represents LMP pattern during 2004; however, the final calculated LMPs includes the pattern during the complete period: 2001-2004.

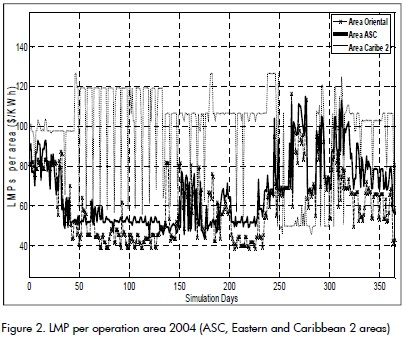
The operation areas illustrated in Figure 2 present average LMP lower than that shown in Figure 3. These results are illustrated in Table 3, where Eastern and ASC operation areas show that the marginal cost of supplying an additional unit of demand was lower than that obtained in Caribbean, Caribbean 2 and South-western operation areas. This result may be explained by both the great share of hydro portfolios in the first operation area and the greater "meshing" in power transmission system in this area of the power system.

As an important conclusion, differentiated LMPs amongst operation areas suggests that transmission constraints have the effect of increasing system operation costs. The natural question that may arise from such statement is how much are these overcosts? The following section deals with this particular issue.

Methodology for calculating network constraint costs

The cost of calculating network constraints was based on the differrence between operation costs in a transmission-constrained scenario and an infinite transmission capacity scenario. In particular,hourly dispatches for the peak hour considering real demand and real bidding prices were considered. As a result overcosts in ($/KWh) were obtained which were represented by empirical statistical distribution for system peak hour. Again, peak hour was selected because transmission network is more required and demanded during this period.

The results of constraint costs are presented in the form of empirical probability distributions. However, the most interesting result was its unimodal and asymmetrical pattern which could be fitted to a parametrical probability distribution. The result was a locationscale Student-t distribution with scale parameter ⌋, location parameter μ, and v degrees of freedom. In other words, constraints costs were transformed to empirical probability distribution by taking original network constraints (Cr) and appling the following equation:

Where Ctrans follows Student-t probability distribution with 2.35 degrees of freedom. This fitting is shown in Figure 4.

Validating the implemented model

Simulated spot prices and real spot prices for system peak hour were compared for verifying the model´s validation. Likewise, system cost operations were also calculated. Figure 5 shows a comparison between real spot prices, simulated spot prices and system operation costs. Very good correlation was found between real spot prices and simulated spot prices, given that they followed the same trend. However, several of the model´s limitations explain some differences with real spot prices.

First, some technical characteristics of the generating plants were revisited throughout the process known as ideal dispatch such as starting and stop ramps, minimum and maximum power limits and times required to reach stability in the power generated, which may cause the presence of forced generations due to generation plant technical inflexibility.

These inflexible or forced generations were analysed on the data stored in the NEON database for determining the magnitude for each hour. The curve obtained in Figure 5 shows the average magnitude of inflexibilities per unit of daily peak power demand for each hour. An empirical probability distribution for this variable at each hour was obtained for the Colombian power system. Therefore, generating these inflexibility values followed a random pattern based on the empirical probability distributions obtained. The random generation was based on a process called "roulette wheel," extensively used in some heuristics such as genetic algorithms(Holland, 1986).

The exact simulation of these inflexibilities for each generating plant in the Colombian power system is a very complex task given that it requires complete information about these plants´ technical operation details. This information is extremely difficult to find because it is commonly treated as being confidential. However, the probabilistic representation of inflexibilities led to very good correlations between real and simulated spot prices (Figure 6). Therefore,this representation was considered acceptable and sui-table for the purposes of this work. Minimum and maximum power ranges were considered inflexibility parameters for each generating plant, which are also one of the constraints involved in formulating the implemented DCOPFs models.

Conclusions

The explicit implementation of the national power grid in a totally flexible and configurable tool is a very meaningful contribution to simulating the Colombian power market. This implementation led to using this tool as an experimental lab, systematically simulating economic dispatches with total control of demand profiles, bidding strategies and even power system set up. This task is not easily achieved with a commercial software package.

On the other hand, such implementation led to more accurate modelling of operating conditions in the Colombian power system, particularly of transmission network constraints which are traditionally neglected in most studies about the Colombian power market due to the complexity involved in a large-scale power system.

The methodology developed for adjusting DCOPFs led to more accurate assessment of electrical constraints and operational constraints, keeping the computational burden within reasonable ranges which is a critical issue in the work developed in this paper.

Some issues about Colombian power market particularities might be stated as general conclusions. The simulations led to finding that network constraint costs might be modelled as empirical probability distribution during power sys-tem peak hours. This distribution was location-scale Student-t pro-bability distribution whose regularity could be useful in designing new schemes of compensating transmission network constraints.

On the other hand, the power system´s multibus property must be emphasised in the Colombian power market structure. As a result of the achieved simulations, great differences were found in average LMP amongst different operational areas, confirming the Colombian power system´s multibus property. In fact, if the simulations had shown a very similar pattern for the marginal costs of supplying an additional unit of demand in each operation area, a one-bus model might be considered a suitable model for representing the Colombian power market.

Unfortunately, this is not the case in Colombia, as a structural problem undeniable exists in the current power market,considering a one-bus model and not re-presenting the effect of network constraints using LMPs but instead using compensation formulas such as positive and negative recon-ciliation. In other words, the current compensating formulas com-paring bidding prices to spot prices and establishing a compensa-ting price between both prices (in some cases as a simple average) do not accurately represent the effect of network constraints, be-cause this formulation lacks any technical background. The fact that LMPs were different in each operation area may suggest alternative market designs where clearing prices are based on each operation area´s LMP. This alternative proposal would more accurately represent the effect of network constraints on system operational cost as well as congestion income by contrast with tthe current structure where simple averages between bidding and spot prices do not accurately represent the marginal cost of supplying one more unit of demand in a specific bus in the Colombian power system.

References

Campuzano, C., Determinación de poder de mercado para los generadores en el sector eléctrico colombiano., Tesis de Maestría Universidad Nacional de Colombia - Sede Medellín, 2002.

Contreras, J., Klusch, M., Numerical solutions to nash-cournot equilibria in coupled constraint electricity markets., IEEE Transactions on Power Systems, 19(1), 2004, pp. 195-206.

Daxhelet, O., Smeers, Y., Variational Inequality Models of Restructured Electricity Systems, Vol. Complementarity: Applications, Algorithms and Extensions, Kluwer Academic Publishers, 2001.

Gallego, L. E., Modelamiento del comportamiento de la oferta de la energía eléctrica en el mercado colombiano., PhD thesis, Universidad Nacional de Colombia, 2008.

Hobbs, B., Linear complementarity models of nash-cournot competition in bilateral and poolco power markets., IEEE Transactions on Power Systems, 16(2), 2001, pp. 194-202.

Hobbs, B., Metzler, C., Pang, J. S,. Calculating equilibria in imperfectly competitive power markets: An mpec approach., IEEE Transactions on Power Systems, 15, 2000, pp. 638-645.

Hobbs, B., Pang, J., Nash-cournot equilibria in electric power markets with piecewise linear demand functions and joint constraints., operations Research, 55, 2007, pp. 113-127.

Holland, J.,), Adaption in Natural and Artificial Systems., University of Michigan Press., 1975.

Holland, J., Induction: processes of inference, learning and discovery., MIT Press, 1986.,

Jaramillo, A., La bolsa de energía eléctrica a la luz de la teoría de juegos., Tesis de Maestría, Universidad Nacional de Colombia Sede Medellin, Facultad de Ciencias Humanas, Maestría en Economía Energética y de los Recursos Naturales, 2002.

Jaramillo, A., Sanint, E., Las restricciones en el mercado eléctrico colombiano., Revista Energética, 25, 2002, pp. 9-18.

Joskow, P., Schmalensee R., Markets for power: An Analysis of Electrical Utility Deregulation., The MIT Press, 1983.

Kirschen, D., Goran Strbac., Fundamentals of Power System Economics., Wiley, 2005.

Mészáros, Cs.., Fast cholesky factorization for interior point methods of linear programming., Computers & Mathematics with Applications, 31(4/5), 1996, pp. 49-51.

Rau, N., Optimization principles Practical applications to the operation and markets of the electric power industry., IEEE Press. 2003.

Murillo, C., Zimmermann, R., Matpower 3.2., 2007. http://www.pserc.cornell.edu

UPME., Plan de Expansión de Referencia Generación - Transmisión, 2006 - 2020., Unidad de Planeación Minero Energética, 2006.

Ventosa, M., Rivier, M., Ramos, A., An mcp approach for hydrothermal coordination in deregulated power markets., in IEEE - PES Summer Meeting, Seattle, 2000.