Liliana Camargo ¹ y Jairo Duque ²

¹ Matemática, Universidad del Valle, Cali, Colombia. Universidad del Valle. lilicaz85@gmail.com.

² Dr. rer. nat., Universidad del Valle, Cali, Colombia. jjduque@univalle.edu.co

RESUMEN

En este trabajo presentamos la implementación de un método de elementos finitos combinado con la aplicación Dirichlet-to-Neumann (D†N), obtenida en términos de series de Fourier, para estudiar la existencia de soluciones de un problema exterior que proviene de la teoría de elasticidad lineal incompresible bidimensional. Finalmente, se presenta un método numérico que demuestra la precisión de nuestra aplicación D†N, puesto que sólo se necesitan unos cuantos términos de la serie de Fourier para obtener una buena aproximación de la solución. Para la discretización del problema se emplea el elemento estable Taylor-Hood.

Palabras clave: método de elementos finitos mixto, elemento Taylor-Hood, técnica D†N, elasticidad lineal, condición infsup.

Recibido: septiembre 4 de 2009

Aceptado: noviembre 15 de 2010

Introducción

En este trabajo se explica un procedimiento para estudiar la aproximación de Galerkin de un material incompresible en un dominio exterior no acotado Ω. El procedimiento emplea la aplicación Dirichlet-to-Neumann (D†N) (Han y Bao, 1997; Gatica, Gatica y Stephan, 2003; Kako y Touda, 2004), que consiste en introducir una frontera artificial dibujando en Ω un círculo Γ_R en R² de radio R. Entonces Ω se divide en la parte acotada Ω_i y la no acotada Ω_R. Para resolver el problema en el dominio acotado Ω_i se dan condiciones de frontera exactas y aproximadas sobre la frontera artificial Γ_R (Figura 1).

Figura 1. Dominio Ω = Ω_i; ∪ Ω_R y frontera artificial Γ_R.

Sea Ω С R² un dominio no acotado y simplemente conexo con frontera Lipschitz continua Γ. Teniendo en cuenta las condiciones de frontera tipo Dirichlet dadas sobre Γ se define el espacio . Así, el problema de elasticidad lineal por resolver consiste en encontrar (u,p) ∈ tal que:

Aquí u: Ω → R representa el desplazamiento y p es la presión del material en cada punto x:= (x₁,x₂ )^T ∈ Ω por el efecto de la fuerza externa ƒ, µ > 0 es la constante de Lamé y ε(u) representa el tensor de esfuerzos de componentes para i, j =1,2. De este material suponemos válida la relación tensiónesfuerzo para pequeñas deformaciones, tal como se discute en Necas (1986); véanse también Necas (1981) y Zeidler (1988). En este trabajo suponemos que la fuerza ƒ tiene soporte compacto y que está contenida en la región Ω_i.

Sean espacios dotados con las normas de L² (Ω) y H¹(Ω) respectivamente. Entonces, siguiendo el procedimiento estándar de integración por partes, se llega a la siguiente formulación variacional del problema (1):

Nótese que este problema está definido en el dominio no acotado Ω y Ω_i es el dominio computacional para nuestro método de elementos finitos, que se obtiene al introducir la frontera artificial Γ_R. Entonces es necesario deducir la formulación variacional del problema (1) en Ω_i; nuevamente mediante integración por partes, y teniendo en cuenta que para el tensor distorsión σ (u, p):= 2 με(u) - pI , donde I es la matriz identidad de orden 2, se tiene que – div (σ(u, p) = 2μ div ε (u ) + grad p, y a partir de esto se obtiene la formulación débil:

El análisis se concentra ahora en la integral de frontera, Nuestro objetivo es obtener una expresión para el tensor σ (u, p) a lo largo de la frontera artificial Γ_R. Consideremos entonces la siguiente descomposición del desplazamiento u, en el dominio no acotado Ω_R =

siendo G₁ , G₂ y W funciones armónicas que determinaremos más adelante. En particular, las funciones G_j satisfacen el siguiente problema de valores de frontera:

Nótese que los valores de G_j y u_j coinciden a lo largo de Γ_R. Usando el método de separación de variables obtenemos las siguientes representaciones de G_j en términos de los coeficientes de Fourier:

donde los coeficientes a_n,b_n y d_n están dados por:

Usando la condición div (u)= 0 y la representación (3) se obtiene , y de aquí

Análogamente, usando la ecuación de balance en Ω_R, grad p = 2μ div ε(u), obtenemos grad y de aquí se deduce que . Ahora estamos en condiciones de calcular a lo largo de Γ_R. Recordando que los valores de u_j y G_j coinciden sobre Γ_R, y que la presión p se conoce en términos de W se obtiene:

donde

que sólo depende de la variación de u a lo largo de Γ_R. El operador T(u) se conoce como aplicación Dirichlet to Neumann. Obsérvese que el problema variacional (2) es la formulación débil del problema:

Existencia y unicidad de soluciones

Consideremos las formas bilineales y el funcional lineal F: X→ R definidos mediante:

y respectivamente. Entonces el problema variacional (2) consiste en encontrar (u,p) ∈ X x M tal que

La demostración de existencia y unicidad de este problema se basa en el teorema de Brezzi, puesto que la forma A(u,v) + A₀ (u,v) es continua y coerciva, y el operador B satisface la condición inf-sup (Han y Bao, 1997; Camargo, 2008).

Método de elementos finitos

El método de elementos finitos que presentamos en este trabajo no aproxima la solución del problema (4), sino la solución del problema que se obtiene truncando la serie de Fourier, en términos de la cual está definido el operador T(u). Al reemplazar por para un valor entero de N, obtenemos el problema aproximado: encontrar ( u_N , p_N ) ∈ X x M tal que

con j = 1, 2. El estudio de existencia y unicidad del problema (5) es análogo al del problema exacto (Han y Bao, 1997; Camargo, 2008). Además, se tiene el siguiente estimativo para el error de la aproximación ( u_N , p_N ).

Teorema 1. Sean las soluciones de los problemas variacionales (4) y (5), respectivamente. Además, suponga con m ∈ Z. Entonces el siguiente estimativo del error se cumple:

donde C es una constante independiente de N y m.

Ahora, sean X_h С X y M_h С M los espacios de elementos finitos correspondientes al elemento Taylor-Hood, (Brezzi, 1991), y denotemos por T_h la partición regular del dominio Ω_i, en elementos triangulares curvilíneos T de diámetro h_t , donde . Entonces,el método de elementos finitos para aproximar el problema (5)con-siste en encontrar tal que

Nótese que el elemento Taylor-Hood satisface la condición inf-sup (Brezzi, 1991) y nuevamente por el teorema de Brezzi es inmediata la existencia de una única solución para (6).

Teorema 2. Suponga que es la solución del problema (4) y es la solución del problema (6(, así que el siguiente estimativo de error se cumple:

donde C es una constante independiente de h y N.

Demostración. Sea la solución del problema (5)para cualquier entero N ≥0 y consideremos los errores y empleando la técnica estándar del método de elementos finitos mixto se sigue que existe independiente de N y el diámetro h de la triangulación de Ω_i tal que:

Además,

y empleando (7) se sigue que

lo que concluye la demostración del teorema.

Implementación de la técnica D†N

Sea Ω el dominio no acotado la circunferencia de radio R = 2 y

donde y . Entonces, es la única solución del siguiente problema de valores de frontera:

Dado n ∈ N, una partición uniforme de la parametrización del círculo definida poy y (t)= R(cos (t), sen(t))^T. Entonces denotamos con Ω_h la región anular acotada por (cos(t),sen (t)) Γ= y la línea poligonal cerrada Γ_h con vértices y sea T_h una triangulación regular de Ω_h con triángulos T de diámetro h_T tal que .

Ahora consideramos el triángulo canónico con vértices como un triángulo de referencia , e introducimos la familia de transformaciones afines biyectivas tal que para todo T ∈ T_h. Es bien conocido que 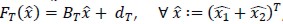, donde y depende de los vértices del triángulo T. Además, dado un entero l > 0 y un subconjunto S of R², denotamos con P_i( S) el espacio de polinomios en dos variables definidos en S de grado total a lo más l.

Con el fin de especificar X_h y M_h tomamos

Entonces discretizamos X usando

      Figura 2. Secuencia T_o,h, … T_3,h de mallas usadas en la implementación.

y M con

Los espacios X_h y M_h constituyen los subespacios de elementos finitos Hood y Taylor más sencillos que satisfacen la condición inf-sup. En nuestra implementación usamos varias triangulaciones. Nosotros arrancamos la experimentación numérica con la malla inicial T_o,h con 26 elementos. Cada malla refinada uniformemente T_1,h ,…,T_3,h se generó dividiendo cada triángulo en cuatro más pequeños. El resultado se puede observar en la figura 2.

Tabla 1. Grados de libertad (Gdl) y norma L²; de los errores cuando N = 7.

La tabla 1 muestra la norma L² de los errores u - u_h,N¸ p - p_{h, N} cuando N = 7 para las mallas T_o,h,…,T_3,h

Tabla 2. Norma L² de los errores para T_3,h cuando N = 0, 1, 3, 5, 7.

La tabla 2 muestra la norma L² de los errores u - u_h,N¸ p - p_{h, N}; para la malla T_3,h

La figura 3 muestra los valores de y p_h para todas las mallas y N = 7. Como muestra la figura, N = 7 produce buena aproximaci&loacute;n y pocos términos se necesitan en la forma bilineal A₀ para obtener resultados precisos.

Figura 3. y p para las mallas T_o,h,…,T_1,h y T_3,h cuando N = 7.

Conclusiones

En este artículo se usa una aplicación D†N para aproximar la solución de un problema exterior no acotado. Con este fin se introduce una frontera artificial en el dominio computacional acotado, en el que se aproxima la solución usando el método de elementos finitos.

Específicamente, se implementa el elemento Taylor-Hood, el cual se define en términos de una serie de Fourier sobre la frontera artificial. Los cálculos numéricos muestran que truncando la serie en siete términos se logra una buena convergencia. Sin embargo, en nuestra aproximación el operador de frontera tiene asociada una matriz de rigidez densa y se usaron precondicionadores especiales para obtener buena convergencia.

Bibliografía

Brezzi F., Fortin M., Mixed and hybrid finite element methods.,Springer-Verlag, 1991.

Camargo, L., Aplicación D†N-FEM a un problema elástico lineal.,BSc Mathematics thesis, Universidad del Valle, 2008.

Gatica G. N., Gatica L. F., Stephan E. P., A FEM–D†N formulation for a non-linear exterior problem in incompressible elasticity., Mathematical Methods in the Applied sciences, 26, 2003, pp. 151–170.

Han H., Bao W., The artificial boundary conditions for incompressible materials on an unbounded domain.,Numerische Mathematik, 1997.

Kako T., Touda K., Numerical simulation of voice generation based on finite element method in unbounded region.,Department of computer science, Japan, 2004.

Necas, J. Introduction to the theory of nonlinear elliptic equations., John Wiley & Sons, 1986.

Necas, J., Hlavacek, I., Mathematical theory of elastic and elastoplastic bodies: an introduction., Elsevier scientific publishing company, 1981.

Zeidler, E., Nonlinear functional analysis and its applications IV., Springer-Verlag, New York, 1988.