Antonio H. Escobar Z.¹, Ramón A. Gallego R.², Rubén A. Romero L³.

¹ Ph.D., Universidad Estadual P aulista, Brazil. Professor, Univer sidad Tecnológica de Pereira, Colombia. aescobar@utp.edu.co

² Ph.D., Universidad Est adual de Campinas, Brazil. Professor, Universidad Tecnológica de Pereira, Colombia. ragr@utp.edu.co

³ M.Sc. and Ph.D., Universidad Estadual de Campinas, Brazil. Professor, DEEFEIS-UNESP, Brazil. ruben@dee.feis.unesp.

ABSTRACT

This paper analyses the impact of choosing good initial populations for genetic algorithms regarding convergence speed and final solution quality. Test problems were taken from complex electricity distribution network expansion planning. Constructive heuristic algorithms were used to generate good initial populations, particularly those used in resolving transmission network expansion planning. The results were compared to those found by a genetic algorithm with random initial populations. The results showed that an efficiently generated initial population led to better solutions being found in less time when applied to low complexity electricity distribution networks and better quality solutions for highly complex networks when compared to a genetic algorithm using random initial populations.

Keywords: electricity distribution network expansion planning, genetic algorithm, constructive heuristic algorithm, met heuristics, initial population.

Received: Feuary 01th 2010. Accepted: Feuary 7th 2011

Introduction

A planning problem’s solution specifies where, how many and when new equipment must be installed in an electricity distribution system so that it operates adequately within a specified planning scenario. Static planning considers only one planning horizon and determines the number of circuits which should be added to each anch of an electricity distribution system. Mathematical models become more complex if different operation modes are taken into account such as multistage planning, security conditions, operation conditions in a competitive market which can be incorporated in a model. Although this paper only deals with static planning, it can be applied to more complex modelling situations.

The DC mode has been used to represent an electricity distribution network, since only transmission network active power planning is considered; it should be said that this is considered ideal for long-term planning. The DC model formulates optimising the planning of transmission system expansion. It is equivalent to a mixed-integer non-linear programming problem. Complexity increases due to the existence of a large number of local optimum solutions. Also, the number of solutions grows exponentially as a system gets larger.

Many techniques have been proposed in the field literature for resolving mathematically modelled planning problems. The following references (Garver, 1970; Villasana,1985; Gallego, 1998; Gallego, 2000; Haffner, 2001; Da Silva, 2000) show techniques corresponding to classical optimisation, whereas(Villasana, 1985; Monticelli, 1982; Pereira, 1985) used heuristic techniques and (Gallego, 1998a; Gallego, 1998b; Gallego, 2000; Davila,2000; Escobar, 2004; Romero, 2007) used met heuristic techniques. Met heuristic techniques have been dominant in relation to efficiency and solution quality when planning involves large size and complexity. A more detailed analysis of transmission system expansion planning and optimisation techniques can be found in (Romero, 2002; Latorre, 2003; Lee, 2006).

This paper specifically analyses the impact of efficient initial populations on convergence speed and solution quality by using a genetic algorithm. Such aspects are tested regarding transmission planning on large-size and highly-complex distribution systems and the results are compared with those obtained by a genetic algorithm with random initial population.

This issue has been explored because of the need for documenting the experimental conjecture that good initial populations have a tremendous impact on met heuristic technique performance in highly complex systems, at least in planning (Gallego, 1998a; Gallego, 1998b). The topic has emerged in the literature (Maaranen, 2007) regarding the relevance of choosing good initial populations and there have been new theoretical developments on met heuristics in which good initial populations have been recognised as crucial (Hansen, 2003).

In (Maaranen, 2007) the impact of different methods for choosing initial populations was determined for a general genetic algorithm, without any knowledge of the specific problem. Initial populations were generated using 4 different methods and results were compared to uniform coverage and genetic diversity in convergence and final objective function value. The four techniques involved slight differences. Initial configuration was a key factor in convergence speed and differences in early generation became important in solving many real-life problems where evaluation of objective functions may have required timeconsuming simulations and the optimisation algorithm may have had to be stopped prematurely. It was made clear (through an example) that the initial population had an effect on genetic algorithm convergence. It was shown that some attention to the initial population may have had an effect on genetic algorithm success and further research and discussion was encouraged. Topics for future research included a different initial population for specific types of problem and it was observed that complex system planning required many linear programming problems to be resolved to obtain the objective function value so the final solution would require resolving hundreds or thousands of linear programming (LP) items (Gallego, 2003).

The theory behind the variable neighbourhood search (VNS) algorithm was developed in (Hansen, 2003).The VNS algorithm systematically exploits the idea of neighbourhood change, both in descent to local minima and escape from the valleys containing them(Hansen, 2003). It also makes the interesting remark that local optimal minima tend to be close to one another in many combinatorial and global optimisation problems and are situated in one (or sometimes several) small parts of the space search. So, once a local optimum has beenreached, it contains implicit information about close better, and perhaps globally optimum, ones. Therefore, a local optimum often provides some information about a global one. The case may be, for instance, that several optimal solutions have variables having the same value. In other words, researchers have found that optimal local solutions are related in many cases and concentrate on a quite limited part of the search space. In fact, if local optima were far apart and uniformly distributed in the search space, all metaheuristic techniques would be inefficient (Hansen,2003). Therefore, the ideal initial population for genetic algorithms should consist of local optima, each representing a different valley. With such initial population it becomes relatively easy to find a global optimal or sub-optimal solution.

This work involves these ideas by combining several traditional heuristics producing good quality local optima in short times and which are moderately robust. A set of good solutions was generated by making small alterations to a constructive algorithm. If this set were used as initial population, a genetic algorithm finds better solutions in highly-complex systems compared to a random initial population. The model consisted of the following DC model:

(1)

s.a.

(2)

(3)

(4)

Where represented, respectively, the cost of one circuit that can be added to right-of-way ij , that circuit´s susceptance, the number of circuits added in right-of-way i-j, the number of circuits in the base case, total power flow and the corresponding maximum power flow by circuit in right-of-way i-j . v was investment, S was the anchnode incidence matrix transpose, f was a vector having elements f_ij , g was a vector having elements g_k (generation in bus k) whose maximum value was was the maximum number of circuits which could be added to right-of-way i–j and Ωwas the set of all rights-of-way.

Constraint (2) modelled Kirchhoff´s current law (KCL) in the equivalent DC distribution network and constraint (3) modelled Kirchhoff´s voltage law (KVL). These constraints were non-linear constraints. The transmission expansion formulated above was an integer non- linear mixed problem (INLMP). It is a difficult combinatorial problem which can lead to the combinatorial explosion of the number of alternatives to be searched. However, continuous values are allowed for variable nij then the DC model becomes a non-linear problem (NLP).

The relaxed models used in transmission expansion planning are shown, as well as constructive heuristics used to generate initial populations. Test results and comparisons for the genetic algorithm in question are shown.

Relaxed models in expansion planning

The DC model is considered ideal for research in transmission planning. This model is used both in its complete version and its relaxed versions. It is relaxed if some of its constraints are eliminated and/or if the number of added elements is non-integer. In large-sized, very complex problems, a feature of met heuristics is that they do not explore complete solution space; instead, they make simultaneous explorations in many subspaces, frequently leading to low quality solutions. The relaxed versions of the DC model are crucial in optimising because they help to identify regions where promising solutions are located, giving excellent reference points for searching in met heuristics.

The relaxation of the DC model makes the solution space continuous which, when solved using LP in association with a constructive heuristic algorithm (CHA), leads to identifying regions containing very good quality solutions where the optimal solution can eventually be found.

There are several solution proposals for transmission expansion planning when some DC model constraints are relaxed. The two most important relaxed versions are the transportation model and the hyid model.

The transportation model

The transportation model (TM) was obtained by relaxing nonlinear constraints (3) in the DC model (Garver, 1970; Romero, 2002; Escobar, 2010). The model was simplified by eliminating non-linear characteristics implicit in planning. The new relaxed model was an integer linear mixed problem (ILMP) taking the following form:

(5)

s.a.

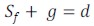(6)

(7)

An optimal solution for the TM can be found by using, for example, a anch and bound algorithm (Haffner, 2001; Gallego, 2007). However, this algorithm cannot find an optimal solution for a large-sized, complex planning problem. Obviously, if continuous values were allowed for variable nij,then the transport model would become a simple LP.

The hyid linear model

The hyid linear model (HLM) was obtained by relaxing nonlinear constraints (3) for the new circuits added to a system. It should be noted that type (3) constraints for already existing circuits in current topology were linear. Therefore, this model was an intermediate version between TM and DC models. The new relaxed model was an integer linear mixed problem (ILMP) taking the following form:

(8)

s.a.

(9)

(10)

(11)

(12)

Where S⁰ was the node-anch incidence matrix transpose of the system, made up of existent anches in initial topology and the buses connected to those anches, f0was the vector of power flows through the anches of the initial topology, with elements f ⁰_ij , S was the incidence matrix transpose of the complete system, and f was the vector of power flows of new circuits added to the system. Therefore, Ω was the group of indexes of existent circuits in base topology.

An optimal solution for HLM can be obtained by using, for example, a anch and bound algorithm as in the TM case. Again, this type of algorithms can not resolve large sized, great complexity optimisation problems. Also, in this case, if continuous values were allowed for variable n_ij then HLM would become an LP.

It should be observed that new circuits added to the system were not forced to satisfy KV Linan optimal solution for HLM. A new circuit added to the system could carry a different power flow than a circuit in parallel of the same type which was in the base topology (the existent one complies with both Kirchhoff´s laws but the new one only complies with the first). Ahyid non- linear model (HNLM) can be formulated in which all new circuits added to the system in parallel with existent circuits in base topology satisfy both Kirchhoff´s laws. However, this problem is an integer non-linear mixed problem (INLMP) having complexity close to that of the DC model. This type of model was not examined in this paper. Promising regions were identified in this paper by using CHA and relaxed models to generate excellent initial configurations for genetic algorithms.

Constructive heuristic algori thms in expansion planning

A constructive heuristic algorithm (CHA) is an iterative solution providing good solutions to complex problems. The CHA generally finds optimal solutions for small systems in applications like transmission expansion planning. However, as problem complexity increases, the solutions found are farther from being optimal. Different versions of the CHA that use relaxed versions of the DC model are presented next.

Garver´s algorithm

Garver was the first to propose a systematic CHA for planning (Garver, 1970; Escobar, 2010). Garver´s CHA finds good quality TM configurations. Obviously, the topology found by Garver´s CHA is not generally suitable for the DC model.

The basic structure of Garver´s CHA was used for proposing other CHAs for planning. The other CHAs that appeared after Garver´s original proposal differed from it in three aspects: they use a different model, different sensitivity indicator and local optimisation. The basic structure of a CHA for planning is presented here. It turned out to be a generalisation of Garver´s algorithm. A generalised CHA for planning took the following form:

1. Base topology was assumed as current topology and a mathematical model was chosen (TM, HLM, DC model, etc);

2. LP for the chosen mathematical model and for the current onfigurationwas solved. If LP solution indicated that the system operated without problems for current topology, then feasible topology for the chosen model had been found and was good quality for planning(in this case, step 4 would have been nextor, otherwise, step 3);

3. A sensitivity indicator was used to identify the most attractive circuit to be added to a system. Current topology was updatedby adding one or several of the identified circuits(step 2 would have been next); and

4. The added circuits were sorted in descending order by cost and an LP used in each case to verify whether the removal of a circuit would maintain the system in appropriate operating conditions. If the system operated adequately, then such circuit was removed. Removal simulation was repeated with all circuits.

Step 4 was necessary in CHA because some circuits added during solution were irrelevant in the final solution.

The remaining CHAS were obtained by starting generalised CHA. Therefore, Garver´s CHA was a generalised CHA having the following haracteristics: it used TM, the sensitivity indicator was the power flow through the added circuits provided in LP solution for TM and whose relaxation consisted of allowing continuous values for integer variables and it did not use the simulation strategy of removing the added circuits implemented in step 4.

Step 2 in Garver´s CHA solved the LP for TM considering only n_ij ≥0 and step 3 selected circuit n_ij ≠0 having the largest power flow. The power flow through the new circuits(not necessarily integer)was the sensitivity indicator for Garver´s CHA. Obviously, generalised CHA step 4 could be incorporated into Garver´s CHA and another sensitivity indicator could be used, such as the circuit having the largest nij value found in resolving LP in step 2.

Algorithms for the hyid linear model

Three CHAs could be implemented for HLM in planning by simply changing the logic for the behaviour of new circuits added to the system during each step. Three types of behaviour could be selected for each new circuit added to the system. All circuits added to a system only comply with Kirchhoff´s current law (KCL),new circuits added in parallel to other circuits of the same type in base topology should obey both Kirchhoff´s laws (KVL and KCL) but circuits added in new paths should only obey KCL and all circuits added should obey both KL. Each strategy led to different CHAs and different final configurations; in all cases, base topology circuits had to obey both KL. In the three cases, the sensitivity indicator could be that used in Garver´s CHA.

Hyid algorithm I

This algorithm type will be called constructive hyid heuristic algorithm I (CHHA-I). All circuits added had simply to obey KCL and circuits in base topology had to obey both KL. In spite of this, this algorithm added more circuits to the system than Garver´s CHA and the obtained configuration was usually unfeasible for the DC model.

The CHHA-I for HLM was a generalised CHA with the following characteristics: it used the hyid linear model (HLM) and Garver´s sensitivity indicator. The newest and most important circuit was thus that taking the largest power flow in resolving the LP. Therefore, current topology LP for the HLM model was solved in step 2considering only n_ij ≥ 0 and circuit n_ij ≠0 taking the largest power flow was chosen in step 3, i.e. .

An LP slightly different to the HLM presented in (8)-(12) was solved in step 2 above for implementing the CHHA-I. The relationship Sf + Sofo + g = d was thus substituted for relationship Sf + Sofo+ S'f' = d where S' was the node-anch incidence matrix obtained from added circuits and f' was the vector for power flows through the added circuits, with elements f'_ij . A new group of constraints had to be added. It should be noted that the new LP had three flow vectors:a flow vector for existent circuits in base topology, a flow vector for the added circuits and a third flow vector for the new circuits that had to be added to the solution of the LP, based on current topology.

Hyid algorithm II

In the constructive hyid heuristic algorithm II (CHHA-II), the added circuits which were parallel to existent circuits of the same type in base topology had to obey both KL and circuits added to new paths had only to obey the KCL. In principle, this algorithm should have added more circuits to the system than CHHA-I, although it was also generally unfeasible for the DC model.

This algorithm differed from the CHHA-I in the type of LP solved during step 2.

To implement the CHHA-II, a slightly different LP to the HLM presented in (8)-(12) had to be solved in step 2. The same modifications as for CHHA-I were thus applied, i.e. the relationship Sf + Sofo + g = d had to be substituted by the relationship Sf + Sofo+ S'f' = d , although in this case S' was the node-anch incidence matrix formed by the added circuits corresponding to paths in which no circuits were present in base topology and f′ was the vector for power flows through circuits added in new paths, with elements f'_ij. Also, a new group of constraints had to be added for all circuits added in new paths. In addition, whenever a circuit was added in a anch in which there was already at least one circuit in base topology, the n^o_ij vector had to be updated.

Hyid algorithm III

In constructive hyid heuristic algorithm III (CHHA-III), all added circuits satisfied both KLs. The fundamental aspect of this algorithm was that final topology was feasible for the DC model. This important property arose from the fact that all added circuits obeyed both KLs. The iterative process stopped when balance load-generation was satisfied. This algorithm was proposed by Villasana-Garver-Salon (VGS) (Villasana, 1985).

To implement the CHHA-III, a LP slightly different from the HLM presented in (8)-(12) had to be solved in step 2. Thus, continuous values for integer variables nij≥0 had to be allowed. Additionally, in each step of the algorithm, the vector n⁰_ij was updated with the addition of every new circuit and, whenever a circuit corresponding to a new anch was added to the system, set Ω had to be updated also.

Algorithms for the DC model

Many existing heuristic algorithms and CHAs work directly with the DC model and, therefore, find feasible and good quality topology for the DC model. Only the two CHA used in this paper are examined. CHAs have been widely applied in electricity transport planning in versions called least effort criterion (LEC) and least load loss (LLL).

In each CHA step, LP for current topology was solved from the information from base topology and the added circuits. The type of LP that each CHA solved had to be identified. It should be noted that if values for n_ij(added circuits) were known in the DC model (1)-(4), the resulting problem would be a system of equations and inequations whose solution may or may not have be en feasible. To help in the solution, the system of algeaic equations and inequations could be transformed into a new LP having new variables representing the so-called artificial generators, one for each load bus. Therefore, for current topology k, the resulting LP that the CHA solved would have assumed the following form:

(13)

s.a.

(14)

(15)

Where n^k_ij represented the circuits added to find the current topology k, Ω₀ was the group of indexes for the existent circuits in the current topology, r was the vector of artificial generators whose elements were r_s in each load bus, and Γ was the group of indexes for the load buses; w was a measure of the problem´s unfeasibility and w = 0 indicated that the system operated appropriately.

Least effort criterion algorithm

The least effort criterion algorithm (LEC) (Monticelli, 1982; Escobar, 2010) is a generalised CHA having the following characteristics: it uses the DC model, the sensitivity indicator identifies the most important circuit producing the largest distribution of flows once added to current topology, it uses a fictitious network to solve disconnected node problems and solves a slightly different LP from that described in (13).

The CHA of LEC allowed circuit overload in LP solution. Therefore, power limit constraints were eliminated for lines and transformers in the model. The solution of each LP finished with w=0 since the circuits could be overloaded. Circuit addition in the CHA of LEC stopped when there were no overloaded, real or fictitious circuits. The criterion used for selecting new circuits was:

Where θ values were obtained from solution of the LP and γij was the susceptance of a circuit in path (i, j). The most attractive circuit was that having the largest absolute value in IS_ij. The CHA of LEC uses a fictitious network having adequate susceptance values in a sufficient number of paths to have the whole system connected to make the solution of the system always finish with w = 0 and to have values of θ available (for calculating IS_ij). The fictitious network´s circuits were only used when there was no way to overload the normal circuits.

Least load loss algorithm

The least load loss algorithm (LLL) (Pereira, 1985; Escobar, 2010) is similar to the LEC algorithm and the only difference between them is that in the former the sensitivity indicator identifies the most important circuit that produces the largest decrease in load cut once added to current topology.

In the resolving LP, the CHA of LLL did not allow overload in the circuits and operational problems were represented by load shedding in current topology. If the solution of the LP finished with w ≠ 0 , then the system did not operate properly and more circuits had to be added to current topology. Adding circuits to the CHA of LLL stopped when the solution of the LP presented zero load shedding. The criterion used for selecting new circuits in the LLL algorithm was:

Where ^πj was the Lagrange multiplier of constraint j from the group of constraints (14). The most attractive circuit was that having the largest value in ISij. To be able to compute the values of IS_ij, the CHA of LLL required a fictitious network to have the complete system connected.

More than one circuit could be added in the two CHAs using the DC model, generating paths connecting isolated nodes with the rest of the system. The two CHAs could include normalisation by dividing the ISij by c_ij.

Using traditional heuristic algorithms in expansion planning

The importance of generated topologies for CHA

The topologies found using CHA can be used in several ways within metaheuristic structure. A topology found by a CHA can be considered good if it shows one or both of the following characteristics: it has a good objective function (i.e. it represents a quality investment proposal) and the topology has a high percentage of circuits forming part of optimal topology. These two characteristics do not always concur in any one topology regarding planning.

Topology having good objective function can be considered suboptimal. Such topology can be used in a GA´s initial population. Topology having a high number of circuits from optimal topology is fundamental in optimisation methods like GA because it can be transformed into optimal topology by means of appropriate operators. Virtually all topologies found by CHA have a significant number of circuits forming part of the optimal topology.

An initial GA population can be considered high quality if the circuits forming part of optimal topology are distributed in different initial population topologies (Goldberg, 1989).

In this case, the selection and recombination operators can collect all these circuits into a single topology, incorporating them in optimal or suboptimal configurations. If circuits from optimal topology are not present in the initial population, the only way to build optimal topology is by means of the mutation operator, which is considered a secondary operator in the GA.

Initial randomly-generated populations have a reduced number of circuits in optimal configuration for large-size systems in planning. Mutation should thus generate these circuits, increasing the GA´s computational effort. Relaxed models and CHAs were used in this paper in generating the initial population for the GA having characteristics regarding optimal or sub-optimal solutions requiring the addition of a large number of circuits, as in the] case of the Brazilian North-Northeastern test system.

Generating topologies for metaheuristics

The following procedure was used for generating a group of ifferent topologies for each mathematical model and each CHA analysed:

1. The best topology for the mathematical model selected and for the chosen CHA was generated. Supposing that circuits were added in p paths and that k ≤ p different topologies were to be found, p circuits were sorted in descending order regarding cost; and

2. The information for each of the first k circuits sorted in th previous step was used to find k new topologies. Each new topology was obtained by repeating step 1 but, in each case, adding one of the k circuits was forbidden. This process could be easily implemented, temporarily increasing the cost of the circuit analysed to avoid its selection.

The previous strategy generated k + 1 different topologies for the mathematical model and the selected CHA. Topology diversity could be increased through small changes in the iterative process, such as: modifying the sensitivity indicator if alternative proposals existed, eliminating step 4 from the generalised CHA and finishing the process before stopping criterion in generalised CHA was met and forbidding some of the k circuits found by the basic algorithm.

In the first case, the sensitivity indicator could be modified in Garver´s algorithm and the circuit having the largest value n_ij added and/or simultaneously the integer part of all the circuits after resolving the first LP had also been added. These modifications could also be implemented in all the CHAs for the hyid model. Such sensitivity indicator could be normalised in least effort criterion and least load loss algorithms by dividing the factores de sensibilidad de MCC y CME, éstos pueden ser modi original value by circuit cost. The second proposal is simpler and seeks to keep excess circuits added by the CHA and which maybe interesting for the DC model. The third modification seeks to avoid the irrelevant addition of circuits in final CHA phase. A large number of circuits are usually added during the final CHA phase to solve small demand problems in distant buses. Therefore, the process can be stopped prematurely to avoid adding irrelevant circuits. The last property was included to augment initial population variability. This strategy produced a large number of good initial topologies and was used to generate an initial population for the GA.

Applying the genetic algorithm

The topologies found by the CHA can be used in different ways within the structure of metaheuristics. In this paper these topologies were used to generate an initial population in a GA.

The genetic algorithm used was basically an improved version of the GA presented in (Gallego, 1998a). For more details on the theory of genetic algorithms and metaheuristics see (Glover, 2002), and for their application to planning see (Gallego, 1998a; Da Silva, 2000). An initial population was regarded as having excellent quality if optimal topology genes were distributed among the elements constituting it. The initial population generated using the CHA for the different models was applied to 4 electricity distribution systems: (1) the Garver system with 6 buses, 15 anches and 760 MW demand, (2) the Southern Brazilian system (SB) with 46 buses, 79 anches and 7,660 MW demand, (3) the Colombian system in 2012 with 93 buses, 155 anches and 14,559 MW demand and (4) the North-Northeast Brazilian system in Plan P1 with 87 buses, 183 anches and a demand of 20,316 MW. These 4 systems were selected because they present different levels of complexity. It should be noted that a large-sized system does not necessarily present great complexity. A system is regarded as being highly complex during planning if it presents a high level of disconnection and requires many additions to optimal topology. Only the first two systems had enough data to carry out planning both with and without rescheduling generation and had a well-known optimal solution. Only sub-optimal solutions were knownfor the other systems.

The optimal solution was identified for the Garver system by almost all CHA and it therefore formed the initial population. For the Southern Brazilian system (SB), all solution circuits were distributed in the initial population and, although no CHA identified the optimal solution, some CHAs identified solutions differing from the optimal only in one circuit. Anyway, having excellent quality initial configurations for resolving optimisation in the two previous systems, using metaheuristic methods only reduced computing time since, in low complexity systems like these, it is always possible to find the optimal solution even though the initial population has been randomly generated.

When applying the constructive heuristic algorithms described in this paper to the Colombian system in 2012, 14 of the 17 circuits from the best known solution were identified. An important characteristic of the CHA is that they frequently identify future network base structure while circuits from the best solution whose capacity is small are less frequently identified. The Colombian system was considered a large size and medium complexity system.

For the Brazilian North-Northeast system, 87.1% of the circuits from the best solution known were present in the initial population. In this system, it was difficult to quantify the amount of suboptimal circuits present in the initial population since there were many sub-optimal solutions having very similar investment values and radically different topologies. The concept of sub-optimal circuit depended on the sub-optimal topology taken as reference. A more interesting aspect was that the circuits present in the best solution forming the initial population represented 97.77% of investment in the best known solution. In other words, the circuits identified were the most important and the most expensive in the best known solution. Table 1 shows the comparative results for the different systems used.

The genetic algorithm should have found circuits which are not present in the initial population using the mutation operator. Obviously the selection and/or mutation operator can eliminate optimal circuits in the initial population and, in such cases, the mutation operator must reconstruct them. Also, a GA using good quality initial population must use low selective pressure (i.e. the survival of topologies having low quality objective function must be preserved).

Test and results

In this case, only the results obtained for the Colombian and the Brazilian North-Northeast systems are shown.

Colombian system

This system´stopology and data were available in (Escobar, 2002). The GA using an initial population generated in the way presented in this paper found the best solution known for the Colombian system. Thus, the best solution obtained, with an investment of v = 560 million dollars and load cut of w = 0.2 MW had the following topology:

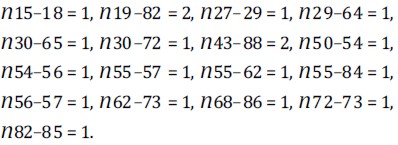
Also, the best solution obtained with w = 0 MW had v = 562,42 investment. Table 1 shows the quantity of anches identified by the CHAs corresponding to the best solutions. To find these configurations, the GA solved around 4,250 LP´s.

Brazilian North North-eastern system

The data for this system was available in (Escobar, 2002). Results for the P1 case are displayed. This was considered a high complexity system because it was highly disconnected and needed many transmission lines to find feasible solutions. Additionally, no optimal solution was known. Using the initial population generated for this paper, a solution having v = 1.356.712.000 US $ investment and w = 3.3 MW load cut was found. It had the following topology:

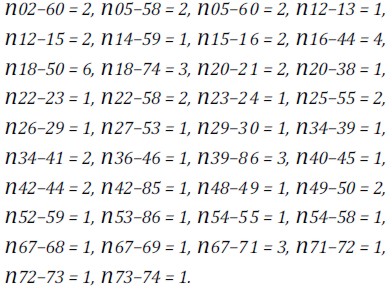
For w = 0 shedding load, the solution required an investment of v = 1.360.961.000 US $, and had following configuration:

Both solutions corresponded to the same region in the search space because they were topologically similar, having differences in only five paths. The GA solved around 80,000 LPs to find these configurations.

Results for the two solution strategies are shown for the Colombian system and Brazilian North-Northeast System. The same algorithm was used but different initial populations were used.

The algorithm was run ten times to compare their performance. Test were also run in which a premature cut was made, by contrast with runs where normal convergence was allowed. For the Colombian system, execution was stopped after 2,000 LPs and normal convergence was found after 20,000 LPs. For the Brazilian North-Northeast System, the cut was made after 20,000 LPs and convergence happened at 80,000 LPs. Table 2 shows the results, where LP indicates mean LP values for the ten runs and v indicates the best solution found.

Initial populations were generated in the following three ways: totally random (ALE), controlled random (ALC) and using constructive heuristic algorithms (CHA). A number of lines between 0 and the top limit were enerated for each path by the first strategy. For the second, np transmission lines were generated in a random np step process, where np was close to the number of lines in the best topologies for the system being studied. np = 20 values for the Colombian system and np = 65 for the Brazilian system were used. In Table 2, C means the Colombian system, C -ALE is the case using random, C-ALC controlled random and CCHA CHA generated initial population. Investment was measured in millions of US dollars. The results clearly showed superior performance for CHA regarding execution speed and solution quality. The difference was even greater in the Brazilian system because of its high complexity.

Conclusions

A genetic algorithm has been presented which was initialised with constructive heuristic algorithms and it has been shown that it was more efficient than the same algorithm using a random initial population; such difference could be highly significant in complex systems. The results coincided with observations made by other researchers investigating the effect of initialisation on genetic algorithms. The paper has also shown a new use for met heuristic techniques, namely as an auxiliary method for improving overall performance of the globally met heuristic optimisation technique. Based on this paper´s results and those in other publications, our results have indicated how a currently established initial solution can be restated (this would also apply to a set of initial solutions necessary for initialising any met heuristic algorithm). This might be very effective for engineering problems involving high mathematical complexity.

References

Da Silva, E.L., Gil, H.A., Areiza, J.M., Transmission Network Expansion Planning under an Improved Genetic Algorithm., IEEE Transactions on Power Systems, Vol. 15, No. 4, November, 2000, pp 1168-1175.

Escobar, A. H., Planeamiento Dinámico de la Expansión de Sistemas de Transmisión Usando Algoritmos Combinatoriales., Universidad Tecnológica de Pereira, tesis de Maestría, 2002.

Escobar, A. H., Gallego, R. A., Romero, R., Multistage and Coordinated Planning of the Expansion of Transmission Systems., IEEE Transactions on Power Systems vol. 9, no. 2, pp. 1565-1573, November 2004.

Escobar, A., Romero, R., Gallego, R. A., Modelos Usados en el Planeamiento de la expansión a Largo Plazo de Sistemas de Transmisión de Energía Eléctrica., Taller de publicaciones Universidad Tecnológica de Pereira, 2010, pp. 22-76.

Gallego, R.A., Monticelli, A., Romero, R., Transmission System Expansion Planning by Extended Genetic Algorithm., IEE Proceedings - Generation, Transmission and Distribution, Vol. 145(3), May, 1998a, pp.329-335

Gallego, R.A., Monticelli, A., Romero, R., Comparative Studies of Non-Convex Optimization Methods for Transmision Network Expansion Planning., IEEE Transactions on Power Systems, Vol. 13, No. 3, August, 1998b, pp.822-828.

Gallego, R.A., Monticelli, A., Romero, R., Tabu Search Algorithm for Network Synthesis., IEEE Transactions on Power Systems, Vol. 15, No. 2, May, 2000, pp. 490-495.

Gallego, R. A., Escobar, A., Romero, R., Optimización en Sistemas Eléctricos I - Programación Lineal., Taller de publicaciones Universidad Tecnológica de Pereira, 2003, pp. 77-218.

Gallego, R. A., Escobar, A., Romero, R., Programación Lineal Entera., Taller de publicaciones Universidad Tecnológica de Pereira, 2007, pp. 87-191.

Garver, L.L., Transmission Network Estimation Using Linear Programming., IEEE Trans. Power App. Syst., Vol. PAS-89, September-October, 1970, pp. 1688-1697.

Glover, F., Kochenberger, G.A., Handbook of Metaheuristics,Kluwer Academic Publishers., Boston/Dordrecht/LOndon, 2002, pp. 37-184.

Goldberg, D.E., Genetics Algorithms in Search, Optimization and Machine Learning, Addison Wesley, Reading, Massachusetts, 1989.

Haffner, S., Monticelli, A., Garcia, A., Romero, R., Specialized Branch and Bound Algorithm for Transmission Network Expansion Planning., IEE Proceedings -Generation, Transmission and Distribution, Vol. 148(5), September 2001, pp. 482 -488.

Hansen, P., Mladenovic, N., A Tutorial on Variable Neighborhood Search., Les Cathiers du GERAD, G-2003-46, July 2003.

Latorre, G., Cruz, R.D., Areiza, J.M., Villegas, A., Classification of Publications and Models on Transmission Expansion Planning., IEEE Transactions on Power Systems, Vol. 18, No. 2, May 2003, pp 938-946

Lee, C.W., Ng, S.K.K., Zhong, J., Wu, F.F., Transmission Expansion Planning From Past to Future., Power Systems Conference and Exposition, Oct. 29 2006-Nov. 1, PSCE ´06. IEEE PES, Atlanta, GA, USA, 2006, pp. 257 - 265

Maaranen, H., Miettinen, K., Penttinen, A., On Initial Populations of a Genetic Algorithm for Continuos Optimization Problems., Journal of Global Optimization, 37, 2007, pp 405- 436.

Monticelli, A., Santos, Jr. A., Pereira, M.V.F., Cunha, S.H., Parker, B.J., Praga, J.C.G., Interactive Transmission Network Planning Using a Least-Effort Criterion., IEEE Trans. Power App. Systems, Vol. PAS-101, No. 10, 0ctober, 1982, pp. 3919-3925.

Pereira, M.V.F., Pinto, L.M.V.G., Application of Sensitivity Analysis of Load Supplying Capability to Interactive Transmission Expansion Planning., IEEE Transaction on Power Apparatus and Systems, Vol. PAS-104, No. 2, Feuary, 1985, pp. 381 -389.

Romero, R., Monticelli, A., Garcia, A., Haffner, S., Test Systems and Mathematical Models for Transmission Network Expansion Planning., IEE Proceedings - Generation, Transmission and Distribution, Vol. 149(1), 2002, pp. 27-36.

Romero, R., Rider, M.J., Silva, I., A Metaheuristic to Solve the Transmission Expansion Planning., IEEE Transactions on Power Systems, Vol. 22, No. 4, November, 2007, pp. 2289- 2291.

Villasana, R., Garver, L.L., Salon, S.J., Transmission Network Planning Using Linear Programming., IEEE Trans. Power App. Systems, Vol. PAS-104, No. 2, Feuary 1985, pp. 349-356.