
A survey of repetitive control in varying frequency conditions
Germán Andrés Ramos Fuentes1, Josep Olm Miras2, Ramón Costa Castelló3
1 Master in Industrial Automation, Universidad Nacional de Colombia. Assistant Professor, Universidad Nacional de Colombia, Colombia. garamosf@unal.edu.co
2Ph.D. of Science (Physics), Universitat Politécnica de Catalunya. Dr. Assistant Professor, Universitat Politecnica de Catalunya, Spain. josep.olm@upc.edu
3 Ph.D. in Computer Science, Universitat Politecnica de Catalunya. Professor, Universitat Politecnica de Catalunya, Spain. ramon.costa@upc.edu
ABSTRACT
Digital repetitive control is a strategy that allows tracking/ rejecting periodic signals. Repetitive controllers are designed assuming that the exogenous signal period is constant and known, its main drawback being the dramatic loss of performance when signal frequency varies. This paper reviews the most relevant proposals advanced for overcoming this problem.
Keywords: repetitive control, varying frequency, high order repetitive control, varying sampling period.
Received: May 3th 2010
Accepted: July 1th 2011
Introduction
Repetitive control (RC) (Costa-Castelló et al., 2005; Tomizuka, 2008; Wang et al., 2009) is an internal model principle (IMP)- based technique (Francis and Wonham, 1976). The IMP establishes that in order to track/reject a certain signal the generator of such signal has to be included in the control loop. RC uses the IMP for tracking/rejecting periodic signals, assuming that these signals’ frequency remains constant and known. This yields the selection of a number of samples per period which are structurally incorporated into the control algorithm.
However, it has been shown that even slight changes in signal frequency yield dramatic performance decay (Steinbuch, 2002). This paper reviews the most relevant proposals for overcoming this problem.
Digital repetitive control
Digital implementation of RC implies external signal discretisation. Hence, a continuous Tp-periodic signal sampled with period Ts becomes a discrete N -periodic signal (N= Tp / Ts). The internal model of these types of signals came from Tomisuka (Tomisuka et al., 1989)4:
 | [1] |
Other types of internal models have been proposed depending on the specific type of signal to be dealt with (Escobar et al., 2007; Griñó and Costa-Castelló, 2005).
The main feature of (1) is that it has N poles uniformly distributed on the complex plane' s unit circle. Hence, the controller provides infinite gain at ω =2kπ/N frequencies, with k = 0, 1, 2, …,N-1. This high gain compromises system stability and robustness. Two additional filters are included to address this fact: Lz), used to assure stability and Q(z) aiming at providing robustness regarding unmodelled dynamics. Although ther are several structures, the most usual one is that shown in Figure 1. Here the RC is added to a controller, C(z) , specifically designed to stabilise the plant P(z). Therefore (1) becomes:
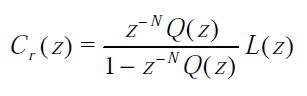 | [2] |

The RC structure was originally proposed in continuous time (Hara et al., 1988; Inoue et al., 1981) while the first digital implementation was reported in Nakano and Hara (1986).
Stability
Stability analysis of a closed-loop system (Figure 1) is important and this is why one follows the scheme proposed in Inoue (Inoue et al., 1981). The closed-loop system sensitivity function is:
 | [3] |
With So(z) = 1/(1+C(z)P(z)) and To(z) = C(z)P(z)/(1+C(z)P(z)) being, respectively, the system' s sensitivity function and complementary sensitivity function without RC, and SM(z) being the modifying sensitivity function, which shows the effect of the RC on s y s tem sensitivity:
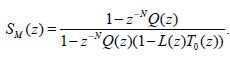 | [4] |
Hence, the system shown in Figure 1 would be stable if:
1. So(z) is stable, which arises from inner loop stability;
2. (1 z-NQ(z)) is stable, which may be fulfilled by defining Q(z) as a FIR filter;
3. ⁄Q(z)⁄< 1 ; and
4. ⁄1 To(z)L(z)⁄ <1
The design of L(z) is based on phase cancellation of To(z) (Inoue, 1990). For minimum phase systems, one takes L(z) = kΥ To-1(z), where 0 < kΥ < 2 ; and kΥ' are selected through trade-off between robustness and performance (Hillerström and Lee, 1997).
Applications
RC has been widely used in different areas, such as hard disk and CD drives (Chew and Tomizuka, 1990), robotics (Kasac et al., 2008; Sun et al., 2007), electro-hydraulic actuators (Kim and Tsao, 2000), vibration suppression (Daley et al., 2006; Hattori et al.,000), heat exchangers (álvarez et al., 2007), friction compensation (Huang et al., 1998), electrical injection molding machines (Nan et al., 2006), piezoelectric actuators (Choi et al., 2002), linear motor machine control (Chen and Hsieh, 2007), electronic rectifiers (Zhou and Wang, 2003), PWM inverters (Li et al., 2006; Wang et al., 2007b) and active filters (Costa-Castelló et al., 2009).
Performance
Performance in varying frequency conditions
Frequency is not exactly known or varies in most practical applications. Figure 2 shows internal model gain for signal period variations at harmonics k=1, 2 and 3. It can be noticed that performance decays dramatically the further away it is from the nominal period, and the situation becomes even worse for higher harmonics.

Performance faced with non-harmonic errors
Due to the waterbed effect (Songchon and Longman, 2001), RC controller sensitivity function shows amplification of frequencies between consecutive harmonics. This degrades system behavior and must be taken into account.
Organisation of the approaches
Several approaches have been proposed for resolving the performance issue when working with time-varying frequency signals. They can be grouped into two main sets: high order repetitive control (HORC) which uses several delay blocks to improve robustness and adaptive RC in which one or more controller parameters are adjusted on-line so as to maintain performance. The adjusted parameters are either sampling period (Ts) or the number of samples per period (N).
High order repetitive control
The internal model architecture used in HORC is shown in Figure 3, its transfer function being:

 | [5] |
where  , and usually
, and usually  . The modifying sensitivity function with HORC is:
. The modifying sensitivity function with HORC is:
 | [6] |
The stability conditions are coincident with already established ones, just replacing condition iii) by |W(z)Q(z) |< 1.
Weighting selection methods
Because of the excluding relationship between robustness regarding frequency variation and sensitivity to non-harmonic frequencies, selecting weighting wi is posed as an optimisation problem.
HORC is used in Inoue (Inoue, 1990) to improve harmonic frequency behaviour. The cost function to be minimised is the mean value of the square of SMW(z),  , which implies that all weighting must be equal and have a wi=1/m value.
, which implies that all weighting must be equal and have a wi=1/m value.
The goal in Chang (Chang et al., 1995) was to reduce the error spectrum, considering both harmonic and non-harmonic components,i.e.  .
.
Steinbuch (Steinbuch, 2002) aimed at reducing sensitivity to signal period variations. The first m derivatives of W(z) regarding signal period were zeroed. This allowed keeping a high gain for (5) in a wider neighbourhood around the harmonic frequencies. This problem exhibits an analytic solution.
Chang’s results (Chang et al., 1995) have been generalised in
Steinbuch (Steinbuch et al., 2007) through the solution of 
 being a weighting function establishing the interval in which the norm of SMW (ω) is to be minimised. Steinbuch (Steinbuch, 2002) and Chang' s (Chang et al., 1995) results corresponded to specific cases of this formulation.
being a weighting function establishing the interval in which the norm of SMW (ω) is to be minimised. Steinbuch (Steinbuch, 2002) and Chang' s (Chang et al., 1995) results corresponded to specific cases of this formulation.
Differently from the preceding approaches, the  constraint was removed in Pipeleers (Pipeleers et al., 2008). This reduces harmonic frequencies gains which leads to obtaining better performance results for non-harmonic frequencies. Steinbuch (Steinbuch, 2002; Steinbuch et al., 2007) and Chang’s (Chang et al., 1995) results corresponded to specific cases regarding this formulation.
constraint was removed in Pipeleers (Pipeleers et al., 2008). This reduces harmonic frequencies gains which leads to obtaining better performance results for non-harmonic frequencies. Steinbuch (Steinbuch, 2002; Steinbuch et al., 2007) and Chang’s (Chang et al., 1995) results corresponded to specific cases regarding this formulation.
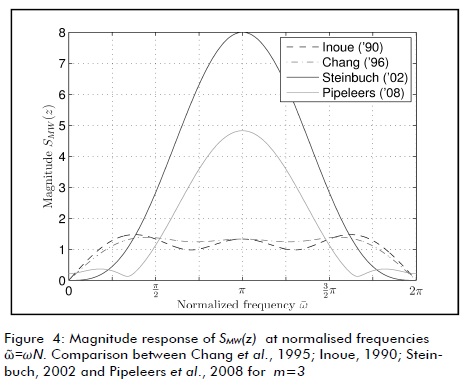
Figure 4 gives a comparison of the above proposals for m=3. Pipeleers' design (Pipeleers et al., 2008) for 20% uncertainty during the period had better results than Steinbuch (Steinbuch, 2002) for robust and non-harmonic performance. Notice that the gain at harmonic frequencies was not zero and it was lower for a wider frequency interval around the harmonics too. It may also be observed that, besides improving inter-harmonic behaviour, the approaches in Inoue (Inoue, 1990) and Chang (Chang et al., 1995) did not exhibit a robust design regarding period changes. The weights obtained with the aforementioned approaches are summarised in Table 1.

Adaptive repetitive control
Delay adaptation
The adjusted parameter is delay N in this strategy. There are two approaches: integer adaptation and fractional adaptation.
Integer delay. In varying frequency conditions (i.e. with variable Tp), the η = Tp/Ts ratio may take a non-integer value. Hence, the adaptation strategy consists of approximating N to the nearest integer to η, (Dotsch et al., 1995; Manayathara et al., 1996); a stability proof for systems with varying N is available in Hu (Hu, 1992).
Fractional delay. In this proposal, the integer part of η· keeps its original implementation 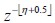 , while the fractional part is implemented using an FIR filter to approximate it (Laakso et al., 1996). FIR filter parameters are obtained through on-line optimisation using frequency error as a cost function (Wang et al., 2007a; Yu and Hu, 2001). Figure 5 plots a comparison of the results obtained with three different techniques.
, while the fractional part is implemented using an FIR filter to approximate it (Laakso et al., 1996). FIR filter parameters are obtained through on-line optimisation using frequency error as a cost function (Wang et al., 2007a; Yu and Hu, 2001). Figure 5 plots a comparison of the results obtained with three different techniques.

Varying sampling period
This section includes approaches where sampling period, Ts, is varied, aiming to keep the N=Tp/Ts,/ ratio constant.
An RC is applied to a peristaltic bomb in Hillerström (Hillerström, 1994) where disturbances are directly related to a mechanism' s angular position. Sampling period variations imply that system behaviour is not that of a linear time invariant (LTI) system; controller parameters therefore depend on sampling period.
This strategy’s effect on system stability is analysed in Ramos (Ramos et al., 2009) via a linear matrix inequality (LMI)-gridding approach (Apkarian and Adams, 1998; Sala, 2005).
Differently from the preceding one, Olm (Olm et al., 2011) presents a methodology for stability analysis based on robust control theory (Fujioka, 2008; Suh, 2008). Time varying components are treated as norm-bounded uncertainties. The obtained results yield conservatism reduction and wider stability intervals, compared to Ramos (Ramos et al., 2009).
A methodology for compensating for parametric changes due to sampling period variations has been presented by Olm (Olm et al., 2010). This is achieved by including a pre-compensator that cancels out the effect of the time-varying sampling and makes the closed-loop system invariant to sampling period changes.
Integer adaptation of delay with variable sampling period
N is obtained in Tsao (Tsao et al., 2000) via an integer approximation of the Tp/Ts ratio, as previously described, and Ts is readjusted so that external period Tp results in an integer multiple N of Ts . Although experimental results are provided, the study does not include a formal stability analysis.
Interpolators
Cao and Ledwich' s proposal (Cao and Ledwich, 2002) includes a system having two independent sampling periods; one is based on a loop with nominal sampling which is constant and includes the plant and a stabilising controller, while RC works with variable period using Tsao' s adaptation technique (Tsao et al., 2000). These parts are assembled with two interpolators which are located at RC control loop input and output. Each interpolator is in charge of reconstructing the signal from input samples and delivering it in the format of the corresponding output samples so that the two control actions can be added up. This structure is shown in Figure 6.

Spatial repetitive control
An RC for a rotatory system in which the disturbances directly depend on angular position is described in Chen and Yang (Chen and Yang, 2007). Instead of using non-uniform sampling (Hillerström, 1994), the proposal is to use spatial transformation resulting in a nonlinear position invariant (NPI) system. It is then linearised by feedback adaptation and a standard RC is introduced. The use of a nonlinear observer in Yang and Chen (Yang and Chen, 2008) means that the need for state measures can be removed.
Conclusions
This paper has described techniques proposed for tackling the problem of digital RC performance loss when working in variable frequency conditions. HORC leads to a higher computational burden and memory requirements, while sampling period variation involves higher technological complexity.
One has to estimate on-line signal frequency in adaptation schemes while the estimator is not actually needed in HORC schemes. HORC allows LTI analysis, while sampling period variation results in a linear time varying (LTV) framework which entails increased theoretical complexity for stability proofs.
Acknowledgements
This work has been partially supported by the Spanish ME (project DPI2010-15110).
Footnotes
4 This internal model was obtained from the Z-transform of discrete Fourier series expansion of periodic signal
References
álvarez, J.D., Yebra, L.J., Berenguel, M., Repetitive control of tubular heat exchangers. Journal of Process Control, Vol. 17, 2007, pp. 689-701.
Apkarian, P., Adams, R.J., Advanced gain-scheduling techniques for uncertain systems. IEEE Trans Control Syst Tech, Vol. 6, 1998, pp. 21-32.
Cao, Z., Ledwich, G.F., Adaptive Repetitive Control to Track Variable Periodic Signals With Fixed Sampling Rate. IEEE/ ASME Trans on Mechatronics, Vol. 7, 2002, pp. 374-384.
Costa-Castelló, R., Griñó, R., Cardoner, R., Fossas, E., High-Performance Control of a Single-Phase Shunt Active Filter. IEEE Trans on Control Systems Technology, Vol. 17, 2009, pp. 1318-1329.
Costa-Castelló, R., Nebot, J., Griñó, R., Demonstration of the Internal Model Principle by Digital Repetitive Control of an Educational Laboratory Plant. IEEE Trans Education, Vol. 48, 2005, pp. 73-80.
Chang, W.S., Suh, I.H., Kim, T.W., Analysis and Design of Two Types of Digital Repetitive Control Systems., Automatica, Vol. 31, 1995, pp. 741-746.
Chen, C.-L., Yang, Y.-H., Adaptive Repetitive Control for Uncertain Variable-Speed Rotational Motion Systems Subject to Spatially Periodic Disturbances., American Control Conference, 2007 ACC ' 07, 2007, pp. 564-569.
Chen, S.-L., Hsieh, T.-H., Repetitive control design and implementation for linear motor machine tool., Int Journal of Machine Tools and Manufacture, Vol. 47, 2007, pp. 1807- 1816.
Chew, K.K., Tomizuka, M., Digital control of repetitive errors in disk drive systems., IEEE Control Systems Magazine, Vol. 10, 1990, pp. 16-20.
Choi, G.S., Lim, Y.A., Choi, G.H., Tracking position control of piezoelectric actuators for periodic reference inputs., Mechatronics, Vol. 12, 2002, pp. 669-684.
Daley, S., Hätönen, J., Owens, D.H., Active vibration isolation in a mount using a repetitive control approach., Control Engineering Practice, Vol. 14, 2006, pp. 991-997.
Dotsch, H.G.M., Smakman, H.T., den Hof, P.M.J., Steinbuch, M., Adaptive repetitive control of a compact disc mechanism., Proc of IEEE Conf on Decision and Control, Vol. 2, 1995, pp. 1720-1725.
Escobar, G., Hernandez-Briones, P.G., Torres-Olguin, R.E., Valdez, A.A., A repetitive-based controller for the compensation of 6l\pm 1 harmonic components., Proc of the IEEE International Symposium on Industrial Electronics, 2007, pp. 3397- 3402.
Francis, B.A., Wonham, W.M., Internal Model Principle in Control Theory., Automatica, Vol. 12, 1976, pp. 457-465.
Fujioka, H., Stability analysis for a class of networked/embedded control systems: A discrete-time approach., American Control Conference, 2008, pp. 4997-5002.
Griñó, R., Costa-Castelló, R., Digital Repetitive Plug-in Controller for Odd-Harmonic Periodic References and Disturbances., Automatica, Vol. 41, 2005, pp. 153-157.
Hara, S., Yamamoto, Y., Omata, T., Nakano, M., Repetitive control system: a new type servo system for periodic exogenous signals., IEEE Trans on Automatic Control, Vol. 33, 1988, pp. 659-668.
Hattori, S., Ishida, M., Hori, T., Suppression control method for torque vibration of brushless DC motor utilizing repetitive control with Fourier transform., Proceedings of the 6th International Workshop on Advanced Motion Control, 2000, pp. 427-432.
Hillerström, G., On Repetitive Control., 1994.
Hillerström, G., Lee, R.C.H., Trade-offs in Repetitive Control., 1997.
Hu, J.-S., Variable Structure Digital Repetitive Controller., American Control Conference, 1992, pp. 2686-2690.
Huang, W., Cai, L., Tang, X., Adaptive repetitive output feedback control for friction and backlash compensation of a positioning table., Decision and Control, 1998 Proceedings of the 37th IEEE Conference on, 1998. pp. 1250-1251.
Inoue, T., Practical Repetitive Control System Design., Proceedings of the 29 IEEE Conference on Decision and Control, 1990, pp. 1673-1678.
Inoue, T., Nakano, M., Kubo, T., Matsumoto, S., Baba, H., High Accuracy Control of a Proton Synchroton Magnet Power Supply., Proc of the 8th IFAC World Congress, 1981, pp. 216-220.
Kasac, J., Novakovic, B., Majetic, D., Brezak, D., Passive Finite- Dimensional Repetitive Control of Robot Manipulators., IEEE Trans on Control Systems Technology, Vol. 16, 2008, pp. 570-576.
Kim, D.H., Tsao, T.-C., Robust Performance Control of Electrohydraulic Actuators for Electronic Cam Motion Generation., IEEE Trans On Control Systems Technology, Vol. 8, 2000, pp. 220-227.
Laakso, T.I., Valimaki, V., Karjalainen, M., Laine, U.K., Splitting the unit delay [FIR/all pass filters design]., Signal Processing Magazine, IEEE, Vol. 13, 1996, pp. 30-60.
Li, M., He, Z., Xing, Y., Analysis and Design of Repetitive controlled Inverter System with High Dynamic Performance., Power Electronics and Motion Control Conference, IPEMC 2006 CES/IEEE 5th International, 2006. pp. 1-5.
Manayathara, T.J., Tsao, T.-C., Bentsman, J., Rejection of unknown periodic load disturbances in continuous steelcasting process using learning repetitive control approach., IEEE Trans on Control Systems Technology, Vol. 4, 1996, pp. 259 -265.
Nakano, M., Hara, S., Microprocessor-based repetitive control. Microprocessor-Based Control Systems, 1986, pp. 279-296.
Nan, Y., Yu, L., Chen, Z., Wu, A., Study on Repetitive Controller for the Position Servo System of Electrical Injection Molding Machine., Intelligent Control and Automation, 2006 WCICA 2006 The Sixth World Congress on, 2006, pp. 8246-8250.
Olm, J.M., Ramos, G.A., Costa-Castello, R., Stability analysis of digital repetitive control systems under time-varying sampling period., Control Theory Applications, IET, Vol. 5, 2011, pp. 29-37.
Olm, J.M., Ramos, G.A., Costa-Castelló, R., Adaptive compensation strategy for the tracking/rejection of signals with timevarying frequency in digital repetitive control systems., Journal of Process Control, Vol. 20, 2010, pp. 551-558.
Pipeleers, G., Demeulenaere, B., Sewers, S., Robust High Order Repetitive Control: Optimal Performance Trade Offs., Automatica, Vol. 44, 2008, pp. 2628-2634.
Ramos, G.A., Olm, J.M., Costa-Castello, R., Digital repetitive control under time-varying sampling period: An LMI stability analysis., Control Applications, (CCA) Intelligent Control,(ISIC), IEEE, 2009, pp. 782-787.
Sala, A., Computer control under time-varying sampling period: An LMI gridding approach., Automatica, Vol. 41, 2005, pp. 2077-2082.
Songchon, T., Longman, R.W., On the waterbed effect in repetitive control using zero-phase filtering., Proc of the AAS/AIAA Space Flight Mechanics Meeting, 2001, pp. 1321-1340.
Steinbuch, M., Repetitive Control for Systems with Uncertain Period- Time., Automatica, Vol. 38, 2002, pp. 2103-2109.
Steinbuch, M., Weiland, S., Singh, T., Design of Noise and Period-Time Robust High Order Repetitive Control, with application to optical storage. Automatica, Vol. 43, 2007, pp. 2086-2095.
Suh, Y.S., Stability and stabilization of nonuniform sampling systems. Automatica, Vol. 44, 2008, pp. 3222-3226.
Sun, M.-X., He, X.-X., Chen, B.-Y., Repetitive Learning Control for Time-varying Robotic Systems: A Hybrid Learning Scheme., Acta Automatica Sinica, Vol. 33, 2007, pp. 1189-1195.
Tomisuka, M., Tsao, T.-C., Chew, K.-k., Analysis and Synthesis of Discrete-Time Repetitive Controllers., Journal of Dynamic Systems, Measurement and Control, Vol. 111, 1989, pp. 353-358.
Tomizuka, M., Dealing with periodic disturbances in controls of mechanical systems., Annual Reviews in Control, Vol. 32, 2008, pp. 193-199.
Tsao, T.-C., Qian, Y.-X., Nemani, M., Repetitive Control for Asymptotic Tracking of Periodic Signals With an Unknown Period., Journal of Dynamic Systems, Measurement, and Control, Vol. 122, 2000, pp. 364-369.
Wang, Y., Gao, F., III, F.J.D., Survey on iterative learning control, repetitive control, and run-to-run control., Journal of Process Control, Vol. 19, 2009, pp. 1589-1600.
Wang, Y., Wang, D., Zhang, B., Zhou, K., Fractional Delay Based Repetitive Control with Application to PWM DC/AC Converters., Control Applications, 2007 CCA 2007 IEEE International Conference on, 2007a, pp. 928-933.
Wang, Y., Wang, D., Zhou, K., Zhang, B., Ye, Y., Modelling and Robust Repetitive Control of PWM DC/AC Converters., IEEE Int Sym on Intelligent Control, 2007b, pp. 214-219.
Yang, Y.-H., Chen, C.-L., Spatially periodic disturbance rejection using spatial-based output feedback adaptive backstepping repetitive control., American Control Conference, 2008, pp. 4117-4122.
Yu, S.-H., Hu, J.-S., Asymptotic Rejection of Periodic Disturbances With Fixed or Varying Period., Journal of Dynamic Systems, Measurement, and Control, Vol. 123, 2001, pp. 324-329.
Zhou, K., Wang, D., Digital Repetitive Controlled Three-Phase PWM Rectifier., IEEE Transactions On Power Electronics, Vol. 18, 2003, pp. 309-316.