A thermodynamic evaluation of chilled water central air conditioning systems using artificial intelligence tools
Juan Carlos Armas1, Margarita Lapido Rodríguez2, Julio Rafael Gómez3, Yarelis Valdivia Nodal4
1 Mechanical Engineer, Doctor of Technical Sciences , Universidad de Cienfuegos, Cuba. jcarlos@ucf.edu.cu
2 Thermal Energy Engineer, Doctor of Technical Sciences, Universidad de Cienfuegos, Cuba. mlapido@ucf.edu.cu
3 Electrical Engineer, Doctor of Technical Sciences, Universidad de Cienfuegos, Cuba. jgomez@ucf.edu.cu
4 Mechanical Engineer, Master of Science, Universidad de Cienfuegos, Cuba. yvaldivia@ucf.edu.cu
ABSTRACT
An analysis of a chilled water central air conditioning system is presented. The object was to calculate main cycle component irreversibility, as well as evaluating this indicator' s sensitivity to operational variations.
Artificial neural networks (ANN), genetic algorithms (GA) and Matlab tools were used to calculate refrigerant thermodynamic properties during each cycle stage. These tools interacted with equations describing the system' s thermodynamic behaviour. Refrigerant temperature, when released from the compressor, was determined by a hybrid model combining the neural model with a simple genetic algorithm used as optimisation tool; the cycle' s components which were most sensitive to changes in working conditions were identified. It was concluded that the compressor, evaporator and expansion mechanism (in that order) represented significant energy losses reaching 85.62% of total system irreversibility. A very useful tool was thus developed for evaluating these systems.
Keywords: irreversibility analysis, energy, artificial neuronal network, genetic algorithm.
Received: February 12th 2010
Accepted: May 27th 2011
Introduction
Thermodynamic analysis of energy facilities has two objectives: determining a process' thermodynamic efficiency and finding the best strategy for such energy' s optimal use. Two approaches to systems analysis have thus been used to date: the so-called energetic approach based exclusively on the first law of thermodynamics and the exergetic approach supporting the energetic approach by including the second law of thermodynamics as a crucial part of current energy use. Analysis of the application of the first law cannot be separated from analysis of the second law, especially in systems involving associated work with or exploitation of energy sources at different temperatures. Applying both criteria constitutes a powerful tool for quantitative and qualitative evaluation of energy systems and processes thus enabling potential useful energy to be detected and assessing ways of optimising their use.
This study was aimed at evaluating refrigeration cycle behaviour by vapour compression in a chilled water central air conditioning system by adopting a thermodynamic approach. Irreversibility was determined for the cycle' s main components as well as their influence on the cycle' s total irreversibility. Their variability and impact on operational conditions was assessed. The use of artificial neural networks (for modelling and determining the refrigerant' s thermodynamic properties) and a genetic algorithm (describing the system' s behaviour) were incorporated as innovative tools for making the calculations. These artificial intelligence techniques facilitate calculation and simplify models. They have proved to be as accurate as more complex and rigorous thermodynamic models. In the particular case of this study, it was found that using these artificial intelligence tools outweighed the difficulties of thermodynamic modelling of some elements of the system being analysed with no loss or demerit regarding rigorous thermodynamics, for they are only used in relation to aspects like working substance reproduction properties.
The energy method and its application to refrigeration and air conditioning systems
Exergy analysis methodology is well established, mainly in the case of thermal power plants (Boer, 2005; Kelly, 2009; Lapido, 2006; Tsatsaronis, 2002; Valero, 2005). However, its application to refrigeration systems has not been equally extensive due to difficulties in understanding the implications of the concept of energy in these cycles, given that it is not ultimately aimed at producing useful work but to heat absorption in a particular room being conditioned.
Authors like Kotas (1985), Szargut (2004), Yumrutas (2002) d’Accadia (2004), Morosuk (2009) y Syed M. Zubair (2000) have approached this problem from different perspectives and with different purposes in mind. Szargut has stated that main energy losses in air conditioning systems are caused by compression inefficiency, heat rejected to the drain, pressure drop in ducts and heat loss in the expansion valve.
However, few reports have dealt with energy destruction in the cycle’s individual components caused by changes in operating conditions, an issue having significant importance in conditioning systems continuously subject to changing weather and occupation of the conditioned building.
Another difficulty in applying the exergetic method to refrigeration cycles lies in the definition of the reference temperature.
Some authors consider different reference states for primary and secondary refrigerant, for example, environmental temperature for the primary and water inlet temperature in the evaporator for the secondary refrigerant.
The duality of reference states for energy calculations is caused by air conditioning systems capability to work interchangeably with temperatures lower and higher than the environment. Negative energy thus flows at some points because of such system peculiarities, apparently contradicting the principles of thermodynamics. Szargut has solved this problem by adding the highest negative energy obtained to each energy flow in the system, thus changing the scale by lowering the reference system and turning all energy flows into negative energy flows in positive terms, a procedure used in this study.
Architecture of the artificial neural network used to obtain the properties of refrigerant R22
A neural network model for a multilayer network spreading forward with back propagation learning algorithm (Z.H.Z, 2005; Armas, 2006) was designed for obtaining R22' s pertinent thermodynamic properties. Artificial neural networks (ANN) for saturation areas, overheating and undercooling were designed and obtained. ANN were trained from the thermodynamic properties of R22, according to the literature (ASHRAE, 2009). The number of neurons in the hidden layer was obtained by trial and error for designing each neural network, starting from a small number of neurons. Options like validation and set tests with different training data were used to avoid overtraining.
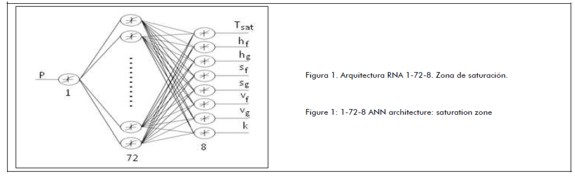
A saturation ANN was designed, having some special features distinguishing it from the others (Figure 1). It was structured with one neuron in the first layer for pressure (P), input variable, 72 neurons in the intermediate layer and 8 neurons in the third layer for output variables [saturation temperature (TSAT), liquid enthalpy (hf), vapour enthalpy (Hg), fluid entropy (sf), vapour entropy (sg), liquid specific volume (vf), gas specific volume (vg) and adiabatic coefficient (k)]. Tansig and purelin were used as transference functions in the first and second network output layers.

Figure 2 shows undercooling zone ANN. It consisted of three layers having two neurons in the first layer for input P and GSE (undercooling degrees). There were 100 neurons in the second layer and three for output in the last one [enthalpy (h), entropy (s) and specific volume (v)]. Transfer functions used for undercooling and overheating were similar to those for the saturation zone.

A four-layer network having 2 neurons in the first layer [input variables (P, Tsob)], 9 and 6 neurons in the intermediate layers and 3 neurons in the output layer was designed for the overheating zone.
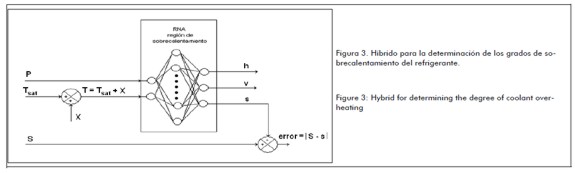
Hybrid model for determining compressor cooling system temperature for vapour compression
The refrigerant’s temperature when leaving the compressor was determined from a hybrid model combining the neural model with a simple genetic algorithm used as optimisation tool. The fitness function of this algorithm was an error function between gas entropy at evaporator outlet point (considering overheating degrees) and the entropy obtained from the refrigerant overheating area neural model. Zero error was achieved for this neural model, ensuring that the results were obtained for an isentropic process.
Figure 3 gives a representation of the process followed in the genetic algorithm. Genetic variables were overheating degrees (X) and the search for this variable' s values guaranteed error minimisation.
Description of the installation base
A conventional refrigeration cycle through vapour compression in a chilled water central air conditioning system is presented in Figure 4; such system has two working circuits. The primary circuit uses a refrigerant, typically R-22 as considered in this work, but it could also have been R-123, R-134a or R-407 according to capacity and technology used in compression, the latter being more environmentally-friendly then the first. The secondary circuit distributed cold water to the rooms to be cooled.
Two different working systems were analysed:
1) Operational conditions involving primary circuit (with R-22) 482.48 kPa (-1°C) and 1,752.44 kPa (45°C) pressure, evaporation and condensation temperatures (in that order); 8.5°C and 10°C chilled water temperature in the initial impulse and the return were considered for the secondary circuit; and
2) Partial load scheme characterised by 460.91 kPa (-2°C) and 1,799.52 kPa (48.2°C) for pressure, evaporation and condensation temperatures, ensuring that water temperature remained unchanged.
Taking the work schemes for nominal conditions and partial installation which have been previously described as a starting point, the Matlab function detailed in section 1.6 was used.
Developing a Matlab function for evaluating the system
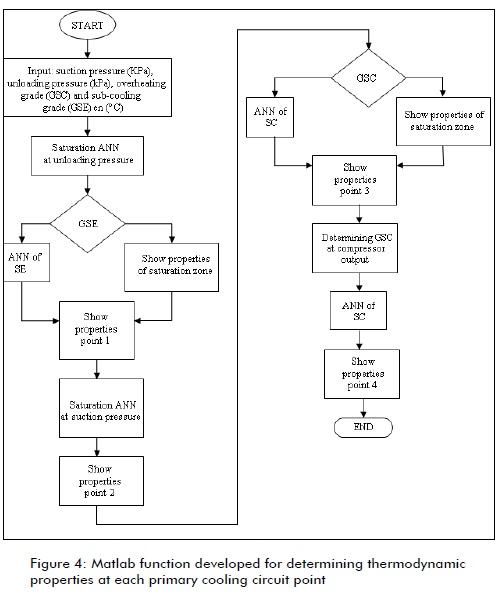
A function was created in Matlab to minimise computation time integrating the networks for each of the system' s working areas. The following aspects were defined as input variables: suction and discharge pressures and degrees of overheating and undercooling (if present in the cycle).
The function thus provided the refrigerant' s properties at each point of the primary refrigeration circuit. Figure 4 shows the algorithm for calculating refrigerant properties at different primary circuit points.
Integrating this function to a sub-programme including equations for the system' s thermodynamic behaviour led to creating an analysis set for air conditioning systems with no need for using specialised software which was difficult to adapt to the specifications required by the evaluators.
Thermodynamic analysis of the whole central heating system’s water
Some aspects were considered when making a thermodynamic analysis of the system. They were related to reference state temperature in both primary (R-22, 25°C) and secondary refrigerant (cold water, 10°C). Gas compression was considered to be adiabatic and the system' s energy flows were modified by adding the highest negative energy power values, thus changing the scale by reducing the reference system. All this was aimed at turning negative energy into positive ones without contradicting the laws of thermodynamics.
The function also led to calculating R-22 properties at each point of the cycle. The results provided in Table 1. were obtained from combining the sub-programmes with equations describing the system' s thermodynamic behaviour.

Table 1 shows that modifying working conditions in the installation (from nominal to partial scheme) resulted in decreased efficiency in both energy and energy studies, in turn, resulting in increased energy consumption. This can be corroborated by analysing compressor work when nominal installation conditions were modified; in fact, it increased by around 5%.
Irreversibility component analysis
Using Matlab functions led to determining local irreversibility for each component to evaluate energy destruction and to quantify each component' s impact on total system irreversibility. Table 2 provides a comparison between working schemes which have been studied to date to locate components that were more influenced by changes in the installation.

Table 2 shows that the compressor is the most irreversible element in a refrigeration system through vapour compression since it is provided with quality energy (pure energy) that is transferred to the coolant and then part of it is transferred during condensation, performing no useful work. The evaporator and expansion mechanism, in that order, are next in the list presenting significant energy losses. These three elements represent 85.62% of all total system irreversibility. An interesting feature highlighted in this study was capacitor function as process organiser (less irreversible) to conduct the working fluid to favourable conditions and eventually achieve the final installation effect.
It was observed when analysing Table 2 regarding each component' s energy variation that the most sensitive components were the condenser and expansion mechanism as a system' s operating conditions varied (Figure 5.).

Given these components' great sensitivity to the previously described type of variations, it became very important to control air conditioning system working conditions and modify parameters negatively affecting its efficiency.
As part of the cooling circuit, the capacitor is a very sensitive element, mostly to pressure changes; its functioning and pertinent pressure changes therefore depend on environmental temperature. One change that could be introduced would be controlling the speed of the machinery pumping the condenser’s cooling fluid (fans or pumps when it comes to air or water cooling, in that order). Condensation pressure would be considered as control variable.
The expansion mechanism constitutes a particular case. There must be an abrupt change in cross-section for the system to operate, leading the working substance from high energy potential to lower quality energy potential having no useful work. An unprofitable energy loss thus occurs (from a technological point of view). There is no way of reducing this loss.
Conclusions
1. The analysis of energy destruction for each refrigeration cycle component through vapour compression indicated that the most irreversible elements were the compressor and the evaporator. Both elements accounted for around 60% of total system irreversibility; they should therefore be monitored for any variation in the installation;
2. The analysis of installation sensitivity to changes in working conditions showed how sensitive changing working parameters may be regarding energy consumption. In this specific case, the change in the system' s operating pressure resulted in an increase in the compressor' s work (around 5%), thereby increasing power consumption and decreasing the cycle' s operation coefficient by around 4%;
3. Creating the function developed in Matlab led to a very useful, flexible tool to be adapted to other studies evaluating air conditioning systems. It also constitutes the first stage of subsequent thermo-economic optimisation of central air conditioning systems;
4. Artificial intelligence tools provide the potential for determining properties and high accuracy thermal system simulation. ANN and AG models have thus been integrated into developing physical models of components and thermodynamic modelling of systems. This procedure would be more complex if developed with other conventional methods; and
5. Air conditioning systems' high energy consumption proves that there is a need for research from the perspective of conceptually designing a system' s exergoeconomic costs and general impact on the environment that these types of system represent.
References
Armas Teyra, M. A., Gómez Sarduy, J. R., Mariño Stand, L. Sepúlveda Chaverra, J., Inteligencia Artificial Aplicada al Análisis de Sistemas Energéticos con Matlab., 2006, pp. 68-99.
ASHRAE Handbook Fundamentals., Thermophysical Properties of Refrigerants., 2009, pp. 30.1- 30.75.
Boer, D., Exergy and structural analysis of an absorption cooling cycle and the effect of efficiency parameters., Int. J. of Thermodinamics, ISSN 1301- 9724, Vol. 8, No. 4, 2005, pp. 191- 198.
D’Accadia, M.D., Vanoli, L., Thermoeconomic optimization of the condenser in a vapour compression heat pump International., Journal of Refrigeration, 27, 2004, pp. 433- 441.
Kelly, S., Tsatsaronis, G., Morosuk. T., Advanced exergetic analysis: Approaches for splitting the energy destruction into endogenous and exogenous parts., Elsevier Ltd., Energy 34, 2009, pp. 384- 391.
Kotas, T.L., The energy method of Thermal Power Plants Analysis., ed. Ed. Anchon Brendon, Londres,1985.
Lapido, M. J., Termodinámica Avanzada., Centro de Estudios de Energía y Medio Ambiente, Ed. Universidad de Cienfuegos, Cuba, 2006, pp. 4-81.
Morosuk. T., Tsatsaronis, G., Advanced exergetic evaluation of refrigeration machines using different working fluids., Energy, Elsevier Ltd., 2009, pp. 1- 11.
Sepúlveda Chaverra, J., Inteligencia Artificial Aplicada al Análisis de Sistemas Energéticos con Matlab., 2006, pp. 68-99.
Szargut, J.T., Optimization of the design parameters aiming at the minimization of the depletion non-renewable resources.,Energy, 2004.
Tsatsaronis, G., Park, M.H., On avoidable and unavoidable energy destructions and investment costs in thermal systems., Energy Convers Manage, 43, 2002, pp. 1259-70.
Valero, A., Lerch, F., Serra L., Royo, J., Structural theory and thermoeconomic diagnosis, Part II: Application to an actual power plant., Energy convension and management, 43, 2002, pp. 1503- 1518.
Yumrutas, R.M., Kunduz, M., Kano, M., Exergy analysis of vapor compression refrigeration systems., Exergy, an International Journal 2, 2002, pp. 266-272.
Xia, Z.-H. Z., Y., The application of artificial neural network in HVAC system., Machine Learning and Cybernetics, Vol. 8, 2005, pp. 4800-4804.
Zubair, S.M., Thermodynamic optimization of finite time vapor compression refrigeration systems., Energy conversion and management, 2000.