
DOI: https://doi.org/10.15446/innovar.v25n56.48991
Medidas dinámicas de predictibilidad en el índice S&P 500 y sus determinantes1
Dynamic Measures of the Predictability of the S&P 500 Index and its Determinants
Mesures dynamiques de prédictibilité dans l'indice S&P 500 et ses déterminants
Medidas dinâmicas de previsibilidade no índice S&p 500 e seus determinantes
Javier Humberto Ospina HolguínI
I Magíster en Ciencias de la organización y en Ciencias en economía Universidad del valle
Cali, Colombia
Grupo de investigación de solvencia y Riesgo Financiero
Correo electrónico: javier.ospina@correounivalle.edu.co
Correspondencia: Javier Humberto ospina Holguín. Departamento de Contabilidad y Finanzas. Facultad de Ciencias de la Administración. Universidad del Valle. Sede san Fernando. Calle 4B No 36-00. Edifício 124 - oficina 2035. Cali, Colombia.
Citación: ospina Holguín, J. H. (2015). Medidas dinámicas de predictibilidad en el índice S&P 500 y sus determinantes. Innovar, 25(56), 69-82. doi: 10.15446/innovar.v25n56.48991. ENLACE DOI: https://doi.org/10.15446/innovar.v25n56.48991.
Clasificación JEL: G17, C53, C58.
Recibido: enero 2013, Aprobado: Mayo 2014.
Resumen:
El objeto de este estudio es medir la predictibilidad del índice accionario estadounidense S&P 500 y establecer posibles determinantes de esta predictibilidad. La predictibilidad se ha estudiado ampliamente, pero en pocos casos mediante medidas dinámicas y per se, como se hace aquí. Para establecer la predictibilidad se utilizan la medida eta del campo de las redes neuronales, el valor p del test de la razón de varianzas del campo de la econometría financiera y el análisis de fluctuación sin tendencia del campo de la econofísica. Se construye un algoritmo de inversión basado en las medidas dinámicas de predictibilidad que es mejor que la estrategia de comprar y mantenerse en el periodo estudiado. Para la medida más promisoria, se establece una relación empírica entre la predictibilidad y varios factores económicos y financieros. El panorama que arroja este estudio es el de un mercado que no es estáticamente predecible, sino cuya predictibilidad evoluciona dinámicamente en el tiempo, lo cual es compatible con la hipótesis del mercado adaptativo.
Palabras Clave: Predictibilidad, medida eta, test de la razón de varianzas, análisis de fluctuación sin tendencia, hipótesis del mercado adaptativo.
Abstract:
The purpose of this study is to measure the predictability of the S&P 500 US stock index and identify its possible determinants. Though predictability has been broadly studied, in very few cases it has been approached via dynamic measures, as done in this work. In order to establish predictability we used the eta measure of the field of neural networks, along with the p-value of the variance ratio test of financial econometrics, and detrended fluctuation analysis from the field of econophysics. We built an investment algorithm based on dynamic measures of predictability which results better than the strategy of buying and holding in the period studied. For the most promising measure, an empirical relationship between predictability and various economic and financial factors is established. This study points at the picture of a market that is not statically predictable, but whose predictability dynamically evolves over time in accordance with the adaptive market hypothesis.
Key words: Predictability, eta measure, variance ratio test, detrended fluctuation analysis, adaptive market hypothesis.
Résumé:
L'objet de cette etude est de mesurer la prédictibilité de i'indice boursier américain S&P 500 et d'etablir de possibles determinants de cette prédictibilité. La prédictibilité a fait l'objet de nombreuses études, mais rarement à travers des mesures dynamiques et per se, comme c'est le cas ici. Pour établir la prédictibilité on utilise ici la mesure êta des réseaux de neurones, la valeur p du test de la raison de variances du champ de l'éco-nométrie financière, et l'analyse de fluctuation sans tendance du domaine de l'éconophysique. On construit un algorithme d'investissement basé sur les mesures dynamiques de prédictibilité qui est meilleur que la stratégie d'acheter et se maintenir sur la période étudiée. Pour la mesure la plus pro-metteuse on établit une relation empirique entre la prédictibilité et divers facteurs économiques et financiers. Le panorama que dresse cette étude est celui d'un marché qui n'est pas statiquement prédictible, mais dont la prédictibilité évolue de façon dynamique dans le temps, ce qui est compatible avec l'hypothèse des marchés adaptatifs.
Mots-clés: Prédictibilité, mesure êta, test de la raison de variances, analyse de fluctuation sans tendance, hypothèse des marchés adaptatifs.
Resumo:
O objeto deste estudo é medir a previsibilidade do índice acio-nário americano S&P 500 e estabelecer possíveis determinantes dessa previsibilidade. A previsibilidade foi estudada amplamente, mas em poucos casos através de medidas dinâmicas e por si só, como se faz aqui. Para estabelecer a previsibilidade, utilizam-se a medida eta do campo das redes neuronais, o valor p do teste da razão de variâncias do campo da econometria financeira e a análise de flutuação sem tendência do campo da econofísica. Constrói-se um algoritmo de investimento baseado nas medidas dinâmicas de previsibilidade que é melhor que a estratégia de comprar e manter-se no período estudado. Para a medida mais promissora, estabelece-se uma relação empírica entre a previsibilidade e vários fatores econômicos e financeiros. O panorama que este estudo apresenta é o de um mercado que não é estaticamente previsível, mas cuja previsibilidade evoluciona dinamicamente no tempo, o qual é compatível com a hipótese do mercado adaptativo.
Palavras-chave: Previsibilidade, medida eta, teste da razão de variâncias, análise de flutuação sem tendência, hipótese do mercado adaptativo.
Introducción
En este artículo se estudia la predictibilidad del índice accionario estadounidense S&P 500 mediante medidas de predictibilidad per se y de manera dinámica. Por "per se" se entiende que el énfasis del presente artículo es el de utilizar medidas de predictibilidad que detecten los patrones en la serie misma de los retornos en lugar de utilizar medidas que detecten qué tan bien predicen un valor futuro otras variables externas rezagadas en el tiempo. Por "dinámica" se entiende que utilizamos estas medidas de predictibilidad sobre una ventana de los datos que se desliza en el tiempo para capturar la variabilidad temporal de la predictibilidad. Las tres medidas de predictibilidad utilizadas son: la medida eta del campo de las redes neuronales, el valor p del test de la razón de varianzas del campo de la econometría financiera y un exponente basado en el análisis de fluctuación sin tendencia del campo de la econofísica. Con base en cada medida de predictibilidad, se construyó un algoritmo de inversión que considera entrar al mercado solo cuando este es más predecible según la medida. Los tres algoritmos desarrollados superaron a la estrategia de comprar y mantenerse. Posteriormente se estudió para la medida con mayor rentabilidad la relación empírica entre esta predictibilidad y varios factores económicos y financieros, y se confirmó que existe una relación. Como factores relevantes se utilizaron los factores de un análisis factorial a partir de medidas que comúnmente se asocian al valor en la economía. El panorama que arroja este estudio es el de un mercado que no es estáticamente predecible, sino cuya predictibilidad evoluciona dinámicamente en el tiempo, lo cual es compatible con la hipótesis del mercado adaptativo (Lo, 2004).
El estudio de la predictibilidad del mercado de valores tiene implicaciones teóricas importantes, así como en la práctica: teóricamente, es interesante vincular la predictibilidad a otros factores económicos y financieros; empíricamente, la búsqueda de una mayor predictibilidad conforma la ocupación normal de los que comercian con acciones, especialmente las entidades institucionales.
La literatura sobre la predictibilidad de los retornos del mercado de valores es muy amplia, con trabajos tempranos como los de Fama y schwert (1977), Keim y stambaugh (1986) , French, schwert y stambaugh (1987), Campbell (1987) , Campbell y shiller (1988a, 1988b), Fama y French (1988a, 1988b), y especialmente Fama y French (1989, p. 23) quienes concluyeron que "los retornos esperados son menores cuando las condiciones económicas son fuertes y son más altos cuando las condiciones son débiles". Trabajos posteriores que siguieron a estos intentos iniciales de establecer predictibilidad son los de Ferson (1989), Breen, Glosten y Jagannathan (1989), Harvey (1989), schwert (1989) y Jegadeesh (1990), quien estudió la predictibilidad a través de la correlación serial. En 1991, Cochrane establece, como un ejemplo del estado del arte en ese tiempo, que la prima de interés, la prima por quiebra, los rendimientos rezagados, la razón dividendo-precio y la inversión, entre otros, predicen los rendimientos de las acciones.
Durante la década de 1990, nuevos estudios corroboraron la predictibilidad de los retornos, incluyendo los de Ferson y Harvey (1991), Hodrick (1992), Bekaert y Hodrick (1992), Lamont (1998), Lewellen (1999), Nelson (1999) o Pontiff y schall (1998), quienes encuentran que las razones de libro a mercado contienen información sobre los retornos accionarios futuros que no está capturada por las brechas del rendimiento del interés ni por los rendimientos de dividendos. Por otra parte, algunos investigadores durante ese periodo empezaron a poner en duda la predictibilidad, incluyendo a Goetzmann y Jorion (1993), Bossaerts y Hillion (1999) y parcialmente a Pesaran y Timmermann (1995), quienes encontraron que el poder predictivo de las diversas variables económicas cambia a través del tiempo, de despreciable en la década de 1960 a significativo en la década de 1970. En 2000, Campbell resume los resultados hasta ese entonces (ver Tabla 1), estableciendo que "muchas de estas variables [predictoras] están relacionadas al estado del ciclo del negocio y predicen variaciones contra-cíclicas [Fama y French (1989), Lettau y Ludvigson (2001)]" (p. 1522).
En la última década, otros numerosos estudios han extendido los resultados previos, incluyendo los de Baker y Wurgler (2000), Lettau y Ludvigson (2001) -quienes relacionan la predictibilidad a la riqueza-, Cremers (2002), Avramov (2002), Goyal y Welch (2003) -quienes documentan solo predictibilidad usando razones de dividendo a rendimiento a la Campbell (2000)-, Cooper, Gutierrez Jr. y Marcum (2005) -quienes examinan la predictibilidad vía un portafolio simulado en tiempo real-, Guo (2006), Guo y savickas (2006) , santos y Veronesi (2006), Ang y Bekaert (2007), Cochrane (2008) y Campbell y Thomson (2008). Al mismo tiempo otros artículos, como el examen integral de la literatura previa fuera de la muestra por Goyal y Welch (2008) o por Cooper y Gulen (2006), impugnan la predictibilidad hallada en muchos de estos estudios, aunque Han (2010), por ejemplo, encuentra ganancias económicamente significativas incluso cuando en algunos casos no puedan ser estadísticamente significativas.

Muchos de estos artículos anteriores establecen la predictibilidad de diferentes maneras. Por ejemplo, Goyal y Welch (2008, p. 1455) escriben: "la literatura es difícil de absorber. Diferentes artículos usan técnicas, variables y periodos de tiempo diferentes". Sin embargo, en su revisión integral ellos estudian básicamente la siguiente ecuación
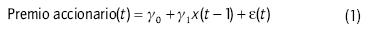
donde x es un vector de variables independientes.
Las variables x más prominentes exploradas en la literatura son la razón dividendo precio y el rendimiento del dividendo, la razón ganancias precio y la razón dividendo ganancias (razón de pago), varias tasas de interés y brechas, la tasa de inflación, la razón libro a mercado, la volatilidad, la razón inversión capital, la razón del consumo, riqueza e ingreso, y la actividad de emisión agregada neta o de acciones (Goyal y Welch, 2008, p. 1455).
La predictibilidad se establece, por ejemplo, por medio del R2(ajustado) del modelo y de la significancia de Yi donde " Y1 se interpreta como la medida de cuán significativo es x al predecir el premio accionario" (Goyal y Welch, 2008, sin embargo, en prácticamente ninguno de estos trabajos citados previamente la predictibilidad es medida per se; el término predictibilidad se refiere al hecho de que los predictores en la regresión explican parcialmente la varianza de los retornos esperados. El objetivo de este trabajo es utilizar diversas metodologías para medir directamente una predictibilidad "instantánea" que varía en el tiempo, al igual que establecer posibles determinantes económicos y financieros. La predictibilidad dinámica (que varía en el tiempo) permite no solo describir mejor el fenómeno de la predictibilidad, sino que también permite construir algoritmos que predicen mejor y que pueden superar la estrategia de comprar y mantenerse incluso teniendo en cuenta los costos de transacción, como mostramos cerca dei final de este trabajo. Entre las medidas exploradas, la medida de predictibilidad de mayor rentabilidad encontrada fue el valor p del test de la razón de varianzas. De hecho, se halló evidencia de que existe una relación entre esta predictibilidad y varios fundamentales financieros y económicos. Los resultados de este estudio sugieren que la predictibilidad evoluciona dinámicamente en el tiempo.
El artículo está conformado de la siguiente manera. La sección que sigue introduce los datos y las tres medidas de predictibilidad diferentes que vamos a usar. Posteriormente, se muestran los resultados respectivos de la medición de la predictibilidad dinámica; esta sección también desarrolla algunos algoritmos de predicción basados en las medidas de predictibilidad y examina si generan más dinero que la estrategia de comprar y mantenerse. Igualmente, relaciona la medida más promisoria en términos de rentabilidad con diversas variables económicas y financieras. En la última sección se resume y concluye.
Medidas de predictibilidad
Datos
Los datos objeto de este estudio los constituyen los rendimientos diarios (log-retornos) del índice S&P 500 desde el 3 de enero de 1950 hasta el 31 de diciembre de 2010. Para medir la predictibilidad instantánea usamos las tres medidas de predictibilidad que se describen a continuación en esta misma sección en una ventana móvil de 252 días de ancho, que se mueve de diez en diez días (ver Figura 1). La primera medida, la medida eta, intenta medir qué tanto es capaz de captar un modelo (a saber, una red neuronal) los patrones en los rendimientos. Si no hay patrones, la predicción de los retornos se comporta de forma parecida a la predicción de ruido (los retornos permutados), y la medida eta es capaz de detectar esta ausencia de patrones. Las otras dos medidas de predictibilidad, basadas en el test de la razón de varianzas y en el análisis de fluctuación sin tendencia, utilizan una propiedad del proceso de camino aleatorio y de la difusión asociada a él (a saber, la linealidad de la varianza en el tiempo) para detectar si los incrementos o decrementos de los rendimientos están correlacionados (si tienen memoria). Si no hay memoria, los retornos son impredecibles.
Medida eta
Trabajos precursores que propusieron medidas de predictibilidad de una serie de tiempo incluyen conceptos tan tempranos como el horizonte de la varianza de la predicción de Parzen (1982) y el test F de este horizonte por Oller (1985), y tan recientes como los de Diebold y Kilian (2001) y Galbraith (2003).
En su libro, Granger y Newbold (1986) usan una medida de la predictibilidad de una serie de covarianza estacionaria similar al R2de una regresión lineal:
donde rtes el retorno en el tiempo 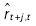 es la predicción óptima (i.e. la media condicional) y
es la predicción óptima (i.e. la media condicional) y 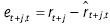 . De forma similar, se halla en Galbraith (2003) la función de contenido de la predicción
. De forma similar, se halla en Galbraith (2003) la función de contenido de la predicción
donde  es la media muestral,
es la media muestral,  es la predicción s-pasos hacia adelante y MSB denota el error cuadrático medio.
es la predicción s-pasos hacia adelante y MSB denota el error cuadrático medio.
Diebold y Kilian (2001) proponen una medida más general de la cual la medida de Granger y Newbold (1986) es un caso especial2
donde E es la esperanza matemática condicional al conjunto de información 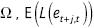 es la pérdida condicional esperada de una predicción óptima de corto plazo y
es la pérdida condicional esperada de una predicción óptima de corto plazo y  esla pérdida de una predicción óptima de largo plazo. Esta medida es similar a la estadística U de Theil, siendo la mayor diferencia el que la U de Theil evalúa la predicción real respecto a una predicción "inocente" sin cambios, mientras que P la evalúa respecto a la predicción de k-pasos. "Para ver esto, [se debe] establecer P en el caso cuadrático, univariado, con j = 1 y escribirla como P(cuadrático, univariado,
esla pérdida de una predicción óptima de largo plazo. Esta medida es similar a la estadística U de Theil, siendo la mayor diferencia el que la U de Theil evalúa la predicción real respecto a una predicción "inocente" sin cambios, mientras que P la evalúa respecto a la predicción de k-pasos. "Para ver esto, [se debe] establecer P en el caso cuadrático, univariado, con j = 1 y escribirla como P(cuadrático, univariado, 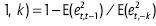 o
o  (véase Diebold y Kilian, 2001, p. 659).
(véase Diebold y Kilian, 2001, p. 659).
Generalizando a Diebold y Kilian (2001) e inspirado en Kaboudan (2000), usamos la siguiente definición de predictibilidad: sea  una serie de log-retornos y
una serie de log-retornos y  la misma serie con los valores permutados al azar. La predictibilidad de r con respecto al conjunto de predictores F bajo la metodologia M viene dada por
la misma serie con los valores permutados al azar. La predictibilidad de r con respecto al conjunto de predictores F bajo la metodologia M viene dada por

donde

con  como el valor predicho de rt j-pasos hacia adelante y
como el valor predicho de rt j-pasos hacia adelante y 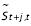 como el valor predicho de st j-pasos hacia adelante bajo la metodologia M usando el conjunto de predictores F. Así, en lugar de comparar la predicción a corto plazo vs. Largo plazo, como en Diebold y Kilian (2001), comparamos la predicción real vs. Una predicción de la misma serie permutada. Más precisamente, la medida de predictibilidad introducida compara el rendimiento de un predictor j-pasos hacia adelante de la serie original y la permutada bajo la metodologia M (por ejemplo, redes neuronales o programación genética) usando el conjunto de predictores F (por ejemplo, rezagos de r o variables macroeconómicas)3.
como el valor predicho de st j-pasos hacia adelante bajo la metodologia M usando el conjunto de predictores F. Así, en lugar de comparar la predicción a corto plazo vs. Largo plazo, como en Diebold y Kilian (2001), comparamos la predicción real vs. Una predicción de la misma serie permutada. Más precisamente, la medida de predictibilidad introducida compara el rendimiento de un predictor j-pasos hacia adelante de la serie original y la permutada bajo la metodologia M (por ejemplo, redes neuronales o programación genética) usando el conjunto de predictores F (por ejemplo, rezagos de r o variables macroeconómicas)3.
El siguiente caso especial con función de pérdida cuadrática L(e) = e2y j = 1 provee un ejemplo donde la esperanza ha sido reemplazada por un momento muestral por razones computacionales: SSEr

donde SSE son las siglas de la suma de los errores cuadráticos, esto es:

Una alternativa más complicada es la siguiente:

Nótese que cuando la serie r es determinista, SSEr = 0, y η1 = η2= 1. Por otro lado, cuando la serie r no es predecible, permutarla es irrelevante, SSEr = SSES, y η1= η2 = 0. Mientras que Kaboudan (2000) usa η2 que resulta en valores en un intervalo pequeño para las series de tiempo financieras, Duan (2002) sugiere η2 para mejorar la resolución de la métrica (i.e. para tener valores de η2 en un intervalo más grande). En este estudio, hacemos uso de la medida η1. Modificaciones de la medida η1 de Kaboudan (que no vamos a usar) pueden encontrarse en Abbas y Arif (2006) y Teodorescu y Fira (2008). Por supuesto, también existen otras aproximaciones a la predictibilidad (especialmente desde la física); por ejemplo, las de Salvino, Cawley, Grebogi y Yorke (1995), Molgedey y Ebeling (2000) y Qian y Rasheed (2004).
La metodologia M escogida es una red neuronal "feedforward" que utiliza como conjunto de predictores F tres rezagos de los log-retornos, dos rezagos del volumen diferenciado, dos rezagos del precio de apertura diferenciados y dos rezagos de la razón del precio diario más alto al precio diario más bajo. El modelo neuronal usado es un sistema neural ARX que son las siglas de AutoRegresivo con señal de entrada eXtra. El modelo predictor puede describirse con la siguiente ecuación:

donde la función 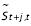 es la predicción de la señal de salida, la función g es el modelo de red neuronal, Q representa los parámetros del modelo y xtson los regresores del modelo. El regresor está dado por la siguiente entrada:
es la predicción de la señal de salida, la función g es el modelo de red neuronal, Q representa los parámetros del modelo y xtson los regresores del modelo. El regresor está dado por la siguiente entrada:

donde r es el log-retorno, u1 es la razón precio más alto a precio más bajo, u2es el logaritmo del precio de apertura diferenciado y u3es el volumen diferenciado. La escogencia de las variables de entrada fue el resultado de seleccionar por ensayo y error un regresor prometedor. El vector de entrada, o vector regresor, como es llamado a menudo en conexión a los sistemas dinámicos, contiene valores de entrada y de salida rezagados del sistema especificado por tres indices: na, nby nk. Para un modelo MISO (multiple input, single output) el vector de entrada se ve así:
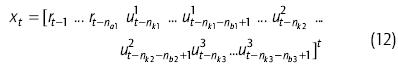
El índice narepresenta el número de valores de salida rezagados; a menudo se le llama orden del modelo. El indice nkes el retraso de la entrada respecto a la salida. El índice nb representa el número de valores de entrada rezagados. Para nuestro modelo ARX, tenemos na = {3}, nb = {2,2,2}, y nk = {1,1,1}. En nuestro modelo ARX, usamos dos neuronas ocultas en la red neuronal "feedforward". Específicamente, la red tiene 9 entradas y 1 salida, y consiste de una capa oculta con dos neuronas con función de activación de tipo sigmoideo. La red tiene un submodelo lineal. Para la red neuronal que se utilizó, usamos 202 días de entrenamiento y 50 días de validación, moviendo la ventana de 252 días cada diez días.
La hipótesis del camino aleatório y el test de la razón de varianzas
Otra posibilidad para medir la predictibilidad de una serie de tiempo es a través de una comparación sistemática con el camino aleatorio que no es predecible. Dada una serie de tiempo en niveles (logarítmicos)  , la hipótesis del camino aleatorio corresponde al modelo AR
, la hipótesis del camino aleatorio corresponde al modelo AR
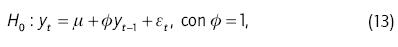
donde µ es el parámetro de deriva y las innovaciones εt no son, en general, ni independientes ni idénticamente distribuidas (pero 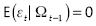 , donde Ωt-1 es la información hasta t - 1). Campbell, Lo y MacKinlay (1997) se refieren al proceso de camino aleatorio en el cual las innovaciones no son i.i.d. (y no están correlacionadas) como la hipótesis del camino aleatorio 3 (RW3).
, donde Ωt-1 es la información hasta t - 1). Campbell, Lo y MacKinlay (1997) se refieren al proceso de camino aleatorio en el cual las innovaciones no son i.i.d. (y no están correlacionadas) como la hipótesis del camino aleatorio 3 (RW3).
Uno de los tests de RW3 es llamado el test de la razón de varianzas (VR) (cf Campbell et al, 1997). El test VR explota el hecho de que en un camino aleatorio la varianza muestral del retorno en el k-periodo yt- yt-kes k veces la varianza muestral del retorno de un periodo yt- yt-1. La razón de varianzas puede definirse como

donde pies el coeficiente de autocorrelación i-ésimo de rt = yt - yt-1. La idea principal del test VR es que para el camino aleatorio Var(yt - yt-k) = kVar(yt -yt-]), es decir, V(k) = 1. El test VR puede pensarse entonces como un test de la hipótesis conjunta ft =... = pk-1 = 0, i.e. de que los retornos no estén correlacionados.
Un test específico puede construirse usando un estimador de V(k). Así, por ejemplo, está el estimador:

donde  es un estimador de la varianza del retorno del periodo uno usando retornos de un periodo, i.e. rt, y está definido como:
es un estimador de la varianza del retorno del periodo uno usando retornos de un periodo, i.e. rt, y está definido como:

donde 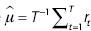 . Hay varias formas de definir
. Hay varias formas de definir  una de ellas, llevada a cabo contando con retornos en horizontes largos que se traslapan (k-periodos), es la siguiente:
una de ellas, llevada a cabo contando con retornos en horizontes largos que se traslapan (k-periodos), es la siguiente:
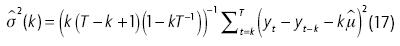
que es un estimador no sesgado de la varianza del retorno en el k-periodo cuando σ2t es constante en el tiempo.
Para tener en cuenta la heteroscedasticidad condicional, Lo y MacKinlay (1988) sugieren la estadística de la razón de varianzas:

que sigue asintóticamente una distribución normal bajo H0, donde
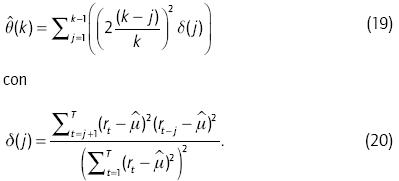
Para medir la predictibilidad instantánea, calculamos el valor p usando una ventana deslizante de 252 días de ancho que se mueve cada diez días. Ya que hay una razón de varianzas para cada valor de k, se puede evaluar la estadística para, por ejemplo, todos los valores de k entre 2 y 10, y calcular un estadístico del test conjunto que es el máximo valor absoluto del conjunto de estadísticos de la razón de varianzas múltiple, como en Chow y Denning (1993). El valor p para el estadístico de Chow-Denning usando m estadísticos de la razón de varianzas está acotado por arriba por la probabilidad de la distribución del módulo máximo de Student (SMM), con parámetro m y T grados de libertad.
Tanto en los estadísticos de Lo y MacKinlay (1988) como en el de Chow y Denning (1993) se usa la distribución límite cuando T → ∞ para aproximar los valores p. Kim (2006), por otra parte, ofrece una aproximación de "wild bootstrap" para mejorar las propiedades de muestra pequena de los tests de razón de varianzas. La aproximación involucra calcular el estadístico del test de la razón de varianzas individual (Lo y MacKinlay, 1988) o conjunto (Chow y Denning, 1993) en muestras de observaciones formadas al darle pesos a los datos originales por medio de variables aleatorias de media 0 y varianza 1, y usar los resultados para formar distribuciones "bootstrap" de los estadísticos del test.
En particular, la aproximación de "wild bootstrap" se hace en tres etapas:
1. Formar una muestra "bootstrap" de T observaciones 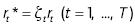 donde ζt es una sucesión aleatoria normal con
donde ζt es una sucesión aleatoria normal con  .
.
2. Calcular AVR *(k), la estadística VR obtenida de 
3. y repetir (1.) y (2.) B veces para formar la distribución "bootstrap"  (vide Kim, 2006).
(vide Kim, 2006).
En este estudio usamos 1.000 repeticiones del peso aleatorio que sigue la distribución normal estándar para completar el "bootstrap" para cada ky reportamos el valor p de Chow y Denning. Los valores p de "bootstrap" se calculan directamente de la fracción de réplicas que caen afuera de los límites definidos por el estadístico estimado originalmente.
Análisis de fluctuación sin tendencia y exponente de Hurst
Aún otra posibilidad para determinar la predictibilidad de una serie es el análisis de fluctuación sin tendencia. El análisis de fluctuación sin tendencia (DFA) (Peng, Buldyrev, Havlin, Simons, Stanley y Goldberger, 1994) permite distinguir entre la difusión normal y la anómala. En el caso de la difusión clásica, el segundo momento es lineal con el tiempo, mientras que los procesos de difusión anómala exhiben desviaciones específicas de esta propiedad fundamental. En particular, la subdifusión está caracterizada por  y la superdifusión por
y la superdifusión por 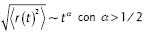 .
.
El análisis de fluctuación sin tendencia ha probado ser un estimador confiable del exponente a; por esta razón vamos a enfocarnos en ese método solamente4. Vale la pena mencionar que en el movimiento browniano fraccional, a no es otra cosa que H, el así llamado exponente de Hurst, que ha sido relacionado con la predictibilidad por varios estudios empíricos. Por ejemplo, Qian y Rasheed (2004) encontraron por medio de redes neuronales que entre más por encima de 1/2 resulta el exponente de Hurst de una serie financiera, mayor es la predictibilidad de la serie.
El DFA (con cajas que no se traslapan) se obtiene por medio de cuatro pasos. Comenzamos con la serie de log-retornos  . En el primer caso, calculamos la serie acumulada
. En el primer caso, calculamos la serie acumulada

con

En el segundo paso, dividimos Yt en  segmentos (o cajas) que no se traslapan de igual longitud r, donde
segmentos (o cajas) que no se traslapan de igual longitud r, donde  denota la función piso. En el tercer paso, calculamos la tendencia lineal local de cada segmento
denota la función piso. En el tercer paso, calculamos la tendencia lineal local de cada segmento  por medio de un ajuste de mínimos cuadrados,
por medio de un ajuste de mínimos cuadrados,

con valores sobre t = vτ +1, . . . ,vτ + τ para cada v. Finalmente, calculamos la función de fluctuación reescalada definida como
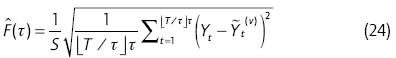
donde

Aquí hemos usado la definición de fluctuación hallada en Vasconcelos (2004) (adaptando la notación y corrigiendo el error tipográfico)5. Esta definición es muy similar a otras definiciones estándar de la función de fluctuación excepto por el factor de escala 1/S y por el número total de observaciones a ser consideradas (cf. Ausloos, 2000; Kantel-hardt, Koscielny-Bunde, Rego, Havlin y Bunde, 2001).
Un exponente generalα puede obtenerse usando la fórmula

donde C es una constante independiente de τ. En un gráfico doble-logarítmico la relación genera una línea recta cuya pendiente es precisamente el exponente α , y así la regresión lineal log 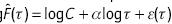 produce inmediatamente a. Para calcular el exponente α dinámico local, usamos una ventana deslizante de 252 días de ancho que se mueve cada diez días.
produce inmediatamente a. Para calcular el exponente α dinámico local, usamos una ventana deslizante de 252 días de ancho que se mueve cada diez días.
Para interpretar el exponente a , se puede recurrir al movimiento browniano fraccional (fBm) en el cual a es el exponente de Hurst H. Valores de 1/2 < H < 1 indican incrementos del fBm correlacionados positivamente y valores de 0 < H < 1/2 indican incrementos del fBm correlacionados negativamente, mientras que H = 1/2 implica incrementos estadísticamente independientes. La elección del fBm para la interpretación puede considerarse algo restrictiva, pero, más ampliamente, las medidas empíricas de exponentes a , tales como las obtenidas a través de DFA, mostrando adicionalmente que los incrementos son estacionarios o que la dinámica realmente tiene memoria, pueden ser interpretadas como evidencia de autocorrelaciones dentro de los datos (Bassler, Gunaratne y McCauley, 2006).
Resultados
Medida eta
La medida eta sugiere la presencia de predictibilidad, especialmente durante las décadas de 1950 y 1960. Para facilitar la comparación con los periodos "poco predecibles", se muestran los percentiles 90 y 95 de la medida eta para la serie permutada en la Figura 2.
Test de la razón de varianzas
Respecto al test de la razón de varianzas conjunta para k = 2 a 10 (Chow y Denning, 1993), usando "wild bootstrap" para tomar en cuenta los efectos de tamaño finito (Kim, 2006), hay una desviación significativa de la hipótesis nula de camino aleatorio especialmente en el periodo 1967-1978 (Figura 3).
Para verificar la predictibilidad durante el periodo predecible 1967-1978, seleccionamos a discreción y comparamos dos modelos ARMA: un modelo ARMA en el periodo predecible 1967-1978 y un modelo ARMA durante el periodo normal no predecible 1985-2000. Los resultados son como se esperaba (ver Tabla 2): el modelo ARMA durante el periodo predecible tiene un RR = 0,076, mientras que el modelo similar (ARMA(3,2) con constante) durante 19852000 tiene coeficientes significativos pero un RR = 0,006. La diferencia en el coeficiente de determinación es similar cuando se escogen los modelos ARMA automáticamente de un conjunto de 25 modelos predeterminados (ARMA(i, j) con i = 0, ...,4 y j = 0, ...,4), mediante el criterio de información de Schwartz. De hecho, el mejor modelo ARMA durante el periodo no predecible según este criterio es un ARMA(0,0). El fuerte rechazo de la hipótesis del camino aleatorio durante un periodo cercano a una década es evidencia en contra de las expectativas racionales, y apunta a explicaciones basadas en agentes de racionalidad limitada tal como en la hipótesis del mercado adaptativo.
DFA y exponente α
Para medir el exponente a instantáneo, usamos una ventana deslizante de 252 días que se mueve cada 10 días. El exponente a general se obtiene usando la fórmula

por medio de una regresión en una muestra de (hasta 30) puntos igualmente espaciados en el rango de la coordenada logτ. Este procedimiento de muestreo acelera los cálculos. El resultado final está dado en la Figura 4 y sugiere predictibilidad incrementada intermitente, sobre todo en las décadas de 1960 y 1970.
Predicciones
Las tres medidas coinciden en presentar predictibilidad incrementada en ciertos periodos (especialmente antes de 1980). Basados en las medidas de predictibilidad, probamos si el índice S&P 500 podía ser predicho exitosamente. Básicamente, usamos la misma red neuronal que se utilizó para construir la medida eta para predecir fuera de la muestra durante 10 días de transacción después de cada fecha predecible. Una fecha predecible es una fecha en la que la medida de predictibilidad estaba fuera de la banda del percentil 90 (o tenía un valor p < 0,1) para uno de los métodos en particular. Primero, el algoritmo chequea si la fecha es parte de las fechas predecibles halladas por la medida dada (se construyó un algoritmo para cada medida). Segundo, si es afirmativa la respuesta, el algoritmo predice los valores del índice un día hacia adelante por los siguientes 10 días. Se calcula entonces lo que el algoritmo gana durante esos diez días, así: se suman los log-retornos reales de cada día predicho que tenía una predicción de log-retornos positiva (el algoritmo compra el índice en los días en que la predicción es positiva); a este valor se le añade la suma de los log-retornos del activo libre de riesgo para las fechas en las cuales la red neuronal predice un log-retorno negativo (el algoritmo vende el índice e invierte a la tasa libre de riesgo en los días en que la predicción es negativa). El número de veces que el algoritmo entra al mercado accionario también se computa y se usa para calcular los costos de transacción.
En suma, el algoritmo computa los retornos de 10 días a partir de una fecha predecible de la siguiente manera (cf. Lohpetch y Corne, 2010):
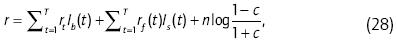
donde rtes el log-retorno, r;(t) es la tasa libre de riesgo en el día t, Ib(t) e Is(t) son funciones indicatrices, cada una igual a uno si el algoritmo señala comprar o vender, respectivamente, y cero de otra manera; n denota el número de transacciones (el número de señales de compra seguido de una subsecuente señal de venta), y c es el costo de transacción de una sola vía (como fracción porcentual del precio). Cuando la predicción de la red neuronal es positiva, las funciones indicatrices toman valores Ib (t) = 1 e Is(t) = 0, de otro modo Ib(t) = 0 e Is (t) = 1. En una fecha no predecible, el algoritmo está fuera del mercado por todos los diez días y el retorno es la suma de las tasas libres de riesgo en tales días.
La Tabla 3 resume los resultados. Para cada medida, se calculó el costo de transacción máximo para salir sin ganar ni perder. Como puede verse allí, las predicciones usando las fechas predecibles del test de la razón de varianzas permitieron un costo c de transacción tan alto como 0,15 por ciento para salir sin ganar ni perder, lo que es un costo razonable para un "trader" de piso. Esto muestra que el algoritmo puede implementarse para obtener ganancias, o al menos que esto fue históricamente cierto. Las otras medidas de predictibilidad no fueron tan efectivas. Las diferencias entre las medidas de predictibilidad pueden deberse a la eficiencia con que estas medidas detectan los patrones en la serie de retornos. Específicamente, el test de la razón de varianzas parece ser bastante potente estadísticamente para rechazar la hipótesis de ausencia de patrones en comparación con las otras medidas, probablemente por el detallado análisis estadístico que implica su construcción. Esta potencia estadística se traduciría en una mayor rentabilidad del algoritmo de inversión basado en él.
Relación de la predictibilidad con variables que miden valor
Para la medida de predictibilidad que permitía los mayores costos de transacción, a saber el valor p del test VR conjunto, se evaluó si esta medida de predictibilidad estaba asociada a variables que miden valor. El objetivo aquí es corroborar si la predictibilidad está asociada a variables económicas y financieras fundamentales. Las variables que miden valor que fueron consideradas son las siguientes6:
Dado que algunas variables eran diarias, otras mensuales y otras anuales, las variables fueron interpoladas para volverlas todas diarias como ilustra el siguiente ejemplo: si una variable es mensual, se le asigna el valor del mes al primer día hábil de ese mes, y este valor permanece constante hasta que cambia el mes, y de forma análoga para una variable anual. La motivación para el uso de estas variables es que, como miden el valor en la economía, pueden estar relacionadas con la predictibilidad del índice S&P 500, ya que el índice mide el valor de las principales empresas de la economía. En general, es muy difícil tratar de anticipar cómo depende la predictibilidad de estas variables.
Como las variables independientes presentaban un alto grado de multicolinealidad (como se evidenció en el número de condición y en los valores VIF), se realizó un análisis factorial con rotación Varimax para obtener "factores de valor" (ver Tabla 4). La medida de adecuación muestral de Kaiser-Meyer-Olkin (0,725) y la prueba de esfericidad de Bartlett (p < 0,01) corroboraron que el análisis factorial aplicaba. Al relacionar el valor p del test de la razón de varianzas con los factores7 se incluyeron todos los factores, ya que no se puede saber de antemano qué factores están más asociados con la variable dependiente.
El valor p del test VR conjunto dependió de doce factores, es decir, de todos menos del sexto y del décimo, al nivel de significancia del 10% con un R2adj = 0,37 (ver Tabla 5). Debido a la presencia de heteroscedasticidad y autocorrrelación, se usó el estimador robusto para los errores estándar HAC. El resultado obtenido parece sugerir firmemente que existe una relación entre valor y predictibilidad. Esta relación no es de sorprender ya que el índice S&P 500, como habíamos expresado con anterioridad, también es una medida de valor económico.
Discusión y conclusiones
La predictibilidad de las acciones ocupa un papel muy relevante en las finanzas, y las posiciones al respecto son contradictorias como lo atestiguan el uso del análisis técnico por los practicantes que intentan día a día predecir los precios de las acciones a corto plazo o el Premio Nobel de Economía de 2013 en cuyo comunicado de prensa se señala que "no hay manera de predecir el precio de las acciones y los bonos en los próximos días o semanas" (Nobelprize.org, 2013). Existe una amplia literatura sobre la predictibilidad, en especial utilizando variables exógenas. El presente estudio aborda la predictibilidad del índice S&P 500 desde 1950 a 2010 mediante tres medidas dinámicas de predictibilidad que intentan capturar los patrones de la serie per se, a saber, la medida eta, el valor p del test de la razón de varianzas y el exponente a del análisis de fluctuación sin tendencia. Para obtener medidas de predictibilidad que variaban en el tiempo (dinámicas), se utilizó una ventana deslizante de un año de ancho que se movía cada 10 días. Las medidas de predictibilidad señalaron la existencia de periodos agrupados de mayor y menor predictibilidad, lo que parece estar en línea con resultados previos sobre índices del mercado estadounidense similares (cf. Kim, Lim, y Shamsuddin, 2011; Urquhart y Hudsony, 2013)8. Por ejemplo, una observación que surgió es que existe evidencia de una impredictibilidad del mercado incrementada después de 1980. La década anterior, de 1968-1978, mostró predictibilidad, usando el test de la razón de varianzas conjunto para k = 2 a 10 (Chow y Denning, 1993) con "wild bootstrap" para tener en cuenta los efectos de tamaño finito (Kim, 2006) y esta predictibilidad incrementada fue confirmada por medio de regresiones ARMA. Es difícil establecer a qué se puede deber la desaparición de la predictibilidad en la década de 1980, pero candidatos podrían ser las varias innovaciones introducidas en el mercado (como la introducción del Sistema de Transacción Intermercado en 1978 o una gran actualización de tecnología en el piso de transacción en 19799), al igual que el inicio en la década de 1980 de la "gran moderación" en la que las variables financieras y económicas cambiaron menos que en el pasado.
Para ir más allá de la predictibilidad, las diferentes medidas de predictibilidad se compararon respecto a la rentabilidad que puede alcanzarse con predicciones basadas en ellas mediante un algoritmo que considera invertir solo cuando la predictibilidad (de acuerdo con cada medida) es alta. Típicamente los algoritmos de predicción intentan predecir la serie todo el tiempo, por lo que el tipo de algoritmo utilizado implica una innovación en cuanto al modo de predicción: si la serie tiene periodos más predecibles que otros, como hallamos en este trabajo, más vale no intentar predecirla cuando esta es impredecible. Las diferencias en los resultados de las medidas de predicción halladas se deben probablemente a diferencias en su capacidad de captar los patrones de la serie. Sin embargo, la rentabilidad del algoritmo para cada una de las tres medidas utilizadas excedió la rentabilidad de la estrategia de comprar y mantenerse. Para la medida del valor p del test de la razón de varianzas, es posible incluso implementar costos de transacción realistas (de, por ejemplo, 0,1%) y obtener una ganancia.
Al enfocarse en la medida con mayor rentabilidad, se halló igualmente evidencia de que existe una relación entre la predictibilidad y fundamentales financieros y económicos que miden valor. Para agrupar estos fundamentales, dada su colinealidad, se establecieron "factores de valor" mediante un análisis factorial, y la relación entre valor y predictibilidad se sostuvo en prácticamente todos los factores de acuerdo con una regresión lineal. Una línea de investigación prometedora es la de explorar más profundamente esta relación.
El panorama que arroja este estudio es el de un mercado que informacionalmente no es estáticamente predecible, sino cuya predictibilidad evoluciona dinámicamente en el tiempo. Este panorama es compatible con la hipótesis del mercado adaptativo (Lo, 2004) que implica que la predictibilidad cambia con las condiciones de mercado. Los tests de predictibilidad del mercado y los algoritmos de predicción en la literatura a menudo ignoran la naturaleza dinámica de la predictibilidad, o su dependencia del tipo de medida de predictibilidad utilizada, lo que contribuye a alcanzar resultados mixtos, y posiblemente al sesgo de "data snooping" (cf Kim, Lim y Shamsuddin, 2011).
Pie de página
1 Este trabajo ha sido financiando a través del proyecto CTIDA 2002/156 (Oficina de Ciencia y Tecnologia de la Generalitat Valenciana) titulado "Análisis estratégico de la fabricación y comercialización en la industria textil: aplicación de nuevas tecnologias". CTIDIA2002-156. PIGV - Projectes d'Investigació de la Consellería de Innovación y Competitividad de la Generalitat Valenciana.
2 Tenemos a la medida de Granger y Newbold (1986) como un caso especial,
"cuando la serie es de covarianza estacionaria, L (x) = x2 (y por
ende la predicción óptima es la media condicional), el conjunto de información
es univariado, y k = ∞" (Diebold y Kilian, 2001, p. 659).
3 Los predictores no se permutan, solo la serie.
4 De hecho, se ha dicho del DFA que es más confiable que el análisis R/S
de Hurst (Vasconcelos, 2004).
5 La definición de la población de la función de fluctuación reescalada
puede hacerse como  .
.
6 Las variables fueron extraídas del sitio MeasuringWorth.com y el CAPE de la página web de Robert J. Shiller http://www.econ.yale.edu/~shiller/. Las fechas de las recesiones fueron extraídas del National Bureau of Economic Research http://www.nber.org/cycles.html.
7 Se corroboró que los factores ya no eran multicolineales.
8 Verheyden, De Moor y Van den Bossche (2013) contienen, para comparación, una corta lista de otros trabajos con un énfasis en la predictibilidad dinámica, aunque con diferencias metodológicas y en los datos usados.
9 Ver http://www.nyse.com/about/history/timeline_1960_1979_index.html.
Referencias bibliográficas
Abbas, S. R., & Arif, M. (2006). New time series predictability metrics for nearest neighbor based forecasting. Congreso Multitopic Conference, 2006, INMIC06 (pp. 100-105). Islamabad: IEEE.
Ang, A., & Bekaert, G. (2007). Stock return predictability: Is it there? Review of Financial Studies, 20(3), 651-707.
Ausloos, M. (2000). Statistical physics in foreign exchange currency and stock markets. Physica A: Statistical Mechanics and its Applications, 285(1), 48-65.
Avramov, D. (2002). Stock return predictability and model uncertainty. Journal of Financial Economics, 64(3), 423-458.
Baker, M., & Wurgler, J. (2000). The equity share in new issues and aggregate stock returns. Journal of Finance, 55(5), 2219-2257.
Bassler, K., Gunaratne, G., & McCauley, J. (2006). Markov processes, Hurst exponents, and nonlinear diffusion equations: With application to finance. Physica A: Statistical Mechanics and its Applications, 369(2), 343-353.
Bekaert, G., & Hodrick, R. (1992). Characterizing predictable components in excess returns on equity and foreign exchange markets. Journal of Finance, 47(2), 467-509.
Bossaerts, P., & Hillion, P. (1999). Implementing statistical criteria to select return forecasting models: What do we learn? Review of Financial Studies, 12(2), 405-428.
Breen, W., Glosten, L., & Jagannathan, R. (1989). Economic significance of predictable variations in stock index returns. Journal of Finance, 44(5), 1177-1189.
Campbell, J. (1987). Stock returns and the term structure. Journal of Financial Economics, 78(2), 373-399.
Campbell, J. (2000). Asset pricing at the millennium. Journal of Finance, 55(4), 1515-1567.
Campbell, J., & Shiller, R. (1988a). The dividend-price ratio and expectations of future dividends and discount factors. Review of Financial Studies, 7(3), 195-228.
Campbell, J., & Shiller, R. (1988b). Stock prices, earnings, and expected dividends. Journal of Finance, 43(3), 661-676.
Campbell, J., & Thomson, S. (2008). Predicting excess stock returns out of sample: Can anything beat the historical average? Review of Financial Studies, 27(4), 1509-1531.
Campbell, J., Lo, A., & MacKinlay, A. (1997). The econometrics of financial markets. Princeton: Princeton University Press.
Chow, K., & Denning, K. (1993). A simple multiple variance ratio test. Journal of Econometrics, 58(3), 385-401.
Cochrane, J. (1991). Production-based asset pricing and the link between stock returns and economic fluctuations. Journal of Finance, 46(1), 209-237.
Cochrane, J. (2008). The dog that did not bark: A defense of return predictability. Review of Financial Studies, 27 (4), 1533-1575.
Cooper, M., & Gulen, H. (2006). Is time-series-based predictability evident in real time? Journal of Business, 79(3), 1263-1292.
Cooper, M., Gutiérrez Jr. R., & Marcum, B. (2005). On the predictability of stock returns in real time. Journal of Business, 78(2), 111-130.
Cremers, K. (2002). Stock return predictability: A Bayesian model selection perspective. Review of Financial Studies, 75(4), 1223-1249.
Diebold, F., & Kilian, L. (2001). Measuring predictability: Theory and macroeconomic applications. Journal of Applied Econometrics, 76(6), 657-669.
Duan, M. (2002). Time series predictability. (Tesis de maestría sin publicar). Marquette University, Milwaukee.
Fama, E., & French, K. (1988a). Permanent and temporary components of stock prices. Journal of Political Economy, 96(2), 246-273.
Fama, E., & French, K. (1988b). Dividend yields and expected stock returns. Journal of Financial Economics, 22(1), 3-25.
Fama, E., & French, K. (1989). Business conditions and expected returns on stocks and bonds. Journal of Financial Economics, 25(1), 23-49.
Fama, E., & Schwert, G. (1977). Asset returns and inflation. Journal of Financial Economics, 5(2), 115-146.
Ferson, W. (1989). Changes in expected security returns, risk, and the level of interest rates. Journal of Finance, 44(5), 1191-1217.
Ferson, W., & Harvey, C. (1991). The variation of economic risk premiums. Journal of Political Economy, 99(2), 385-415.
French, S., Schwert, G., & Stambaugh, R. (1987). Expected stock returns and volatility. Journal of Financial Economics, 79(1), 3-29.
Galbraith, J. (2003). Content horizons for univariate time-series forecasts. International Journal of Forecasting, 79(1), 43-55.
Goetzmann, W., & Jorion, P. (1993). Testing the predictive power of dividend yields. Journal of Finance, 48(2), 663-679.
Goyal, A., & Welch, I. (2003). Predicting the equity premium with dividend ratios. Management Science, 49(5), 639-654.
Goyal, A., & Welch, I. (2008). A comprehensive look at the empirical performance of equity premium prediction. Review of Financial Studies, 27(4), 1455-1508.
Granger, C., & Newbold, P. (1986). Forecasting economic time series. New York: Academic Press.
Guo, H. (2006). On the out-of-sample predictability of stock market returns. Journal of Business, 79(2), 645-670.
Guo, H., & Savickas, R. (2006). Understanding stock return predictability. FRB of St. Louis Working Paper (No. 2006-019B).
Han, Y. (2010). On the economic value of return predictability. Annals of Economics and Finance, 77(1), 1-33.
Harvey, C. (1989). Time-varying conditional covariances in tests of asset pricing models. Journal of Financial Economics, 24(2), 289-317.
Hodrick, R. (1992). Dividend yields and expected stock returns: Alternative procedures for inference and measurement. Review of Financial studies, 5(3), 357-386.
Jegadeesh, N. (1990). Evidence of predictable behavior of security returns. Journal of Finance, 45(3), 881-898.
Kaboudan, M. (2000). Genetic programming prediction of stock prices. Computational Economics, 76(3), 207-236.
Kantelhardt, J., Koscielny-Bunde, E., Rego, H., Havlin, S., & Bunde, A. (2001). Detecting long-range correlations with detrended fluctuation analysis. Physica A: Statistical Mechanics and its Applications, 295(3-4), 441-454.
Keim, D., & Stambaugh, R. (1986). Predicting returns in the bond and stock markets. Journal of Financial Economics, 77(2), 357-390.
Kim, J. (2006). Wild bootstrapping variance ratio tests. Economics Letters, 92(1), 38-43.
Kim, J., Lim, K., & Shamsuddin, A. (2011). Stock return predictability and adaptive markets hypothesis: Evidence from century-long US data. Journal of Empirical Finance, 78(5), 868-879.
Lamont, O. (1998). Earnings and expected returns. Journal of Finance, 53(5), 1563-1587.
Lettau, M., & Ludvigson, S. (2001). Consumption, aggregate wealth, and expected stock returns. Journal of Finance, 56(3), 815-849.
Lewellen, J. (1999). The time-series relations among expected return, risk, and book-to-market. Journal of Financial Economics, 54(1), 5-43.
Lo, A. (2004). Adaptive markets hypothesis: Market efficiency from an evolutionary perspective. Journal of Portfolio Management, 30(5), 15-29.
Lo, A., & MacKinlay, A. (1988). Stock market prices do not follow random walks: Evidence from a simple specification test. Review of Financial Studies, 7 (1), 41-66.
Lohpetch, D., & Corne, D. (2010). Outperforming buy-and-hold with evolved technical trading rules: Daily, weekly and monthly trading. En: C. Di Chio, A. Brabazon, M. Ebner, M. Farooq, A. Fink, J. Grahl, ... N. Urquhart (Eds.), Applications of Evolutionary Computation de Lecture Notes in Computer Science (Vol. 6025, pp. 171181). Berlin - Heidelberg: Springer.
Molgedey, L., & Ebeling, W. (2000). Local order, entropy and predictability of financial time series. The European Physical Journal B, 75(4), 733-737.
Nelson, W. (1999). Three essays on the ability of the change in shares outstanding to predict stock returns. (Tesis doctoral sin publicar). Yale University, New Haven.
Nobelprize.org. (2013). The Prize in Economic Sciences 2013 - Press release. Nobel Media AB 2013. Recuperado en marzo 17, 2014, de http://www.nobelprize.org/nobel_prizes/economic-sciences/laureates/2013/press.html.
Oller, L. (1985). How far can changes in general business activity be forecasted? International Journal of Forecasting, 7 (2), 135-141.
Parzen, E. (1982). ARARMA models for time series analysis and forecasting. Journal of Forecasting, 7 (1), 67-82.
Peng, C., Buldyrev, S., Havlin, S., Simons, M., Stanley, H., & Goldberger, A. (1994). Mosaic organization of DNA nucleotides. Physical Review E, 49(2), 1685-1689.
Pesaran, M., & Timmermann, A. (1995). Predictability of stock returns: Robustness and economic significance. Journal of Finance, 50(4), 1201-1228.
Pontiff, J., & Schall, L. (1998). Book-to-market ratios as predictors of market returns. Journal of Financial Economics, 49(2), 141-160.
Poterba, J., & Lawrence, H. (1988). Mean reversion in stock prices: Evidence and implications. Journal of Financial Economics, 22(1), 27-59.
Qian, B., & Rasheed, K. (2004). Hurst exponent and financial market predictability. Congreso 2nd IASTED international conference on financial engineering and applications (pp. 203-209). Cambridge, MA: ACTA Press.
Salvino, L., Cawley, R., Grebogi, C., & Yorke, J. (1995). Predictability in time series. Physics Letters A, 209(5-6), 327-332.
Santos, T., & Veronesi, P. (2006). Labor income and predictable stock returns. Review of Financial Studies, 79(1), 1-44.
Schwert, G. (1989). Why does stock market volatility change over time? Journal of Finance, 44(5), 1115-1153.
Teodorescu, H., & Fira, L. (2008). Analysis of the predictability of time series obtained from genomic sequences by using several predictors. Journal of Intelligent and Fuzzy Systems, 79(1), 51-63.
Urquhart, A., & Hudson, R. (2013). Efficient or adaptive markets? Evidence from major stock markets using very long run historic data. International Review of Financial Analysis, 28(1), 130-142.
Vasconcelos, G. (2004). A guided walk down Wall Street: An introduction to econophysics. Brazilian Journal of Physics, 34(3B), 1039-1065.
Verheyden, T., De Moor, L., & Van den Bossche, F. (2013). A tale of market efficiency. Review of Economic and Business Literature, 58(2), 139-156.