USING MAGNETIC MOMENTS TO UNVEIL THE NUCLEAR STRUCTURE OF LOW-SPIN NUCLEAR STATES
USANDO MOMENTOS MAGNÉTICOS PARA DEVELAR LA ESTRUCTURA NUCLEAR A BAJO ESPíN
Diego A. Torres
Departamento de Física, Universidad Nacional de Colombia, Bogotá, Colombia
Contacto: Diego A. Torres datorresg@unal.edu.co
(Recibido: 12/2011. Aceptado: 12/2011)
Cómo citar: Torres, D.A., Momento, 43, 44 (2012)
Abstract
The experimental study of magnetic moments for nuclear states near the ground state, I ≤ 2, provides a powerful tool to test nuclear structure models. Traditionally, the use of Coulomb excitation reactions has been used to study low spin states, mostly I = 2. The use of alternative reaction channels, such as α transfer, for the production of radioactive species that, otherwise, will be only produced in future radioactive beam facilities has proved to be an alternative to measure not only excited states with I > 2, but to populate and study long–live radioactive nuclei. This contribution will present the experimental tools and challenges for the use of the transient field technique for the measurement of g factors in nuclear states with I ≤ 2, using Coulomb excitation and α–transfer reactions. Recent examples of experimental results near the N = 50 shell closure, and the experimental challenges for future implementations with radioactive beams, will be discussed.
Keywords: g factors, Lifetimes, α–transfer reaction, Inverse kinematics, Transient field, DSAM
Resumen
El estudio experimental de momentos magnéticos en estados nucleares cercanos al estado base, con momentum angular total (o espín) I ≤ 2, proporciona una poderosa herramienta para contrastar modelos que tratan de describir la estructura nuclear. Tradicionalmente, excitaciones de Coulomb han sido utilizadas para el estudio de estados a bajo espín, principalmente I = 2. El uso de canales de reacción alternos, tales como reacciones de transferencia de partículas α, para la producción de isótopos radiactivos que, de otra forma, solo podrán ser producidas en arreglos experimentales futuros, han demostrado ser una alternativa para medir no solamente estados excitados con I > 2, sino que además permiten poblar y estudiar núcleos radiactivos con tiempos de vida largos. Este trabajo presentará las herramientas experimentales y los retos existentes en la medición de factores g haciendo uso de la denominada "Técnica de Campo Trasiente", para estados nucleares con I ≤ 2, haciendo uso de reacciones de Coulomb y de transferencia de partículas α. Se mostrarán algunos resultados experimentales recientes en núcleos en los alrededores de un número de neutrones N = 50 (capa cerrada), y se discutirán las dificultades experimentales existentes en la futura implementación de la técnica en arreglos experimentales que harán uso de haces radiactivos.
Palabras clave: factores g, tiempos de vida, reacciones de transferencia α, cinemática inversa, campo transiente, DSAM.
Introduction
The knowledge of magnetic moments (μ(I)) in nuclear states is pivotal to obtaining a microscopic description of the nuclear wave function for the states under study. The use of the so–called Transient Field technique (TF), in inverse kinematic, has been successfully used for measuring μ(I) mostly in nuclear states with total angular momentum equal to 2![]() (from now on we will use the letter I for the total angular momentum of the nucleus in units of
(from now on we will use the letter I for the total angular momentum of the nucleus in units of ![]() ). In recent years, measurements on states with spins I > 2 have presented the opportunity to test some nuclear structure models in the A ~ 100 region [1–3]. A systematic study of such excited states will improve the quality of those models, but there is a lack of information on μ(I) values for I > 2, as can be seen in Figs. 1 and 2, where a compilation of g(2+1) and g(4+1) values for some nuclei around the N = 50 shell closure are presented.
). In recent years, measurements on states with spins I > 2 have presented the opportunity to test some nuclear structure models in the A ~ 100 region [1–3]. A systematic study of such excited states will improve the quality of those models, but there is a lack of information on μ(I) values for I > 2, as can be seen in Figs. 1 and 2, where a compilation of g(2+1) and g(4+1) values for some nuclei around the N = 50 shell closure are presented.
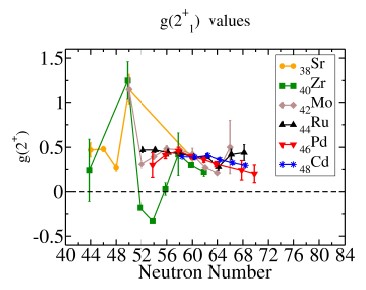
Figure 1. Experimental g(2+1) results for nuclei around the N = 50 magic number.
The evolution of nuclear collectivity, from spherical to deformed nuclei, has been recently reviewed for g(2+1) factors in heavy (A > 90) even–even nuclei [4]. A description of the N dependence of g factors in transitional nuclei is described using microscopic calculations with the tidal–wave model of Frauendorf and collaborators [5]. The calculated g factors are in overall agreement with the experiment, explaining the deviations from the Z/A values, and contributions from h11/2 neutrons explain the general decrease of g factors along the isotopic chains. Frauendorf also made predictions for g(4+1) values in the region. These authors pointed out the importance of measuring g(4+1) values to decisively contrast their model prediction with other models and test its prediction of g(2+1) > g(4+1) for most of the studied isotopes. The description of the use of the TF technique to study μ(I) in states with I ≥ 2 is one of the objectives

Figure 2. Experimental g(4+1) results for nuclei around the N = 50 magic number. The upcoming years should see an increase in the study of magnetic moments for states I > 2, as well as the increase in the precision of the measurements.
of this contribution. The experimental methods described are applicable to nuclei that can be used as a beam, or these experiments can produce new nuclear species with the transfer of α particles from the target to the beam. Some recently reported results will be briefly presented at the end of this contribution.
g–factor measurements
The basis of all g–factor measurements ![]() with μN the nuclear magneton) is the quantification of the nuclear spin precession angle (Δθ) caused by the interaction of a magnetic field (B) with the nuclear magnetic moment. For states with short lifetimes τ (of the order of picoseconds) the transient field technique has been successfully used in the past decades [6]. The Transient Field effect was first reported in 1968, by Borchers and collaborators, in nuclear magnetic moment measurements of ions when implanted in ferromagnetic materials [7]. An anomalous precession was only observed before the ions came to a stop inside the ferromagnetic host material. That let to the name "transient". It was suggested that the observed field is a hyperfine field originating from electrons in the atomic shell of the moving ion.
with μN the nuclear magneton) is the quantification of the nuclear spin precession angle (Δθ) caused by the interaction of a magnetic field (B) with the nuclear magnetic moment. For states with short lifetimes τ (of the order of picoseconds) the transient field technique has been successfully used in the past decades [6]. The Transient Field effect was first reported in 1968, by Borchers and collaborators, in nuclear magnetic moment measurements of ions when implanted in ferromagnetic materials [7]. An anomalous precession was only observed before the ions came to a stop inside the ferromagnetic host material. That let to the name "transient". It was suggested that the observed field is a hyperfine field originating from electrons in the atomic shell of the moving ion.
The relation between the g factor and the spin precession angle is given by:
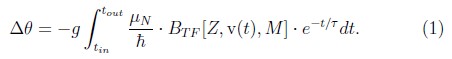
where the integral on the right side is equivalent to the calculation of Δθ when g = 1 (Δθ(g = 1)). This part is estimated using a parametrization of the transient magnetic field (BTF) which depends on the speed (v(t)), on the atomic number (Z) of the projectile ion, and on the magnetization (M) of the ferromagnetic layer of the target. The time dependence of v(t) is estimated according to the kinematic conditions of the experiment in conjunction with the slowing down of the ion in the target; tin and tout are the mean entrance and exit time, respectively, of the ions into, and out of, the ferromagnetic layer of the target. The term Δθ on the left side of Eq. (1) is called the experimental "spin precession effect"; this term is measured during the experiment from changes in the γ–ray angular distribution under two different BTF directions. The final g–factor value will be ![]() .
.
The transient Field BTF
The precession angle Δθ in Eq. (1) can be determined experimentally with a precision of milliradians with a modern detection system. For states with τ of the order of picoseconds, a magnetic field of the order of kilo–Tesla is needed to achieve this angular resolution. In the TF technique the field BTF[Z, v(t),M] originates from the spin of mainly single s electrons in the ions. This self–interaction has been parametrized as a function of M of the ferromagnetic material in the target, the speed of the ion inside the ferromagnet, and the Z of the ion. One such parametrization is the so–called Rutgers parametrization [8]

where M is given in Tesla and v0 = c/137 the Bohr velocity. This parametrization was obtained from measurements on a variety of nuclei from O to Pb whose magnetic moments had been obtained in experiments utilizing other techniques. A reevaluation of the parametrization would be worthwhile, if new independent moment measurements were available. Unfortunately, the data of reference [8] were taken decades ago and have relative large errors.
Another important step would be a theoretical description of BTF from first principles. Such a new description would improve, and unify, the existing parametrizations [6]. The studies should involve the collective efforts of the solid state and the nuclear structure fields, to include the use of several ferromagnetic materials, and may explore the use of fabricated ferromagnetic materials, with a well known magnetization, in a new generation of targets.
The target and the experimental setup
A multilayered target is the heart of a g–factor measurement experiment. In Fig. 3 a schematic view of the experimental setup is shown. In Fig. 4 the use of a target with two different reactions, Coulomb excitation and α transfer, is presented. The target can be also utilized to perform lifetime measurements using the Doppler Shift Attenuation Method (DSAM). Lifetimes are used for the evaluation of Eq. (1).
The fabrication of multilayered targets is an art that requires high levels of expertise. A typical Gd target, like the one utilized to obtain the results presented below, is made of ~ 0.5 mg/cm2 natural carbon deposited on a ~ 3.6 mg/cm² gadolinium layer, evaporated on a ~1.6 mg/cm² tantalum foil, backed by a 4.2 mg/cm² copper layer; the latter is the hyperfine–interaction-free material. Thin (~ 5.0 µg/cm2) layers of natural titanium are added between the carbon and gadolinium target layers, and also between the tantalum and copper, to provide good adherence of these elements to each other. References [13–15] are dedicated to the fabrication of these special targets.
The use of gadolinium in the target provides an excellent ferromagnetic environment with high M and lower stopping power, but liquid nitrogen must be used to keep the target below the Curie temperature. In recent years, several efforts have been implemented to study [16] and control fluctuations of the magnetization produced by temperature gradients originated by the beam spot on the target;
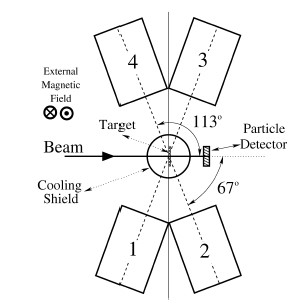
Figure 3. Upper view of the experimental setup used in a typical TF experiment. Gamma–ray detectors i = 1, 2, 3, and 4, are placed at angles at which the angular distribution of the γ–rays is pronounced; a particle detector is located downstream from the target. An external magnetic field (Bext = 0,07 T) is used to align and control the direction of BTF . The γ–ray photo peak intensity registered in the γ–ray detector i is a function of the direction of BTF (Up N↑i and Down N↓i).
one of the approaches to deal with this effect is the use of a cooling shielding placed around the target [1]. A more systematic study of this effect may explain the discrepancies encountered in the measured values of the g(2+1) of 106Pd [16], which provides one of the calibration points used by several BTF parametrizations.
The spin precession angle
The precession angle, Δθ in Eq. (1), for a given state, is obtained from the ratio of the precession effect (ε) over the logarithmic slope (S) of the angular correlation W)θγ), they are defined, respectively, as


Figure 4. a) and b) present a view of the target and two different population mechanisms, which occurs in the 12C layer. In a(: a Coulomb excitation reaction, the most widely used. The Coulomb interaction populates from the ground state the 2+1 level and subsequently the 4+1 levels (and even more states depending on the nucleus). The nuclear spin of the populated state precesses in the ferromagnetic layer and finally decays in the hyperfine–interaction–free cooper backing. The traversal time trough the layers is ~ 0.05 ps in the C layer and ~ 0.5 ps in the Gd layer. The detection of a carbon particle in coincidence with a γ–ray of the appropriate energy, ensures that the states under study actually originates in the carbon layer, and precesses in the ferromagnetic (Gd) material of the target. In b): an α–transfer reaction, α particles from the carbon layer are transferred to the 96Ru ion beam nuclei, producing radioactive 100Pd nuclei in excited states. The nuclei are excited into higher energy levels and decay to the lower states while traversing the Gd layer. A feeding correction must be applied [1, 3, 9–12[.
in Eq.(3) ![]() where N↑i (N↓i) is the γ–ray peak intensity measured at detector i when the external magnetic field, Bext, is up (down). The logarithmic slope, S(θγ), is evaluated at the angle θγ in the rest frame of the γ–ray emitting nuclei where W(θ) is more pronounced, usually at θγ = ± 67°. Several techniques can be used to obtain a reasonable logarithmic slope [6].
where N↑i (N↓i) is the γ–ray peak intensity measured at detector i when the external magnetic field, Bext, is up (down). The logarithmic slope, S(θγ), is evaluated at the angle θγ in the rest frame of the γ–ray emitting nuclei where W(θ) is more pronounced, usually at θγ = ± 67°. Several techniques can be used to obtain a reasonable logarithmic slope [6].
Two important conditions must be fulfilled to ensure a good Δθ measurement: a well defined precession effect, ε, with a minimum of around thousand counts per detector per field direction (N↑i); and a good angular correlation W(θ) measurement. Both conditions present serious limitations to future applications using radioactive beams, due to low yield and the presence of contaminants from the decay of the products.
Some results for the A ~ 100 region
In Fig. 5 a comparison of W (θ) for the 21+ → 01+ γ–ray transitions obtained in a Coulomb excitation reaction for 96Ru, and for the α–transfer partner reaction which produces 100Pd in excited states [1], is shown. A better alignment and more pronounced precession effect in the Coulomb excitation reaction is obtained, in comparison with the α–transfer reaction. These differences influence the final errors of the g–factor values, with g(2+1 = 0,46 (3) for 96Ru and g(21+) = 0,30 (14) for 100Pd [2]. Despite the apparent poor precision of the results for the 100Pd nucleus, the g factors of the 21+, 41+ and 61+ states were measured for the first time (see Fig. 6), and a collective behavior for the 21+ and 41+ states was reported.
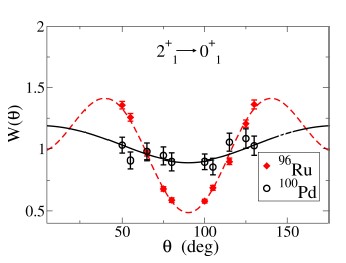
Figure 5. Comparison between the angular correlation of the experimental γ–ray angular correlations, W(θ), for the 21+ → 01+ transitions of 100Pd (circles) and 96Ru (diamonds). The solid and dashed lines correspond to fits to the angular correlation function for 100Pd and 96Ru, respectively.
An uncorrected value of g(100Pd; 61+) = 1,47(87) was obtained. In Fig. 6 results for 96Ru are also presented; the experimental trend

Figure 6. Results for the g factors of the 21+ and 41+ states for the radioactive 100Pd [1] nucleus and the 96Ru [2] nucleus. The experimental values are compared with theoretical predictions. For the 100Pd nucleus the results exclude the single–particle (Shell Model) behavior, while for 96Ru some additional theoretical efforts are necessary to explain the g factor trend as a function of the spin.
of g (21+) < g(24sub>1+) is not well accounted by two different shell–model calculations which predict g(21+) > g(41+) [2, 17].
In Ref. [3] the experimental study of the g factors for excited states, including 4+1, 2+1, and 3+1, were reported for the first time in 88Zr and 84,86,88Sr. Excited states in 88Zr were populated using an α transfer to ion beams nuclei of 84Zr. A negative value of g(86Sr; 4+1) = —0.68(49) is obtained, in contrast with the positive values g(86Sr; 2+1) = 0,285(14) and g(88Zr; 4+1) = +0.65(18). This result needs additional theoretical efforts to be completely explained. Lifetimes for most of the states under study were also measured, taking advantage of the use of a thick target.
Conclusions
The increase of the experimental resolution in g factors will be pivotal in the forthcoming years to compare with the results of recent theoretical efforts that try to explain the nuclear structure of stable and radioactive nuclei. The use of Coulomb excitation reactions, near the Coulomb barrier, allows the use of the α–transfer channel as an alternative to the low–yield production of some nuclear species. A better understanding of the α–transfer population mechanism could improve the quality of the results, giving information of the most desirable position in which to place the particle and the γ–ray detectors to obtain the best possible angular resolution and precession effect. A further theoretical study, and reevaluation, of the BTF parametrization is needed to improve the precision of future experiments, and to extend the validity of the parametrization to regions heavier than Pb and lighter than O.
The main challenge for future uses of the TF technique with radioactive beams is the presence of decaying radioactivity sub–products around the target. In this case, a modification of the experimental setup in Fig. 3 is needed to minimize the radioactive build up in the target. The modifications depend on the half–life (T1/2) of the nuclei; for lifetimes of the order of days or hours a thin cooper layer in the target (Fig. 3), which does not fully stop the beam, is used to accumulate the radioactive beam in a moving tape [18] between the target and the particle detector, or in a distant beam dump [19]. For longer T1/2 it is possible to consider the beam as stable, as has been recently shown in Ref. [20].
Acknowledgments
The author would like to thank to N. Benczer–Koller, G. Kumbartzki, Y. Y. Sharon, L. Zamick, and L.F. Cristancho for their comments to improve the manuscript.
References
[1] D. A. Torres, G. J. Kumbartzki, Y. Y. Sharon, L. Zamick, B. Manning, N. Benczer–Koller, G. Gürdal, K.–H. Speidel, M. Hjorth–Jensen, P. Maier–Komor, S. J. Q. Robinson, T. Ahn, V. Anagnostatou, M. Elvers, P. Goddard, A. Heinz, G. Ilie, D. Radeck, D. Savran, and V. Werner, Phys. Rev. C 84, 044327 (2011).
[2] D. A. Torres, G. J. Kumbartzki, Y. Y. Sharon, L. Zamick, B. Manning, N. Benczer–Koller, K.–H. Speidel, T. Ahn, V. Anagnostatou, M. Elvers, P. Goddard, A. Heinz, G. Ilie, D. Radeck, D. Savran, V. Werner, G. Gürdal, M. J. Taylor, P. Maier–Komor, M. Hjorth–Jensen, and S. J. Q. Robinson, Phys. Rev. C (In press).
[3] G. J. Kumbartzki, K.–H. Speidel, N. Benczer–Koller, D. A. Torres, Y. Y. Sharon, L. Zamick, S. J. Q. Robinson, P. Maier–Komor, T. Ahn, V. Anagnostatou, C. Bernards, M. Elvers, P. Goddard, A. Heinz, G. Ilie, D. Radeck, D. Savran, V. Werner, and E. Williams, Phys. Rev. C (To be published).
[4] A. E. Stuchbery, J. Phys.: Conf. Ser. (To be published).
[5] S. K. Chamoli, A. E. Stuchbery, S. Frauendorf, J. Sun, Y. Gu, R. F. Leslie, P. T. Moore, A. Wakhle, M. C. East, T. Kibédi, and A. N. Wilson, Phys. Rev. C 83, 054318 (2011).
[6] N. Benczer–Koller and G. J. Kumbartzki, J. Phys. G: Nucl. Part. Phys. 34, R321 (2007).
[7] R. R. Borchers, B. Herskind, J. D. Bronson, L. Grodzins, R. Kalish, and D. E. Murnick, Phys. Rev. Lett. 20, 424 (1968).
[8] N. K. B. Shu, D. Melnik, J. M. Brennan, W. Semmler, and N. Benczer–Koller, Phys. Rev. C 21, 1828 (1980).
[9] K.–H. Speidel, N. Benczer–Koller, G. Kumbartzki, C. Barton, A. Gelberg, J. Holden, G. Jakob, N. Matt, R. H. Mayer, M. Satteson, R. Tanczyn, and L. Weissman, Phys. Rev. C 57, 2181 (1998).
[10] T. J. Mertzimekis, N. Benczer–Koller, J. Holden, G. Jakob, G. Kumbartzki, K.–H. Speidel, R. Ernst, A. Macchiavelli, M. McMahan, L. Phair, P. Maier–Komor, A. Pakou, S. Vincent, and W. Korten, Phys. Rev. C 64, 024314 (2001).
[11] D. Ballon, Y. Niv, S. Vajda, N. Benczer–Koller, L. Zamick, and G. A. Leander, Phys. Rev. C 33, 1461 (1986).
[12] A. E. Stuchbery, I. Morrison, L. D. Wood, R. A. Bark, H. Yamada, and H. H. Bolotin, Nucl. Phys. A 435, 635 (1985).
[13] P. Maier–Komor, K. Speidel, and A. Stolarz, Nucl. Instrum. Methods Phys. Res. A 334, 191 (1993).
[14] P. Mater–Komor, Nucl. Instrum. Methods Phys. Res. A 282, 133 (1989).
[15] M. Saxena, S. Mandal, S. A. S., S. Abhilash, and D. Kabiraj, in proc: Proceeding of the DAE Symp.on Nucl.Phys. (2010) pp. 55–56.
[16] G. Gürdal, G. J. Kumbartzki, N. Benczer–Koller, Y. Y. Sharon, L. Zamick, S. J. Q. Robinson, T. Ahn, R. Casperson, A. Heinz, G. Ilie, J. Qian, V. Werner, E. Williams, R. Winkler, and D. McCarthey, Phys. Rev. C 82, 064301 (2010).
[17] P. Halse, J. Phys. G: Nucl. Part. Phys. 19, 1859 (1993).
[18] G. Kumbartzki, J. Cooper, N. Benczer–Koller, K. Hiles, T. Mertzimekis, M. Taylor, K.–H. Speidel, P. Maier–Komor, L. Bernstein, M. McMahan, L. Phair, J. Powell, and D.Wutte, Phys. Lett. B 591, 213 (2004).
[19] N. Benczer–Koller, G. Kumbartzki, G. Gürdal, C. Gross, A. Stuchbery, B. Krieger, R. Hatarik, P. O'Malley, S. Pain, L. Segen, C. Baktash, J. Beene, D. Radford, C. Yu, N. Stone, J. Stone, C. Bingham, M. Danchev, R. Grzywacz, and C. Mazzocchi, Phys. Lett. B 664, 241 (2008).
[20] G. J. Kumbartzki, N. Benczer–Koller, D. A. Torres, B. Manning, P. D. O'Malley, Y. Y. Sharon, L. Zamick, C. J. Gross, D. C. Radford, S. J. Q. Robinson, J. M. Allmond, A. E. Stuchbery, K.–H. Speidel, N. J. Stone, and C. R. Bingham, (In preparation).