PROPIEDADES ELECTRÓNICAS DE SISTEMAS TIPO PANAL DE ABEJAS EN DOS DIMENSIONES. UN ESTUDIO AB INITIO
ELECTRONIC PROPERTIES OF DIATOMIC TWO-DIMENSIONAL HONEYCOMB SYSTEMS. AN AB INITIO STUDY
Angela M. Rojas-Cuervo, Karen M. Fonseca-Romero, Rafael
R. Rey-González
Departamento de Física, Facultad de Ciencias, Universidad Nacional de Colombia - Sede
Bogotá, Carrera 30 Calle 45-03, CP 111321, Bogotá, Colombia.
(Recibido: Marzo/2015. Aceptado: Junio/2015)
Resumen
Las novedosas propiedades del grafeno han motivado la búsqueda de materiales que presenten caracteristicas similares. En el presente artículo se estudian la estabilidad química y la estructura de bandas de monocapas
hexagonales de GaAs y GaN, usando un formalismo de
primeros principios. Los resultados obtenidos mediante el código SIESTA, como implementación de la Teotría del
Funcional de la Densidad, muestran que el GaAs (GaN)
es un semiconductor con una brecha de energía prohibida indirecta (directa).
Palabras clave: Monocapas hexagonales, Propiedades electrónicas, DFT, DOS.
Abstract
The novel properties of graphene have motivated the search for materials with similar characteristics. In this work, we study the chemical stability and the band structures of GaAs and GaN hexagonal monolayers, using a first principles formalism. Results obtained with SIESTA code, as a DFT implementation, show GaAs (GaN) is an indirect (a direct) bandgap semiconductor.
Keywords: Hexagonal monolayers, Electronic properties, DFT, DOS.
1. Introducción
Actualmente, el auge de la nanotecnología como ciencia multidisciplinar se debe a la construcción y caracterización de una amplia variedad de materiales de baja dimensionalidad, tanto orgánicos como inorgánicos o mixtos [1]. En la investigación de estas nanoestructuras se utilizan técnicas de análisis en microscopía y métodos de simulación molecular, útiles no solo en el ámbito puramente académico [2], sino también en el campo de la investigación industrial [3].
Uno de los resultados recientes más importantes ha sido el aislamiento del grafeno mediante exfoliación mecánica [4]. Esta monocapa de átomos de carbono dispuestos en forma hexagonal, da cuenta de un material de estructura bidimensional cuya existencia se creía imposible debido a la inestabilidad termodinámica demostrada teóricamente por R. Peierls [5] y L. Landau [6].
El grafeno, que se ha investigado teórica y experimentalmente [4, 7, 8], tiene una relación de dispersión sin brecha de energía prohibida.
Una de las caracteríticas novedosas del grafeno es la linealidad de las bandas de conducción y de valencia alrededor del nivel de Fermi, que se encuentra en el punto K de la red recíproca. En esta zonas, conocidas como Conos de Dirac, los electrones y huecos se comportan como cuasipartículas sin masa que se mueven con una rapidez, independiente de su vector de onda, del orden de 106 m/s.
Teniendo en cuenta el importante descubrimiento del grafeno, nos cuestionamos si existen otros materiales bidimensionales estables que presenten una relación de dispersión electrónica lineal. La respuesta a esta pregunta ha motivado el desarrollo del presente trabajo, que explora las propiedades estructurales y electrónicas de monocapas hexagonales (h-GaAs, h-GaN) de un par de materiales que a través de los años han tenido una gran diversidad de aplicaciones tecnológicas: el GaN (Nitruro de galio) y el GaAs (Arsenuro de galio).
En la investigación de estos sistemas se utiliza el formalismo de primeros principios (ab initio) en su formulación DFT (Density Funcional Theory), implementado en el código SIESTA (Spanish Initiative for Electronic Simulations with Thousands of Atoms) [9]. En la siguiente sección se resentan algunos detalles computacionales relacionados con el método; luego (sección 3) se reportan los principales resultados y finalmente, las conclusiones
del trabajo (sección 4).
2. Detalles computacionales
En el estudio de las propiedades estructurales y electrónicas de las monocapas h-GaAs y h-GaN, se utiliza el código SIESTA. El cual es útil para realizar cálculos de estructura electrónica y simulaciones de dinámica molecular sin necesidad de ajuste a ningún dato experimental, empleando algoritmos eficientes con un costo computacional intermedio. El tiempo de cálculo escala linealmente con el número de átomos del sistema. En el cálculo de la energía de intercambio y correlación se utiliza la aproximación de gradiente generalizado (GGA) con el funcional Perdew-Burke-Ernzerhof (PBE)[10]. Los electrones de valencia se describen mediante orbitales atómicos numéricos localizados con una base de doble ![]() más polarización (DZP); los electrones profundos se tratan implícitamente usando pseudopotenciales que conservan la norma [11, 12] y radios de corte
más polarización (DZP); los electrones profundos se tratan implícitamente usando pseudopotenciales que conservan la norma [11, 12] y radios de corte ![]() optimizados [12, 13].
optimizados [12, 13].
El análisis de la estabilidad química de las estructuras se realiza mediante un proceso de relajación, en el que cada átomo de la celda unitaria se mueve paso a paso, minimizando la fuerza entre ellos.
3. Resultados
3.1. Parámetros de red
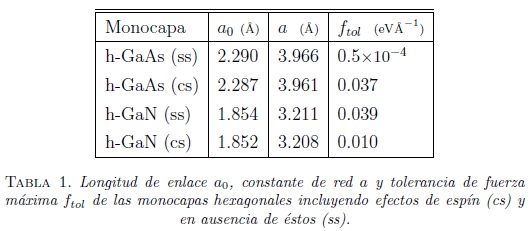
El proceso de relajación permite minimizar la energía y encontrar la configuración más estable. Se considera que una estructura química es estable cuando en el proceso de relajación la fuerza de tolerancia máxima es menor a ![]() por celda [9]. Posteriormente, se calculan la longitud de enlace a0 y la constante de red a. En este caso, los valores de a cambian apreciablemente al incluir los efectos de espín, como se puede observar en la tabla 1.
por celda [9]. Posteriormente, se calculan la longitud de enlace a0 y la constante de red a. En este caso, los valores de a cambian apreciablemente al incluir los efectos de espín, como se puede observar en la tabla 1.
En contra posición en sistemas hexagonales monoatómicos como el grafeno, el h-Si o el h-Ge esta dependencia no es observada [14].
Esto revela que los materiales heteropolares son más sensibles a los efectos debidos al espín, como el acoplamiento espín-orbita por ejemplo.
A la fecha y hasta nuestro conocimiento no existen reportes
experimentales de las constantes de red del h-GaAs y h-GaN. Con el fin de validar el presente procedimiento se calcula el parámetro de red para el silicene (h-Si) y se compara con el reportado en los resultados experimentales encontrados en la literatura. Se observa que este difiere dependiendo del sustrato usado en su crecimiento, sobre Ag(110) es de 3.88 ![]() [15], usando Ag(111) el valor es de a =
[15], usando Ag(111) el valor es de a =
3.3 ![]() [16] y a = 3.65
[16] y a = 3.65 ![]() para (0001)-ZrB2[17]. Al comparar estos resultados con los nuestros encontramos diferencias de 0.46 %,
14.55% y 5.49% respectivamente.
para (0001)-ZrB2[17]. Al comparar estos resultados con los nuestros encontramos diferencias de 0.46 %,
14.55% y 5.49% respectivamente.
De otra parte, existe controversia sobre la estabilidad química del h-GaN. Suzuki et al [18] reportan la no existencia de este sistema,
mientras Sahim et al [19] reportan un parámetro de red de 3.2![]() .
.
Ambos autores usan implementaciones DFT en un esquema menos preciso como es la Aproximación de Densidad Local (siglas en inglés: LDA). Nuestros resultados muestran la estabilidad química del h-GaN con un parámetro de red alrededor de 3.21 ![]() . En un trabajo previo de Rojas-Cuervo et al, [20] se muestra que el h-GaN es estable aún usando un formalismo DFT-LDA.
. En un trabajo previo de Rojas-Cuervo et al, [20] se muestra que el h-GaN es estable aún usando un formalismo DFT-LDA.
3.2. Relaciones de dispersión y densidades de estados.
El GaAs y el GaN tienen una estructura tridimensional tipo
zinc-blenda con brechas de energía prohibida directas de 1.42 eV [21{23] y 3.5 eV [24], respectivamente, útiles para la construcción
de dispositivos optoelectrónicos.
En forma bidimensional, i. e., como hojas hexagonales, preservan su comportamiento semiconductor, pero presentan efectos que modican su uso en la industria electrónica. La mayor variación la presenta el h-GaAs. Su gap es indirecto, mientras el h-GaN presenta un comportamiento de gap directo.
En las figuras 1 y 2 se muestran
El h-GaAs tiene el máximo de la banda de valencia en el punto K y el mínimo de la banda de conducción en el punto (ver Fig. 1).
Por su parte, el h-GaN exhibe un comportamiento semiconductor de gap directo, en el punto ![]() , como se puede apreciar en la Fig. 2.
, como se puede apreciar en la Fig. 2.



Los valores obtenidos para la brecha de energía incluyendo los efectos de espín (cs) o ignorándolos (ss) se pueden apreciar en la tabla 2. El valor de la brecha de energía depende de incluir el espín, o no. En esta tabla también se han incluido algunos valores reportados previamente. Nuestros valores para la brecha de energía difieren de los reportados previamente desde un mínimo 0,06 eV (ss) hasta un máximo de 0;18 eV (cs) en el caso del h-GaN. Para el h-GaAs estas diferencias van desde 0;56 eV hasta 1;16 eV. Las discrepancias encontradas para el h-GaN indican que este material monocapa debe ser analizado con un mayor cuidado, optimizando los valores críticos como el radio de corte, el número de los orbitales atómicos y la posible inclusión de pseudopotenciales con semicore para orbitales tipo d, entre otros.
Conclusiones
El esquema de optimización de los pseudopotenciales, en particular del radio de corte y de la configuración electrónica de cada uno de los átomos, permite obtener una buena concordancia de los resultados aquí reportados con valores experimentales.
h-GaAs y el h-GaN presentan estabilidad química, y conservan el carácter semiconductor de su fase tridimensional. Los gaps calculados de las monocapas hexagonales son menores que los de las respectivas estructuras tridimensionales. El h-GaAs presenta un mayor cambio, pues pasa de material con brecha directa (3D) a semiconductor de gap indirecto. Estas características pueden posibilitar una nueva forma de hacer ingeniería de band-gaps.
5. Agradecimientos
Los autores desean agradecer el apoyo financiero de la Division de Investigación Sede Bogotá, Universidad Nacional de Colombia, a través del proyecto 12584. A. M. Rojas-Cuervo agradece el soporte financiero de Colciencias, Colombia.
Referencias
[1] C. Poole and F. Owens, Introducción a la Nanotecnología (Reverté, 2003).
[2] "The code siesta is used in research centers as: Nersc, cesga, nnin among others." (2014).
[3] "In the industry field, motorola in 1999 used code siesta in the strontium titanium growth on silicon." (1999).
[4] K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, and A. A. Firsov, Science 306, 666 (2004).
[5] R. Peierls, Annales de I. H. P. 5, pp. 177 (1935).
[6] L. D. Landau, Phys. Z. Sowjetunion 11, 19 (1937).
[7] K. S. N. nd A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos, and A. A. Firsov, Nature 438, 197 (2005).
[8] A. K. Geim, K. S. Novoselov, and A. K. Geim, Nature Materials 6, 183 (2007).
[9] J. M. Soler, E. Artancho, J. D. Gale, A. García, J. Junquera, P. Ordejón, and D. Sánchez, J. Phys. Condens. Matter 14, 2745 (2002).
[10] J. P. Perdew, K. Burke, and M. Ernzerhof, Phy. Rev. Lett. 77 (1996), 10.1103/PhysRevLett.77.3865.
[11] N. Troullier and J. L. Martins, Phys. Rev. B 43 (1991), 10.1103/PhysRevB.43.1993.
[12] C. P. P. Barrera, Cálculo de las constantes de fuerza entre bases nitrogenadas del ADN aplicando el método SIESTA, Master's thesis, Universidad Nacional de Colombia (2010).
[13] C. A. Pabón-Espejo, Cálculo de la energía de enlace de las bases nitrogenadas Guanina-Citosina y Adenina-Timina, Master's thesis, Universidad Nacional de Colombia (2006).
[14] A. M. Rojas-Cuervo, K. Fonseca-Romero, and R. Rey-Gonzáles, Eur. Phys. J. B 87 (2014), 10.1140/epjb/e2014-40894-9.
[15] P. D. Padova, C. Quaresima, C. Ottaviani, P. M. Sheverdyaeva, P. Moras, C. Carbone, D. Topwal, B. Olivieri, A. Kara, H. Oughaddou, B. Aufray, and G. L. Lay, Appl. Phys. Lett. 96 (2010).
[16] B. Lalmi, H. Oughaddou, H. Enriquez, A. Kara, S. Vizzini, B. Ealet, and B. Aufray, Appl. Phy. Lett 97 (2010), 10.1063/1.3524215.
[17] A. Fleurence, R. Friedlein, T. Ozaki, H. Kawai, Y. Wang, and Y. Yamada-Takamura, Phys. Rev. Lett 108, 245501 (2012).
[18] T. Suzuki and Y. Yokomizo, Physica E Low Dimens. Syst. Nanostruct 42, 2820 (2010).
[19] H. Sahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger, and S. Ciraci, Phys. Rev. B 80,