
ESTUDIO DE LOS MODOS CONFINADOS EN UN CRISTAL FOTÓNICO UNIDIMENSIONAL PARA DIFERENTES LONGITUDES DEL DEFECTO AÑADIDO
STUDY OF CONFINED MODES IN AN UNIDIMENSIONAL PHOTONIC CRYSTAL FOR DIFFERENT DEFECT'S LENGTHS
Daniel G. Suárez-Forero, Luisa F. Ramírez
Grupo de óptica e Información Cuántica, Departamento de Física, Universidad Nacional de Colombia.
(Recibido: Abril/2015. Aceptado: Junio/2015)
Resumen
Con el fin de estudiar los efectos que tiene la variación de longitud de un defecto en un cristal fotónico unidimensional con condición λ =4, se hizo uso del método de expansión en ondas planas. Al aumentar dicha longitud desde 0 hasta λ, se encontró que la energía del modo confinado disminuye hasta desvanecerse en la banda dieléctrica, mientras que un nuevo modo comienza a desprenderse de la banda aérea. De igual forma, para longitudes mayores a λ, se observó una disminución de las energías correspondientes a estados excitados del sistema, lo que genera la aparición de múltiples modos confinados. Finalmente, se estudiaron la amplitud y la ubicación del gap, permitiendo concluir que estos parámetros no se ven alterados por el cambio en la longitud del defecto añadido.
Palabras clave: Cristal fotónico, modo confinado, band-gap
Abstract
With the aim of study the effects of a variation in the length of an unidimensional photonic cristal's defect with λ=4 condition, it was used the plane wave expansion method. When this length is increased from 0 to λ, it was found that the energy of the confined mode decreases until it vanishes in the dielectric band, while a new mode rises from the air band. In the same way, for a length larger than λ, it was observed a decrease on the energies corresponding to diferent excited states of the system, generating the appeareance of multiple confined modes. Finally, it was studied amplitude and gap's location, concluding that this parameters do not change with the defect's length variation.
Keywords: Photonic crystals, confined mode, band-gap
1. Introducción
Los cristales fotónicos son buenos candidatos para el desarrollo de dispositivos optoelectrónicos debido al gran control sobre la propagación de la luz que brinda la periodicidad en su función dieléctrica [1]. La presencia de modos prohibidos en su diagrama de dispersión ha permitido el desarrollo de aplicaciones como el confinamiento de luz [2, 3] (de gran interés para la materia condensada y la óptica cuántica [4]) y la construcción de guías de onda [5, 6] (con factores de calidad mayores que los de la fibra óptica).
En el presente trabajo se usa el método de expansión en ondas planas [7] con el fin de estudiar el cambio en las propiedades de un cristal fotónico unidimensional bajo variaciones de la longitud del defecto ubicado en el centro del mismo. Teniendo en cuenta que el método hace uso del teorema de Bloch [8], se asume que las condiciones de frontera del sistema son periódicas, por tanto, para obtener el diagrama de bandas se hace una expansión de la función dieléctrica en series de fourier, con el fin de solucionar de forma numérica la ecuación maestra del sistema proveniente de las ecuaciones de maxwell para medios [9].
1.1. Expansión en ondas planas de la función 1 / ε
Debido a que los materiales con los que está construido el cristal son considerados homogéneos e isotrópicos [10], es posible definir una velocidad de grupo y relacionarla con la permitividad y la permeabilidad del sistema por medio de la expresión v = 1 / √2 ε μ. Así mismo, se tiene que la razón entre la velocidad de propagación de la onda en el vacío y en un medio, viene definida por n = c/v. Con estas dos ecuaciones, es posible construir la función permitividad en términos del índice de refracción. ésto con el ánimo de solucionar la ecuación de autovalores derivada de la ecuación maestra para el campo magnético [12].

Fígura 1. Esquema de la super-celda
Según la figura 1, los coeficientes de la expansión de 1=ε en ondas planas están dados por:
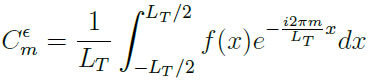
![]()
Donde LT es la longiud total de la super celda y f(n) toma el valor de ![]() dependiendo del intervalo de integración.
dependiendo del intervalo de integración.
2. Análisis y resultados
Para los cristales λ=4, como el estudiado en este caso, se tiene que el confinamiento es óptimo para un defecto de longitud λ, pues bajo esta condición el modo confinado se ubica justo en la mitad del gap fotónico, maximizando el factor de calidad de la cavidad [1, 13] como lo muestra la figura 2.

FIGURA 2. Diagrama de dispersión de un cristal fotónico unidimensional λ=4 con defecto de longitud λ.
Los parámetros usados fueron: n1=1, n2=3, L1=1/(4n1), L2=1/(4n2). El defecto tiene índice de refracción n2 y longitud 1/n2.
Al variar la longitud del defecto, se pudo observar que el gap fotónico permanece inalterado, mientras que el modo confinado sí cambia su posición.
La figura 3 muestra la posición del modo confinado para diferentes longitudes del defecto.
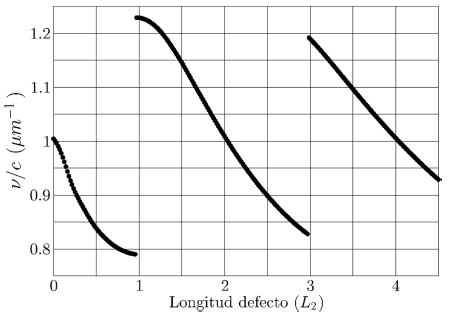
Figura 3. Energía del modo confinado como función de la longitud del defecto en un cristal unidimensional (la unidad base de longitud se toma como L2).
Los parámetros usados fueron: n1=1, n2=3, L1=1=(41), L2=1/(4n2). El defecto tiene índice de refracción n2.

Figura 4. Panel izquierdo: Diagrama de bandas para un cristal fotónico cuyo defecto tiene longitud 6,7L2 e índice de refraccion n2. Panel derecho: Perfiles de campo eléctrico de los modos dentro del band-gap para el mismo cristal. Nótese que ambos son confinados. Los parámetros usados son:
n1=1, n2=3, L1=1/(4n1), L2=1/(4n2).
Se observa que a medida que se aumenta la longitud de la cavidad, la energía del modo confinado disminuye. Sin embargo, para ciertos valores de longitud, existe una discontinuidad, debido a que tras la disminución de la energía del modo confinado, este entra a hacer parte de la banda dieléctrica, mientras que de la banda aérea se desprende un nuevo modo que toma su lugar. Dicho comportamiento se mantiene hasta que la longitud toma el valor de λ, ya que a partir de este momento comienza a haber más de un modo confinado dentro del band-gap, como lo muestra la figura 4. Los perfiles de campo eléctrico, permiten corroborar que ambos modos son confinados. Esto es debido a que la energía del modo de la cavidad es inversamente proporcional a su longitud. Por lo tanto, al aumentarla, la frecuencia de los modos excitados disminuye lo suficiente como para entrar en el primer gap fotónico. Esto implica que para longitudes mucho mayores a L2, la cantidad de modos confinados dentro del primer gap aumenta considerablemente. La figura 5 muestra el diagrama de bandas para el caso en que la longitud del defecto es 12.5L2. Como se puede observar, existen 4 modos dentro del gap energético cuya velocidad de grupo es cero; condición que permite confirmar que éstos son confinados. El análisis permite concluir que se pueden tener tantos modos confinados dentro de un mismo gap como se desee, siempre y cuando la longitud del defecto sea la adecuada.
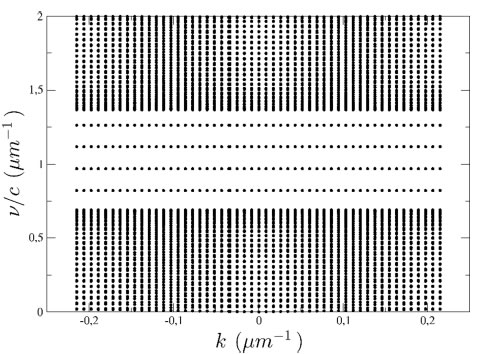
Figura 5. Diagrama de bandas para cristal fotónico con defecto de longitud 12,5L2. El diagrama de bandas muestra cuatro modos confinados. Entre mayor sea la longitud del defecto, más modos confinados tendrá el primer gap. Los parámetros usados son: n1=1, n2=3, L1=1/(4n1), L2=1/(4n2).
Conclusiones
Ante una variación de la longitud del defecto en un cristal fotónico unidimensional, la posición y el ancho del gap fotónico permanecen inalterados; es el modo confinado el que se ve afectado por dicha variación: su energía disminuye a medida que el defecto se elonga. Vale la pena también remarcar que después de la longitud λ, el band-gap empieza a aceptar múltiples modos confinados debido a la disminución de energía de los estados excitados.
Agradecimientos
Los autores agradecen a Juan Pablo Vasco cuyo curso sobre cristales fotónicos motivó y permitió la escritura del presente artículo. De igual forma agradecen a Herbert Vinck Posada, Profesor del departamento de física de la Universidad Nacional de Colombia asociado al Grupo de Óptica e Información Cuántica, cuya asesoría acádemica y discusiones han sido de enorme valor durante la escritura de este texto y a lo largo de toda la formación profesional de los autores. Este trabajo he recibido financiamiento parcial de COLCIENCIAS proveniente del proyecto "Exploración y modelación de la iridiscencia en especies colombianas", código HERMES 17432 y código en COLCIENCIAS 110156933525, a cargo del Profesor Herbert Vinck Posada.
Referencias
[1] J. D. Joannopoulos, S. G. Johnson, J. N. Winn, and R. D. Meade, Photonic crystals: molding the ow of light, 2nd ed. (Princeton University Press, 2007).
[2] K. Srinivasan, P. E. Barclay, O. Painter, J. Chen, A. Y. Cho, and C. Gmachl, Applied Physics Letters 83, 1915 (2003).
[3] K. J. Vahala, Nature 424 (2003).
[4] Reithmaier J. P., Sek G., Loffer A., Hofmann C., Kuhn
S., Reitzenstein S., Keldysh L. V., Kulakovskii V. D.,
Reinecke T. L., and Forchel A., Nature 432, 197 (2004),
10.1038/nature02969.
[5] M. Notomi, K. Yamada, A. Shinya, J. Takahashi, C. Takahashi, and I. Yokohama, \Photonic crystal waveguide," (2003), uS Patent 6,643,439.
[6] M. Tokushima, H. Kosaka, A. Tomita, and H. Yamada, Applied physics letters 76, 952 (2000).
[7] A. Danner, \An introduction to the plane wave expansion method for calculating photonic crystal band diagrams," (2002).
[8] C. Kittel, Introduction to solid state physics, eight ed. (John Wiley and Sons, Inc).
[9] J. D. Jackson, Classical electrodynamics, 3rd ed. (John Wiley and Sons, Inc, 1999).
[10] C. J. Knight, Nature 424 (2003).
[11] A. Bard and L. Faulkner, Electrochemical Methods: Fundamentals and Applications (Wiley, 2000).
[12] J.-Y. Veuillen, J.-M. Gomez-Rodriguez, and R. C. Cinti (AVS, 1996) pp. 1010{1014.
[13] E. Garmire, Applied Optics 42 (2003).