
RENDIMIENTO TERMOELÉCTRICO EN COMPÓSITOS DE 
TERMOELECTRIC PERFORMANCE OF  COMPOSITES
COMPOSITES
José D. Támara, Julio E. Rodríguez
Departamento de Física, Universidad Nacional de Colombia, Sede Bogotá, Colombia.
Jose D. Tómara: jdtamaraj@unal.edu.co
Julio E. Rodríguez: jerodriguezl@unal.edu.co
(Recibido: Noviembre/2015. Aceptado: Diciembre/2015)
Resumen
Utilizando el método de reacción de estado sólido se prepararon compósitos de  , donde el contenido de plata tomo valores en proporciones de masa entre 0% y 10%. Sus propiedades de transporte se estudiaron en función de la temperatura a partir de mediciones de resistividad eléctrica p(T) y coeficiente Seebeck S(T). La magnitud de la resistividad eléctrica decrece con el contenido de plata presente, hasta valores próximos a 3 mΩ - cm. El coeficiente Seebeck es positivo en todo el rango de temperatura estudiado sugiriendo una conducción eléctrica dada por portadores de carga positivos. El rendimiento termoeléctrico se evaluó a partir del cálculo del factor de potencia PF, el cual se incrementa con el nivel de plata adicionada alcanzando valores máximos cercanos a 9.5 µW/K2cm. El comportamiento mostrado por las propiedades de transporte permiten proponer estos compósitos como potenciales materiales con aplicaciones termoeléctricas.
, donde el contenido de plata tomo valores en proporciones de masa entre 0% y 10%. Sus propiedades de transporte se estudiaron en función de la temperatura a partir de mediciones de resistividad eléctrica p(T) y coeficiente Seebeck S(T). La magnitud de la resistividad eléctrica decrece con el contenido de plata presente, hasta valores próximos a 3 mΩ - cm. El coeficiente Seebeck es positivo en todo el rango de temperatura estudiado sugiriendo una conducción eléctrica dada por portadores de carga positivos. El rendimiento termoeléctrico se evaluó a partir del cálculo del factor de potencia PF, el cual se incrementa con el nivel de plata adicionada alcanzando valores máximos cercanos a 9.5 µW/K2cm. El comportamiento mostrado por las propiedades de transporte permiten proponer estos compósitos como potenciales materiales con aplicaciones termoeléctricas.
Palabras clave: Rendimiento termoeléctrico, Compósitos de  , Propiedades de transporte.
, Propiedades de transporte.
Abstract
By using the solid state reaction method composites of  were growth, the silver weight ratios take values between 0% and 10%. Their transport properties were studied from electrical resistivity p(T) and Seebeck coefficient S(T) measurements as function of temperature. The magnitude of the electrical resistivity decreases with the Ag content present in the composites. The Seebeck coefficient is positive throughout the studied temperature range suggesting a conduction given by positive charge carriers. Thermoelectric performance was assessed through the thermoelectric power factor, PF, which increases with the added Ag level. This parameter reaches maximum values around 9.5 µW/K2cm. . The observed behaviour in the transport properties become these ceramic composites promising thermoelectric materials.
were growth, the silver weight ratios take values between 0% and 10%. Their transport properties were studied from electrical resistivity p(T) and Seebeck coefficient S(T) measurements as function of temperature. The magnitude of the electrical resistivity decreases with the Ag content present in the composites. The Seebeck coefficient is positive throughout the studied temperature range suggesting a conduction given by positive charge carriers. Thermoelectric performance was assessed through the thermoelectric power factor, PF, which increases with the added Ag level. This parameter reaches maximum values around 9.5 µW/K2cm. . The observed behaviour in the transport properties become these ceramic composites promising thermoelectric materials.
Keywords: Thermoelectric performance,  composites, Transport properties.
composites, Transport properties.
Introducción
El incremento del consumo de combustibles fósiles utilizados en la generación de energía eléctrica, unido al impacto ambiental derivado de la utilización de estas materias primas ha motivado la búsqueda de nuevas fuentes de energía que puedan mitigar su impacto ambiental. Dentro de las fuentes alternativas de energía limpia, los materiales termoeléctricos permiten la conversión directa de energía térmica en eléctrica y viceversa. Por lo tanto, es de gran interés la investigación encaminada hacia la búsqueda de nuevos materiales con propiedades termoeléctricas, los cuales darían lugar al diseño de dispositivos refrigeradores y generadores eléctricos de estado sólido más eficientes [1].
Actualmente
los mejores dispositivos refrigeradores utilizan materiales semiconductores
basados en aleaciones binarias de  , las cuales muestran una figura de mérito
con valores próximos a la unidad. Estos producen únicamente moderados niveles
de enfriamiento, resultando ineficientes si se les compara con los
refrigeradores convencionales. Como un resultado estos dispositivos se utilizan
principalmente en aplicaciones en las cuales la conveniencia y la confiabilidad
son más importantes que la economía.
, las cuales muestran una figura de mérito
con valores próximos a la unidad. Estos producen únicamente moderados niveles
de enfriamiento, resultando ineficientes si se les compara con los
refrigeradores convencionales. Como un resultado estos dispositivos se utilizan
principalmente en aplicaciones en las cuales la conveniencia y la confiabilidad
son más importantes que la economía.
La consecución de nuevos materiales termoeléctricos es una consecuencia del desarrollo de nuevas teorías provenientes de la física del estado sólido, las cuales permiten además de "diseñar "nuevos compuestos con estructuras cristalinas complejas contribuir al entendimiento y optimización de sus propiedades físicas.
Por otro lado, los óxidos cerámicos con propiedades termoeléctricas se caracterizan por mostrar gran estabilidad química, así como por su capacidad para trabajar en un amplio rango de temperatura[2, 3]. Sin embargo, se ha encontrado que sus propiedades de transporte se ven afectadas por factores como las distorsiones de la red cristalina, inhomogeneidades estructurales y redistribución química, por ello es necesario conocer y controlar estos parámetros a fin de optimizar sus propiedades de transporte [4, 5].
La
desventaja principal de las cerámicas como materiales termoeléctricos es su
elevada resistividad (comparada con los metales y semiconductores
convencionales), así que una disminución efectiva de esta es la clave para
incrementar el rendimiento termoeléctrico de estos compuestos. Las estrategias
utilizadas para la optimización de sus propiedades de transporte involucran la
sustitución parcial de sus elementos constituyentes a fin de alterar la
densidad de los portadores de carga y/o la adición de elementos conductores con
la finalidad de mejorar las propiedades eléctricas[6]. En
este sentido, aquí se muestran los resultados de la preparación de compasitos
de  para diferentes
niveles de plata adicionada y su caracterización mediante mediciones de
resistividad eléctrica y coeficiente Seebeck en función de la temperatura, con
la finalidad de evaluar su posible utilidad como material termoeléctrico.
para diferentes
niveles de plata adicionada y su caracterización mediante mediciones de
resistividad eléctrica y coeficiente Seebeck en función de la temperatura, con
la finalidad de evaluar su posible utilidad como material termoeléctrico.
Procedimiento Experimental
Mediante el
método de reacción de estado sólido se prepararon óxidos cerámicos con una
composición nominal de  . Esto se realizó a
partir de la mezcla de los compuestos
. Esto se realizó a
partir de la mezcla de los compuestos  (Merck 99,99%), los cuales se mezclaron
estequiométricamente utilizando un mortero de ágata y un molino de bolas
planetario. La mezcla se sometió a un proceso térmico a 9000C
durante 12 horas. El material resultante se molió y empastillo en frío bajo una
presión de 234MPa. Seguidamente se aplicó un segundo tratamiento térmico a 9000C
durante 48 horas en una atmósfera rica en oxígeno. Después de las etapas
expuestas se obtuvieron muestras cerámicas con la composición y estructura
esperada.
(Merck 99,99%), los cuales se mezclaron
estequiométricamente utilizando un mortero de ágata y un molino de bolas
planetario. La mezcla se sometió a un proceso térmico a 9000C
durante 12 horas. El material resultante se molió y empastillo en frío bajo una
presión de 234MPa. Seguidamente se aplicó un segundo tratamiento térmico a 9000C
durante 48 horas en una atmósfera rica en oxígeno. Después de las etapas
expuestas se obtuvieron muestras cerámicas con la composición y estructura
esperada.
Para la
obtención de los compósitos se adicionó nitrato de plata al compuesto cerámico
preparado previamente, en tal cantidad que aporte plata en las siguientes
proporciones de masa 1%, 3%, 5%, 8%, 10%. Para conseguir esto el material
cerámico de  y el nitrato de
plata se mezclaron homogéneamente y empastillaron en frío. Finalmente, las
muestras se trataron térmicamente a 9000C durante 10 horas.
El método diferencial y el método de cuatro sondas fueron utilizados en la
medición del coeficiente Seebeck y la resistividad eléctrica, respectivamente.
Adicionalmente, las propiedades estructurales y morfológicas se estudiaron a
través de análisis de difracción de rayos-X y microscopía electrónica de
barrido.
y el nitrato de
plata se mezclaron homogéneamente y empastillaron en frío. Finalmente, las
muestras se trataron térmicamente a 9000C durante 10 horas.
El método diferencial y el método de cuatro sondas fueron utilizados en la
medición del coeficiente Seebeck y la resistividad eléctrica, respectivamente.
Adicionalmente, las propiedades estructurales y morfológicas se estudiaron a
través de análisis de difracción de rayos-X y microscopía electrónica de
barrido.
Resultados
Los
patrones de difracción de rayos-X se obtuvieron utilizando un difracto metro x'pert
pro-panalytical, con una radiacion Cu Kα =
1.54056°A, la adquisición de datos se realizó en el rango de 2Θ entre 50 y 650, con un paso de 0.020. En la figura 1 se muestran los difractogramas típicos observados en las diferentes muestras
estudiadas. El refinamiento de la estructura cristalina se realizó utilizando
el softwere Powder Cell [7]. En todos los casos se
observa la presencia del compuesto cerámico  y en los compósitos con un nivel de plata
adicionada mayor al 3% se puede apreciar las reflexiones correspondientes a la
plata metálica. El compuesto cerámico presenta una estructura de carácter
ortorrombico, donde los parámetros de red y el volumen de la celda unitaria no
se alteran significativamente con el nivel de plata adicionada (Ver tabla 1). Esto hace evidente la no sustitución de los elementos
constitutivos del material cerámico por átomos de la plata adicionada.
y en los compósitos con un nivel de plata
adicionada mayor al 3% se puede apreciar las reflexiones correspondientes a la
plata metálica. El compuesto cerámico presenta una estructura de carácter
ortorrombico, donde los parámetros de red y el volumen de la celda unitaria no
se alteran significativamente con el nivel de plata adicionada (Ver tabla 1). Esto hace evidente la no sustitución de los elementos
constitutivos del material cerámico por átomos de la plata adicionada.
Las propiedades morfológicas de las muestras se estudiaron mediante microscopía electrónica de barrido (SEM), utilizando un detector de electrones retrodispersados (BSE). En la figura 2 se muestran las micrografás tápicas detectadas en los compósitos preparados con distintos porcentajes de plata adicionada. En general, se observa una matriz formada por el material cerámico y partículas de plata en el medio intergranular, cuyo tamaño se incrementa con el nivel de plata adicionada (ver recuadros en la figura 2), esto último es el resultado del proceso de aglomeración de las macropartículas de plata cuando la densidad de estas se incrementa, alcanzando valores superiores a 1μm en las muestras con elevadas concentraciones de plata. Este proceso de aglomeración da lugar a la perdida de homogeneidad de la distribución de la plata en las muestras, lo cual es un proceso no es deseado. La dinámica de la aglomeración de elementos conductores en la formación de compásitos con materiales cerámicos ha sido estudiada en trabajos previos con los mismos objetivos del presente trabajo [8-10].
La figura 3 muestra el comportamiento de la resistividad eléctrica en función de la temperatura para los diferentes compuestos preparados. En todos los casos la resistividad se incrementa con la temperatura mostrando un comportamiento de carácter metálico, mientras que la magnitud de p(T) decrece con el contenido de plata, desde aproximadamente 13 mΩ - cm hasta 3 m Ω - cm, esto se debe a que las partículas de plata contribuyen al mejoramiento del medio intergranular de la cobaltita, por lo tanto la dispersión entre granos se reduce, y como consecuencia la magnitud de la resistividad del compásito disminuye.
Por otra parte, el comportamiento del coeficiente Seebeck en función de la temperatura y el contenido de plata se presenta en la figura 4. Como se puede observar, el coeficiente Seebeck es positivo en todo el rango de temperatura considerado. Esto indica que la conducción eléctrica es debida a portadores de carga mayoritariamente positivos [11]. La magnitud de S(T) decrece con el nivel de plata adicionada, lo cual sugiere que las partículas de plata sirven como cortocircuitos para las diferencias de potencial generadas por el gradiente de temperatura, reduciendo, en esta forma, el coeficiente Seebeck del composite.
Propiedades termoeléctricas
Los materiales termoeléctricos pueden ser utilizados tanto en la refrigeración como en la generación de potencia, mediante dispositivos de estado sólido. En un refrigerador, por ejemplo, el calor es bombeado desde el extremo frío hacia el extremo caliente, la cantidad de calor que puede ser bombeada usando el efecto Peltier es justamente ST1, asá, se debe esperar contar con materiales con altos valores para el coeficiente Seebeck, S y bajos valores para la resistividad eléctrica, para asá minimizar las perdidas irreversibles de calor generadas por efecto Joule, I2R[12]. Finalmente, la conductividad térmica del material debe ser pequeña a fin de reducir el flujo natural de calor del extremo caliente al frío. Teniendo en cuenta estos factores, es posible demostrar que el parámetro que determina la eficiencia del dispositivo termoeléctrico depende de las propiedades de transporte del material. Por otra parte, el principio de funcionamiento de un generador termoeléctrico es similar al de una maquina térmica, la cual emplea los portadores de carga como portadores de energía térmica. La eficiencia de estos dispositivos es gobernada por la eficiencia de Carnot y por su figura de mérito adimensional del material, ZT. Entonces su eficiencia se define como:
donde Th y Tc son las temperaturas de los terminales caliente y frío,
respectivamente, 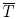 es el promedio
entre Th y Tc [12]. La figura de
mérito adimensional es una función de las propiedades de transporte y es
expresada como[13-15]:
es el promedio
entre Th y Tc [12]. La figura de
mérito adimensional es una función de las propiedades de transporte y es
expresada como[13-15]:
donde, ρ es la resistividad eléctrica, κ la conductividad térmica del material a una temperatura absoluta, T. Es importante notar que en un conductor o semiconductor, el calor es transportado tanto por portadores de carga como por fonones. Así, la conductividad térmica total tiene dos contribuciones: κ = κe + κf. Este hecho permite minimizar la contribución fononica mediante la generación de centros de dispersión de fonones, sin alterar en forma significativa las propiedades eléctricas del compuesto. Dando lugar a un cremento de la figura de merito.
El objetivo central de las investigaciones en materiales termoeléctricos lo constituye encontrar compuestos con altos valores para su figura de mérito. Esto se puede lograr mediante la reducción de la conductividad térmica y/o a través de la optimización de las propiedades de transporte, este último proceso debe conducir a un incremento del factor de potencia. Este parámetro de rendimiento es una función de la masa efectiva y la movilidad de los portadores de carga y es definido por la expresión:
Entonces, un buen material termoeléctrico se caracteriza por tener altos valores para su coeficiente Seebeck, lo cual implica la generación de grandes diferencias de potencial por pequeños gradientes térmicos y una baja resistividad eléctrica permite minimizar las perdidas por calentamiento Joule.
A partir de las mediciones de coeficiente Seebeck y resistividad eléctrica fue posible calcular el factor de potencia termoeléctrico de los compósitos en estudio, su comportamiento se observa en la figura 5. Este parámetro se incrementa con la adición de plata alcanzando valores máximos cercanos a 9.5 μW/K2cm, para el caso de la muestra con Ag = 5%, mostrando un incremento mayor al 200%, respecto de los compuestos sin plata adicionada. Este comportamiento es debido al decrecimiento de la resistividad eléctrica con la adición de plata en el compuesto, el cual es más significativo que la reducción del coeficiente Seebeck. Sin embargo, se espera que el factor de potencia muestre un valor óptimo dado por los valores mostrados por S (T ) y p(T ) con la adición de plata, pues este parámetro viene dado por la expresión PF = S2/ρ.
Se puede asumir que las partículas de plata tienen un doble papel dentro del compósito. Por una parte, mejora las conexiones eléctricas entre los granos de la cobaltita reduciendo, asó, la resistividad eléctrica y por otra parte, forma caminos de fácil conducción, los cuales sirven como cortocircuitos internos los que tienen un efecto degenerativo sobre el coeficiente Seebeck. En consecuencia, si las partículas de plata son mas pequeñas que los granos de la cobaltita y están bien distanciadas su efecto sobre el coeficiente Seebeck es despreciable, pero si por el contrario, estas están próximas o aglomeradas formando granos comparables con los del material cerámico, entonces los portadores de carga tenderán a circular a través de ellos dando origen a una reducción en el coeficiente Seebeck [16, 17].
Conclusiones
Mediante
el método de reacción de estado sólido es posible preparar compositos del tipo  . El estudio de
difracción de rayos-X no evidencio la penetración de los elementos conductores
a la estructura del material cerámico.
. El estudio de
difracción de rayos-X no evidencio la penetración de los elementos conductores
a la estructura del material cerámico.
La resistividad eléctrica disminuye por efecto de la adición de plata tomando valores mínimos próximos a 3 mΩ - cm. Mientras que el coeficiente Seebeck es positivo en todo el rango de temperatura estudiado, indicando una conducción dada por portadores de carga positivos.
El rendimiento termoeléctrico de los compósitos obtenidos se evaluó a través del cálculo del factor de potencia, el cual se incrementa con el nivel de plata adicionado alcanzando valores máximos cercanos a 9.5 μW/Κ2cm en el caso de la muestra con un 5 % de plata adicionada.
El comportamiento exhibido por las propiedades de transporte y el factor de potencia termoeléctrico muestran que la adición de elementos altamente conductores incrementan las propiedades termoeléctricas de estas cerámicas, sin embargo es necesario optimizar los tratamientos térmicos a fin de controlar el proceso de aglomeración de la plata.
Referencias
[1] J. E. Rodríguez, Momento 28, 3 (2004).
[2] J. E. Rodríguez, Rev. Acad. Colombiana de Ciencias 31, 545 (2007).
[3] I. Terasaki, Y. Sasago, and K. Uchinokura, Phys. Rev. B 56, R12685 (1997).
[4] S. Yamanaka, H. Kobayashi, and K. Kurosaki, Alloys Comp. 349, 321 (2003).
[5] S. Li, R. Funahashi, I. Matsubara, H. Yamada, K. Ueno, and S. Sodeoka, Ceram. Int. 27, 321 (2001).
[6] Y. Wang, Y. Sui, J. Cheng, X. Wang, and W. Su, J. Phys. D: Appl. Phys. 41, 045406 (2008).
[7] W. Kraus and G. Nolze, J. Appl. Cryst. 29, 301 (1996).
[8] T. Kimura, T. Yoshimoto, N. Iida, Y. Fujita, and T. Yamaguchi, J. Am. Ceram. Soc. 72, 85 (1989).
[9] S. Wang, Z. Bai, H. Wang, Q. Lu, J. Wang, and G. Fu, J. Alloys Compd. 554, 254 (2013).
[10] Y. Wang, Y. Sui, J. Cheng, X. Wang, and W. Su, J. Alloys Compd. 477, 817 (2009).
[11] A. C. Masset, C. Michel, A. Maignan, M. Hervieu, O. Toulemonde, F. Studer, B. Raveau, and J. Hejtmanek, Phys. Rev. B 62, 166 (2000).
[12] D. Rowe and C. Bhandari, Modern Thermoelectrics (Reston Publishing Company, 1983).
[13] D. Rowe, CRC Handbook of Thermoelectrics (CRC Press, 1995).
[14] G. Nolas, J. Sharp, and H. Goldsmid, Thermoelectrics, Basic Principles and New Materials Developments (Springer-Verlag, 2001).
[15] G. Mahan, B. Sales, and J. Sharp, Phys. Today 50, 42 (1997).
[16] M. Mikami, N. Ando, and R. Funahashi, J. Solid State Chem. 178, 2186 (2005).
[17] P. Xiang, Y. Kinemuchi, H. Kaga, and K. Watari, J. Alloys Compd. 454, 364 (2008).