
DYNAMICS AND ENTANGLEMENT OF A QUANTUM DOT-CAVITY SYSTEM COUPLED BY A NON-LINEAR OPTICAL INTERACTION
DINÁMICA Y ENTRELAZAMIENTO DE UN SISTEMA CAVIDAD-PUNTO CUÁNTICO ACOPLADO POR MEDIO DE UNA INTERACCIÓN ÓPTICA NO LINEAL
Edgar A. Gómez1, Santiago E. Arteaga1, Herbert Vinck-Posada2
1 Programa de Física, Universidad del Quindío, Armenia, Colombia.
2 Grupo de (Óptica e Información Cuántica, Departamento de Física, Universidad Nacional de Colombia, Bogotá, Colombia.
Edgar A. Gómez: eagomez@uniquindio.edu.co
(Recibido: Agosto/2016. Aceptado: Octubre/2016)
Abstract
We propose a simple theoretical model for a dissipative quantum dot-microcavity system interacting with a non-linear optical interaction. The Lindblad master equation formalism is considered to study the full dynamics for both weak and strong coupling regimes. The photoluminescence spectra of the system at the stationary limit is calculated in an exact form, and the effect due to non-linear optical interaction is explicitly evidenced. The entanglement of the system is calculated, and we found revivals and sudden death are evidenced. We also study the relationship between the light-matter and non-linear optical interaction terms by calculating the average photon number.
Keywords: Entanglement, quantum dot, microcavity, non-linear optical interaction.
Resumen
Se propone un modelo teórico sencillo para un sistema disipativo de punto cuántico-microcavidad que interactúan a través de una interacción óptica no lineal. El formalismo de la ecuación maestra en la forma de Lindblad es considerado para estudiar la dinámica del sistema en los regímenes de acoplamiento débil y fuerte, respectivamente. El espectro de fotoluminiscencia del sistema en el límite estacionario es calculado en forma exacta, y se muestra el efecto de la interacción óptica no lineal explícitamente sobre este. Se calcula el entrelazamiento del sistema, y se encuentra resurgimientos y muerte súbita del entrelazamiento. Adicionalmente, se estudia la relación entre los términos de interacción luz-materia (Jaynes-Cummings) e interacción óptica no lineal (medio Kerr) por medio del número medio de fotones.
Palabras clave: Entrelazamiento, punto cuántico, microcavidad, interacción óptica no lineal.
Introduction
Recently, nonlinear photonic crystals (PCs) and microcavities have attracted much attention due to their important applications, particularly due to the possibility to control the light propagation and the enhancement of various nonlinear optical phenomena. For example, the Second-Harmonic (SHG) and Third-Harmonic (THG) generation [1, 2] have wide applications as electro-optic modulators and optical switches [3]. Unusual effects like off-resonant dot-cavity interaction, photon blockade, generation of entangled photons and the Purcell enhancement have a number of applications in nano-photonics devices and quantum information processing [4]. The embedding the quantum dots in photonic band-gap structures offers a way of controlling spontaneous emission of single photons due to nonlinearities of light-matter coupling strength, and enabling cavity-quantum electrodynamics experiments [5]. For example, the bistability phenomenon can be observed as the result of the Kerr effect (due to the presence of other QDs in the cavity). It describes a self-interaction of a mode of radiation field in a cavity filled by X3-nonlinear medium. Moreover it is known to be responsible, in particular, for dispersive optical bistability and for amplitude squeezing [6], and has also been used to describe formation of Schrodinger-cat states [7]. In the present paper, we propose a simple theoretical model for describing a quantum dot-cavity (QD-Cavity) system coupled by a non-linear optical interaction (Kerr medium), and we investigate the effects on the dynamics of the system in both weak and strong coupling regimes, as well as on photoluminescence spectrum and the entanglement of the system. This paper is organized as follows: section 1 explains the theoretical background of our model, as well as the Lindblad master equation formalism for studying the QD-Cavity system. In addition, we discuss the theoretical tools for computing the photoluminescence spectrum and the quantification of entanglement. In section 2 the results are discussed. Finally, we conclude in section 2.4.
1 Theoretical Background
We are interested in study a quantum dot embedded in a micropillar cavity (QD-Cavity system) coupled by a confined mode of the electromagnetic field, that interacts with a non-linear optical interaction. This nonlinearity can be involved by considering an effective Kerr medium that incorporate two-photon absorption, it is a process where two photons are absorbed simultaneously, exciting e.g. a quantum dot to a higher-lying state, with the energy increase being equal to the sum of the photon energies. The QD-Cavity system is depicted in Fig. 1, and the non-linear system can be modelled, in the rotating wave approximation, by the following Hamiltonian
where 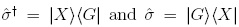 are the exciton operators, and ↠(â) is the creation (annihilation) operators for photons. ωα and ω are the exciton and photon energy, respectively (we have set h =1). The light-matter interaction is modeled by the well-known Jaynes-Cummings interaction g (JC), and the non linear optical interaction by the k parameter. We also define the detuning between field and cavity frequency as Δ = ω - ωα.
are the exciton operators, and ↠(â) is the creation (annihilation) operators for photons. ωα and ω are the exciton and photon energy, respectively (we have set h =1). The light-matter interaction is modeled by the well-known Jaynes-Cummings interaction g (JC), and the non linear optical interaction by the k parameter. We also define the detuning between field and cavity frequency as Δ = ω - ωα.
The Hamiltonian given by the Eq. (1) can be diagonalized when it is written in the bared basis 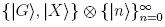 . Thus, it takes the block-diagonal form:
. Thus, it takes the block-diagonal form:
for n-th excitation manifold basis. The eigenvalues can be easily obtained and are given by
where we have defined δ = k + ωα + ω. Note that the eigenvalues of the system depend on both interaction terms, the Fig. 2 shows the dispersion relation vs energy. The effect due to the k is evidenced as a frequency shift and the coupling g behaves accordingly to the well-known Jaynes-Cummings model.
1.1 Lindblad master equation.
To include the effects of the environment is required treat the QD-Cavity system as an open quantum system. It is, to define the Hamiltonians associated to the reservoirs, which is made of electron-hole pairs, photons, phonons and terms associated to a bilinear coupling between the system and reservoirs. The explicit system-reservoir interaction for this model can be found in [8]. After tracing over the external reservoirs degrees of freedom and assuming the validity of the Born-Markov approximation, we obtain the Lindblad master equation for the reduced density matrix, it reads
where the corresponding Lindblad terms for the incoherent processes of dissipation (γ) and pumping (P) follows the rule: 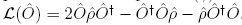 . Where γ is the decay rate due to the loss of photons through the cavity mirrors, and P is the rate at which the excitons are being pumped. The dynamical equations for the populations and coherences in the bared basis are given by
. Where γ is the decay rate due to the loss of photons through the cavity mirrors, and P is the rate at which the excitons are being pumped. The dynamical equations for the populations and coherences in the bared basis are given by
where c.c is used to denote the complex conjugate. Note that we have introduced a short notation for lowest quantum states of the system 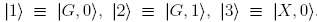 . An schematic representation of the action of the process involved in the dynamics of the system is shown in Fig. 3. It is worth of mentioning that we will consider the lowest excitation manifold for exploring the effects due to non linear optical interaction on both dynamics and photoluminescence spectra.
. An schematic representation of the action of the process involved in the dynamics of the system is shown in Fig. 3. It is worth of mentioning that we will consider the lowest excitation manifold for exploring the effects due to non linear optical interaction on both dynamics and photoluminescence spectra.
1.2 Quantum Regression Theorem and the Emission Spectrum.
When light excites resonantly a QD-Cavity system one of the most important measumerement is the photoluminescence spectrum or so-called emission spectrum of the system. For such task, there are different theoretical approaches in the literature, but frequently this quantity is computed by performing a Fourier transform of the first order correlation function (α† (t + Τ)α(t)), which requires the knowledge of the expectation value of two operators at different times. To obtain the dynamical equation of such correlation function should be applied the Quantum Regression Theorem [6] which states that for an operator O the expectation value of the two-time correlation function (Ô†(t + τ)Ô(t)) satisfies the same equation of motion that as the single-time (Ô(t)) does. Following Porras et. al. in Ref. [8] we obtain that:
where the following definitions has been used:  . It should be noted that these operators act between two consecutive excitation manifolds, and together with our truncation level (first excitation manifold) in the Fock space, it reduces the number of differential equations that are needed for calculating the emission spectrum. Thus, the relevant subset of equations of motion is given by
. It should be noted that these operators act between two consecutive excitation manifolds, and together with our truncation level (first excitation manifold) in the Fock space, it reduces the number of differential equations that are needed for calculating the emission spectrum. Thus, the relevant subset of equations of motion is given by
Particularly, these coupled differential equations can be solved in an exact form, more precisely, we have worked out the solutions and the emission spectrum at the steady-state is given by
where we have defined 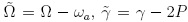 and the density matrix element at the steady-state as
and the density matrix element at the steady-state as 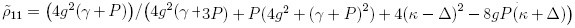 . It should be noted that pn has been calculated in the stationary limit, and it plays the role of the initial condition for the dynamics associated to the emission spectrum.
. It should be noted that pn has been calculated in the stationary limit, and it plays the role of the initial condition for the dynamics associated to the emission spectrum.
1.3 Measurement of entanglement in QD-Cavity systems
One of the most fundamental entanglement measurements for bipartite systems is known as Peres criterion, it states that if the state of bipartite system is separable then the eigenvalues of its partial transpose are all positive. Since our density matrix p has non-zero elements respect to the excitonic subsystem, the density matrix takes the blocks diagonal form 1 x 1 and 2 x 2 when written in the bared basis. We follows Quesada and coworkers in Ref. [9] where they have derived a separability criterion which is equivalent to Peres criterion, and it can detect entanglement in QD-Cavity system. It is,
The evaluation of E(ρ) is in general quite difficult and has to be done numerically.
Results and discussion
2.1 Dynamics
We compare the time evolution of the populations ρ11, ρ22, ρ33 for two different dynamical regimes of the QD-Cavity system. Fig. 4 shows a coherent exchange of energy of quantum dot with the cavity mode, when evidences that the coupling constant g >> γ is the dominant interaction. Thereby, the strong coupling regime exhibits an oscillatory behaviour with some damping as is shown in panel
(a) , in contrast to the weak coupling regime where the interaction of quantum dot with the cavity mode is basically incoherent and dominated by the damping rates, e.g g << γ. Therefore, the weak coupling regime shows an enhanced decay rate as is shown in panel
(b)
2.2 Emission spectrum
We here focus on the emission spectrum of the system and the effects due to the non-linear optical interaction. In Fig. 5 is shown in panel (a) the spectra for k = 0 where is evidenced the typical strong coupling regime in QD-Cavity system. We observe that a frequency shift occurs for the detuning as is shown in panel (b) with k =1. It should noted that the dynamical regime remains without significant changes.
2.3 Entanglement
To quantify the entanglement between quantum dot and cavity we considered the criterion given by Eq. (9) which requires the numerical solution of the density matrix of QD-Cavity system. In Fig. 6 is shown the entanglement as a function of non-linear optical interaction k and time t in the strong coupling regime (a). We found that the entanglement depends strongly on k and shows the typical Rabi oscillations when it is plotted as a function of k and time. Departing from k = ImeV the entanglement increases the frequency of its oscillations, and enhanced its efficiency. It is worth to mention that depending on values of the detuning Δ and k the pattern of the entanglement will shift along k axes. In panel (b) the entanglement versus time is shown for two particular values of k. We found that the phenomena called sudden death of entanglement is evidenced.
2.4 Average number of photons
Since we have pumping and losses processes inside of QD-Cavity system, the average number of photons changes as a result of the competition between those two process, but also the coupling constants affect the dynamics of the system and they promote the creation or annihilation of number of photons. In Fig. 7, we present the evolution of the average number of photons by calculating (â†â) in the stationary limit as a function of coupling constants g and k. We found that the non-linear optical interaction k reduces signficantly the intensity of the light in the cavity. This is due to that is a two-photon interaction and allows transitions that can rapidly populate states with high number of photons, that promptly will leave the cavity.
Conclusions
We found that the non-linear optical interaction (Kerr medium) affects strongly the dynamics of the QD-Cavity system in both weak and strong coupling regimes. The emission spectrum was calculated in an exact form for lowest excitation manifold, and we found that arises a frequency shift in the emission spectrum due to the Kerr medium. In addition, it was examined the influence of Kerr medium on the entanglement of the system as well as on the average photon number.
Acknowledgements
The financial support from Universidad del Quindío for EAG and SEA is gratefully acknowledged. This work has been supported by Colciencias within the project with code 110156933525, contract number 026 - 2013, and HERMES code 17432. Furthermore, HVP acknowledges the technical and computational support of the Grupo de (Optica e Información Cuantica.
References
[1] A. Majumdar, A. Faraon, D. Englund, I. Fushman, and J. Vuckovic, SPIE P. 7211, 72110D (2009).
[2] M. Kauranen and A. V. Zayats, Nat. Photonics 6, 737 (2012).
[3] K. Sakoda, Optical Properties of Photonic Crystals, Springer series in optical sciences (Springer, 2001).
[4] S. Buckley, K. Rivoire, and J. Vuckovic, Rep. Prog. Phys. 75, 126503 (2012).
[5] H. Walther, B. T. H. Varcoe, B.-G. Englert, and T. Becker, Rep. Prog. Phys. 69, 1325 (2006).
[6] D. Walls and G. Milburn, Quantum Optics, Springer Study Edition (Springer Berlin Heidelberg, 2012).
[7] Z. Dan, Z. Xiao-Ping, and Z. Qiang, Chinese Phys. B 22, 064206 (2013).
[8] J. I. Perea, D. Porras, and C. Tejedor, Phys. Rev. B 70, 115304 (2004).
[9] N. Quesada, H. Vinck-Posada, and B. A. Rodríguez, J. Phys. Condens. Mat. 23, 025301 (2011).