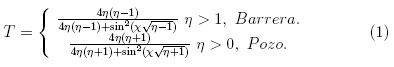
ANÁLOGOS CUÁNTICOS Y ELECTRODINÁMICOS APLICADOS AL SISTEMA ÓPTICO DIELÉCTRICO-SUSTRATO PARA CURSOS DE FÍSICA
LIGHT-ELECTRON WAVE ANALOGY APPLIED TO THE OPTICAL SYSTEM DIELECTRIC-SUBSTRATE FOR PHYSICS COURSES
Jhon H. Vargas1, Raúl E. Castiblanco2, Jhon Morales2
1 Departamento de Física, Universidad Militar Nueva Granada, Bogotá, Colombia.
2 Departamento de Física, Universidad Nacional de Colombia, Bogota, Colombia.
Jhon H. Vargas: jhon.vargas@unimilitar.edu.co
(Recibido: Julio/2016. Aceptado: Septiembre/2016)
Resumen
Se establece la analogía entre la propagación de electrones en pozos cuánticos, con la propagación de ondas electromagnéticas entre medios dieléctricos. Al ser estudiados los fenómenos de transmisión en medios estratificados; pozos o dieléctricos, se encuentran resultados análogos. En primer lugar, se describe la transmitancia para el caso cuántico como electrodinámico. Luego, las relaciones de dispersión mediante los coeficientes de transmisión en ambos casos (electrones-luz) relacionando estos dos sistemas. Y finalmente se compara esta equivalencia con los resultados experimentales en la zona transparente (baja absorción 800-2500 (nm)) del espectro de transmisión de la película delgada de ZnSe, utilizando el método de la matriz de transferencia (MMT).
Palabras clave: Ondas, película delgada, pozo y barrera de potencial, dieléctrico, coeficiente de transmisión, educación.
Abstract
The analogy between the solutions of Schrodinger equation with Helmholtz equation in a dimension is established, mainly of particle propagation (electrons) on quantum wells, with the propagation of electromagnetic waves (light) among electrical means. When transmission phenomena are studied in layered media, wells or dielectrics, they are found in analogical results. In this work, it is first presented the transmittance for quantum case and electrodynamic case independently. Then, the scattering amplitudes are related in both cases (electrons and waves), describing the connection and representation between these two systems. Finally they are compared with the experimental results in the transparent zone (low-absorption 800-2500 (nm)) of ZnSe thin film transmission spectrum, making use of the Transfer Matrix Method (TMM).
Keywords: Waves, thin film, well and barrier potential, dielectric, transmission coefficient, education.
1. Introducción
Con el objetivo de describir los análogos entre los fenómenos cuánticos y electrodinámicos en la propagación de ondas y partículas, se analizan las soluciones de las ecuaciones de Schrodinger y Helmholtz en una dimensión. Estas dos teorías aparentemente independientes (clásicas y cuánticas), tradicionalmente se enseñan como sistemas separados o diferentes, sin embargo, se pueden establecer relaciones importantes entre las mismas, las cuales pueden ser aplicadas en la enseñanza de la Física como también en la caracterización óptica de materiales diekéctricos[1,2].
Al estudiar estos fenómenos a través del método de la matriz de transferencia (MMT) [3-5], es posible visualizar las analogías o relaciones existentes entre el fenómeno de propagación de electrones sobre un potencial cuadrado, atractivo o repulsivo, con los fenómenos de propagación de una onda electromagnética polarizada entre medios dieléctricos bajo incidencia normal.
El presente trabajo, se inicia con la descripción del fenómeno de transmisión de un electrón sobre un pozo o barrera de potencial, describiendo así, los casos ya bien conocidos por la teoría cuántica; como interferencia y efecto túnel[6]. Luego se describe el fenómeno de transmisión de una onda electromagnética plana sobre una placa dieléctrica, en ambos casos a partir del (MMT), y finalmente se establecen analogías entre los casos mencionados anteriormente[5]. Una vez descritos los fenómenos de transmisión para los casos óptico y cuántico, se obtiene el espectro de transmisión para un sistema óptico aire-vidrio-aire a partir de su análogo cuántico, obteniendo los mismos resultados que los reportados por el grupo GALIFA[2]. Posteriormente, se compara con la transmisión obtenida experimentalmente del mismo sistema en la zona de baja absorción de la película delgada semiconductora ZnSe, es decir, con longitudes de onda (λ) incidentes desde 800 (nm) hasta 2500 (nm), confirmando indirectamente la validez experimental de la equivalencia o analogía entre la ecuación de Schrodinger y Helmholz.
2. Transmisión para el Pozo y la Barrera de Potencial
A partir del (MMT) se pueden calcular los coeficientes de transmisión para una partícula incidente sobre una barrera o pozo de potencial, este método consiste en escribir la continuidad de la función de onda y su derivada en cada interface, obteniendo un sistema de dos ecuaciones por cada una de las fronteras o discontinuidades del potencial, y de este modo, se trabajan las amplitudes incidentes y transmitidas en términos de una matriz llamada Matriz de Transferencia, en donde, el inverso de la norma al cuadrado del elemento α11 corresponde al coeficiente de transmisión. A partir de este cálculo, se encontró que los coeficientes de transmisión para una barrera y un pozo de potencial son [6]:
donde 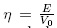 es una
relación de energía, y
es una
relación de energía, y 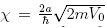 es la opacidad de la barrera o pozo. La figura 1, muestra el coeficiente de transmisión en
términos de la energía incidente con respecto al potencial η, con x = 15, tanto para el pozo como para la barrera.
es la opacidad de la barrera o pozo. La figura 1, muestra el coeficiente de transmisión en
términos de la energía incidente con respecto al potencial η, con x = 15, tanto para el pozo como para la barrera.
En esta se
puede observar que la transmisión tiene máximos y mínimos
debidos a la diferencia de caminos entre las múltiples reflexiones que
existen en el interior de barrera o pozo, es decir, interferencia tipo Fabrit-Perot,
en donde, los máximos se pueden calcular en el caso de la barrera con 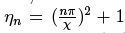 , siendo n el valor entero para el cual la barrera es completamente transparente. En el
caso del pozo de potencial con
, siendo n el valor entero para el cual la barrera es completamente transparente. En el
caso del pozo de potencial con 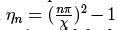 , la interferencia de la barrera sucede
cuando la energía E del electrón es mayor al potencial V0, de lo contrario no hay interferencia, si no, efecto túnel; en el
caso del pozo siempre ocurriría interferencia, ya que E > 0 > V0 [6-8].
, la interferencia de la barrera sucede
cuando la energía E del electrón es mayor al potencial V0, de lo contrario no hay interferencia, si no, efecto túnel; en el
caso del pozo siempre ocurriría interferencia, ya que E > 0 > V0 [6-8].
3. Transmisión de una onda electromagnética a través de una placa dieléctrica
Cuando sobre una placa dieléctrica de espesor d, incide normalmente una onda electromagnética plana polarizada (TE). Los índices de refracción de los tres medios no permeables son n1, n2, n1. Ahora bien, para calcular el coeficiente de transmisión, y debido a que la onda esta polarizada de tal manera que la incidencia de los campos es normal, solamente las componentes normales a la interface establecen la continuidad de los campos. A partir de estas, se encuentra que el coeficiente de transmisión en términos de la longitud de onda (λ), esta dada por:
esta
ecuación muestra el resultado esperado, ya que el termino sin2 (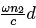 ) describe un
patrón de interferencia que depende del espesor de la placa y de la
longitud de onda incidente, de la siguiente manera:
) describe un
patrón de interferencia que depende del espesor de la placa y de la
longitud de onda incidente, de la siguiente manera:
a) Cuando λ ∼ 2πn2d, (película delgada) existe interferencia Fabrit-Perot. Que en su forma esta descrita por (2).
b) Cuando
λ << 2πn2d, (película gruesa-sustrato) deja
de existir interferencia y la transmisión se mantiene constante. La
transmitancia se calcula a través del promedio de la función (sin2 (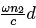 )), cuyo
período está dado por
)), cuyo
período está dado por 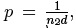 , este promedio se puede encontrar con la
integral:
, este promedio se puede encontrar con la
integral: 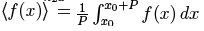 para una
función armónica en el tiempo f (x).
para una
función armónica en el tiempo f (x).
El comportamiento de la transmitancia para ambos casos en términos de la longitud de onda λ es representado en la figura 2.
Se puede apreciar cómo se obtiene un patrón de interferencia para el caso de película delgada a) y una transmitancia constante para el caso de película gruesa b) o sustrato de vidrio de un milímetro de espesor, reportado como 0.92 [2].
4. Equivalencia entre los casos electrodinámicos y cuánticos
A partir de los casos descritos es posible establecer relaciones entre los fenómenos de propagación de ondas o partículas según sea el caso cuántico o electrodinámico. Para establecer formalmente dichas relaciones se tiene las siguientes analogías:
■ (i) Sí la permitividad eléctrica de la placa ε2 es mayor que la permitividad del medio incidente y transmitido, es decir, ε2 > ε1, este fenómeno cumple el mismo rol de una partícula incidente sobre un pozo de potencial.
■ (ii) Sí ε2 < εi, este problema es análogo a una partícula incidiendo sobre una barrera de potencial.
4.1. Onda Plana Incidente Sobre una Interfase Dieléctrica y su Análogo Cuántico
Se considera ahora la propagación de una onda electromagnética plana con incidencia oblicua (θ) sobre una interfase dieléctrica, viajando entre dos medios caracterizados por diferentes permitividades (ε1, ε2) y permeabilidades (µ1= µ2 = 1).
El sistema de coordenadas se fija sobre la interfase que es perpendicular al eje z, la dirección de propagación de la onda electromagnética es perpendicular al eje y, la geometría de este problema es mostrado en la figura 3, en donde, el vector de onda solo tiene dos componentes k = (kx, 0,kz).
Para
encontrar los análogos, es necesario establecer primero las condiciones
de frontera sobre la interfase, y ya que las componentes tangenciales de los
vectores de onda son continuos, es decir, 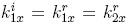 , los vectores de onda para cada medio se
pueden expresar como [5]
, los vectores de onda para cada medio se
pueden expresar como [5]
restando las anteriores ecuaciones se encuentra
para el caso de la barrera de potencial se tienen los vectores de onda k, q respectivamente,
y su diferencia
entonces, la equivalencia se establece igualando (4) con (6), y se obtiene la primera analogía:
Este resultado es obtenido al comparar la ecuación de onda de Helmholtz con la ecuación de onda de Schrodinger, en donde, la discontinuidad en el potencial que presencia la partícula al propagarse de un medio a otro, es equivalente a la diferencia de permitividades que presencia la onda electromagnética al propagarse entre dos medios dieléctricos diferentes. Para establecer la relación de la energía incidente de la onda, se compara la relación de dispersión en la dirección z, para ambas regiones. Igualando las ecuaciones (3) y (5) se obtiene como resultado la segunda analogía:
ahora
definiendo los parámetros adimensionales vistos en el sección dos 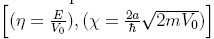 , con su
equivalente electrodinámico, y dividiendo las ecuaciones
(8) entre (7) se encuentra así la tercera
analogía:
, con su
equivalente electrodinámico, y dividiendo las ecuaciones
(8) entre (7) se encuentra así la tercera
analogía:
haciendo
uso de la ley de Snell, se puede conocer la componente del vector de onda k1x,
como 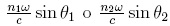 y bajo incidencia
normal se tiene que θ1,2 =0, y por ende este
término se anula de la anterior relación. Finalmente para
encontrar el parámetro x, se despeja V0 de la ecuación
(7), y se reemplaza en la definición de x para el caso
cuántico encontrando la cuarta analogía:
y bajo incidencia
normal se tiene que θ1,2 =0, y por ende este
término se anula de la anterior relación. Finalmente para
encontrar el parámetro x, se despeja V0 de la ecuación
(7), y se reemplaza en la definición de x para el caso
cuántico encontrando la cuarta analogía:
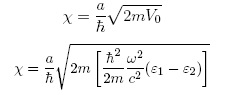
con α =d para el espesor de la barrera en el caso óptico se tiene
las analogías descritas en los apartados anteriores son mostradas en la Tabla 1.
Definidas estas relaciones, estas pueden ser comprobadas desde un punto de vista teórico, si se toma el resultado de transmisión para el caso cuántico y se sustituye en el los análogos ópticos η,y x, se llega al mismo resultado tradicionalmente resuelto desde las ecuaciones de Maxwell.
Como un
primer ejemplo, a continuación se calcula el coeficiente de
transmisión para el caso óptico utilizando los resultados de la
barrera de potencial, donde 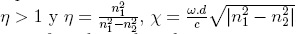 , como n1 > n2,
el valor absoluto
, como n1 > n2,
el valor absoluto 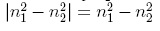 . Al reemplazar
términos en la ecuación (1).
. Al reemplazar
términos en la ecuación (1).
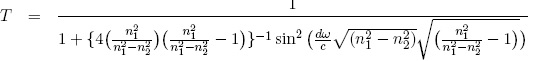
que es justamente la ecuación (2)
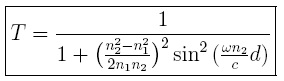
A partir
del pozo donde 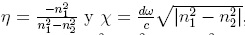 , como en este caso
n1 < n2, el valor absoluto
, como en este caso
n1 < n2, el valor absoluto 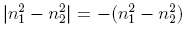 , ahora
reemplazando nuevamente en (1).
, ahora
reemplazando nuevamente en (1).
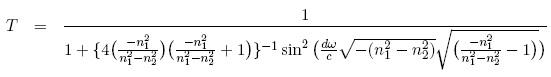
lo que finalmente conduce a la misma ecuación (2)
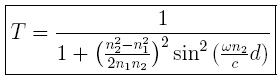
Estos resultados son equivalentes con el caso Óptico, y aunque la forma matemática es idéntica, la física de los fenómenos involucrados es completamente distinta; el espectro de transmisión para un pozo o barrera de potencial depende de la energía E de la partícula incidente sobre dicho potencial, por otro lado, el patrón de interferencia para el caso óptico depende de la relación del espesor de la placa con la longitud de onda incidente. Cuando el orden de estas es comparable existe interferencia (película delgada), en el caso contrario el valor para la transmisión permanece constante (película gruesa).
Si se varia el ángulo de incidencia sobre la placa dieléctrica, permaneciendo constante la longitud de onda se obtiene el patrón de interferencia Fabrit-Perot para ángulos menores al ángulo crítico, y efecto túnel o transmisión nula para ángulos mayores al ángulo crítico, de forma análoga a la barrera para energías mayores y menores al potencial respectivamente[5].
5. Aspectos Teóricos - Experimentales
Como una aplicación se modela el sistema óptico aire-película-sustrato-aire, se calcula el coeficiente de transmisión y se muestran dos casos experimentales; su análogo cuántico es mostrado en la Figura 4.
A partir de las condiciones de frontera de la función de onda proveniente de la ecuación de Shrodinger, y de los vectores de onda en cada una de las regiones, se puede escribir la matriz de transferencia como:
y luego de
realizar los respectivos productos matriciales para hallar el elemento que
relaciona la transmisión, es decir, 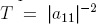 . Simplificando con el uso de la tabla 1, el coeficiente de transmisión toma la forma:
. Simplificando con el uso de la tabla 1, el coeficiente de transmisión toma la forma:
observe que los términos promediados son los senos y cosenos que describen la transmisión dada por el sustrato de espesor b, y sin promediar los términos asociados a la película delgada de espesor α. A continuación en la figura 5, se muestra la transmisión para diferentes valores de espesores α, e índices de refracción reportados por GALIFA[2].
Al encontrar los respectivos valores medios y graficando la ecuacion (12) con respecto a la longitud de onda incidente (λ), se obtiene la siguiente figura 5.
Ahora bien, aplicando el resultado teórico a medidas de transmitancia registradas en el laboratorio para la caracterización óptica de una película delgada de ZnSe, se busca modelar el espectro obtenido por métodos experimentales a través de la ecuación (12), con rangos de longitudes de onda incidentes de 800 a 2500 (nm), donde el valor del coeficiente de extinción ks del vidrio o sustrato es prácticamente nulo y teniendo en cuenta un comportamiento cuasi-constante para el índice de refracción de la película semiconductora y un débil coeficiente de absorción (α), se concluye que tanto la constante dieléctrica e y el correspondiente índice de refracción a estas frecuencias pueden considerarse reales y aproximadamente constantes [2] [9], la Figura 6 presenta los espectros de transmisión experimental y teórico.
6. Conclusiones
Se encontró que al describir la propagación de partículas y ondas sobre diferentes medios, clásicos o cuánticos se puede llegar a modelos análogos; se mostró que la escritura de los coeficientes de transmisión para estos dos sistemas son idénticos en su forma, aunque difieren en su interpretación Física. Desde el punto de vista cuántico los espectros de transmisión de electrones sobre una barrera de potencial dependen directamente de la energía con la cual inciden las partículas, obteniendo un patrón de interferencia para valores mayores al potencial de la barrera, y efecto túnel, para energías menores al potencial.
Clásicamente la transmisión de una onda electromagnética sobre una placa dieléctrica depende del ángulo con el cual se incide la onda y no directamente de la energía (manteniendo constante la longitud de onda). Así como el valor del potencial es un valor crítico V0 en el caso cuántico, análogamente para una placa dieléctrica en el caso óptico existe un ángulo crítico, donde para valores menores a este, existe transmisión e interferencia y en caso contrario para valores mayores no existiría transmisión, aunque es probable que ocurra efecto túnel para el caso electromagnético. Se concluye que para ambos sistemas, el análogo es válido ya que al comparar con medidas experimentales de transmisión sobre una película delgada de ZnSe se obtiene el valor esperado del índice de refracción para este material en estas longitudes de onda n2 = 2,68. También se obtuvo una relación válida para el coeficiente de transmisión paralelo al deducido por el grupo GALIFA de la Universidad de Barcelona, con la diferencia que el deducido en el presente trabajo se hizo a partir del método de la matriz de transferencia (MMT) presentando la ventaja que está caracterizará todo el espectro de transmisión sin limitantes de frecuencias incidentes.
Referencias
[1] J. Torres, J. Cisneros, G. Gordillo, and F. Alvarez, Thin Solid Films 289, 238 (1996).
[2] GILAFA, "Laboratorio de física de materiales dielectricos y Ópticos," (2016), Universidad de Barcelona.
[3] A. Z. Khachatrian, Armenian J. Phys. 3, 064206 (2010).
[4] P. Yeh, Optical Waves in Layered Media, Wiley Series in Pure and Applied Optics (Wiley, 2005).
[5] P. Markos and C. Soukoulis, Wave Propagation: From Electrons to Photonic Crystals and Left-Handed Materials (Princeton University Press, 2008).
[6] J. H. Vargas, R. E. Castiblanco, M. Córdenas, and J. Morales, Momento 42, 23 (2011).
[7] L. Jelinek, J. D. Baena, J. Voves, and R. Marques, New J. Phys. 13, 083011 (2011).
[8] I. Hrebikova, L. Jelinek, J. Voves, and J. Baena, Photonics Nanostruct. 12, 9 (2014).
[9] R. Castiblanco, Estudio de Cristales Fotonicos en 1D a través del Método de Matriz de Transferencia, Tesis de maestría, Universidad Nacional de Colombia, Bogotá - Colombia (2013).