
DELINQUIR O NO DELINQUIR. UN MODELO DE REDES DELINCUENCIALES Y UN ALGORITMO PARA SU ANÁLISIS
TO COMMIT OR NOT TO COMMIT A CRIME. A CRIMINAL NETWORK MODEL AND AN ALGORITHM FOR ITS ANALYSIS
Fredis Agámez, John F. Cantillo, Javier Montoya, John E. Realpe
Grupo de Modelado Computacional (GruMoC), Instituto de Matemáticas Aplicadas, Universidad de Cartagena, Colombia.
Fredis Agámez: fagamezg@unicartagena.edu.co
(Recibido: Septiembre/2016. Aceptado: Enero/2017)
Resumen
En este trabajo se propone e investiga un modelo matemático de redes delincuenciales. Este problema se formula en el marco de la teoría de juegos, uno de cuyos conceptos principales es el de equilibrio de Nash. Se discute como el problema de encontrar un equilibrio de Nash da lugar a un problema de satisfacción de restricciones y cómo este se puede analizar usando métodos de la mecánica estadística, cuya formalización matemática es un tema de investigación muy activo en la actualidad. Desde el punto de vista computacional, tales métodos dan lugar a algoritmos de paso de mensajes que permiten obtener propiedades estadísticas de interés, tales como el nivel de actividad delincuencial promedio y el número de equilibrios de Nash.
Palabras clave: Sistemas complejos, teoría de juegos, modelado computacional, modelos en redes, teoría de probabilidad, redes delincuenciales, mecánica estadística.
Abstract
Here we introduce and investigate a mathematical model of delinquent networks. This problem is formulated in the framework of game theory, one of whose main concepts is the Nash equilibrium. We discuss how the problem of finding a Nash equilibrium leads to a constraint satisfaction problem, and how it can be analyzed using methods of statistical mechanics whose mathematical formalization is a very active research topic today. From the computational point of view, such methods give rise to algorithms of passage of messages that allow to obtain statistical properties of interest, such as the level of average delinquency activity and the number of Nash equilibria.
Keywords: Complex systems, game theory, computational modeling, networks models, probability theory, delinquent networks, statistical mechanics.
En la actualidad las fronteras entre las disciplinas se tornan cada vez más tenues a medida que se reconoce el carácter interdisciplinar de los diversos fenómenos que ocurren en nuestro entorno. Es así como hoy por hoy las llamadas "ciencias duras", tales como la matemática y la física, cada vez extienden más su rango de aplicación consolidando un conjunto de técnicas y conceptos que se han venido agrupando en la denominada teoría de sistemas complejos. Todo esto adquiere aún más relevancia con la creciente capacidad de adquisición de datos reales [1, 2] que, debido a su inmenso potencial, han recibido el apelativo de "el nuevo petróleo"[3]. Así mismo esto constituye una importante oportunidad para los países en vía de desarrollo de apoyar decididamente las ciencias básicas al mismo tiempo que se buscan soluciones a problemas urgentes de una nación, lo que usualmente son percibidos como objetivos opuestos que compiten por los recursos limitados de ésta. El estudio de fenómenos socioeconómicos, como lo son la delincuencia y la corrupción, desde la perspectiva de las ciencias de la complejidad son un ejemplo de ello [4, 5].
En efecto, una red delincuencial puede ser vista como un sistema de múltiples agentes interactuantes que puede formularse dentro del marco conceptual de la teoría de juegos [6]. En esta teoría se asume que los agentes son autónomos y que pueden tener objetivos conflictivos, de modo que cada agente busca obtener lo mejor para sí condicionado al comportamiento estratégico de los demás agentes, y condicionando a su vez, el comportamiento de los mismos [6, 7]. Las diferentes estrategias que un agente puede asumir pueden representarse por variables numéricas, y las preferencias de un agente dado pueden codificarse en una función de utilidad, o matriz de pagos, la cual asigna un número a cada configuración de estrategias del agente en cuestión y de la de los demás agentes involucrados. Una configuración de estrategias en la cual todos los agentes están satisfechos, en el sentido de que ninguno tiene un incentivo unilateral (de acuerdo a sus preferencias) de cambiar de estrategias, se conoce como equilibrio de Nash, y constituye el concepto de solución en el cual se concentra este trabajo.
En este estudio se investiga un modelo de redes delincuenciales que consiste de un conjunto de individuos situados en los nodos de una red que pueden decidir si delinquir o no. Un vínculo entre un par de nodos en esta red indica que los individuos correspondientes tienen una influencia mutua en sus decisiones. Las preferencias de un agente dado están codificadas en su función de pagos, la cual representa la relación costo-beneficio caracterizada por el balance entre las ganancias obtenidas de su actividad criminal y las consecuencias de que sea capturado. El modelo se construye en analogía con un modelo propuesto recientemente en la literatura de las ciencias socioeconómicas [8] e investigado por algunos de los autores en Bahoque et al. [9]). La principal diferencia reside en el tipo de información que se tiene sobre el sistema. En efecto, mientras que en Ballester et al. [8] se asume que se conoce el nivel de actividad delincuencial de cada individuo en la red, el cual se modela como un número real que podría estimarse, por ejemplo, con la frecuencia con la que un individuo dado delinque en una cierta ventana de tiempo, aquí se asume una situación que puede considerarse más realista en la cual solo se tiene información sobre si un determinado individuo delinque o no. Desde un punto de vista matemático, hay una diferencia importante entre trabajar con variables reales y trabajar con variables discretas, en esta caso binarias (delinquir o no). En efecto, en el primer caso se puede recurrir a las técnicas analíticas del cálculo, mientras que el segundo caso corresponde a un problema combinatorio mías cercano a la lógica subyacente a la ciencia de la computación.
Recientemente se ha encontrado que los métodos matemáticos y computacionales de la mecánica estadística, que inicialmente podrían entenderse como una colección de ideas heurísticas, resultan muy efectivos para el análisis de problemas combinatorios de diversa índole [10]. Este éxito, a su vez, ha atraído gran interés por parte de los matemáticos, quienes han venido contribuyendo a formalizar estas ideas sobre bases matemáticas solidas [11-14]. En el caso de las redes delincuenciales que se estudian en este trabajo, dicha conexión con la mecánica estadística surge al considerar el sistema de agentes como un sistema de partículas que interactúan entre sí. El estado de una de tales partículas corresponde a la estrategia del agente que representa, y a cada configuración de estrategias se le puede asociar una función de energía apropiada, de manera que las configuraciones de interés, como por ejemplo los equilibrios de Nash, correspondan a las configuraciones de mínima energía. Una vez se tiene este mapa, el problema se traduce en el estudio de la distribución de Boltzmann asociada a dicho sistema de partículas. Uno de los métodos mías importantes para el estudio de la distribución de Boltzmann de sistemas definidos sobre grafos es conocido como el método de la cavidad, el cual puede interpretarse como un marco conceptual que facilita el desarrollo de algoritmos de paso de mensajes [15-17].
En la siguiente sección se introduce el modelo a estudiar y se define el problema de encontrar un equilibrio de Nash como un problema de satisfacción de restricciones. En la sección 4 se discute como los métodos matemáticos y computacionales de la mecánica estadística pueden utilizarse para el análisis de este problema. Esta sección puede tomarse como una introducción a estas ideas que se han venido constituyendo en un airea de estudio importante de las matemáticas en la actualidad. Finalmente, en las secciones 6 y 7 se presentan los resultados obtenidos y las conclusiones del estudio, respectivamente.
2. Definición del modelo: Delinquir o no delinquir
Como se mencionó anteriormente, el modelo aquí propuesto se basa en el modelo de Ballester et al. [8] que ha sido estudiado recientemente en Bahoque et al. [9]. Sin embargo en este trabajo, en contraste con el modelo de Ballester et al, las variables son binarias y por lo tanto se deben utilizar otro tipo de técnicas, mías cercanas a la matemática discreta, que están siendo desarrolladas activamente en la actualidad. La presentación del modelo sería por lo tanto necesariamente similar a la de [9] aunque en el proceso se enfatizarían algunas diferencias. Estudios preliminares sugieren que la topología de las redes delincuenciales se aproxima a la de las redes complejas [18], sin embargo, aquí se utilizaron grafos aleatorios con el fin de simplificar este primer estudio sobre el tema. También es importante anotar que nuestro método es independiente de la interpretación que se le pueda dar a cada parámetro, pero conociendo relaciones causales entre aquellas características específicas que representan los parámetros y las variables de salida del modelo tendríamos capacidad de predicción y de control.
Una red delincuencial g se define mediante un conjunto N = {1,..., n} de individuos idénticos y un conjunto de vínculos entre ellos. Esta se puede describir asociando una variable binaria gij a cada par de individuos i y j en la red, tal que gij = 1 si y solo si i y j interactúan, o se influencian, directamente, y gij = 0 de otro modo. La matriz G con componentes gij se conoce como la matriz de adyacencia de la red. Cada individuo i en la red tiene asociada una variable binaria xi tal que xi = 1 si el individuo delinque y xi = 0 en caso contrario. Se denotara por x = ... ,xn} una asignación de estas variables binarias para toda la red. En analogía con Ballester et al. [8], la ganancia esperada para el individuo i, si este delinque, está dada por la expresión

donde

corresponde a la ganancia bruta del individuo i, que depende de si este delinque o no, y del perfil delincuencial de la población. Por otra parte,

se refiere a la "perdida" debido a la posibilidad de que el individuo i sea capturado. Dicha ganancia o utilidad depende no solo de la estrategia adoptada por el individuo en consideración, sino también del esfuerzo de todos los demás individuos y de la estructura de la red. Esto se debe a la competencia global por recursos limitados y a la colaboración local entre individuos. Aquí p0 está relacionado con probabilidad de que un individuo genérico sea capturado, δ > 0 se relaciona con la intensidad de la competencia global, y φ ≥ 0 modela la intensidad de la colaboración y complementariedad local entre los individuos para evitar la aprehensión. Al producto p0 ƒ lo llamaremos πo, correspondiendo al parámetro que modela la intensidad de las sanciones impuestas.
3. Equilibrio de Nash y satisfacción de restricciones
De acuerdo a la hipótesis de racionalidad de la teoría de juegos, los individuos escogen la estrategia xi (delinquir o no) que maximice su utilidad ui(x), dados las estrategias escogidas por los demás individuos x-i = {x1,..., xi-1, xi+1,..., xn}. Así pues, todos los individuos estarán satisfechos en la configuración x* = {x1,..., xn}
si
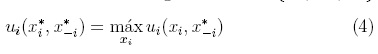
En este caso, dicha configuración se conoce como un equilibrio de Nash puro. El cualitativo de "puro" se refiere a que se están considerando las estrategias delinquir o no, en contraste con estrategias "mixtas" que consisten en delinquir o no con una cierta probabilidad. Si bien está garantizado que un equilibrio de Nash mixto siempre existe, no se puede decir lo mismo de un equilibrio de Nash puro. Por otra parte, los equilibrios de Nash no son necesariamente únicos. Por esta razón una de las cantidades a estudiar sería el número de equilibrios de Nash puros como función de los parámetros del modelo.
Una configuración x* es un equilibrio de Nash si se satisfacen las n restricciones dadas por la expresión [4]. Este tipo de sistemas se conocen como problemas de satisfacción de restricciones y son de gran relevancia práctica. Introduciendo la función indicador 1 [p], la cual es igual a 1 si la proposición p es verdadera e igual a 0 de otro modo, la condición de Nash se puede escribir como:
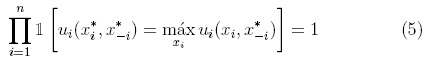
Propiedades típicas del sistema pueden calcularse a partir de la probabilidad de que una configuración escogida al azar sea un equilibrio de Nash

donde la constante de normalización
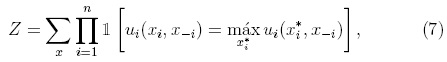
coincide con el número de equilibrios de Nash en el sistema.
4. Construcción de un sistema físico equivalente
Esta formulación guarda una estrecha relación con la mecánica estadística, y esta simple observación ha abierto toda un aérea de investigación sobre la aplicación de los métodos matemáticos y computacionales de esta a un gran número de aplicaciones en diversas disciplinas [15, 19]. Esto ha motivado la formalización matemática de algunos potentes métodos heurísticos desarrollados en el estudio de la mecánica estadística, tales como el celebrado método de la cavidad [11-17]. Por esta razón vale la pena tener una idea más clara de dicha conexión con la mecánica estadística. En particular, la aplicación del método de la cavidad a la búsqueda de equilibrios de Nash en juegos sobre redes fue explorada por uno de los autores [20], y es el método que ha sido empleado en esta investigación.
La idea es simple: a cada configuración se le asocia una función de energía apropiada de manera que las configuraciones de interés, en este caso los equilibrios de Nash, correspondan a las configuraciones de mínima energía [10, 20]. Así pues dicha función de energía puede definirse en este caso como

donde

en consecuencia, E(x) = 0 si y solo si x es un equilibrio de Nash, y este corresponde al valor mínimo.
Una vez que el espacio de configuraciones y la función de energía son fijados, la probabilidad Pβ(x) para que el sistema se encuentre en la configuración x está dada por la distribución de Boltzmann [15],

donde β es un parámetro que en aplicaciones a la física corresponde al inverso de la temperatura, excepto por una constante, y la constante de normalización

se conoce como función de partición. Las propiedades estadísticas del sistema se pueden estudiar mediante el estudio de dicha función de partición [15], la cual juega un rol de función generante [20]. Finalmente, si se nota que en el límite β - ∞ se tiene

y que la
condición  corresponde a la
condición de Nash, se puede concluir que
corresponde a la
condición de Nash, se puede concluir que

y que la constante de normalización lím β→∞ ZB (β) = Z coincide con el número de equilibrios de Nash (7).
Si bien esto puede parecer una trivialidad, y el parámetro β absolutamente innecesario, esta analogía entre la mecánica estadística y los problemas matemáticos de origen combinatorio ha dado lugar al algoritmo de recocido simulado, uno de los más utilizados desde su incepción [19]. En este el parámetro β juega un rol fundamental. En la última década otro método inspirado en la mecánica estadística que ha dado lugar a algoritmos más potentes que el de recocido simulado [10] y que ha atraído gran interés por parte de los matemáticos [11-14] es precisamente el método de la cavidad que se discutirá a continuación [15-17, 21, 22].
5. Método de la cavidad para redes delincuenciales
El problema de caracterizar los equilibrios de Nash del sistema está estrechamente relacionado con el cálculo de la función de partición Z. Uno de los métodos más efectivos para tratar con este tipo de problemas es el llamado método de la cavidad. Este método se puede interpretar como un algoritmo de paso de mensajes, donde cada nodo en la red recoge información de sus nodos vecinos, realiza un cálculo con esta, y reenvía la información actualizada de nuevo a cada uno sus vecinos [15, 23]. De una manera mas general, el problema consiste en calcular una suma de la forma

donde la
función que se está sumando se puede escribir como un producto de
M factores  , donde cada factor
ψa sólo depende de un subconjunto de variables denotado
como xa. En el caso de las redes delincuenciales aquí
estudiadas, hay un factor ψi por cada variable i y está
dado por la función indicador que verifica la condición de Nash
para el individuo i, y la función ψ es el producto de los n
factores, como puede observarse en la ecuación (7).
El método de la cavidad explota la estructura de dicha
factorización. Más específicamente, la función
ψ se puede representar como un grafo bipartito donde a cada factor ψa se le asocia un tipo de nodo (representados, por ejemplo, por cuadrados) y a
cada variable xi se le asocia otro tipo de nodo (representados, por
ejemplo, por círculos). En este grafo bipartito un vínculo entre
factor ψa y una variable xi indica que este factor
depende de dicha variable. No existen vínculos ni entre factores ni
entre variables, lo que le da su carácter de bipartito (ver Figura
1). Dicho grafo usualmente se denomina grafo de factores
[23].
, donde cada factor
ψa sólo depende de un subconjunto de variables denotado
como xa. En el caso de las redes delincuenciales aquí
estudiadas, hay un factor ψi por cada variable i y está
dado por la función indicador que verifica la condición de Nash
para el individuo i, y la función ψ es el producto de los n
factores, como puede observarse en la ecuación (7).
El método de la cavidad explota la estructura de dicha
factorización. Más específicamente, la función
ψ se puede representar como un grafo bipartito donde a cada factor ψa se le asocia un tipo de nodo (representados, por ejemplo, por cuadrados) y a
cada variable xi se le asocia otro tipo de nodo (representados, por
ejemplo, por círculos). En este grafo bipartito un vínculo entre
factor ψa y una variable xi indica que este factor
depende de dicha variable. No existen vínculos ni entre factores ni
entre variables, lo que le da su carácter de bipartito (ver Figura
1). Dicho grafo usualmente se denomina grafo de factores
[23].
Ahora bien, el método de la cavidad parte de la hipótesis de que el grafo de factores tiene la topología de un árbol, es decir que no existen ciclos, o mejor que no es posible partir de algún nodo en el grafo, caminar por esté a través de los vínculos, y llegar de nuevo al punto de partida sin nunca haber repetido un vínculo. En la Figura 1 notamos que si se retira un nodo factor del grafo y los vínculos correspondientes, esté se descompone en tres subgrafos completamente independientes y nuevamente con la topología de un árbol. Esta propiedad de independencia se debe precisamente a la topología de árbol del grafo original, y como puede verse los sub-grafos obtenidos heredan dicha estructura. Esto permite aplicar la misma idea de manera recursiva para obtener una solución del problema de manera eficiente, a partir de las soluciones de las siguientes ecuaciones [15, 23, 24] (ver Figura 1)
donde u→i pasa
información parcial de la rama que contiene el factor a pero no contiene
el nodo i, normalizada de manera que  . Así mismo ηi→α pasa
información parcial de la rama que contiene el nodo i pero no contiene
el factor a, normalizada de manera que
. Así mismo ηi→α pasa
información parcial de la rama que contiene el nodo i pero no contiene
el factor a, normalizada de manera que  . Las constantes
. Las constantes  se escogen de
manera que garanticen la normalización de los mensajes ua→i y ηi→α para todo
vínculo (i, a).
se escogen de
manera que garanticen la normalización de los mensajes ua→i y ηi→α para todo
vínculo (i, a).
Una vez se solucionan estas ecuaciones se pueden obtener los marginales asociados a una variable o a un factor así:


donde las constantes ζi y ζα garantizan la correcta normalización de dichas distribuciones de probabilidad- Este resultado puede asimilarse de manera intuitiva observando que los marginales simplemente recogen toda la información que llega al nodo en consideración, con el detalle adicional que en el caso de un nodo factor a se debe adicionar el factor mismo ψα ya que este no ha sido tenido en cuenta por los mensajes que llegan a dicho factor. A partir de estos marginales se pueden calcular cantidades de interés como el número promedio de individuos que delinquen y la entropía
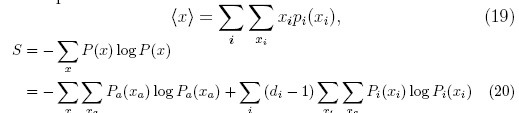
El conjunto de ecuaciones 15 y 16 puede resolverse inicializando los mensajes con valores positivos al azar y luego iterando dichas ecuaciones hasta converger a un punto fijo. En el caso de que el grafo de factores tenga la topología de un árbol, este método converge a un único punto fijo en un numero de iteraciones dado por el diámetro del árbol, es decir la mayor distancia, o número de vínculos, que existe entre cualquier par de nodos en el grafo [15].
Aunque el método de la cavidad se define con referencia a un árbol, parte del gran interés que ha despertado se debe a que su aplicación a grafos más generales con ciclos funciona sorpresivamente bien. La intuición detrás del éxito del método de la cavidad es que si los ciclos en un grafo dado son lo suficientemente largos y si las correlaciones entre pares de variables en este decaen lo suficientemente rápido con la distancia, o número de vínculos entre las variables, entonces las ecuaciones de la cavidad 'ven' efectivamente un árbol. En otras palabras, en la práctica los mensajes 'convergen', en un sentido aproximado, en un número de iteraciones relativamente corto y la variabilidad en estos después de dicho punto puede ignorarse. Así pues, el método de la cavidad tal y como se ha presentado puede aplicarse también a grafos con ciclos, si bien en este caso ya no habría garantías de convergencia ni de precisión en los resultados. En este sentido debe entenderse como un método heurístico que en la práctica usualmente funciona bastante bien. Antes de poder aplicar el método de la cavidad al problema de redes delincuenciales se debe tener en cuenta un par de detalles adicionales que se describirían a continuación.
Por una parte, en la Figura 2a se muestra el grafo de factores que corresponde al problema de satisfacción de restricciones asociado a la condición de equilibrio de Nash para una red delincuencial con la topología de un árbol. Como se puede observar dicho grafo de factores no hereda la misma topología de árbol debido a la existencia de ciclos pequeños de cuatro vínculos que unen cualquier par de variables. Este problema se puede resolver si se agrupan pares de variables de nodos vecinos en nuevas variables, como se muestra en la Figura 2b. En este caso la topología del grafo de factores equivalente es la de un árbol, al costo de que ahora los mensajes en consideración dependerán de dos variables, y no de una como era el caso descrito en la sección anterior [20].
Por otra
parte, como se puede observar en la Figura 2 la
función de utilidad de cada individuo depende de las estrategias de
todos los individuos en la red a través de la suma  . Esto implica que
cada factor en el grafo de factores asociado dependerá a su vez de todas
las variables del problema. Por lo tanto, incluso si se considera una red
delincuencial con la topología de un árbol y se agrupan las
. Esto implica que
cada factor en el grafo de factores asociado dependerá a su vez de todas
las variables del problema. Por lo tanto, incluso si se considera una red
delincuencial con la topología de un árbol y se agrupan las
variables
por pares como se describió anteriormente, el grafo de factores asociado
no heredará aún la topología de árbol de la red
delincuencial. Sin embargo, esto se puede resolver de una manera aproximada
aprovechando el hecho de que dicha dependencia no es arbitraria sino que cada
factor depende de todas las variables a través de una cantidad agregada,
es decir la suma de todas las variables. En este caso se puede asumir que se
conoce el valor de dicha suma c =  . Condicionado al valor de dicha suma el
grafo de factores hereda la topología de árbol
[25]. La aproximación aparece en el modo de escoger c. El modo más elemental de hacerlo es reemplazando en (2)
. Condicionado al valor de dicha suma el
grafo de factores hereda la topología de árbol
[25]. La aproximación aparece en el modo de escoger c. El modo más elemental de hacerlo es reemplazando en (2)
Otra posibilidad sería escoger de manera auto-consistente el valor de c por su promedio (x) calculado con los mensajes en cada iteración. Este último método, implementado originalmente en [20], no arrojó resultados aceptables en este caso y por eso esta investigación se concentro en el método descrito por la ecuacioún (21), dejando para futuros estudios la exploración de otros métodos más precisos.
6. Resultados
En esta sección se presentan los resultados obtenidos mediante la solución iterativa de las ecuaciones de la cavidad para redes delincuenciales, descritas anteriormente, con el fin de caracterizar las propiedades de los equilibrios de Nash puros en estas. El estudio se concentró en dos propiedades de interés, a saber: el número promedio de individuos que delinquen en la red (19), o criminalidad promedio, y la entropía de equilibrios de Nash puros (20) que corresponde al logaritmo del número de estos. En particular, se estudió como varían dichas propiedades con los parámetros del modelo.
Si bien hay evidencias de que las redes oscuras, como las redes delincuenciales tienen la topología de una red libre de escala [18], con el objeto de facilitar este primer análisis se asumió que la topología de las redes delincuenciales en consideración es la de un grafo aleatorio o Erdós-Rúnyi. Este tipo de grafos se genera primero seleccionando un conjunto de N nodos y luego uniendo pares de nodos al azar hasta completar M vínculos. La conectividad promedio de estos grafos, es decir el número de vínculos que en promedio tiene un nodo escogido al azar es simplemente C = 2M/N. Así pues, se generaron grafos con N nodos y M vínculos y se resolvieron las ecuaciones de la cavidad correspondientes con el fin de estimar el nivel de criminalidad promedio (19) y el logaritmo del número de equilibrios de Nash (20), o entropía, para diversos valores de los parámetros. En todos los casos se escogió N = 100 y M = 250, y por lo tanto C = 5.
En general se observó que los resultados muestran una gran granularidad, probablemente debido a la presencia de las funciones máximo en la función de utilidad y al carácter discreto de las variables involucradas. Este es un punto importante que se debe estudiar en futuras investigaciones.
Las Figuras 3(a) y 3(b) muestran los resultados obtenidos con πr0 = 0.5 y φ = 0.5 y el parámetro δ variando en [0.5,3.5]. Análogamente, las Figuras 3(c) y 3(d) corresponden a φ = 3.8 y 0 = 0.3, y con π0 variando en [0.1, 0.9]. Por último, las Figuras 3(e) y 3(f) se obtuvieron con δ = 1.7 y π0 = 0.5, con φ variando en [0.15,1]. Note que en todas estas figuras se reportan cantidades normalizadas por el número de individuos en la red, es decir (x)/N y S/N.
En la Figusra 3(a) se puede observar que la criminalidad promedio es alta para valores pequeños de δ, manteniéndose casi constante para valores entre 0.5 y 1. Para δ = 1 la criminalidad promedio disminuye considerablemente y a partir de allí manifiesta una leve disminución hasta estabilizarse en aproximadamente 0.55 cuando δ ≥ 3. Dado que el parámetro δ mide el nivel de competencia por los recursos limitados, se puede considerar que esta disminución de la criminalidad promedio con el aumento de δ es un indicador de que las ganancias disminuyen en la medida en que más individuos delinquen, tal y como se espera de la definición del modelo. La Figura 3(b) muestra que la entropía se mantiene igual a cero para valores de delta entre 0.5 y 1, lo cual indica un número sub-exponencial de equilibrios de Nash. Cuando δ = 1 la entropía manifiesta un crecimiento abrupto y a partir de allí manifiesta un crecimiento lento hasta alcanzar un valor de 0.6 cuando δ se aproxima a 3.5. Un valor positivo equivale a un número de equilibrios de Nash que crece exponencialmente con el número de individuos en la red.
Con respecto a una entropía positiva podrían ocurrir dos situaciones: En primer lugar, al existir tantos equilibrios de Nash puede resultar relativamente fácil para los individuos en la red encontrar uno y en ese sentido la actividad criminal en la red podría interpretarse como el resultado de un comportamiento "racional.en el sentido de la teoría de juegos. Por otra parte, al tener tantos caminos conducentes a equilibrios de Nash podrían confundirse y no encontrar ninguno, dado que se requeriría un esfuerzo de coordinación adicional para converger a un equilibrio específico de los tantos disponibles. Un mejor entendimiento requeriría de la introducción de dinámicas de aprendizaje [26] y / o de nociones más refinadas de equilibrio, lo cual se deja para estudios posteriores.
Con respecto al parámetro π0 es importante anotar que los cambios observados son minúsculos, por lo que podría considerarse que no hay variaciones con este. La Figura 3(c) muestra que la criminalidad promedio experimenta una leve disminución, casi que escalonada, en la medida que π0 aumenta tornándose constante cuando π0 alcanza un valor próximo a 0.66. Esto deja ver que aumentando la intensidad de la sanción aplicada, representada por π0, puede en principio disminuirse la criminalidad promedio pero dicha disminución es prácticamente imperceptible. Así mismo, en la Figura 3(d) puede verse que el comportamiento de la entropía es similar al de la criminalidad promedio puesto que también disminuye cuando π0 aumenta y también logra estabilizarse cuando π0 alcanza un valor próximo a 0.4. Esto indica que aumentando la sanción promedio se entorpece, aunque mínimamente, la consecución de equilibrios de Nash, y entonces la red criminal se ve afectada en forma negativa.
Por otra parte, la Figura 3(e) indica que la criminalidad promedio crece en forma escalonada en la medida que φ también aumenta variando entre 0.3 y 0.65, aproximadamente. Los cambios en la criminalidad promedio se dan de forma notoria cuando φ pasa de 0.34 a 0.35 y un poco menos cuando φ pasa de 0.5 a 0.51.
Estos resultados sugieren que los valores de φ deben mantenerse bajos porque este parámetro indirectamente regula la sanción que un delincuente particular pueda recibir. En otras palabras, entre más grande sea φ menor tiende a ser la probabilidad de que un delincuente en particular sea capturado. Este parámetro podría forzarse a tomar valores suficientemente bajos tratando de intervenir la intensidad de las interacciones de un individuo con sus compañeros directos, lo que podría quizá lograrse mediante campañas publicitarias o educativas.
Por último, en la Figura 3(f) se observa que la entropía aumenta con el parámetro φ también aumenta tomando valores entre 0.1 y 0.55, aproximadamente. Este aumento escalonado de la entropía se da de forma notoria cuando φ pasa de 0.34 a 0.35 y un poco menos cuando φ pasa de 0.5 a 0.51. También se puede notar una pequeña disminución en los valores de la entropía cuando φ asume valores próximos a 0.2.
7. Conclusiones
En este trabajo se definió un modelo de redes delincuenciales basado en la teoría de juegos [27] y se exploraron algunas propiedades estadísticas de sus equilibrios de Nash. Se mostró como se puede formular el problema de encontrar equilibrios de Nash como un problema de satisfacción de restricciones y cómo se puede mapear formalmente dicho problema a un sistema físico ficticio equivalente, con el fin de explotar los métodos matemáticos y computacionales de la mecánica estadística para su estudio. Se presentó también introducción a este tema, cuya formalización matemática rigurosa es un área muy activa de investigación en la actualidad. Uno de los métodos principales aquí estudiados fue el método de la cavidad el cual da lugar a un algoritmo de paso de mensajes que permite resolver el problema en consideración de manera eficiente, aunque aproximada.
A partir de estas técnicas se exploró el modelo de redes delincuenciales aquí propuesto en función de sus parámetros. Más específicamente, se generaron computacionalmente redes con la topología de grafos aleatorios o de Erdós-Rúenyi. Se estudió la variación de la criminalidad promedio y del número de equilibrios de Nash, o mejor de su logaritmo o entropía, en función de tres parámetros que definen el modelo. Estos parámetros se relacionan, respectivamente, con la intensidad de competencia global (δ), la colaboración local entre individuos en la red (φ), y la intensidad de las sanciones impuestas (π0). Se observó que la variación con π0, dentro del rango estudiado, es prácticamente irrelevante, mientras que la variación con δ y φ es mucho más notoria. Los resultados de esta investigación sugieren que para atacar este tipo de redes delincuenciales puede ser más efectivo utilizar estrategias que busquen modificar la intensidad de interacción de los individuos en la red, en vez de aumentar la intensidad de las sanciones impuestas. Descubrimos que mantener bajos los valores de la intensidad de competencia global (δ) implica una disminución de la criminalidad promedio y un número bajo de equilibrios de Nash, luego, una estrategia que permita que la ganancia bruta de cada individuo se vea disminuida ayudara a debilitar a estas redes delincuenciales. Esta puede ser haciendo menos rentable la actividad delincuencial.
Referencias
[1] D. Lazer, A. Pentland, L. Adamic, S. Aral, A.-L. Barabási, D. Brewer, N. Christakis, N. Contractor, J. Fowler, M. Gutmann, T. Jebara, G. King, M. Macy, D. Roy, and M. Van Alstyne, Science 323, 721 (2009).
[2] V. Backaitis, "Data is the new oil," (CMS Wire, 2012).
[3] M. O. Jackson and Y. Zenou, Games on Networks, Tech. Rep. (Department of Economics, Stanford University, 2014).
[4] D. Helbing and A. F. Carbone, Eur. Phys. J. Special Topics (Special Issue) 214, 1 (2012).
[5] J. Giles, Nature News 488, 448 (2012).
[6] P. Rotella, "Is data the new oil?" (Forbes, 2012).
[7] A. F. Tenorio-Villalón and A. M. Martin-Caraballo, B. Mat. 22, 77 (2015).
[8] C. Ballester, Y. Zenou, and A. Calvo-Armengol, J. Eur. Econ. Assoc. 8, 34 (2010).
[9] T. A. Sarmiento Bahoque, J. F. Cantillo Palacio, J. E. Realpe Gomez, and J. A. Montoya Martínez, Ing. Cienc. 12,83 (2016).
[10] M. Mézard, G. Parisi, and R. Zecchina, Science 297, 812 (2002).
[11] M. Talagrand, Spin Glasses: A Challenge for Mathematicians - Cavity and Mean Field Models (Springer Science & Business Media, 2003).
[12] M. Talagrand, Mean Field Models for Spin Glasses - Volume I: Basic Examples (Springer Science & Business Media, 2011).
[13] F. Guerra and F. L. Toninelli, Commun. Math. Phys. 230, 71 (2002).
[14] F. Guerra, Commun. Math. Phys. 233, 1 (2003).
[15] M. Mézard and G. Parisi, Information, Physics, and Computation (Oxford University press, 2009).
[16] M. Mézard and G. Parisi, Eur. Phys. J B 20, 217 (2001).
[17] M. Múezard and G. Parisi, J. Stat. Phys. 111, 1 (2003).
[18] J. Xu and H. Chen, Commun. ACM 51, 58 (2008).
[19] S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi, Science 220, 671 (1983).
[20] A. Ramezanpour, J. Realpe-Gomez, and R. Zecchina, Eur. Phys. J B 81, 327 (2011).
[21] H. A. Bethe, P. Roy. Soc. Lond. A Mat. 150, 552 (1935).
[22] R. Peierls, P. Roy. Soc. Lond. A Mat. 154, 207 (1936).
[23] F. R. Kschischang, B. J. Frey, and H. A. Loeliger, IEEE T. Inform. Theory 47, 498 (2001).
[24] F. Altarelli, R. Monasson, G. Semerjian, and F. Zamponi, CoRR abs/0802.1829 (2008).
[25] J. von Neumann, O. Morgenstern, H. Kuhn, and A. Rubinstein, Theory of Games and Economic Behavior, Princeton Classic Editions (Princeton University Press, 2007).
[26] J. Realpe-Gomez, B. Szczesny, L. DallAsta, and T. Galla, J. Stat. Mech.-Theory E. 2012, P10022 (2012).
[27] M. Jackson, Social and Economic Networks, Princeton University Press (Princeton University Press, 2010).