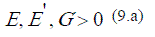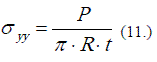ANISOTROPÍA MECÁNICA DEL NEIS DE LA CASA DE MÁQUINAS DE LA HIDROELÉCTRICA PORCE III

Se presenta el proceso y los resultados obtenidos de diferentes ensayos de laboratorio efectuados sobre la roca intacta de un neis proveniente del Proyecto Hidroeléctrico Porce III, en Colombia, con el fin de determinar su grado de anisotropía de deformación y de resistencia a la ruptura. Se observó que el neis en estudio es una roca tenaz, frágil, con bajo grado de anisotropía, adecuado para modelarse como un comportamiento elástico de isotropía transversal y por medio del criterio de ruptura de Drucker-Prager.

MECHANICAL ANISOTROPY OF THE GNEIS AT THE PORCE III HYDROELECTRIC POWERHOUSE

LUDGER SUAREZBURGOA
Departamento de Engenharia Civil e Ambiental/FT, Universidade de Brasília, Brasil (Estudiante Doctorado)
lsuarezburgoa@unb.br

ÁLVARO CASTRO CAICEDO
Facultad de Minas, Universidad Nacional de Colombia Sede Medellín, Colombia (Profesor Asistente)
lsuarezburgoa@unb.br

ANDRÉ PACHECO DE ASSIS
Departamento de Engenharia Civil e Ambiental/FT, Universidade de Brasília, Brasil (Profesor Titular)
lsuarezburgoa@unb.br

Recibido para evaluación: 27 de Septiembre de 2009 / Aceptación: 13 de Mayo de 2010 / Recibida versión final: 24 de Mayo de 2010

RESUMEN

Se presenta el proceso y los resultados obtenidos de diferentes ensayos de laboratorio efectuados sobre la roca intacta de un neis proveniente del Proyecto Hidroeléctrico Porce III, en Colombia, con el fin de determinar su grado de anisotropía de deformación y de resistencia a la ruptura. Se observó que el neis en estudio es una roca tenaz, frágil, con bajo grado de anisotropía, adecuado para modelarse como un comportamiento elástico de isotropía transversal y por medio del criterio de ruptura de Drucker-Prager.

PALABRAS CLAVES: Neis; isotropía transversal; roca intacta; Porce III; Geomecánica, Antioquia; Colombia.

ABSTRACT

In this work is presented the results of the different laboratory tests carried out on gneissic intact rock of the Porce III Hydroelectric Project, Colombia, in order to determine the degree of deformation and failure strength anisotropy under stress. This study concludes that the gneiss is a sound, brittle, of high strength and low grade anisotropic rock, and can be well modeled by a transverse isotropic linear elastic behavior under the Drucker-Prager failure criterion.

KEY WORDS: Gneiss; transverse isotropy; intact rock; Porce III; Colombia;

1. INTRODUCCIÓN

Conocer el grado de anisotropía de las rocas es importante para comprender su comportamiento ante la aplicación de cargas, y su omisión puede, dependiendo del caso, ocasionar errores en la estimación del desempeño de la roca (Tsidzi, 1986), hecho que para el caso de una caverna de generación hidroeléctrica es de alta importancia. El presente artículo muestra los estudios sobre la roca intacta del neis constituyente en mayor medida del macizo rocoso en la caverna de generación de la Hidroeléctrica Porce III con el fin de caracterizar el grado de anisotropía mecánica.

2. ANISOTROPÍA DE ROCAS

El término anisotropía se refiere a las diferencias de las magnitudes de las propiedades físicas cuando son observadas en distintas direcciones de un cuerpo. Estas propiedades pueden ser de resistencia a esfuerzos, de deformación (e.g. módulo de deformación elástica), hidráulicas (e.g. permeabilidad), o de frecuencia de fracturamiento.

El grado de anisotropía de las rocas puede observarse a través de tres formas de estudio:

a) encontrando algunos índices previamente definidos, llamados índices de anisotropía, y compararlos con los rangos de su correspondiente clasificación preestablecida.
b) obteniendo algunos o todos los parámetros índices de la roca en diferentes orientaciones de los planos de anisotropía.
c) obteniendo parámetros de modelos constitutivos anisotrópicos del material.

(a) Índices de anisotropía

La diferencia entre dos valores de una misma propiedad en diferentes direcciones, generalmente perpendicular y paralela a un plano de simetría o plano de anisotropía, se cuantifica a través de una razón denominada Índice de Anisotropía.

El valor numérico del Índice de Anisotropía varía para una misma roca en función de los ensayos a partir de los cuales se determina. El Índice de Anisotropía se puede calcular con base en técnicas de descripción de la microfábrica (e.g. microscopía óptica, microscopía electrónica, difractrometría de rayos X) (Tsidzi, 1986), propiedades consideradas índice (e.g. resistencia bajo carga puntual, velocidad de propagación de ondas ultrasónicas, y ondas P) (ISRM, 1981; Saroglou & Tsiambaos, 2006, 2007), valores de resistencia (e.g. resistencia a la compresión ó tracción) (Ramamurthy, 1993) y valores de deformación (e.g. módulos de deformación elástica) (Worotnicki, 1993; Nasseri et al., 2003).

Tsidzi (1986) planteó la siguiente ecuación para determinar el índice de foliación (F) de la roca, que en cierto modo describe el grado de anisotropía de la misma (Ec. 1); donde Mi representa el porcentaje modal de los minerales cuyos valores de Factor de Forma (Si) fueron analizados. El Si de un mineral es la relación de la máxima con la mínima dimensión del mineral en el plano de análisis.

A partir del índice de foliación se puede clasificar a la roca según su grado de foliación (Tabla 1). Alternativamente, F puede hallarse a partir de conocer la relación entre la proporción de minerales planos respecto a la proporción de minerales prismáticos (M), empleando la ecuación de correlación propuesta por Tsidzi (1986) (Ec. 2).

Tabla 1. Clasificación de la roca de acuerdo al índice de foliación (Tsidzi, 1986).

La Sociedad Internacional de Mecánica de Rocas, ISRM, propuso el índice de anisotropía a partir de resultados de índices de carga puntual simple (Ec. 1), donde Is(50)? y Is(50)// son los índices de carga puntual ensayados y/o corregidos a un tamaño de cuerpo de prueba de 50 mm de diámetro para una carga puntual aplicada perpendicular y paralelo a los planos de simetría, respectivamente; sin tomar en cuenta si el ensayo es axial o diametral. La ISRM (1981) clasificó la anisotropía de las rocas de acuerdo a ese índice (Tabla 2).

Tabla 2. Clasificación de la anisotropía de acuerdo al índice de carga puntual (ISRM, 1981).

Saroglou & Tsiambaos (2006) proponen una nueva clasificación en función de resultados de ensayos de carga puntual (Ec. 4), donde Ids(50)? y Ids(50)// son los índices de carga puntual ensayados/ corregidos a un tamaño de núcleo de 50 mm de diámetro para una carga puntual aplicada necesariamente en forma diametral a los cuerpos de prueba, y que deben tener planos de simetría perpendicular y paralelo a la dirección de carga, respectivamente. La tabla 3 muestra la clasificación propuesta por estos autores.

Tabla 3. Clasificación de la anisotropía de acuerdo al índice de carga puntual diametral (Saroglou & Tsiambaos, 2006).

Saroglou & Tsiambaos (2007) determinaron que el índice de anisotropía a partir de los ensayos de carga puntual (Ia50), según las recomendaciones de la ISRM, es ineficiente; mientras que el índice de anisotropía a partir de los ensayos de carga puntual diametral tiene resultados más cercanos a los obtenidos por los índices de anisotropía de resistencia a compresión uniaxial. Estos autores también encontraron correlaciones de estos dos índices.
A partir de la velocidad de propagación de ondas ultrasónicas en la roca intacta Tsidzi (1997) propuso clasificar la anisotropía de las rocas de acuerdo a la relación de la ecuación 5, son la velocidad de propagación de ondas ultrasónicas máxima, mínima y promedio, respectivamente. La clasificación de acuerdo a este índice se muestra en la Tabla 4.

Tabla 4. Clasificación de la anisotropía de acuerdo a la velocidad de propagación de ondas ultrasónicas (Tsidzi, 1997).

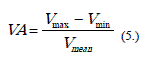
Saroglou & Tsiambaos (2007) proponen otra clasificación en función a la velocidad de propagación de ondas P (ondas longitudinales) según la ecuación 6, donde 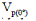es la máxima velocidad de propagación de la onda P paralela a los planos de simetría y es mínima velocidad de propagación de la onda perpendicular a los planos de simetría. La tabla 5 muestra esta clasificación.

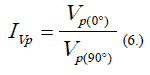
Tabla 5. Clasificación del grado de anisotropía de las rocas (Saroglou & Tsiambaos, 2006).

Estudios para determinar la anisotropía a partir de parámetros de resistencia fueron hechos por Ramamurthy (1993). El índice de anisotropía a partir de este parámetro se define en la siguiente ecuación (Ec. 7), donde son los valores de la resistencia a compresión uniaxial de la roca intacta para un ángulo de inclinación conjugado del plano de simetría respecto el plano donde actúa el esfuerzo desviador y para aquel ángulo w que brinde el mínimo valor de resistencia a compresión uniaxial, respectivamente.

Basados en la determinación de los índices de anisotropía en varias rocas sedimentarias y metamórficas, Ramamurthy (1993) propuso la siguiente clasificación del grado de anisotropía de la roca (Tabla 6).

Tabla 6. Clasificación del grado de anisotropía de las rocas de acuerdo al índice de anisotropía en resistencia a la compresión (Ramamurthy, 1993).

Estudios para determinar la anisotropía de los parámetros de deformación fueron hechos por Worotnicki (1993) y Nasseri et al. (2003). La relación del máximo módulo de elasticidad con el mínimo se ha planteado como un índice de anisotropía

De los estudios de Worotnicki (1993) se encontró que las rocas cuarzofeldespáticas y las rocas básicas muestran bajos a moderados grados de anisotropía, con relaciones de anisotropía menores a 1,3 para los Módulos Elásticos. En carbón este valor se observó que no excede de 1,7, y en las rocas pelíticas el máximo valor encontrado fue de seis y en el mayor de los casos un valor menor a cuatro. De acuerdo con estos valores se propone la siguiente clasificación (Tabla 7).

Tabla 7. Clasificación del grado de anisotropía de las rocas (de Worotnicki, 1993)

(b) Var iación de par ámetros índice en diferentes or ientaciones de los planos de anisotropía

Otra forma de caracterizar la anisotropía de la roca es a través de la determinación de la variación de diversos parámetros índice (e.g. resistencia a compresión uniaxial, velocidad de propagación de ondas sónicas, parámetros de envolventes de falla) respecto al ángulo de inclinación del plano de simetría y la dirección del ensayo.
El grado de anisotropía de algunas roca estudiadas bajo esta forma se encuentran por ejemplo en Donath (1964), Chenevert & Gatline (1965), McLamore & Gray (1967), Hoek (1968), Attewell & Sandford (1974) y Ramamurthy et al. (1988).

(c) Obtención de par ámetr os de modelos constitutivos del material

Finalmente, el grado de anisotropía se evalúa si para la misma roca se logran determinar los parámetros de algún modelo constitutivo ortotrópico.
En el presente estudio, para el caso del Neis, se escoge el modelo de isotropía transversal linealmente elástico en un medio continuo. Este modelo de isotropía transversal implica que en cada punto de la roca existe un eje de simetría de rotación, el eje axisimétrico, y que la roca tiene propiedades isotrópicas elásticas en el plano normal a ese eje. El plano se denomina plano de isotropía transversal. Para la completa descripción mecánica de una roca de isotropía transversal se necesitan cinco constantes independientes elásticas, a saber: E, el módulo de Young en el plano de isotropía transversal; E', el módulo de Young en el plano normal al plano de isotropía transversal; , la relación de Poisson que caracteriza la respuesta a la deformación lateral en el plano de simetría transversal a un esfuerzo que actúa paralelo al mismo; ', la relación de Poisson que caracteriza la respuesta a la deformación lateral en el plano de simetría transversal a un esfuerzo que actúa normal al mismo; y G', el módulo de cortante en el plano normal al plano de isotropía transversal.

Para estos parámetros del modelo de isotropía transversal deben cumplirse las restricciones de la energía de deformación, presentadas en las Ecuaciones 9.

Las constantes elásticas anisotrópicas son en su mayoría determinadas de los resultados de ensayos estáticos, asumiendo un comportamiento lineal elástico, tales como: resistencia a compresión uniaxial (UCS), resistencia a compresión triaxial axisimétrica (TCS), resistencia a compresión triaxial verdadera, resistencia a tracción indirecta (ensayo brasilero) (ITT), ensayos de torsión y flexión. Para todos estos ensayos se deben ensayar especímenes de prueba cortados con diferentes ángulos respecto a los planos de simetría, y se deben instalar galgas de deformación para medir las deformaciones unitarias.

El ensayo más simple y económico dentro de éstos es el de resistencia a la tracción indirecta asumiendo un comportamiento anisotrópico transversal, que es el realizado en este trabajo. En este caso las galgas de deformación son instaladas en el centro del plano directriz formando una roseta con ejes axiales a 45° (Figura 1). Soluciones analíticas cerradas se han deducido para relacionar las constantes de una roca anisotrópica sometida a una carga diametral con las deformaciones en el centro de la misma, donde se asume que los esfuerzos concentrados en el centro de un disco de roca anisotrópica son los mismos que en una roca isotrópica (Pinto, 1979).

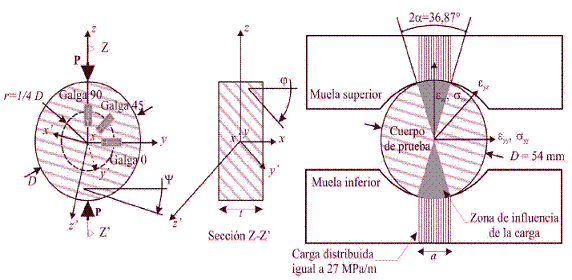
Figura 1. Disposición de las galgas de deformación y nomenclatura de las ecuaciones de esfuerzo y deformación para el ensayo de tracción indirecta.

Hondros (1959) ha analizado la distribución de esfuerzos en el ensayo de tracción indirecta para el caso de un disco delgado cargado a una presión uniforme, aplicada radialmente sobre una pequeña franja de la circunferencia en cada extremo del diámetro. Los esfuerzos de interés, aquellos que actúan en puntos a lo largo del diámetro vertical ZZ' en la Figura 1, están dados por las siguientes ecuaciones, para el esfuerzo tangencial y el esfuerzo radial 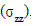, respectivamente (Ecuación. 10); donde P es la fuerza aplicada, a es el ancho proyectado de la corona del sector cargado, t es el espesor del disco, s es la mitad del ángulo del sector cargado, r es la distancia radial de un punto desde el centro del disco, y R es el radio del disco. Los esfuerzos con direcciones coincidentes con los ejes adoptados en estas ecuaciones son positivos. En el centro del disco la expresión de esfuerzo tangencial se reduce a la expresión de la Ecuación 11. Esta expresión se usa para calcular la resistencia a la tracción del material y es válida para a < R / 5.

Los valores de (en radianes) dependen de la cuña de carga del equipo de tracción indirecta que se emplea, generalmente se asume entre 1/12 (4,77°), cuando no se usa material deformable entre el cabezote de apoyo y el cuerpo de prueba a 1/3 (19,10°), si se usa dicho material. Para hallar las constantes elásticas de la isotropía transversal se debe resolver la siguiente ecuación matricial (Ec. 12), donde {;e} y {;s} son los vectores de deformaciones unitarias y de esfuerzos en el plano x, y, z respectivamente.

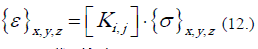
es una matriz de 6 x 6 con términos en función de las variables ; en el plano de simetría definido en el espacio x, y, z por los ángulos de inclinación aparentes F (Figura 1). La relación de G' con E, E' y n' se obtiene de la Ecuación 13, y las variables de inclinación aparentes son conocidas. De este modo las incógnitas son finalmente cinco.

Las expresiones de cada término de la matriz [K i,j ] están desarrolladas en Nunes (2002). Para el ensayo de tracción indirecta las variables 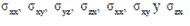son iguales a cero en el centro de la muestra. Las deformaciones en   se obtienen de las lecturas de las galgas de deformación para el nivel de esfuerzo 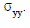. Los esfuerzos son iguales a las expresiones de la Ecuación 10, evaluadas en el centro de la muestra, respectivamente.

El procedimiento de solución es iterativo, siguiendo un orden específico: primero se resuelven las ecuaciones con los valores obtenidos de los ensayos hechos sobre especímenes de prueba con una inclinación de 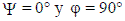. Estas iteraciones darán valores de E y n. Luego se resuelven las ecuaciones con los datos de los ensayos con ángulos de inclinación , cuyos resultados darán los valores de E' y n'; finalmente se resuelven los especímenes de prueba con los ángulos diferentes de 0° y/o 90°, que dará el valor de G'. Durante todo el proceso iterativo se deben verificar que se cumplan las restricciones de energía citadas en las ecuaciones 9.

3. EL NEIS DE LAS CAVERNAS DE GENERACIÓN DE PORCE III

La roca intacta motivo de este estudio proviene del macizo rocoso que alberga la Casa de Máquinas de la Hidroeléctrica Porce III (CMP3), localizada al noreste del Departamento de Antioquia, en jurisdicción del Municipio de Amalfi; región que concierne al flanco este de la Cordillera Central de los Andes (Figura 2). El punto central de la CMP3 se encuentra en las coordenadas 1 267 984 N, 890 915 E en el sistema USR con origen en Bogotá.

Figura 2. Ubicación del sitio de la roca estudiada (Sitio CSCP3), modificado de (EE.PP.M E.S.P, 2005)

De forma general, el neis es una roca masiva, tenaz, compacta, bandeada, incipiente e irregularmente foliada. Está compuesta por bandas grises micáceas de textura lepidoblástica, especialmente compuesta de biotitas y moscovitas, y de bandas blancas lechosas compuestas especialmente por plagioclasa, feldespato potásico y cuarzo (Suarez-Burgoa, 2008). Las propiedades índices de la roca intacta se muestran en la Tabla 8. Los parámetros de deformación promedio de la roca intacta, asumiendo ésta como isotrópica y linealmente elástica, para el módulo elástico a 50% de la sci fueron de E 50 = 64 GPa y relación de Poisson v = 0,20. Mecánicamente el material de roca es frágil y obedece la envolvente de falla Drucker-Prager (Figura 3).

Tabla 8. Propiedades principales del neis intacto (SuarezBurgoa, 2008).


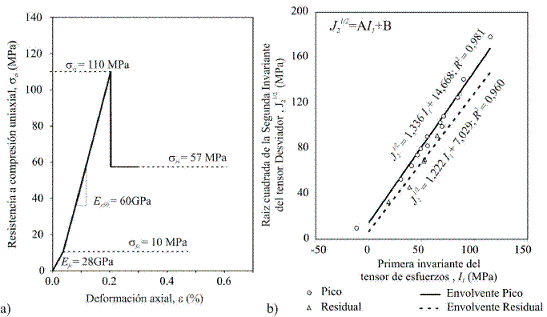
Figura 3. Comportamiento mecánico de la roca intacta (SuarezBurgoa, 2008): a) Modelo esfuerzo deformación lineal elástico frágil bajo compresión uniaxial  ( βw = 0° ), b) Envolvente de falla DruckerPrager ( βw = 45° ).

4. MÉTODO EXPERIMENTAL

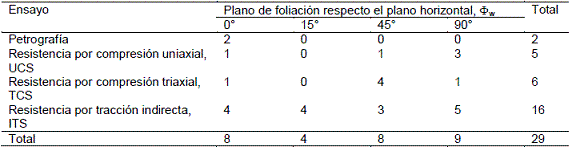
Para especímenes de prueba de roca intacta no porosa se considera que las presiones de poros no tienen efectos en los resultados de resistencia  ensayados bajo velocidades de deformación estándares. De este modo, en esta investigación las condiciones de humedad de las muestras ensayadas fueron las del ambiente. Las muestras fueron extraídas de una profundidad promedio de 260 m bajo el nivel del terreno. La Tabla 9 resume las cantidades de los especímenes de prueba preparados para los ensayos especializados.

Tabla 9. Cantidades de especímenes de prueba preparados para ensayos.

Micro-petrografía

El objeto del análisis de micro-petrografía (Figura 4) fue el de diferenciar los tipos de minerales presentes con fines de clasificación petrográfica, de analizar la distribución de tamaño de minerales y determinar la orientación de los minerales y las micro-fisuras. Se puede considerar el neis como de composición homogénea en muestras de mano, con tamaños de minerales en un rango probable de 0,18 mm a 1,06 mm (promedio de 0.33 mm), un mínimo de 0,05 mm y un máximo de 4 mm.

Figura 4. Microfotografía de la sección delgada PTR02(A): a) Luz normal (Nicoles paralelos), b) Luz transversal polarizada (Nicoles cruzados).

Ensayo de velocidad sónica

El método de ensayo de velocidad sónica empleado fue el de Transmisión de Pulsos correspondiente al método sugerido por la ISRM (Rummel & Van Heerden, 1978). La velocidad de propagación sónica tuvo un valor medio de 4 489 m/s.

Ensayos de tracción indirecta

En este ensayo se aplicó compresión en una tasa de carga de 0,9 MPa s ­¹, según las recomendaciones de la ISRM (1978). Trece de las dieciséis muestras ensayadas fallaron formando una ruptura diametral vertical. Si se considera que la resistencia por tracción indirecta no es influenciada por el plano de foliación (i.e. material homogéneo isotrópico) la resistencia por tracción de la roca intacta tiene un valor medio de -15,2 MPa.

Ensayos de resistencia por compresión uniaxial

El ensayo UCS se ha efectuado bajo las normas de la ISRM (Brown, 1981), ASTM D2938-95 y ASTM D3148-84. El ensayo fue conducido bajo control de velocidad de deformación radial, correspondiente a una tasa de carga de 0,8 MPa s ­¹

Ensayos de resistencia por compresión triaxial

Las tres presiones de confinamiento para los ensayos de resistencia por compresión triaxial (TCS) fueron definidas con base en el rango de las presiones extremas presentes en el macizo rocoso del sitio de estudio, que comprenden desde cero MPa hasta catorce MPa; y las recomendaciones de Sari & Karpuz (2006). De acuerdo con estos criterios, las tres presiones de confinamiento escogidas fueron de 3, 8 y 12 MPa. El procedimiento para obtener la envolvente de falla y las relaciones esfuerzo deformación fue el Ensayo Escalonado (i.e. ensayo de múltiples estados de falla) (Kovari et al., 1983). Consiste en aplicar una carga al espécimen de prueba bajo esfuerzo isotrópico hasta alcanzar la primera presión de confinamiento (i.e. 3 MPa), luego la carga axial se incrementa manteniendo la presión de confinamiento constante hasta llegar a la resistencia pico, que se observa en la curva esfuerzo axial - deformación axial. Sin cargar de forma elevada la roca en el nivel de pico, la presión de confinamiento se incrementa a la correspondiente presión intermedia. (i.e. 8 MPa). Después de ello, la carga axial es nuevamente incrementada hasta observar un nuevo pico para aquella presión. Finalmente, por tercera vez se incrementa la presión de confinamiento hasta el máximo valor de presión (i.e. 12 MPa) y la carga axial se incrementa hasta observar la curva pico y la curva post rotura hasta encontrar el valor residual. Para estos ensayos se usó una tasa de deformación diametral de para el rango elástico hasta antes del 70% del primer pico y para la parte final de la curva de post rotura. Para las demás partes de la curva se empleó una tasa de deformación diametral de . Debido a las exigencias de este procedimiento, se empleó una máquina servo controlada.

Medidas de deformaciones en el ensayo ITT

Adicionalmente al procedimiento de ensayo estándar de tracción indirecta descrito, en cada espécimen de los 16 ensayados se han medido las deformaciones a través de tres galgas de deformación axiales (i.e. ExcelSensores referencia PA06250BA-120-L) adheridas en forma de una roseta con 0º, 45º y 90º con el objetivo de obtener los parámetros del comportamiento esfuerzo-deformación. Las galgas fueron orientadas una paralela a la dirección de carga, la segunda perpendicular a la primera y la tercera a una dirección de 45° respecto con las dos anteriores.

Se ha usado un valor de 0,32 rad (18,4°) para la variable del modelo (ver Figura 2 y Ecuación 2). El valor medio del radio de los especímenes de prueba fue de R = 26,8 mm (i.e. diámetro D = 54,0 mm) y el espesor de t = 22,2 mm. Los esfuerzos fueron calculados para el centro de la muestra (i.e. para un radio r = 0 mm) según las ecuaciones 11 y Ecuación12.

Las deformaciones unitarias tomadas para los cálculos fueron para un esfuerzo promedio de tracción de δyy = 5,52 ± 1,5 SSyy  (MPa), siendo la desviación estándar (SSyy) igual a 0,06 MPa.

La Figura 5 muestra las medidas de las galgas de deformación obtenidas para la muestra A90ITT03 (i.e. ángulo βw = 0°). Con un círculo se observan los puntos donde se extrajeron los datos de las deformaciones para el nivel de esfuerzos mencionado. De los 16 especímenes de prueba ensayados se escogieron 13 para el cálculo de las constantes, ya que los otros tres especímenes de prueba no fallaron por el eje central del cilindro como la norma exige para validar el ensayo.

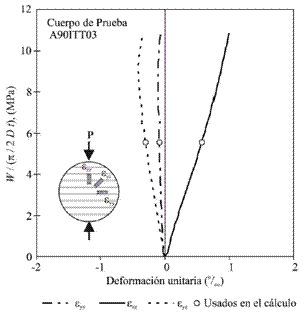
Figura 5. Medidas de deformaciones con las galgas de deformación en la muestra A90ITT03

5. RESULTADOS

La Tabla 10 muestra los valores del Índice de Anisotropía de acuerdo con los criterios de clasificación planteados por los diferentes autores descritos en la sección dos del presente artículo: "Anisotropía de rocas". En esta tabla, como cada fila corresponde a un distinto criterio de clasificación con diferentes rangos según lo planteado por cada autor, los valores numéricos no son mutuamente comparables, sin embargo por la clasificación que cada uno genera, tercera columna, se observa y concluye que el neis de este estudio es levemente anisotrópico.

Tabla 10. Valores de índices de anisotropía en el Neis

La variación de la resistencia a la tracción indirecta respecto el ángulo ψ se muestran en la Figura 6a. Vea esta anterior figura, o también la Figura 1, para conocer cómo fueron definidos los ángulos  ψ y Ψ en la muestra de forma de moneda.

Por otro lado, la variación de la resistencia a la compresión uniaxial respecto al ángulo b w del neis en estudio se muestra en la Figura 6b. En este caso el ángulo b w es el ángulo de inclinación conjugado (Φ w ) del plano de simetría respecto el plano donde actúa el esfuerzo desviador en muestras de forma de cilindrorecto, tal como se muestra en el esquema de la cuerpo de prueba de la Figura 6b.

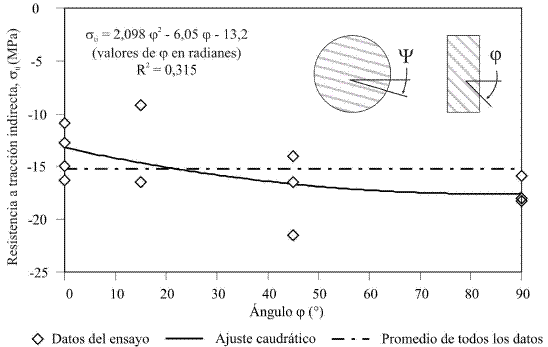
Figura 6. Variación de la resistencia a la tracción indirecta de la roca intacta con relación a la inclinación del plano de simetría del neis (j) para Ψ = 0°

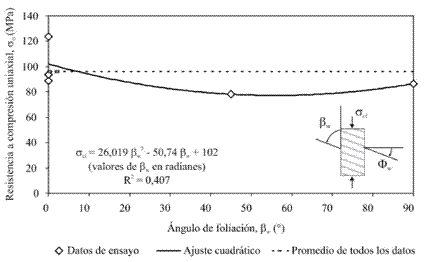
Figura 7. Variación de la resistencia a la compresión uniaxial de la roca intacta con relación al ángulo βw .

Asimismo, se propone la variación de los parámetros de la envolvente de falla Drucker-Prager respecto el ángulo βw (Figura 8).

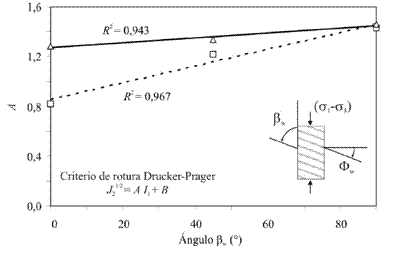
Figura 8. Parámetros de la envolvente de falla Drucker-Prager respecto el ángulo β w  : a) Parámetro A, b) Parámetro B

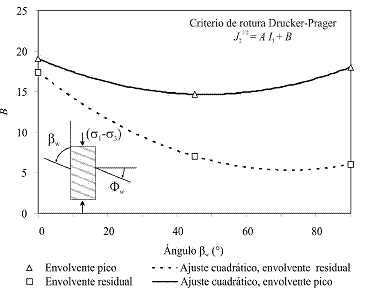
Figura 8. (Continuación). Parámetros de la envolvente de falla Drucker-Prager respecto el ángulo β w : a) Parámetro A, b) Parámetro B

Finalmente, por medio de un proceso de inversión se han obtenido las constantes elásticas de isotropía transversal de la roca en estudio. El error global de la estimación del cálculo fue de 29%, dejando fuera del cálculo las medidas de tres especímenes de prueba: A90ITT02, B00ITT23 y A45ITT17; debido a que incrementaban el error global en gran medida. La Figura 9 compara los valores de las deformaciones axiales medidas con las modeladas, en la dirección y y z. La Tabla 11 muestra los rangos de variación de los valores hallados.

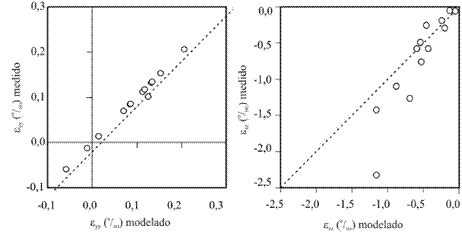
Figura 9. Deformaciones axiales y y z modeladas vs medidas

Tabla 11. Parámetros elásticos de isotropía transversal en el neis estudiado.

6. CONCLUSIONES

El neis estudiado es de bajo grado de anisotropía, tras la evaluación de los resultados de los índices de anisotropía. Según la variación de los parámetros índice estudiados, también se llega a la conclusión de que la roca es levemente anisotrópica. La propiedad índice que refleja en mayor medida la influencia direccional del único plano de isotropía fue la resistencia a tracción indirecta, pues la diferencia entre el máximo y el mínimo en esta propiedad fue de 2,3 MPa, y los valores para los ángulos Ψ = 0° y Ψ = 90° son muy semejantes pudiéndose adoptar un valor medio constante de -15,2 MPa. Saroglou & Tsiambaos (2007) concluyeron que las rocas de alta resistencia a la compresión uniaxial (sci > 100 MPa) generalmente exhiben bajos grados de anisotropía. Esta aseveración también fue observada para este Neis, donde se encontró una relación de anisotropía de 1,3 (i.e. levemente anisotrópica), siendo la resistencia a compresión uniaxial de este material del orden de 90 MPa.

La condición crítica para el esfuerzo uniaxial pico tomando en cuenta la anisotropía del Neis estudiado en esa investigación se presenta para el ángulo β w de 62°. Hakala et al. (2007) encontraron que este valor para un Neis migmatítico micáceo está en un ángulo β w de 47°.

Por otro lado, Amadei (1992) describe que en rocas intactas la relación E / E' varía de 1 a 4, que algunas rocas pueden tener valores menores de 1 pero no se encontró en éstas algún valor menor a 0,7. Han sido encontrados valores para la relación de G / G' entre 1 y 3, para el módulo de Poisson (n) entre 0,1 y 0,35 y para la expresión E / E´ entre 0,1 y 0,7. Para el caso de el Neis estudiado, la relación E / E´ es de 2,5, la relación G / G´ es de 2,4; el valor de la  relación de Poisson (n) es de 0,28 y la expresión E / E´ de 0,7; valores que confirman los rangos propuestos por Amadei (1992).

Finalmente, Bhawani et al. (1998) plantean que el criterio de rotura Mohr-Coulomb debe modificarse para rocas anisotrópicas ya que el esfuerzo principal medio influye en la resistencia de la roca intacta. Este mismo aspecto fue encontrado en esta investigación, donde se encontró que el criterio DruckerPrager, que considera la influencia del esfuerzo principal medio, es el más apropiado para el Neis en estudio, donde los ajustes de los valores ensayados con el criterio planteado tienen un coeficiente de determinación R2 de 0,98 y 0,96, para las condiciones pico y residual respectivamente.

GRADECIMIENTOS

Empresas Públicas de Medellín, ingeniero Gustavo Tamayo, Ingetec S.A., Consorcio Triple-C del Proyecto Hidroeléctrico Porce III, Programa de Pós-Grado en Geotecnia de la Universidad de Brasilia, Brasil. Departamento de Apoyo y Control Técnico, Furnas Centrais Elétricas S.A., Brasil; Dirección Nacional de Investigación (DINAIN), Instituto de Estudios de Infraestructura y Maestría en Ingeniería - Geotecnia de la Universidad Nacional de Colombia, Medellín.
Ludger Suarez-Burgoa agradece a la Cooperación Técnica Belga (BTC) en Bolivia y la Coordinación para el Perfeccionamiento de la Educación Superior de Brasil (Beca nacional: CAPES/CNPq-I IEL).

REFERENCIAS

[01] Amadei, B.; Pan, E., 1992. Gravitational stresses in anisotropic rock masses with inclined strata. Int. J. Rock Mech. & Min. Sci. & Geomech. Abstr., Vol. 29(3), pp. 225-236. Amadei & Savage, 1991

[02] ASTM D2938-95, 1995. Standard Test Method for Unconfined Compressive Strength of Intact Rock Core Specimens. Philadelphia, PA: ASTM International.

[03] ASTM D3148-84, 1984. Test Method for Elastic Module of Intact Rock Core Specimens in Uniaxial Compression. Philadelphia, PA: ASTM International.

[04] Attewell, P.B.; Sandford, M.R., 1974. Intrinsic shear strength of brittle anisotropic rockI: experimental and mechanical interpretation. Int. J Rock Mech. Min. Sci. Vol. 11, pp. 423-430.

[05] Bhawani, S.; Goel, R.K.; Mehrotra, V.K.; Garg, S.K.; Allu, M.R., 1998. Effect of intermediate principal stress on strength of anisotropic rock mass. Tunnelling and Underground space Technology, Vol.13 (1), pp. 71-79.

[06] Brown, E.T., 1981. Rock characterization testing and monitoring: ISRM Suggested Methods. International Society for Rock Mechanics. Oxford: Pergamon Press.

[07] Chenevert, M.E.; Gatline, C., 1965. Mechanical anisotropies of laminated sedimentary rocks. Soc Pet Eng J, pp. 67-77

[08] Deere, D.U.; Patton, F.D., 1971. Slope stability in residual soils. Proc. 4th Panam. Conf. Soil Mech., Puerto Rico 1, 87170.

[09] Donath, F.A., 1964. Strength variation, deformational behaviour of anisotropic rocks. In: Judid, W.R., editor. State of the earth in the earth's crust. New  York: Elsevier, pp. 281-98.

[10] EE.PP.MM. E.S.P., 2005. Construcción de la conducción, central subterránea y obras asociadas, información de geología y geotecnia. Empresas Públicas de Medellín. Vol. 5 (12). Medellín, Colombia.

[11] Hakala, M.; Kuula, H.; Hudson, J.A., 2007. Estimating the transversely isotropic elastic intact rock properties for in situ stress measurements data reduction: A case study of the Olkiluoto mica gneiss, Finland. Int J Rock Mech & Min Sci, Vol.44, pp. 14-46.

[12] Hoek, E., 1968. Brittle failure of rock. In: Stagg, K.G., Zienkiewicz, O.C., editors. Rock mechanics in engineering practice. London: Willey.

[13] Hondros, G.., 1959. Aust. J. appl. Sci. no. 3, pp. 243268.

[14] ISRM, 1978. Suggested methods for determining tensile strength of rock materials. International Society for Rock Mechanics Commission on Standardization of Laboratory and Field tests. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr., Vol. 15, pp. 99-103.

[15] ISRM, 1981. Rock characterization, testing and monitoring, ISRM suggested methods. Pergamon Press, Oxford, U.K.

[16] Kovari, K.; Tisa, A.; Einstein, H.H.; Franklin, J.A., 1983. Suggested methods for determining the strength of rock materials in triaxial compression: revised version. Int J Rock Mech Min Sci Geomech Abstr. Vol.20, pp. 283-290.

[17] Mclamore, R.; Gray, K.E., 1967. The mechanical behaviour of anisotropic sedimentary rocks. Trans Am Soc Mech Eng Ser B, Vol.89, pp. 62-67.

[18] Nasseri, M.H.B.; Rao, K.S.; Ramamurthy, T., 2003. Anisotropic strength and deformational behavior of Himalayan schist. Int. J. Rock. Mech. & Min. Sci. Vol. 40 (1), pp. 3-23.

[19] Nunes, A.L.L.S., 2002. A new method for determination of transverse isotropic orientation and the associated elastic parameters for intact rock. Int. J. rock Mech. Min. Sci., Vol.39, pp. 257-273.

[20] Ramamurthy, T., 1993. Strength, modulus responses of anisotropic rocks. In: Hudson J.A., editor. Compressive rock engineering, Vol. 1. Oxford: Pergamon Press, pp. 313-329.

[21] Ramamurthy, T.; Rao, G.V.; Singh, J., 1988. A strength criterion for anisotropic rocks. Proceedings of the Fifth Australia-Newzeland Conference on Geomechanics, Vol. 1, Sydney, pp. 253-257.

[22] Rummel, F.; Van Heerden, W.L., 1978. Suggested methods for determining sound velocity. Int. J. Rock Mech. & Min. Sci. & Geomech. Abstr., Vol. 15 (2), pp. 53-58.

[23] Sari, M.; Karpuz, C., 2006. Rock variability and establishing confining pressure levels for triaxial tests on rocks. Int. J. of Rock Mech. & Min. Sci., Vol. 43, pp 328-335.

[24] Saroglou, H.; Tsiambaos, G., 2006. Point load strength of anisotropic rocks. Proc. of Eurock 06, European Regional ISRM Conference, Liege, Belgium, pp. 603-607.

[25] Saroglou, H.; Tsiambaos, G., 2007. Classification of anisotropic rocks. 11th Congress of the International Society for Rock Mechanics. In: Ribeiro e Sousa, Otalla, Grossmann, editors. Taylor & Francis Group, London, pp. 191-196.

[26] SuarezBurgoa,L., 2008. Rock mass mechanical behavior assessment at the Porce III underground hydropower central, Colombia, South America. Tesis de Maestría en Ingeniería Geotecnia. Facultad de Minas, Universidad Nacional de Colombia Medellín, p. 350.

[27] Tsidzi, K., 1986. A quantitative petrographic characterization of metamorphic rocks. Bull. Int. Assc. Eng. Geol., N° 33, pp. 312.

[28] Tsidzi, K., 1997. Propagation characteristics of ultrasonic waves in foliated rocks. Bull. Int. Assoc. Eng. Geol., Vol.56, pp. 103-113.

[29] Worotnicki, G. ,1993. CSIRO triaxial stress measurements cell. In: Hudson, J.A., (editor). Comprehensive rock engineering. Vol. 3, pp 329-394. Pergamon, Oxford.