
OPTIMIZACIÓN DEL PAQUETE COMPUTACIONAL PARA EL CÁLCULO DE ESTRUCTURA NÚCLEO-ELECTRÓNICA: APMO
OPTIMIZATION OF SOFTWARE PACKAGE FOR STUDIES OF QUANTUM NUCLEAR EFFECTS: APMO
OTIMIZAÇÃO DO PROGRAMA COMPUTACIONAL PARA O CÁLCULO DA ESTRUTURA ELETRÔNICA E NÃO ELETRÔNICA: APMO
Edwin Posada1, Félix Moneada1, Andrés Reyes1,2
1 Departamento de Química, Facultad de Ciencias, Universidad Nacional de Colombia, sede Bogotá. Bogotá, Colombia.
Recibido: 22/02/11 - Aceptado: 15/04/11
RESUMEN
En este trabajo se presenta una versión rediseñada y optimizada del programa APMO (Any Particle Molecular Orbital). APMO es una implementación computacional del método del orbital molecular nuclear y electrónico (OMNE) en niveles de teoría Hartree-Fock (HF) y de perturbaciones de muchos cuerpos de segundo orden (MP2). En el método OMNE, tanto los núcleos atómicos como electrones se representan como funciones de onda. Este método permite un estudio directo de fenómenos en los que se presentan efectos cuánticos nucleares: efectos isotópicos, deslocalización nuclear, transferencia de protones, entre otros. La optimización realizada logró una marcada disminución en los tiempos de un cálculo global y permitió el uso de funciones de base electrónicas y nucleares con altos momentos angulares. Como ejemplo de las nuevas posibilidades del programa se presenta un estudio del efecto isotópico en complejos monohidratados y dihidratados de cobre (I) y cinc (II). En estos sistemas se encontró que la sustitución de protio por deuterio debilita el enlace oxígeno-metal.
Palabras clave: efectos cuánticos nucleares, efecto isotópico, Hartree-Fock, MP2, orbitales núcleo-electrónicos.
ABSTRACT
This paper describes the optimization of the overall calculation scheme and the implementations of an efficient system for calculate molecular integrals in the APMO software package (Any Particle Molecular Orbital). APMO is an implementation of the nuclear and electronic molecular orbital (NEMO) method at Hatree-Fock (HF) and MP2 levels of theory. In this method, both nuclei and electrons are represented as wave functions, which allow the study of phenomena where nuclear quantum effects are important, such as isotope effects, hydrogen bonding, proton transfer, and others. This optimization reached a marked decrease in global and molecular integrals calculation times and enabled the use ofbasis functions with angular momenta higher than d and allowed the calculation of systems with more than eight atoms. This paper also presents the application of the NEMO method to the study of the isotope effect on mono and dihydrated complexes of copper (I) and zinc (II). For these systems, we found that the substitution of a proton with a deuteron nucleus weakens the metal-oxygen bond.
Key words: Nuclear quantum effects, isotopic effects, Hartree-Fock, nuclear-electronic orbitals.
RESUMO
Este artigo descreve a otimização do sistema no cálculo global e a implementação de um sistema eficiente para calcular integrais moleculares no programa computacional APMO (Any Particle Molecular Orbital). APMO é uma implementação do método dos orbitais moleculares nucleares e eletrónicos (OMNE) no nível da teoria Hartree-Fock (HF) e o MP2. Neste método, tanto núcleos como elétrons apresentam-se como funções de onda permitirem o estudo dos fenômenos nucleares onde os efeitos quânticos são importantes, tais como efeitos de isótopos, pontes de hidrogênio, transferência de prótons, e outros. Com a otimização realizada, diminuiu o tempo do cálculo global e de integrais molecular; além disso, permitiu a utilização de funções de base com o momento angular superior a d eo cálculo de sistemas com mais de oito átomos. Este trabalho apresenta também a aplicação do método e NEMO para o estudo do efeito isotópico em mono-complexos e di-complexos de cobre (I) e zinco (II). Para estes sistemas, descobrimos que a substituição de um próton com um núcleo deuteron enfraquece o vínculo de oxigênio-metal.
Palavras-chave: efeitos quânticos nucleares, efeito do isótopo, Hartree-Fock, orbital núcleo eletrônico.
INTRODUCCION
La aproximación de Born-Oppenheimer (ABO) es una de las más importantes en la química cuántica. El empleo de esta aproximación ha posibilitado el estudio cuántico de sistemas con miles de átomos (1). A pesar del éxito de los métodos basados en la ABO, existen muchos ejemplos en los que el uso de esta aproximación no permite hacer una descripción directa y, en algunos casos, correcta de sistemas en los que los núcleos atómicos evidencian comportamientos cuánticos . Estos comportamientos son comúnmente conocidos como efectos cuánticos nucleares (ECN); entre ellos están las vibraciones y el tunelamiento nuclear, los efectos de isótopo, entre otros (2-4).
Los ECN pueden estudiarse teóricamente utilizando metodologías basadas en la ABO o metodologías que van más allá de esta aproximación. En las metodologías ABO se realizan cálculos de estructura electrónica, que se corrigen posteriormente incorporando los efectos de las masas y las velocidades nucleares. Entre las correcciones más comunes se encuentran la de Bell para el tunelamiento (5), la armónica para la energía de punto cero y la de masa para los efectos de isótopo. Entre los métodos más conocidos que van más allá de la ABO están los de orbitales núcleo-electrónicos (ONE) (2-4). En estos métodos, los núcleos que presentan comportamiento cuántico se tratan en el mismo nivel que los electrones en términos de orbitales moleculares expresados como combinaciones lineales de funciones gaussianas. Ya que las implementaciones computacionales de los métodos ONE presentan limitaciones relacionadas con el número de especies cuánticas no electrónicas soportadas (método NEO) (6) o la disponibilidad del software -métodos MCMO (7,8) y NOMO (9)-, anteriormente desarrollamos el programa computacional Any Particle Molecular Orbital (APMO) (10-12). Este ha servido como herramienta para estudiar ECN en el nivel de teoría Hartree-Fock (HF) y MP2 en sistemas que contienen mezclas de partículas cuánticas (10-16).
La versión original de APMO (10-12) presentaba limitaciones en cuanto al tipo de funciones base que podían ser utilizadas (hasta momentos angulares iguales a dos) o al número de átomos que podrían estudiarse en tiempos razonables. Estas limitaciones surgían por la ausencia de un esquema eficiente de los distintos procesos de cómputo, sobre todo del cálculo de integrales moleculares, que no solo limitaba el uso de funciones con alto momento angular (mayor de dos), sino que generaba un alto costo computacional. Como consecuencia, APMO no podía utilizarse para realizar cálculos de sistemas moleculares que contuvieran átomos de metales de transición y más de ocho átomos.
En este trabajo se presenta una nueva versión del programa APMO, la cual optimiza el esquema general de cálculo e implementa un sistema altamente eficiente para el cálculo de integrales moleculares, capaz de utilizar funciones base tipo gaussianas con momento angular mayor de dos. Para comprobar el aumento de la eficiencia del programa se realizaron cálculos de estructura electrónica de las moléculas He2 yCH4, los cuales se compararon con los obtenidos utilizando la versión inicial de APMO. De igual manera, para mostrar las nuevas posibilidades del programa APMO, se presenta un estudio del efecto isotópico de hidrógeno en la estabilidad del enlace metal-oxígeno para los complejos monohidratados y dihidratados de cobre (I) y cinc (II). Un estudio preciso de estos sistemas requirió el uso de funciones base electrónicas con momento angular f, para describir correctamente la polarización de los orbitales d del metal de transición. Los cálculos del efecto isotópico en pequeños clústeres solvatados son el primer paso para entender los efectos isotópicos de solvente observados en diversas propiedades.

MÉTODOS
Descripción del modelo OMNE
En esta sección se presentan las expresiones generales del método de orbitales nucleares y electrónicos. Los detalles completos pueden consultarse en los artículos originales (6-11). En este método, el hamiltoniano de un sistema que contiene mezclas de especies cuánticas y clásicas en unidades atómicas está dado por donde el primer término corresponde a la energía cinética de las partículas cuánticas, el segundo término corresponde alas interacciones entre pares de partículas cuánticas con cargas QjQy QjQ, el tercer término corresponde a las interacciones entre una partícula cuántica de carga QjQ y una clásica con carga QjCy el último término representa las interacciones entre partículas clásicas con cargas QjCy QjQ.y NQy NCson el número de partículas cuánticas y clásicas.
En el nivel de teoría Hartree-Fock, la función de onda total del sistema descrita por el hamiltoniano [1] se puede escribir como el producto de las funciones de onda de las diferentes especies cuánticas:

siendo Φ una función simétrica o antisimétrica, para bosones o fermiones según corresponda. La ecuación de Hartree-Fock para una partícula de la especie α tiene una forma análoga a la que aparece en el caso electrónico convencional:

donde α y β representan diferentes partículas cuánticas, hα(i) y es el hamiltoniano para una partícula,

Jα y Kα son los operadores de Coulomb y de intercambio, respectivamente,
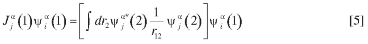

Los orbitales moleculares de la especie αse construyen a partir de una combinación Nfbαde funciones base tipo gaussiana (FTG),


La expresión de la energía total de un sistema con múltiples especies cuánticas es donde se considera una configuración electrónica en capa cerrada, y una configuración para las especies no electrónicas en capa abierta y máximo espín. hα, Fα representan las matrices de los operadores de partícula independiente y de Fock Pα es la matriz de densidad de la especie α.

Desarrollo computacional Optimización del esquema de cálculo global
Los orbitales atómicos de una especie dada se representan mediante funciones base tipo gaussianas (FTG). Una FTG [7], centrada en A, puede expresarse como donde r es la coordenada de la partícula, α es el exponente del orbital y n=nx + ny + nzcorresponde al momento angular de la FTG. A su vez, n¡ = nx, ny, nzcorresponde al i-ésimo componente de n. nise usará como el índice de momento angular en un sistema de coordenadas cartesianas. A partir de un mismo momento angular n se generan (n + 1) *(n + 2)/2 funciones con diferentes índices de momento angular. Estas conforman una capa de funciones, por ejemplo una capa s, n = 0 tiene 1 función, una capap, n = 1, tiene 3 funciones, etc.
En el diseño inicial de APMO (11), cada i-ésimo componente de una capa dada de FTG construye un objeto. Por ejemplo, para una base 4s, 3p, 2d se deben construir 25 objetos. La optimización se enfocó en generar objetos por cada capa completa y no por cada uno de sus i-ésimos componentes. De esta forma, la cantidad de objetos del ejemplo anterior se redujo de 25 a 9 disminuyendo la memoria requerida para este paso en la ejecución del programa. En la se presenta el esquema en notación UML del proceso de carga y la construcción de funciones gaussianas contraídas.
Implementación del sistema de cálculo de integrales
Se implementaron los algoritmos recursivos propuestos por Obara y Saika (17) y las adiciones planteadas por Head-Gordon y Pople (18) para el cálculo de integrales moleculares (overlap, energía cinética y atracción núcleo-electrónica) entre FTG para cualquier momento angular. La implementación de estos algoritmos se efectuó utilizando el lenguaje de programación
FORTRAN bajo el estándar 2003, siguiendo la filosofía de programación de APMO, la cual se basa en una adaptación del lenguaje FORTRAN al paradigma de programación orientada a objetos.
Para el cálculo de las integrales de repulsión electrónica se acopló la librería LIBINT (19). Esta contiene una colección de funciones altamente especializadas en el cálculo de integrales y derivadas de repulsión sobre FTG. Se diseñó una interfaz que genera los objetos requeridos por LIBINT para el cálculo de integrales y se desarrolló un algoritmo eficiente para organizar, almacenar y utilizar los resultados de forma adecuada.
RESULTADOS
Se realizaron cálculos de estructura electrónica convencional sobre los sistemas He2 y CH4 con diferentes funciones de base en un nivel de teoría RHF para evaluar la eficiencia de la nueva versión de APMO.
En la Tabla 1 se muestra el número de objetos generados en la ejecución del programa para el caso del CH4. Claramente se observa una disminución de la cantidad de objetos que se crean en tiempo de ejecución para todas las bases consideradas.
En la Tabla 2 se muestran las energías para el sistema He2, obtenidas mediante cálculos efectuados con la versión de APMO sin optimizar y optimizada. Se observa que la precisión alcanzada en la versión inicial del programa no se vio afectada por la optimización. Los espacios en blanco denotan que en la versión anterior de APMO era imposible realizar este cálculo, ya que las funciones base usadas para este cálculo poseen funciones gaussianas con momento angular f y g.
En la Tabla 3 se evalúa la eficiencia del sistema implementado para el cálculo de integrales y la eficiencia del ciclo de cálculo total. Se observa en ambas tablas que, a medida que aumenta el tamaño de la base, el ahorro es mayor.
La nueva implementación de APMO abre la posibilidad de estudiar sistemas que, para su correcta descripción, requieren funciones de base que incluyan FTG de momento angular mayor que d.Un ejemplo de estos sistemas son los complejos de metales de transición, los cuales incluyen funciones de polarización con momento angular f y g (20).
Para mostrar el potencial del programa APMO, presentamos un estudio del efecto isotópico de hidrógeno en la geometría y la energía de interacción de complejos monohidratados y dihidratados de cobre (I) y cinc (II). Las figuras 2 y 3 muestran una representación esquemática de los complejos. Para este estudio se optimizaron las geometrías de los complejos a nivel Hartree-Fock, usando como función de onda electrónica un determinante de Slater y como función de onda nuclear un producto de Hartree (21). Se usó como base electrónica la base 6-31G** (20), que incluye funciones de polarización f para el Cu y el Zn; como base para los núcleos de protio y deuterio, la base DZSPD (22). Los núcleos de oxígeno, cobre y cinc fueron considerados cargas puntuales.
En las Tablas 4 y 5se presentan los resultados de los cálculos de estructura electrónica regular a nivel HF/6-31G** de los complejos mono y dihidratados de cobre (I) y cinc (II) . En el caso de los complejos con cobre las distancias encontradas difieren en menos de 0,02 Â de los cálculos a nivel MP2 realizados por Lee et. al. (23). Asimismo, en el caso de los complejos con cinc, se encontraron diferencias de menos de 0,01 Â con los resultados de los cálculos B3LYP de Hartmann et al. (24). Estos resultados sugieren que los cálculos realizados a nivel Hartree-Fock son adecuados para describir estos sistemas.
En la Tabla 4 se muestran las distancias entre el metal y el átomo de oxígeno para los distintos isotopólogos de los complejos monohidratados de cobre (I) y cinc (II). Para ambos metales se observa que la sustitución de un núcleo de protio por uno de deuterio aumenta la distancia oxígeno-metal en 0,001 Â, a la vez que la sustitución de los dos núcleos de protio por deuterio aumenta dicha distancia en 0,002 Â. Estos resultados sugieren que el aumento en la masa del hidrógeno del agua debilita el enlace oxígeno-metal. La Tabla 5 también muestra que las energías de disociación del complejo en el catión metálico y la molécula de agua disminuyen con la sustitución de protio por deuterio: la energía de disociación del complejo Cu- D2O+ es 3 kJ/mol menor que la del complejo Cu- H2O+; a su vez, la energía de disociación del complejo Zn- D2O2+ es 6 kJ/mol, menor que la del complejo Zn-H2O2+. Estas tendencias permiten afirmar que el enlace Mn+-D2O es menos estable que el enlace Mn+-H2O.
La Tabla 5 presenta las distancias metal-oxígeno de los complejos de Cu+ y Zn2+ con dos moléculas de agua. Nuevamente se observa que la sustitución de protio por deuterio lleva a la elongación del enlace oxígeno-metal: los enlaces cobre y cinc con agua deuterada son, respectivamente, 0,001 Â y 0,002 Â, más largos que con agua no deuterada. En esta tabla se muestran también las energías de disociación de una molécula de agua de los complejos dihidratados:

Se observa que para romper el enlace Cu+-OD2 se necesitan 3 kJ/mol menos que para romper el enlace Cu+-OH2.Deforma similar, para romper el enlace Zn+2-OD2 se necesitan 5 kJ/mol menos que para romper el enlace Zn+2-OH2. Estos resultados nuevamente permiten concluir que la sustitución isotópica de protio por deuterio debilita el enlace metal-agua.
Estudios OMNE previos (10, 14, 15, 16, 22) han revelado que los isótopos más pesados son más electronegativos y que la carga negativa sobre el oxígeno es mayor en el H2O que en el D2O (22). Este hecho favorece la atracción electrostática entre el catión metálico y el agua no deuterada; por tanto, hace que este enlace sea más fuerte que el enlace metal-agua pesada. Tendencias similares se han observado para la sustitución isotópica en complejos p-catión (16).
CONCLUSIONES
Con la optimización propuesta del programa APMO se ha logrado reducir en promedio el tiempo de cálculo global en más de un 50%. El sistema de integrales implementado es de alta eficiencia; a medida que el tamaño de la base aumenta se puede ahorrar hasta un 40% de tiempo en un cálculo puntual de energía y demuestra tener la misma precisión que la obtenida con el sistema de integrales de la versión no optimizada. De igual manera, este sistema de integrales posibilita la realización de cálculos en APMO utilizando funciones base con momentos angulares superiores a d, lo que abre la posibilidad de estudiar complejos de metales de transición. En los ejemplos estudiados se encontró que la sustitución isotópica de hidrógeno en complejos catiónicos de cobre con una y dos moléculas de agua lleva a la elongación y el debilitamiento del enlace metal-agua.
REFERENCIAS BIBLIOGRÁFICAS
1. Peng, Q.; Zhang, X.; Hung, L.; Carter, E. A.; Lu, G. Quantum simulation of materials at micron scales and beyond. Phys. Rev. B. 2008. 78(5): 54118.
2. Nakai, H. Nuclear orbital plus molecular orbital theory: Simultaneous determination of nuclear and electronic wave functions without Born-Oppenheimer. Int. J. Quantum Chiem. 2007. 107(14): 2849-2869.
3. Ishimoto, T.; Tachikawa, M.; Nagashima, U. Review of multicomponent molecular orbital method for direct treatment of nuclear quantum effect. Int. J. Quantum Chem. 2009. 109(12): 2677-2694.
4. Udagawa, T.; Tachikawa, M. Multi-component molecular orbital theory. New York, Nova Science Publishers. 2009.
5. Bell, R. P. The tunnel effect in chemistry. London, Chapman and Hall. 1980.
6. Webb, S. P.; Iordanov, T.; Hammes-Schiffer, S. Multiconfigurational nuclear-electronic orbital approach: Incorporation of nuclear quantum effects in electronic structure calculations. J. Chem. Phys. 2002. 117(9): 4106-4119.
7. Tachikawa, M.; Mori, K.; Nakai, H.; Iguchi, K. An extension of ab initio molecular orbital theory to nuclear motion. Chem. Phys. Lett. 1998. 290(4-6): 437-442.
8. Tachikawa, M. Multi-component molecular orbital theory for electron and nuclei including manybody effect. Chem. Phys. Lett. 2002. 360 (5-6): 494-500.
9. Nakai, H. Simultaneous determination of nuclear and electronic wave functions without Born-Oppenheimer approximation: Ab initio NO+ MO/HF theory. Int. J. Quantum Chem. 2002. 86(6): 511-517.
10. González, S. A.; Aguirre, N. F.; Reyes, A. Theoretical investigation of isotope effects: The Any-particle molecular orbital code. Int. J. Quant. Chem. 2008. 108(10): 1742-1749.
11. González, S. A. ; Aguirre, N. F.; Reyes, A. APMO: un programa computacional para el estudio de efectos cuánticos nucleares mediante la teoría del orbital molecular electrónico y no electrónico. Rev. Colomb. Quim. 2008. 37(1): 93-103.
12. González, S. A.; Reyes, A. Nuclear quantum effects on the He2H+ complex with the nuclear molecular orbital approach. Int. J. Quantum Chem. 2010.110(3): 689-696.
13. González, S. A.; Reyes, A. Implemen-tación del método del gradiente analítico de la energía en la teoría del orbital molecular nuclear y electrónico. Rev. Colomb. Quim. 2009. 38(2): 117-125.
14. Forero, N.; González, S. A.; Reyes, A. Estudio teórico del efecto isotópico de hidrógeno en el aducto borano-carbonilo. Rev. Colomb. Quim. 2009. 38(2): 135-141.
15. Ortiz-Verano, I.; González, S. A.; Reyes, A. Estudio del efecto de isotópo de hidrógeno en los complejos M -H-H-F (M = Li, Na) Rev. Colomb. Quim. 2009. 38(2): 143-150.
16. Moreno, D. V.; González, S. A.; Reyes, A. Secondary hydrogen isotope effects on the structure and stability of cation-p complexes (Cation = Li+, Na+, K+ and p = acetylene, ethylene,benzene). J. Phys. Chem. A. 2010. 114(34): 9231-9236.
17. Obara, S.; Saika, A. Efficient recursive computation of molecular integrals over Cartesian Gaussian functions. J. Chem. Phys. 1987 . 84(7): 3963-3974.
18. Head-Gordon, M.; Pople, J. A. A method for two electron Gaussian integral and integral derivative evaluation using recurrence relations. J. Chem. Phys. 1988. 89(9): 5777.
19. Fermann, J. T.; Valeev, F. L. 2010. http://www.files.chem.vt.edu/chem-dept/valeev/software/libint/libint.html.
20. Rassolov, V. A.; Pople, J. A.; Ratner, M. A.; Windus, T. L. 6-31 G basis set for atoms K through Zn. J. Chem. Phys. 1998. 109(4): 1223.
21. Auer, B.; Hammes-Schiffer, S. Localized hartree product treatment of multiple protons in the nuclear-electronic orbital framework. J. Chem. Phys. 2010. 132(8): 084110.
22. Reyes, A.; Pak, M. V.; Hammes-Schiffer, S. Investigation of isotope effects with the nuclear-electronic orbital approach. J. Chem. Phys. 2005. 123(6): 064104.
23. Lee, H. M.; Min, S. K.; Lee, E. C.; Min, J. H.; Odde, S.; Kimb, K. S. Hydrated copper and gold monovalent cations: Ab initio study. J. Chem. Phys. 2005.122(6): 064314 .
24. Hartmann, M.; Clark, T.; vanEldik, R. Hydration and water exchange of zinc (II) ions. Application ofdensity functional theory. J. Am. Chem. Soc. 1997. 119(33): 7843-7850.