
INVESTIGACIÓN ORIGINAL
Javier Rodríguez Velásquez1
1MD, Univesidad Nacional de Colombia - Bogotá. Director del Grupo Insight.
Correspondencia:grupoinsight2025@yahoo.es
Resumen
Antecedentes: basados en una analogía lingüística aplicada al repertorio inmune B y T específicos, el sistema inmune se puede caracterizar por su grado de complejidad como se hace con los lenguajes naturales.
Material y métodos: este estudio es la aplicación de una ley matemática al repertorio inmune. Se aplicó la ley de Zipf-Mandelbrot, observada en los lenguajes naturales, al estudio del repertorio T específico contra el alergeno Poa p9.
Resultados: se observó un comportamiento a escala de la ley en el repertorio específico para el alergeno obtenido de un paciente alérgico en presencia y ausencia de interferón á, y en los clones de células Th. Los repertorios T en presencia y ausencia de interferón á se comportanfractalmente, con una dimensión fractal de 0.661165 y 0.923895 respectivamente.
Conclusión: el grado de complejidad del repertorio T contra el alergeno Poa p9 es una medida matemática objetiva y reproducible del repertorio inmune, la dimensión fractal es un parámetro matemático apropiado para caracterizar la fisiología del sistema inmune. Este comportamiento fractal puede tener implicaciones generales para la inmunología.
Palabras clave: sistema inmune, interferon tipo I, células clonales, alergenos, linfocitos T, Poa, ley de Zipf-Mandelbrot, fractal, dimensión fratal.
Summary
Background: based on a linguistic analogy applied to the immune specific B and T repertoires the immune system it has been characterized by the degree of fractal complexity like the one observed in the natural languages.
Material and methods: this study is the application of a mathematical law to the immune repertoire. The Zipf-Mandelbrot law, observed in the natural languages, was applied to the study of the specific T repertoire against the allergen Poa p9.
Results: the scale behavior of the law was observed in the specific repertoire from an allergic patient, with a without alfa interferon, like in Th cells clones. Conclusion: complexity degree of T repertoire against Poa p9 allergen can be identified by fractal dimension, as a appropriate mathematical parameter to characterize the physiology of the immune system, this fractal behavior has general implications for the immunology.
Key words: Immune system, interferon type I, clone cells, allergens, T-Lymphocytes, Poa, Zipf-Mandelbrot law, fractal, fractal dimension.
Introducción
La geometría fractal, nuevo tipo de geometría, desarrollado por Benoît Mandelbrot, permite describir objetos irregulares (1-3). Con la geometría fractal es posible calcular la dimensión del objeto irregular (4,5), obteniendo una caracterización matemática objetiva. En la actualidad se utilizan diferentes definiciones de dimensión fractal. Si el objeto es abstracto, como en el caso del conjunto de Cantor, el triángulo de Sierpinski o la curva de Koch, la dimensión Hausdorff es la más aplicada (3,5). Si los objetos presentan la propiedad de superposición entre sus partes, como lo hacen los objetos naturales, se consideran fractales salvajes y su dimensión se calcula con el método de Box-Counting (5). Con esta metodología se han caracterizardo objetivamente (6-10) células, órganos y tejidos, además se ha utilizado para diferenciar tejidos y redes vasculares sanas de cancerígenas (11,12). Trabajos con modelos de experimentación animal en arterias coronarias diferenciaron matemáticamente las arterias sanas de las enfermas lo que sugiere su utilidad como método de evaluación de las intervenciones moleculares (13).
Otro tipo de fractal, es el estadístico, descubierto en los lenguajes naturales donde la frecuencia de distribución de las palabras se describe mediante la ley de Zipf-Mandelbrot demostrando una estructura ordenada, jerarquizada y estática, que evalúa el grado de complejidad del sistema (3). La ley de Zipf-Mandelbrot es una ley empírica que permite estudiar cualquier fenómeno que se pueda caracterizar por la aparición de frecuencias de alguna variable. Zipf desarrolló una organización jerárquica de la aparición de palabras en un texto a la cual asignó rangos haciendo corresponder a la mayor frecuencia el menor rango, con los rangos aumentando en forma inversamente proporcional a las frecuencias, se evidenció un comportamiento hiperbólico del fenómeno.
Posteriormente Mandelbrot, mediante una linealización logarítmica de las frecuencias y de los rangos definió la dimensión fractal estadística calculando el inverso de la pendiente de esta linealización. El sistema inmune de los vertebrados posee dos tipos de respuestas específicas de memoria: la humoral de linfocitos B y la celular de linfocitos T. Ambas se expresan en lo molecular por receptores de membrana que median la reactividad de los linfocitos T y B para antígenos específicos generando una respuesta inmune.
La reorganización de los genes implicados en la codificación de los receptores de membrana constituye los repertorios inmunes T y B, proceso de alta complejidad biológica según evidencia experimental (14-16).
Análisis fractales recientes que usaron una analogía lingüística, en donde las letras representaban reacciones positivas o negativas, las palabras, los patrones de reactividad y el discurso, el repertorio particular de estudio, se encontró un comportamiento fractal estadístico como el observado en los lenguajes naturales (17,18), en el repertorio B contra el Ag pr8 del virus de la influenza y en el repertorio de linfocitos T citotóxicos sanos. En uno de estos trabajos (18) la respuesta inmune T de ratones irradiados perdía el orden fractal mientras que en ratones atímicos se disminuía drásticamente su complejidad, sugeriendo que ésta puede ser una metodología de evaluación del estado de salud o enfermedad. Este trabajo parte primero del estudio de la organización jerárquica de las palabras de los lenguajes naturales con su correspondiente grado de complejidad y su aplicación en forma analógica al repertorio inmune B y T, respecto a las frecuencias de mayor a menor de clones T o B específicos en trabajos experimentales en ratones Balbc B10.D2, B10.BR (17,18), evaluándose la respectiva dimensión fractal, con asociaciones sobre normalidad y enfermedad, para finalmente buscando repertorios de aplicación clínica, encontrar el trabajo de Parronchi y su grupo, quienes en inmunoterapias en presencia y ausencia de interferón, molécula inmunomoduladora del repertorio inmune, con pacientes alérgicos encontraron frecuencias de clones de mayor a menor de linfocitos T específicos de repertorios T contra el Poa p9 los cuales eran candidatos para realizar los cálculos matemáticos correspondientes.
Con este análisis matemático de Zipf-Mandelbrot se busca establecer el comportamiento fractal estadístico del repertorio T específico para el alergeno Poa p9 en presencia y ausencia de interferón α y las frecuencias de células Th en ausencia de interferón á, como también plantear posibles metodologías sobre el diagnóstico y la evaluación del tratamiento en alergias, junto con algunas ideas de aplicación general a la inmunología.
Definiciones
Dimensión fractal estadística: grado de complejidad o irregularidad del sistema. La dimensión fractal estadística D toma los valores entre 0 y 1.

Donde:
Repertorio inmune: es el número total de especificidades antigénicas reconocidas de los linfocitos en un individuo. Se calcula que se puede distinguir al menos 109 determinantes antigénicos diferentes en el sistema inmunitario de los mamíferos. En este trabajo se evalúan las especificidades antigénicas reconocidas por linfocitos T de seis péptidos del alérgeno Poa p9.
Citocina: moléculas protéicas que se producen durante las fases efectoras de la inmunidad natural y específica y sirven para mediar y regular las respuestas inmunitarias e inflamatorias.
Patrones Th: proporciones predominantes en la producción de citocinas de linfocitos durante las fases efectoras de la respuesta inmune. Para este trabajo el patrón Th2: produce interleucina (IL)4, IL5 y no produce interferón gama (IFNã); el patrón Th1 o Th0: produce IFNã y limitadas cantidades de IL 4 y IL5 o no las producen.
Analogía lingüística: en este trabajo las palabras representadas por las frecuencias de clones y el discurso es el repertorio particular contra el alergeno.
Material y métodos
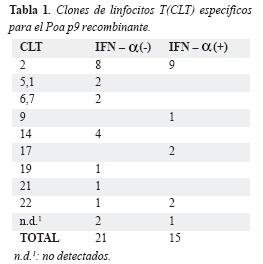
Parronchi y cols (19) desarrollaron un estudio sobre los efectos del interferón á en el repertorio T específico contra el alergeno Poa p9. El conjunto de clones del repertorio T específico contra el alergeno fue aislado de sangre periférica de un paciente alérgico buscando establecer los repertorios de cada respuesta T específica contra el alergeno en presencia y ausencia de interferón á recombinante, y de los patrones Th. Primero desarrollaron un panel de clones de células T específico para el Poa p9, establecido de sangre periférica de un donador con rinitis estacional y con hipersensibilidad inmediata cutánea al Poa p9, con péptidos sintéticos específicos, P5, P11, P20, P23, P25, P26 del alérgeno, para luego examinar el patrón de secreción de citocinas en cultivos en presencia y ausencia de interferón á, evaluando la secreción de citocinas como IFNã IL 4 y IL5 y estableciendo el patrón Th para cada cultivo y finalmente secuenciar las cadenas genéticas á del receptor T y establecer el repertorio T especí fico de donde fueron obtenidos los datos del repertorio T contra el alergeno (Tabla 1).
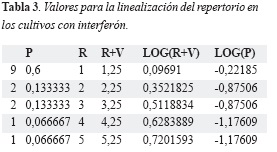
Las distribuciones de frecuencias del repertorio se obtienen dividiendo el número de clones específicos hallados entre el número total de clones encontrados y se organizan en orden decreciente resultando un comportamiento hiperbólico, ley de Zipf (Figura 1), esta expresión puede ser linealizada redefiniendo las funciones y evaluando su logaritmo para calcular la dimensión fractal como describe Burgos (17, 18), (Tabla 2 y Tabla 3).


Resultados
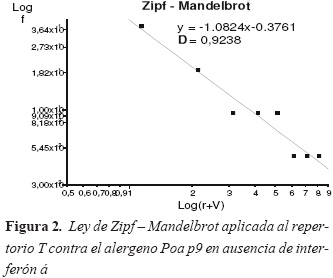
Los repertorios T en presencia y ausencia de interferón á se comportan fractalmente, siendo la dimensión fractal de 0.661165 y 0.923895 respectivamente. En la figura 2 se observa la linealización en ausencia de la citoquina. La complejidad para los clones de patrones de células Th en ausencia de interferón á fue ser de 0.633676.
La tabla 4 muestra los valores de la dimensión fractal D en el caso del repertorio T producido contra el alergeno Poa p9 en presencia y ausencia de interferón á y del patrón de células Th, mostrando las respectivas variaciones en los grados de complejidad de la respuesta inmune.

Discusión
Este es el primer trabajo en el que se calcula la dimensión fractal del repertorio T contra un alergeno específico. Este repertorio mostró
una distribución hiperbólica y un comportamiento fractal en presencia y ausencia de interferón á en el cultivo. La dimensión fractal del repertorio para el alergeno tratado con el interferón á mostró que el grado de complejidad fue menor en presencia que en ausencia de la citocina. De igual forma se calculó la dimensión fractal del patrón Th2 encontrando concordancia con la analogía lingüística, evidenciando que los repertorios y patrones Th pueden expresarse en forma de una ley matemática objetiva y reproducible para la fisiología inmune. De acuerdo con esto la dimensión fractal caracteriza matemáticamente y de manera precisa la complejidad de los repertorios contra alergenos y sus posibles tratamientos, interferón á en este caso, logrando hacer correlaciones entre resultados in vitro y las caracterizaciones matemáticas.
Los trabajos de Mandelbrot se pueden aplicar a cualquier texto coherente por lo que es una ley empírica general, así como la analogía lingüística es aplicable al sistema inmune, pues los clones de linfocitos presentan distribuciones de frecuencias a las que se les pueden asignar los rangos correspondientes, en cualquier experimento realizado con repertorios, lo que implica la aplicación general al sistema inmune y sus implicaciones al verlo como un lenguaje estructurado (17,18), por lo que se plantea la generalidad del trabajo a pesar de un solo experimento con y sin interferón á y el experimento que mide los patrones Th.
El cálculo del grado de complejidad del patrón Th2 predominante contra el alergeno en ausencia de la citocina muestra como se pueden caracterizar matemáticamente de manera objetiva patrones de células Th, lo que por la generalidad de estos patrones tiene implicaciones no sólo en las alergias sino en todas las áreas de la inmunología, además de la importancia clínica en inmunoterapias. En algunos casos los tres patrones Th no se encuentran, lo que podría solucionarse suponiendo una frecuencia mínima de uno para la ausente, aplicando la metodología y realizando así las correlaciones. Considerando el sistema inmune como un sistema que se autoorganiza, de acuerdo al índice de auto organización que será llamado "criticalidad autoorganizada" (20), el sistema inmune actuaría dentro de puntos críticos fisiológicamente efectivos, como se evidencia en las correlaciones de salud y enfermedad en ratones sanos y enfermos cuyas dimensiones fractales se encuentran entre 0 y 1 y mayores de uno respectivamente. Desde est as consideraciones el estudio de las alergias y la evolución de los patrones Th predominantes podría generar la búsqueda de una comprensión desde leyes matemáticas de la fisiología inmune, su evolución propia y una forma de aplicarla en estudios experimentales y clínicos.
Conclusiones
El grado de complejidad del repertorio T contra el alergeno Poa p9 es una medida matemática objetiva y reproducible de la organización y funcionamiento del sistema inmune. El repertorio T específico contra el alergeno Poa p9 en presencia y ausencia del interferón á presenta comportamiento fractal, con un menor grado de complejidad en presencia de la citocina. El patrón de células Th en ausencia de interferón á se comporta de acuerdo a la ley de Zipf- Mandelbrot, lo cual permite una caracterización matemática objetiva y reproducible del sistema. El grado de complejidad caracteriza matemáticamente de manera precisa los repertorios contra alergenos in vitro y sus posibles inmunoterapias, interferón á en este caso.
Agradecimientos
A mis Amigos. Al grupo Insight, por su apoyo incondicional en la realización de este artículo. Al Dr. Rubiano y al Dr. Gallego por su apoyo incondicional a mis investigaciones. A Javier Burgos por enseñarme esta metodología y escuchar personalmente este trabajo.
Referencias
1. Mandelbrot B. Introducción. En: Los Objetos Fractales. Barcelona: Tusquets Editores SA;2000:13-26.
2. Mandelbrot B. ¿Cuánto mide la costa de Bretaña?. En: Mandelbrot B. Los Objetos Fractales. Barcelona: Tusquets Eds. SA; 2000:27-50.
3. Mandelbrot B. The Fractal Geometry of Nature, San Francisco Freeman, 1972, 341-348.
4. Peitgen H, Jürgens H, Saupe D, Forewords. En: Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag. 1992:1- 7.
5. Peitgen H, Jürgens H, Saupe D. Length area and dimension. Measuring complexity and scalling properties. En: Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag. 1992:183-228.
6. Goldberger A, West BJ. Fractals in physiology and medicine. The Yale Journal of Biology 1987;60:421-35.
7. Goldberger A, Rigney D, West B. Chaos and fractals in human physiology. Sci Am 1990;262:42-49.
8. West BJ. Fractal Physiology and Chaos Medicine. London. World Scientific Publishing Co. 1990.
9. Goldberger AL. Fractal dynamics in physiology: Alterations with disease and angin. PNAS. 2002; 99:2466-2472.
10. Goldberger AL. Non-linear dynamics for clinicians: chaos theory, fractals, and complexity at the bedside. Lancet. 1996; 347: 1312 - 1314.
11. Luzi P, Bianciardi G. Fractal Analysis in Human Pathology. Annals New York. Academy of Sciences. Vol: 255-257.
12. Baish J, Jain R. Fractals and Cancer. Cancer Research 2000; 60:3683-3688.
13. Rodríguez J, Mariño M, Avilán N, Echeverri D. Medidas fractales de arterias coronarias, un modelo experimental en reestenosis, armonía matemática intrínseca de la estructura arterial. Rev Col Cardiología a 2002; 10:65-72.
14. Grandien A, Modigliani Y, Freitas A, Anderson J, Coutinho A. Positive and negative selection of antibody repertoires during B-cell differentiation. Immunol. Rev. 137, 53-89.1994.
15. Lichtman A. Pober J. Inmunología Celular y Molecular, Interamericana-McGraw-Hill. 1995.
16. Rajewsky K. Clonal selection and learning in the antibody system. Nature. 1996: 751-758.
17. Burgos J. Fractal representation of the immune B cell repertoire. Biosystems 39,19-24.
18. Burgos J, Moreno-Tovar P. Zipf-scaling behavior in the immune system. Biosystems 39, 227-232.
19. Parronchi, Mohapatra S, Sampognaro S, Giannarini L, Wahn U, Chong P, et al. Effects of interferon á on cytoquine profile, T cell receptor repertoire and peptide reactivity of human allergen-specific T cells. Eur J immunol 1996;26:697-703.
20. Bak P, Tang C, Wiesenfeld K. The self -organized criticality: an explanation of 1/s noise.Phys Rey. Lett 1987, 59: 381-384.