
INVESTIGACIÓN ORIGINAL
Javier Rodríguez Velásquez1, Signed Prieto Bohórquez2, Liliana Ortíz Salamanca3, Alejandro Bautista Charry4, Pedro Bernal5 , Nicolás Avilán Vargas6
1.Director Grupo Insight. MD. Facultad de Medicina, Universidad Nacional de Colombia, Bogotá.
2.Investigadora Grupo Insight
3.Investigadora Grupo Insight. Delineante de Arquitectura. Colegio Mayor de Cundinamarca.
4.MD. Profesor Asociado Facultad de Medicina Universidad Nacional de Colombia, Bogotá.
5.Investigador Grupo Insight. Estudiante de Ingeniería de Sistemas Universidad Nacional de Colombia, Bogotá.
6.Investigador Grupo Insight. Físico, Universidad Nacional de Colombia, Bogotá.
Correspondencia:grupoinsight2025@yahoo.es
Resumen
Antecedentes. El actual diagnóstico clínico de la monitoría fetal presenta problemas de objetividad y reproducibilidad, sin embargo el análisis físico y matemático del trazado lleva a caracterizaciones objetivas y reproducibles de la dinámica cardíaca fetal.
Objetivo. Desarrollar una nueva metodología diagnóstica de la monitoría fetal aplicando las concepciones de la teoría de sistemas dinámicos y la ley de Zipf-Mandelbrot para evaluar la complejidad del trazado a partir de la aparición de Componentes Dinámicos del Sistema (CDS)
Material y métodos. Se evaluaron 50 monitorias de mujeres gestantes divididas en dos grupos: grupo A, 40 gestantes con estados de interés en la práctica clínica durante el desarrollo del embarazo, por ende, diagnosticadas con enfermedades y grupo B, 10 mujeres con embarazo normal. Se definieron cuatro prototipos matemáticos de salud y enfermedad para la evaluación y diagnóstico de cualquier dinámica cardíaca y se evalúo su grado de complejidad aplicando la ley de Zipf-Mandelbrot.
Resultados. Un feto sano presenta una autoorganización matemática caracterizada por una dimensión fractal mayor que cero, la ausencia de CDS invertidos pronunciados (CDSiP) y un valor mayor a 12 en la suma de apariciones de CDS con cambios de frecuencias entre 15 y 25 latidos por minuto. La enfermedad se caracteriza por la presencia de uno o más CDSiP o por la pérdida de complejidad en el grupo de CDS de altura 5 ó 10, o por la suma menor de 12 en las apariciones de CDS con alturas entre 15-25 latidos por minuto y por combinaciones de éstos parámetros. De acuerdo a las medidas obtenidas tres de cada diez embarazadas de los grupos A y B tienen un diagnóstico equivocado.
Conclusión. Esta es una nueva metodología matemática de evaluación diagnóstica de la dinámica cardíaca fetal; objetiva y reproducible en la práctica clínica diaria.
Palabras clave: investigación fetal, monitoreo fetal, métodos, diagnóstico, diagnóstico prenatal, matemáticas, ley de Zipf-Mandelbrot.
Summary
Key words: fetal research, fetal monitoring, methods, diagnosis, prenatal diagnosis, mathematics, Zipf-Mandelbrots law.
Introducción
La teoría de los sistemas dinámicos describe las leyes que gobiernan el comportamiento de las variables de un sistema con las que se define el estado y se predice la evolución del mismo. El comportamiento de una variable dinámica puede ser representado por diagramas de fases o atractores, los cuales caracterizan si el sistema es predecible o impredecible (1,2). Goldberger, basado en la teoría de los sistemas dinámicos aplicada a la fisiología, planteó que los sistemas enfermos se caracterizan por presentar alta periodicidad o excesiva aleatoriedad siendo el comportamiento intermedio de dichos extremos característico de la salud (3).
En la naturaleza se encuentran objetos irregulares los cuales se caracterizan a través de su dimensión fractal (4,5). Esta es una medida adimensional propia de la geometría fractal desarrollada por Benoît Mandelbrot (6-8). Otro tipo de caracterización fractal se obtiene aplicando la ley Zipf-Mandelbrot, ley empírica que evalúa el grado de complejidad o coherencia de un sistema a partir del análisis de distribuciones de frecuencia de determinada variable del sistema del que se obtiene la dimensión fractal (9,10,11); esta ley ha sido usada para caracterizar la complejidad de la respuesta inmune del repertorio T (12, 13).
Recientemente, Rodríguez (14) evidenció el comportamiento fractal del repertorio inmune T y el patrón Th contra un alergeno específico, el Poa P9, de un paciente alérgico en presencia y ausencia de interferón alfa, encontrando correlaciones clínicas y matemáticas respecto a la salud y a la enfermedad y evaluando inmunoterapias de forma objetiva y reproducible.
La monitoría es el examen de bienestar fetal más frecuentemente utilizado en la práctica clínica diaria y se evalúa a partir de guías definidas de interpretación; sin embargo, la evaluación diagnóstica carece de reproducibilidad. En estudios previos se han desarrollado las primeras caracterizaciones matemáticas de la dinámica cardíaca fetal; la primera de ellas (15) se hizo definiendo cuatro componentes dinámicos del sistema (CDS), los cuales fueron medidos en el trazado y posteriormente analizados mediante el cálculo de probabilidades. Se logró una caracterización objetiva y reproducible de la dinámica cardíaca fetal independiente de la clasificación por factores de riesgo o edad gestacional. En un estudio posterior (16) se definieron cuatro prototipos de monitoría, a partir de una reinterpretación de la mencionada concepción salud enfermedad planteada por Goldberger, encontrando que los trazados con tendencia a la periodicidad presentan valores menores en las probabilidades de sus CDS.
El propósito de la presente investigación es definir criterios matemáticos para la evaluación diagnóstica de la monitoría fetal con una reinterpretación de la concepción saludenfermedad desde la teoría de los sistemas dinámicos, además de evaluar la complejidad de la distribución de CDS aplicando la ley de Zipf-Mandelbrot, sin los conceptos tradicionales de línea de base, ni evaluaciones epidemiológicas ni estadísticas.
Definiciones
Definición físico-matemática de salud-enfermedad, patrón de oro de comparación: la normalidad será definida por dos prototipos de monitorias normales, sin dudas en su diagnóstico, denominados como P3 y P4.
La enfermedad es definida por la evaluación matemática aclarada en la metodología de una monitoria prácticamente plana y/o con sufrimiento fetal agudo (SFA) sin dudas en su diagnóstico denotadas como monitorías prototípicas P1 y P2.
Los prototipos P1, P2, P3 y P4 son los patrones de comparación diagnóstica con los parámetros matemáticos escogidos: dimensión fractal, sumas de grupos de CDS y CDSiP.
Componentes dinámicos del sistema (CDS): cambios de la frecuencia cardíaca fetal durante un período, definidos en intervalos de múltiplos de cinco latidos por minuto en cambios de la frecuencia y múltiplos de cinco segundos en el tiempo. Es decir, son áreas de frecuencia por tiempo diferenciándose cada CDS por los valores en cambios de la frecuencia de a cinco. El total de componentes dinámicos se obtiene considerando todas las posibilidades de tiempos y frecuencias en múltiplos de cinco. Con los CDS se evalúan tanto los aumentos como las disminuciones de la frecuencia cardíaca fetal. Cuando no hay cambio de la frecuencia en latidos por min no hay CDS. La notación que se utilizará para cada CDS estará dada por su duración en segundos y su cambio en la frecuencia en latidos por minuto; por ejemplo, un CDS de tiempo de 20 seg y un cambio en la frecuencia de 40 latidos por minuto se expresará como un CDS de 20x40.
CDS invertido (CDSi): es un CDS que describe una disminución en la frecuencia cardíaca.
CDSi pronunciado (CDSiP): es un CDSi con una duración mayor a 20 segundos y un cambio en la frecuencia mayor a 50 latidos por minuto (TxH) mayor que (20x50).
Grupo de CDS: conjunto de los CDS con un mismo cambio en la frecuencia en latidos por minuto.
Aclaración: cada CDS es un área como fue definida de manera similar a como se hace en la evaluación convencional de las aceleraciones y desaceleraciones, sólo que en este trabajo se evalúan todos los tipos de cambios en la frecuencia y en el tiempo.
Dimensión fractal estadística (12,13): medida adimensional del grado de complejidad de un sistema que se obtiene con el inverso de la pendiente de la linealización logarítmica de la ley de potencias, y su ecuación es:

donde s es el rango asignado a cada frecuencia, P es la frecuencia de aparición de cada CDS en el trazado de la monitoría, V está definida por V= 1/N-1 donde N es el número de frecuencias medidas y F es geométricamente el punto de corte con el eje vertical de la recta obtenida en la linealización.
Metodología
Se evaluaron 50 registros tomados con un monitor fetal marca Corometrics, en el que se registró la frecuencia cardíaca fetal en el tiempo, con una velocidad de tres centímetros por minuto y una escala de 30 latidos por minuto por cada centímetro de papel.
Se evaluaron las monitorías realizadas a 40 gestantes diagnosticadas como enfermas y con estados de interés en la práctica clínica (Tabla 1), grupo A, y 10 que presentaron embarazo normal, grupo B, con edad gestacional mayor de 28 semanas. Las monitorías del grupo A fueron tomadas de gestantes que ingresaron al servicio del Instituto Materno Infantil y las del grupo B del Hospital de Engativá.
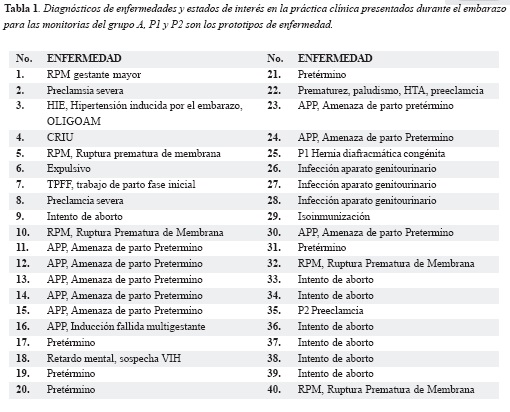
Criterios de selección: las pacientes escogidas se dividieron en dos grupos para poder hacer una diferenciación matemática entre salud y enfermedad con procesos habituales en la práctica clínica. Por esta razón el grupo A presenta pacientes con estados de interés en la práctica clínica en el desarrollo del embarazo y diagnosticas de enfermedad, por ejemplo preclampsia. Las monitorias definidas como prototipos diagnósticos fueron escogidas basándose en una reinterpretación de la concepción saludenfermedad de los sistemas dinámicos (3), en donde el trazado aleatorio de dicha concepción es reemplazado por una monitoría con desaceleraciones pronunciadas y con el diagnostico de preclampsia evidenciando SFA. El trazado prácticamente plano permanece como enfermedad y dos monitorias de pacientes sin dudas clínicas, ni de interpretación de la monitoria se escogen como normales. También fueron escogidas porque pueden representar y ser comparadas con cualquier tipo de trazado.
Los CDS de cada trazado fueron medidos con una rejilla de seis cm de base por cinco cm de altura, la cual contiene todos los CDS posibles. La rejilla fue diseñada con divisiones horizontales cada 5 latidos/min, y verticales cada 5 seg. El proceso de medición consistió en llevar la rejilla a través del registro de izquierda a derecha midiendo los CDS que describen aumentos y disminuciones en el sentido en el que va el trazado de la monitoria, midiendo el CDS más grande que esté contenido en determinada variación de la frecuencia cardíaca. El número total de apariciones se obtuvo sumando una vez los CDS más pequeños dentro de los grandes, evaluando cada aumento y disminución en la frecuencia cardíaca de forma consecutiva en el trazado, sin tomar en cuenta las interrupciones. Cuando no se presentaron cambios en la frecuencia cardíaca no se midió ningún CDS.
Para la aplicación de la ley Zipf-Mandelbrot (10, 14) se obtuvo el comportamiento hiperbólico para las distribuciones de frecuencias de CDS a las que se les asignó un rango que es uno para la frecuencia máxima y toma valores naturales consecutivos para las siguiente frecuencias de CDS, posteriormente evalúa la función logaritmo en las variables para realizar una linealización con el método de mínimos cuadrados (17) y finalmente obtener la dimensión fractal.
Para determinar diferencias matemáticas entre salud y enfermedad como evaluación diagnóstica de cada monitoría fetal, se evalúan los cuatro prototipos definidos que especifican matemáticamente las características de salud y enfermedad a partir de los siguientes parámetros: la dimensión fractal de cada uno de los dos grupos de CDS que presenten mayores valores en las frecuencias de aparición, la cantidad de CDS en cada grupo mediante la suma de las frecuencias de aparición de CDS en los grupos entre 15-25 latidos por minuto y la aparición de CDS invertidos que evidencien matemáticamente el sufrimiento fetal agudo. Finalmente, con estos parámetros encontrados en los prototipos definidos se realiza la comparación matemática con cada una de las restantes monitorías.
Análisis matemático. Las diferencias en los parámetros matemáticos evaluados, las sumas de CDS, las dimensiones fractales y los CDSiP, de los prototipos diagnósticos se comparan con el resto de las monitorías.
El análisis de las dimensiones fractales se realiza según la analogía lingüística, dando un significado al valor de la dimensión fractal igual a cero, entre 0-1 y mayor que 1, de acuerdo a la interpretación de la ley de los lenguajes naturales aplicada a los prototipos. Posteriormente se realiza el mismo análisis para cada una de las monitorias de los dos grupos para ser comparadas con los prototipos diagnósticos.
Considerando que la aplicación de la ley de Zipf-Mandelbrot requiere de una distribución hiperbólica, en el caso en que se presenten tres tipos de CDS o menos no es posible observar el comportamiento hiperbólico ni evaluar su grado de complejidad con ésta metodología, por esto a las monitorias que presenten tres CDS o menos se les asignará la dimensión fractal cero.
Las diferenciaciones de saludenfermedad obtenidas de los parámetros diagnósticos, de las monitorias prototípicas escogidas evalúan cuantificaciones matemáticas estrictas aplicables a cualquier caso particular independientemente de la selección de poblaciones muestrales y de análisis estadísticos.
Resultados
En total se desarrollaron 1440 posibles CDS, 720 aumentos y 720 disminuciones en la frecuencia cardíaca fetal de los cuales se midieron 158 variedades de CDS para caracterizar cualquier monitoría, 75 CDS aumentos y 83 disminuciones diferentes. Se encontró que los grupos de CDS de altura 5 y 10 latidos por minuto presentaron una mayor frecuencia de aparición, por lo que son considerados determinantes en la dinámica cardíaca fetal y son evaluados con la ley de ZipfMandelbrot.
El diagnóstico matemático de la dinámica cardíaca de un feto sano se caracteriza por la ausencia de CDSiP además de la existencia de un grado de complejidad mayor que cero en los grupos evaluados de altura de 5-10 latidos por minuto y por presentar un valor mayor a 12 en la suma de la frecuencia de aparición de los CDS con un altura entre 15-25 latidos por minuto. Mientras que la dinámica cardíaca para un feto enfermo es diagnosticada por una dimensión fractal de cero en el grupo de CDS de altura 5 ó 10, o la presencia de mínimo un CDSiP, o que el valor de la suma de las frecuencias de aparición de CDS entre 15-25 sea menor o igual que 12 (Tabla 2)y(Tabla 3).


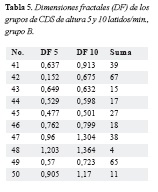
En el grupo A las dimensiones fractales del grupo de CDS de altura cinco estuvieron entre 0,314 y 1,683, mientras que en el grupo de altura 10 se presentaron entre 0-4,495. En el grupo B las dimensiones fractales del grupo de CDS de altura 5 estuvieron entre 0,152-1,203, mientras que en el grupo de altura 10 se presentaron entre 0 y 1,350; (Tabla 4) y (Tabla 5). Se encontraron ocho dimensiones fractales mayores a uno en los CDS de altura 5 del grupo A y 1 en el grupo B. En los CDS de altura 10 se encontraron 18 dimensiones fractales mayores a 1 en el grupo A y tres en el grupo B.

Los parámetros matemáticos evaluados diferencian sin dudas la salud, P3 y P4, de la enfermedad, P1 y P2, además de proporcionar cuantificaciones preventivas que al variar los valores de una monitoria a otra en el tiempo pueden alertar sobre la presencia de enfermedad.
Al comparar el diagnóstico matemático aquí desarrollado con el que se realiza convencionalmente en la clínica se encuentra que tres de cada diez monitorías del grupo A y tres de cada diez del grupo B tienen un diagnóstico equivocado. Sin embargo, esta metodología puede diferenciar cualquier tipo de monitoria sin necesidad de este tipo de muestras poblacionales.
Discusión
Este es el primer trabajo en el que se obtiene un diagnóstico matemático de la monitoría fetal a partir de la ley de Zipf-Mandelbrot aplicada a dos grupos de CDS, de altura 5 y 10 latidos por minuto, además del análisis de las cantidades totales de CDS de cambios de frecuencia de 15,20 y 25 latidos por minuto basado en una reinterpretación de la concepción salud-enfermedad de los sistemas dinámicos y en el análisis de la aparición de CDS en la monitoría, partiendo de cuatro registros prototípicos y su comparación con el resto de las monitorías. La evaluación diagnóstica tradicional, reactiva o no reactiva, se ve enriquecida en el proceso de evaluación matemática ya que ésta diferencia el comportamiento saludable en la dinámica cardíaca para cada caso particular, más específicamente, con las diferentes distribuciones de CDS obtenidas y con los diferentes parámetros evaluados. Todos los valores matemáticos y las evaluaciones realizadas son finitos y sus cuantificaciones objetivas y reproducibles comparado s con la evaluación clínica convencional.
Este método diagnóstico desarrolla una simplificación en la evaluación de la monitoría, ya que requiere pocos criterios, definidos a partir de medidas objetivas y reproducibles, en comparación con la metodología clínica tradicional que requiere de cinco parámetros de evaluación, además de siete subparámetros aclaratorios, que a pesar de ello conducen a un diagnóstico con deficiencias en su objetividad y reproducibilidad (18-22). Con esta metodología matemática no se presentan confusiones metodológicas inter e intraobservador por la forma de medición unívoca que se deben realizar para obtener el diagnóstico. En este trabajo uno de los casos estudiados (Tabla 6), finalizó con la muerte del neonato. Esta monitoría fue evaluada como no reactiva según los parámetros clínicos convencionales, al analizarla desde esta nueva metodología la monitoría fue diagnosticada como enferma, pues la suma de CDS de cambios de frecuencias de 15, 20 y 25 latidos por minutos es de cero, lo cual implica que esta metodología pue de tener un carácter preventivo.

Para diferenciar las monitorías sanas y enfermas con el parámetro de sumas de CDS que representan cambios de frecuencias de 15, de 20 y 25 latidos por minuto, se tomó el límite de 12 por la comparación del prototipo enfermo P1 con una suma de cero y valores de hasta 12 para las monitorías diagnosticadas con enfermedad.
En el trabajo anteriormente desarrollado (15), la principal dificultad metodológica estaba en la aparición de discontinuidades en el trazado, los fundamentos matemáticos de este diagnóstico obvian esa dificultad, salvo en el caso en que el tiempo de interrupción sea comparable al requerido por una disminución pronunciada, en tal caso sería necesario repetir el examen. Siguiendo esta metodología en muchos casos no es necesario tomar los 20 minutos del registro, pues si en los primeros minutos aparecen CDSiP propios del comportamiento cardíaco enfermo, el diagnóstico quedaría unívocamente determinado.
La concepción de salud-enfermedad de los sistemas dinámicos aceptada mundialmente a partir del colloquium del 2002 (3) fue aplicada a la monitoría fetal desarrollando una reinterpretación basada en las desaceleraciones pronunciadas que son ampliamente conocidas como indicador de SFA, es decir enfermedad (22). La línea de base es un concepto adecuado a la concepción fisiológica homeostática, que esperaba la regularidad del comportamiento de la frecuencia cardíaca asociada a la salud; la teoría de los sistemas dinámicos descarta este concepto, pues demostró que era un prejuicio de la fisiología cardíaca basándose en medidas rigurosas, entre estas las realizadas en espacios de fases y otras (2,3,23-26) de la teoría del caos. Este trabajo ha confirmado que la línea de base era un prejuicio innecesario que regulariza la frecuencia cardíaca fetal y que por lo tanto no permite estudiarla desde un punto de vista matemático, físico y objetivo.
En la simplificación que se presenta para la comprensión de la dinámica cardíaca fetal, el trazado de cada prototipo es completamente diferente al de otro, lo que implica diferencias matemáticas a priori, pues con una mirada cualitativa se puede esperar diferencias en la aparición o no de todos los parámetros evaluados, lo cual se hace objetivo al hacer las mediciones, además no requiere tener en consideración las posibles enfermedades que presenten la madre o el hijo ni los estados de interés en la práctica clínica, tampoco son tomados en cuenta los factores de riesgo y es apropiada para cualquier caso con edad gestacional mayor a 28 semanas para realizar el diagnóstico, obteniendo una evaluación del estado dinámico del sistema.
Anteriormente se definieron los CDS que caracterizan diferentes eventos dinámicos y se desarrolló un análisis mediante el cálculo de probabilidades (15). Posteriormente se definieron los prototipos que generalizan el trazado de la monitoría y se calculó la probabilidad de aparición de los CDS en éstos (16). El aporte más importante de la presente investigación es la obtención de un nuevo método diagnóstico, basado en una generalización de los trabajos mencionados, capaz de evaluar matemáticamente y de manera reproducible cada trazado particular a partir de una reinterpretación de las concepciones de la física aplicadas a la fisiología.
El estudio del sistema cardiovascular ha requerido el análisis de la dinámica de diferentes variables fisiológicas con metodologías físicas y matemáticas (23-25); por ejemplo en el trabajo de Huikuri (26) se definen criterios predictores de muerte cardíaca para individuos con IAM (infarto agudo de miocardio) y fracción de eyección menor al 35 por ciento; a pesar de ser un trabajo en el que se superan las limitaciones de la evaluación diagnóstica convencional, la evaluación se desarrolla estadísticamente, de tal forma que los criterios obtenidos evalúan la población y no cada individuo particular. El presente trabajo no aplica metodologías estadísticas, pues las concepciones y análisis matemáticos utilizados proporcionan resultados diagnósticos para cada caso particular, lo que garantiza su aplicación clínica.
Según la ley de los lenguajes naturales (9-14) la dimensión fractal igual a cero indica pérdida de la complejidad de un texto y al añadir palabras en diferentes idiomas se pierde la coherencia del mismo con lo que la dimensión fractal resulta mayor a 1. En la evaluación diagnóstica aquí presentada la pérdida de complejidad es caracterizada por una dimensión fractal tendiendo a 0 o la presencia de tres o menos tipos de CDS y por ello se asocia a la enfermedad. En un texto, los valores en la dimensión fractal mayor a uno van acompañados de la pérdida de coherencia, pero en este caso se encuentran repeticiones del mismo valor en varios CDS consecutivos lo que hace que el valor de la dimensión fractal resulte mayor que uno, siendo esta una particularidad de la variabilidad observada en las frecuencias de aparición de los CDS y no necesariamente una evidencia de enfermedad.
La concepción general que guía la presente investigación es una reinterpretación de la concepción salud enfermedad basada en la teoría de los sistemas dinámicos planteada por Ary Goldberger (3); para hacerla se seleccionó un registro prácticamente lineal y otro con disminuciones pronunciadas en la frecuencia cardíaca a cambio del registro aleatorio de la concepción original; esto debido a que en la dinámica cardíaca fetal el sufrimiento fetal agudo se caracteriza por la presencia de disminuciones pronunciadas de la frecuencia y no por un comportamiento aleatorio. También se seleccionaron dos monitorías más con aceleraciones y variabilidad sin duda en su diagnóstico, asociadas a la salud. La reinterpretación descrita además de la aplicación de la ley Zipf Mandelbrot y las respectivas asociaciones con salud y enfermedad son el fundamento del diagnóstico realizado en este trabajo.
En ésta investigación, como en la física teórica desarrollada en el siglo XX (27-30), priman las relaciones de las variables independientemente de las posibles relaciones causales que se puedan postular. El presente análisis está determinado por órdenes matemáticos acausales asociados con la salud y la enfermedad basados en la experiencia clínica, por ello este es un trabajo físico y matemático de aplicación clínica. El orden temporal de los valores de la frecuencia cardíaca es impredecible, como ocurre en diferentes sistemas dinámicos (31-33) y en el caso específico del caos fetal (34) esta impredecibilidad afecta sensiblemente las evaluaciones clínicas perinatales antes o después del nacimiento. En este trabajo no se realizan contrastaciones con resultados perinatales ya que las asociaciones salud enfermedad se realizan con una metodología acausal, como fundamento teórico para resolver el problema. éstas metodologías acausales, "prejuicios teóricos", son tomados en el sentido como lo ha expresado Stev en Weinberg: "Lo importante no es estar libre de prejuicios teóricos, sino tener los prejuicios teóricos correctos" (35) buscando una metodología diagnóstica objetiva y reproducible.
Conclusiones
La metodología diagnóstica aquí presentada es útil para la diferenciación de fetos sanos y enfermos. La dimensión fractal mayor que cero de la distribución de CDS en los grupos de altura 5-10 y la suma de CDS de altura 15, 20 y 25 sea mayor que 12 y la ausencia de CDSiP se asocia a la salud. La dimensión fractal cero, ya sea en el grupo de CDS de altura 5 ó 10, o la presencia de al menos un CDSiP, o la suma de CDS de 15, 20 y 25 menor o igual que 12 o la combinación de estas medidas diagnósticas son indicadores de enfermedad.
Los cuatro prototipos fundamentales constituyen una simplificación física acausal que representa todas las posibles dinámicas cardíacas, lo cual constituye el fundamento de la metodología diagnóstica que puede ser usada con carácter preventivo.
Esta metodología es útil para cualquier caso particular y muestra que la evaluación clínica convencional podría fallar en tres de cada diez monitorías del grupo B (33,4%) y en tres de cada diez monitorías del grupo A (33,4%). La nueva metodología de diagnóstico matemático es independiente de análisis epidemiológicos.
Agradecimientos
Al grupo DHARMA que iluminó nuestro camino y el de muchos por venir. Agradecemos a todos los MAESTROS en especial al maestro Maharishi Mahesh Yogui.
Agradecemos al Instituto Colombiano para el Desarrollo de la Ciencia y la Tecnología "Francisco José de Caldas" COLCIENCIAS la financiación de este proyecto registrado con código No. 11010416380, aprobado en la convocatoria Salud 2004 por su apoyo a nuestro grupo de investigación.
Agradecemos a la Facultad de Medicina de la Universidad Nacional de Colombia Sede Bogotá, a su decano Dr. Jaime Gallego por su apoyo incondicional y a la unidad administrativa de la Facultad de Medicina por su ayuda y eficacia en los procesos institucionales necesarios para el desarrollo de esta investigación. Al Dr. Rubén Caicedo y a Ingrid Prieto por su apoyo en la concreción de los objetivos del grupo Insight.
Agradecemos al Instituto Materno Infantil, especialmente su director Dr. Odilio Méndez por su empeño en mantener el Hospital en funcionamiento y al hospital de Engativá por su aporte de monitorias.
Agradecemos a los residentes Alberto Páez y Carolina Cifuentes por su colaboración en la consecución de Historias clínicas y monitorías fetales.
Referencias
1. Devaney R. A first course in chaotic dynamical systems theory and experiments. Reading Mass.: Addison-Wesley 1992.
2. Goldberger AL, Rigney DR, West BJ. Chaos and fractals in human physiology. Sci Am 1990;262:42-9.
3. Goldberger A, Amaral L, Hausdorff J, Ivanov P, Peng C, Stanley H. Fractal dynamics in physiology: alterations with disease and aging. Proc Natl Acad Sci USA 2002 Feb; 99(suppl1): 246672.
4. Peitgen H, Jurgens H, Saupe D. Limits and self similarity. En: Chaos and Fractals: New Frontiers of Science. Springer-Verlag. New York. 1992. p.135-82.
5. Peitgen H, Jurgens H, Saupe D. Lenght, area and dimension. Measuring complexity and scalling properties. In: Chaos and Fractals: New Frontiers of Science. Springer- Verlag. New York. 1992. p.183-228.
6. Mandelbrot B. The Fractal Geometry of Nature. Freeman Ed. San Francisco, 1972, 341-348.
7. Mandelbrot B. Introducción. En: Los Objetos Fractales. Tusquets Eds S.A. Barcelona. 2000:13-26.
8. Mandelbrot B. ¿Cuánto mide la costa de Bretaña? En: Los Objetos Fractales. Tusquets Eds S.A. Barcelona. 2000:27-50.
9. Zipf GK. The human Behavior and the Principle of Least Effort. Addison-Wesley Press, Cambridge, M.A. 1949.
10. Mandelbrot B. árboles jerárquicos o de clasificación, y la dimensión. En: Los Objetos Fractales. Tusquets Eds S.A. Barcelona. 2000: 161-6.
11. Mandelbrot B. Cambios de escala y leyes potenciales sin geometría. En: La geometría fractal de la naturaleza. Freeman Ed. San Francisco, 1972: P. 477-87.
12. Burgos J. Zipf-scaling behavior in the immune system. Biosystems. 39 (1996) 227-232.
13. Burgos D. Javier. Fractal representation of the immune B cell repertoire. Biosystems. Vol 39 (1996) 19 24.
14. Rodríguez J. Comportamiento fractal del repertorio T específico contra el alergeno Poa P9. Rev Fac Med Univ Nac Colomb 2005 Apr-Jun; 53:72-8.
15. Rodríguez J, Carmona V, Avilán N, Hincapié P. Análisis de la monitoría fetal con la teoría de la probabilidad. Rev. Colomb. Obst. Gin. 2004 Dic; 55:267-78.
16. Rodríguez J, Prieto S, Avilán N, Bautista A, Ortiz L, Correa C. Caracterización matemática de la dinámica cardíaca fetal con la teoría de la probabilidad y la concepción salud enfermedad de los sistemas dinámicos. XXI Congreso Nacional de Física. Resúmenes. Vol. No. 21. 2005, p. 234.
17. Mood AM, Graybill FA, Boes D. Introduction to the theory of statistics. 3a. ed. Singapore: McGraw-Hill; 1974.
18. Benson R. Diagnóstico y tratamiento ginecoobstétrico. 4 ed. México DF: El Manual Moderno SA de CV; 1986.
19. Sánchez F. Alto riesgo obstétrico. Bogotá: Universidad Nacional de Colombia; 1988.
20. Pritchard JA, MacDonald PC, Gant NF (eds). Williams Obstetricia. Barcelona: Salvat Editores; 1986.
21. Borgatta L, Shrout PE, Divon MY. Reliability and reproducibility of nonstress test readings. Am J Obstet Gynecol 1988;159: 554-8.
22. Nacional Institute of Child Health and Human Development (NICHD) Research Planning Workshop. Am J Obstet Gynecol. 1997 Dec; 177: 138590.
23. Goldberger AL, West BJ. Fractals in physiology and medicine. Yale J Biol Med 1987; 60: 421 35.
24. Goldberger A. Nonlinear dynamics for clinicians: chaos, theory, fractals, and complexity at the bedside. Lancet 1996; 347: 13124.
25. Lipsitz LA, Goldberger AL. Loss of «complexity» and aging. Potential applications of fractals and chaos theory to senescence. JAMA 1992; 267:1806-9.
26. Huikuri H, Mäkikallio T, Peng C, Goldberger A, Hintze U, Moller M. Fractal correlation properties of R R interval dynamics and mortality in patients with depressed left ventricular fuction after an acute myocardial infarction. Circulation 2000 Jan; 4 (11): 4753.
27. Feynman R. Los principios de la mecanica estadistica. En: Física. Vol 1, Cap 40. Addison Wesley Iberoamericana S.A. 1987.
28. Feynman R. Comportamiento cuántico. En: Física. Vol 1, Cap 37. Addison Wesley Iberoamericana S.A. 1987.
29. Fernández-Rañada A. Movimiento caótico. En: Orden y Caos. Scientific American. Prensa Científica S.A.; 1990. p. 66, 77.
30. Crutchfield J, Farmer D, Packard N, Shaw R. Caos. En: Orden y Caos. Scientific American. Prensa Científica S.A.; 1990. p. 78-90.
31. Procaccia I. Universal properties of dynamically complex systems: the organization of chaos. Nature 1988 Jun 16; 333: 618-23.
32. Kloeden PE, Mees AI. Chaotic Phenomena. Bulletin of Mathematical Biology 1985; 47(6): 697-738.
33. Denton T, Diamond G, et al. Fascinating rhythm: A primer on chaos theory and its application to cardiology. Am Heart J 1990; 6 (1): 1419-40.
34. Gough N. Fractals, chaos, and fetal heart rate. Lancet 1992 Jan 18; 339: 1823.
35. Weinberg S. Los tres primeros minutos del Universo. 3ª. Edición. Madrid: Alianza, 1980, p 105.