Thiel, Christian (ed.). Leopold Löwenheim (1878-1957).

Thiel, Christian (ed.) Leopold Löwenheim (1878-1957). Edición especial de la revista History and Philosophy of Logic XXVIII/4 (2008).

RESEÑA

Thiel, Christian (ed.)
Leopold Löwenheim (1878-1957).
Edición especial de la revista
History and Philosophy of Logic XXVIII/4 (2008).

---

Para aquellas personas no emparentadas con la lógica matemática, el nombre Leopold Lowenheim puede resultar curioso y hasta gracioso; además de encontrar problemática su correcta pronunciación. Más allá de esto, ese nombre refiere a un alemán hijo del matrimonio entre un profesor de matemáticas, Detmold Louis Lowenheim, y una escritora, Elise Rohn, nacido el 26 de junio de 1878 en Krefeld, una pequeña ciudad al noroeste de Dusseldorf, cuyas contribuciones al algebra de la lógica y a la hoy denominada "teoría de modelos" han resultado de capital importancia.

La revista History and Philosophy of Logic le dedicó este número en ocasión de los 50 años de su muerte. El editor invitado a cargo de esta edición especial fue Christian Thiel, renombrado filosofo de las matemáticas y estudioso de la obra de Gottlob Frege, cuyo artículo "A Short Introduction to Lowenheim's Life and Work and to a Hitherto Unknown Paper" brinda un panorama sucinto de la vida y obra del alemán. Esta edición también incluye cinco fotografías, y la bibliografía detallada de todos los escritos de Lowenheim, así como de las publicaciones de sus padres.

Lowenheim siguió sus estudios universitarios en matemáticas y ciencias naturales en la Universidad Federico- Guillermo (hoy Universidad Humboldt de Berlin) y en la Escuela Técnica Superior en Charlottenburg. Su vida profesional transcurrió como profesor de matemáticas y física en diversos colegios de Berlin. A pesar de que este ambiente no le proveía de un contexto académico idóneo para desarrollar sus trabajos en lógica matemática, Lowenheim logro llevar a cabo investigaciones en el campo del algebra de la lógica y publico sus mayores contribuciones entre 1908 y 1919. Fue, así mismo, un consagrado miembro de la Sociedad Matemática de Berlín; publico en revistas de alto prestigio internacional, y mantenía correspondencia con los (lógico-) matemáticos más destacados de su época: Bernays, Hilbert, Frege, Zermelo y Muller, por mencionar algunos.

En cuanto a sus trabajos en lógica, estos "no resultan accesibles al lector contemporáneo, debido, por un lado, a la distancia histórica del tema en cuestión y, por el otro, a su preferencia por la obsoleta notación de Schroder-Peirce" (294). Hoy su nombre no puede dejar de asociarse al conocido "Teorema de Lowenheim-Skolem", cuya formulación contemporánea equivalente es la siguiente:

f es satisfacible → (f es satisfacible finitamente ∨ f es 0-satisfacible)

La repercusión de este resultado, que para Lowenheim pasó inadvertido, estriba en mostrar la existencia de modelos numerables de una teoría de primer orden que pretenda caracterizar un dominio no-numerable. Esto significa que a una teoría de primer orden f sobre infinitos incontables (o no-numerables) como los números reales -esto es, cuya cardinalidad exceda la de los números naturales, sea mayor que 0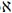- también se le puede encontrar un modelo cuyo dominio sea solo contable. Por tanto, la importancia está en advertir que sistemas que hablen sobre infinitos incontables también pueden ser interpretados como si se tratase de un conjunto de objetos no mayor al de los números naturales.

Ahora bien, lo relevante de esta edición es la publicación póstuma de un artículo que Lowenheim, presumiblemente, escribió alrededor de 1935: "Funktionalgleichungen im Gebietekalkul und Umformungsmoglichkeiten im Relativkalkul" [Ecuaciones funcionales en el cálculo de campos y posibilidades de transformación en el cálculo de relativos], cuyo análisis y evaluación pormenorizada, como afirma Thiel, "permanece como una tarea para los historiadores de la logica, en particular los que estudian el algebra de la lógica post-Schroderiana" (298). Esta última contribución técnica de Lowenheim iba a ser publicada en la prestigiosa revista polaca Fundamenta Mathematicae en 1939, pero a causa de la invasión de tropas alemanas en Polonia permaneció inédita hasta hoy. El artículo se divide en dos partes. En la primera, Lowenheim retoma sus investigaciones de 1910 y 1913 en torno a los múltiples métodos de encontrar soluciones reproductivas en las ecuaciones funcionales de Boole partiendo de soluciones particulares. La segunda parte es una continuación del seminal artículo "Uber Moglichkeiten im Relativkalkul" [Sobre las posibilidades en el cálculo de relativos], y se aboca principalmente al problema de los limites de la eliminación.

En resumen, esta edición de lujo conmemora a uno de los lógicos mas importantes del siglo pasado, y es mi deseo personal que, gracias a este tipo de publicaciones, lo que de un tiempo a esta parte se ha llamado "a neglected chapter in the history of logic" -frase acuñada por Geraldine Brady- reciba la atención debida, pues las contribuciones de este periodo han sido y son de gran importancia para los actuales desarrollos de la lógica.

---

Bibliografía

Lowenheim, L. "Uber Moglichkeiten im Relativkalkul" [Sobre las posibilidades en el calculo de relativos], Mathematische Annalen 76 (1915): 447-470.

---

ALONSO ZELA
Universidad de Buenos Aires-Argentina
alonso.zela@uba.filo.ar