ANÁLISIS DE EXCAVACIONES EN LA MINA SUBTERRÁNEA EL TORO POR MEDIO DE ELEMENTOS FINITOS
ANÁLISIS DE EXCAVACIONES EN LA MINA SUBTERRÁNEA EL TORO POR MEDIO DE ELEMENTOS FINITOS
FINITE ELEMENTS ANALYSIS FOR UNDERGROUND OPENINGS AT EL TORO MINE.
ÁLVARO J. CASTRO CAICEDO.
Ingeniero de Minas M. Sc. Universidad Nacional de Colombia, Medellín,ajcastro@unal.edu.co
JUAN E. MONSALVE OLIVEROS.
Ingeniero de Minas y Metalurgia. Planta El Cairo. Cementos Argos S. A. jmonsalve@grupoargos.com
Recibido para evaluación: 22 de Marzo de 2007 / Aceptación: 09 de Noviembre de 2007 / Recibida versión final: 14 de Noviembre de 2007
RESUMEN
En la mina subterránea El Toro se explota roca calcárea para la fabricación de cemento en la Planta El Cairo, de Cementos Argos S. A. El método de explotación es conocido como realce por subniveles o sublevel stoping, que consiste en la abertura de cámaras mediante perforación y voladura con explosivos, cada cámara excavada tiene dimensiones de 20m de ancho, 45m de altura y longitudes entre 80 y 120 m, separadas por pilares intermedios de 10 m de espesor, definiendo conjuntos denominados Bloques de explotación.
Este artículo presenta el proceso realizado con el fin de modelar y evaluar la distribución de los desplazamientos y de los esfuerzos resultantes de la compleja interacción de los Bloques de explotación. La modelación numérica se realizó con fundamento en la mecánica del medio continuo y por medio de la técnica de los elementos finitos; inicialmente se obtuvo el modelo geomecánico del terreno rocoso y posteriormente el modelo numérico incluyendo las excavaciones. Se evaluaron varias configuraciones geométricas de los Bloques de explotación proyectados, y se concluyó con una propuesta de diseño que ofrece estabilidad del terreno intervenido y permite extraer el mayor volumen posible de reservas minerales.
PALABRAS CLAVE: Minería Subterránea, Realce por Subniveles, Mina El Toro, Elementos Finitos, Ansys, Argos, Caliza, Criterio Hoek-Brown.
ABSTRACT
El Toro underground mine is located at Antioquia, Colombia and exploits a limestone deposit through sublevel stopping mining method. The mine was designed with five exploitation levels with 65m high, 20m wide and 120 m long stopes sets.
In this work is presented the process to obtain the assessment of the mechanical behavior of the rock mass under stoping effects, the geomechanical and numerical models were obtained and several stopes configurations were evaluated including existing and projected openings. The work concludes with geometrical modification that besides to offer stability of ground, allows to extract greater volume of mineral reserves.
KEY WORDS: Underground Mining, Sublevel Stoping, El Toro Mine, Geomechanics, Finite Elements, Anys, Argos, Sublevel Stoping, Limestone, Hoek-Brown Criteria.
1. INTRODUCCIÓN
La mina El Toro inició la extracción de caliza cementera por métodos de superficie en la década de 1950, en 1995 fue necesaria la transición para minería subterránea. El yacimiento se encuentra en el Municipio de Abejorral, a 70 Km de Medellín, enmarcado en el complejo polimetamórfico de la Cordillera Central. Las rocas presentes son fundamentalmente esquistos cuarzo-sericíticos, esquistos verdes y mármol. El cuerpo calcáreo explotado presenta actitud promedio N-S 20º/60º 10ºW, tiene unos 800 m de longitud en el rumbo, 120 m de potencia en promedio y según Tobón y Monsalve (2001) se ha comprobado en una profundidad hasta de 600 m desde bocamina en superficie.
El proyecto de ingeniería de minas inicial definió tres niveles de explotación, posteriormente se proyectaron dos niveles a mayor profundidad que los iniciales. El presente estudio intentará analizar desde la geomecánica las posibilidades de explotación de los bloques inferiores bajo la interacción de los bloques existentes superiores, pues es de alta importancia evaluar las condiciones de estabilidad mecánica del terreno intervenido, más si considerando que es compleja la interacción de excavaciones de grandes dimensiones, tanto en términos de esfuerzos como de desplazamientos. Para la evaluación de la estabilidad de excavaciones subterráneas son diversas las técnicas factibles de aplicar; quizás las que tienen mayor aceptación son aquellas fundamentadas en el monitoreo de los desplazamientos y de los esfuerzos pues provienen de lecturas directas.
En el medio nacional, pocas han sido las aplicaciones de las técnicas numéricas en el modelamiento minero, el método de los elementos finitos aquí utilizado es fundamentado en la mecánica de los medios continuos, y ofrece posibilidades complementarias con relación a aquellas de los registros directos puntuales, pues considera las propiedades mecánicas del macizo rocoso por medio de leyes constitutivas definidas para el terreno. En nivel internacional, y para casos semejantes al que aquí se trata, son recomendadas más que técnicas únicas, la integración de diversas estrategias, entre ellas: el monitoreo en campo, las pruebas de laboratorio, los modelos matemáticos y últimamente, las simulaciones numéricas, a las que pertenece la técnica de elementos finitos que aquí se propone.
El proceso para el diseño de las excavaciones mediante modelamiento numérico seguido en este trabajo es presentado en el diagrama de la Figura 1.
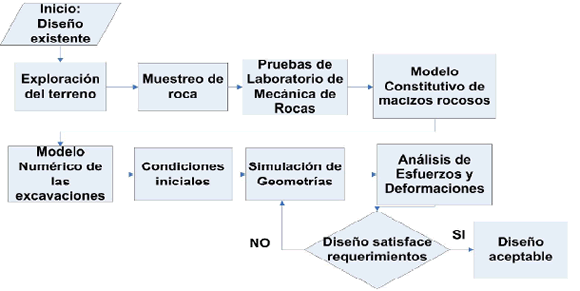
Figura
1. Operaciones
para el modelamiento numérico de excavaciones en medios rocosos.
2. EL PROYECTO MINERO
En la Mina el Toro se proyectaron cinco Bloques de explotación que se presentan de forma esquemática en la Figura 2. En cada Bloque se desarrollaron conjuntos de cámaras paralelas, mediante el método de explotación conocido como sublevel stoping. En el momento de este estudio los Bloques Geominas y 1 se encuentran explotados, el Bloque 2 está próximo a agotarse y están en desarrollo los accesos a los Bloques 3 y 4, en cuyo diseño geométrico se centra este trabajo.
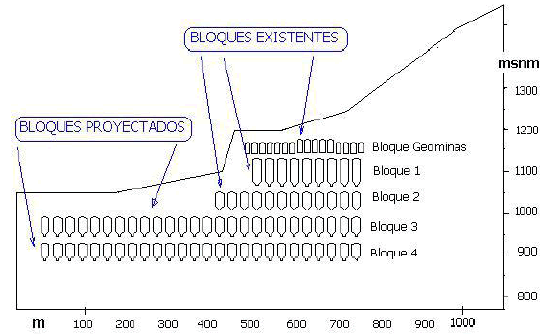
Figura
2. Sección
transversal vertical esquemática de las excavaciones en la Mina el Toro.
En el método de sublevel stoping, cada Bloque es separado por pilares corona horizontales a modo de losa, con 16 m de espesor. El método de explotación consiste en excavar cámaras perpendiculares al rumbo del cuerpo mineral, conformando cavernas de 20 m de luz, 45 m de altura y longitudes entre 80 y 120 m, dependiendo de la potencia del yacimiento, que son separadas por pilares verticales de 10 m de espesor, en una recuperación media del 54% de las reservas (Tobón y Monsalve, 2001). Las vías de desarrollo y preparación corresponden a túneles, guías y cruzadas. En la Figura 3 se presenta el aspecto de una cámara de explotación típica.
En el diseño del método de explotación se ha aprovechado la calidad autoportante del macizo rocoso. Sin embargo, las grandes dimensiones excavadas y el grado de fracturamiento de la roca exigen prevenir el desprendimiento de bloques y los desplazamientos, por lo cual se instalan cables de acero que atraviesan transversalmente los pilares. Un ejemplo de esta fortificación es mostrada en la Figura 4.

Figura
3. Cámara de explotación en el Boque 2, dimensiones: altura 45m, ancho 20m, longitud 120m. Fuente:
Cementos El Cairo, Informe social 2003.
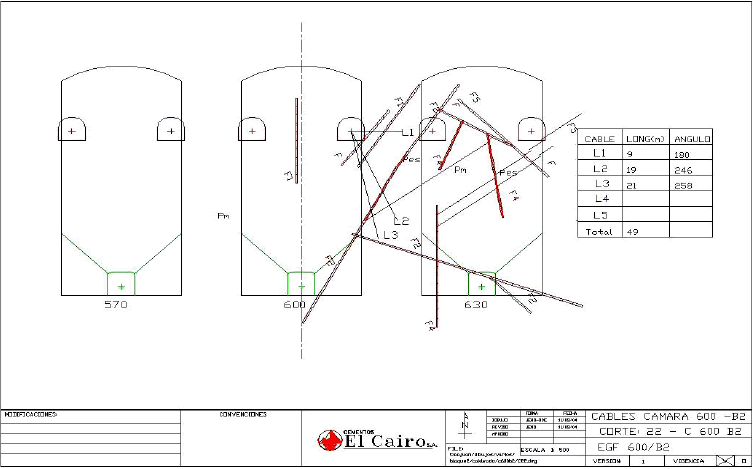
Figura
4. Fortificación
mediante cables en pilares de cámaras. 3.
CARACTERIZACIÓN EN LABORATORIO DE MECÁNICA DE ROCAS
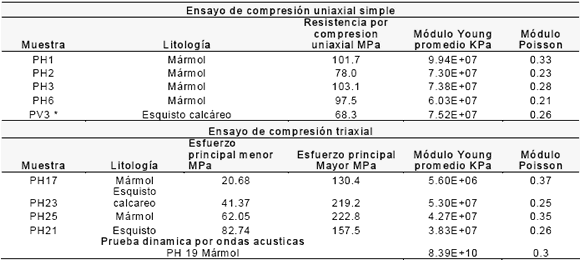
Las muestras para pruebas de laboratorio de diferentes sectores del cuerpo calcáreo y de la roca circundante fueron obtenidas mediante sondeos realizados desde las labores subterráneas. Las pruebas sobre núcleos fueron realizadas en el Laboratorio de Mecánica de Rocas de ICP-ECOPETROL siguiendo las normas ASTM, los resultados principales se presentan en la Tabla 1. El comportamiento esfuerzo-deformación de las probetas fue típicamente característico de roca frágil, evidenciada por la disminución inicial de la deformación volumétrica y por su posterior aumento después de un nivel de esfuerzos dado (<biblio>), en la Figura 5 se muestra el caso del mármol.
Tabla
1.
Resultados de las pruebas de mecánica de rocas. Fuente: ICP-ECOPETROL,
2005.
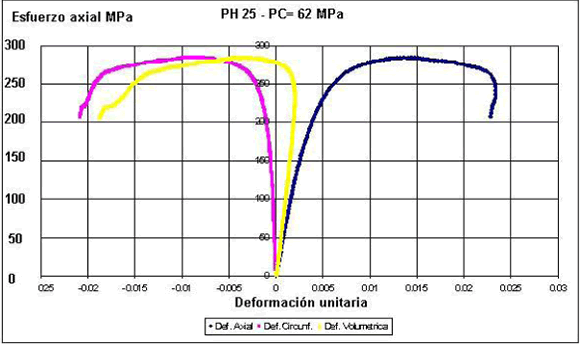
Figura
5. Relación
del esfuerzo axial con las deformaciones unitarias en prueba triaxial de muestra
de mármol.
Sobre el esquisto se debe resaltar que estudios como el de Nasseri et al. (2003) demuestran la importancia de la orientación de la esquistosidad, que confiere a la roca una marcada anisotropía mecánica. En el caso del estudio, no fueron realizadas pruebas considerando este efecto pues los pilares y cámaras son constituidos fundamentalmente por roca calcárea.
4. LOS ESFUERZOS IN SITUNo se ha realizado medición del tensor de esfuerzos en el terreno, constituyendo una limitación de los modelos geomecánico y numérico. Debido a esto, en el análisis numérico se consideraron únicamente fuerzas de cuerpo, en el cual la densidad del material define la magnitud del esfuerzo de acuerdo con la localización del punto. Así, el esfuerzo máximo en la cota base del Bloque 4 con un peso específico de 2.71 t/m3 correspondería a un esfuerzo vertical de 10.84 MPa. De otra parte, a partir de estudios de microtectónica de Gil (1996) en los distritos de Montebello y Abejorral, se encontraron las direcciones de los esfuerzos mayores; se dice que en los últimos 10 millones de años ha sido de N45°W, es decir en dirección aproximadamente perpendicular al eje longitudinal de las cámaras de explotación, teóricamente la peor orientación para la estabilidad de las cámaras. Sobre el esfuerzo horizontal, se asume que puede tener magnitud entre 1.25 y 1.5 la magnitud del esfuerzo litostático vertical, correspondiendo entre entre 13.55 y 16.26 MPa.
5. MODELOS CONSTITUTIVOS PARA ROCAS
Los modelos constitutivos para rocas, incluyendo tanto los macizos rocosos como las discontinuidades, son los componentes más importantes en las soluciones numéricas en los problemas prácticos de la ingeniería y uno de los temas más investigados en la mecánica de rocas. En el caso de la mina El Toro, y para la modelación geomecánica y numérica se utilizarán los modelos clásicos basados en las teorías de la elasticidad y de la plasticidad, con consideración de los efectos de las fracturas, de la meteorización de las rocas y del efecto de las voladuras sobre el macizo. El modelo elástico lineal basado en la ley de Hooke sigue siendo el comportamiento mecánico más adoptado, especialmente para rocas duras (Jing, 2003), como es el caso tratado. La ley constitutiva es caracterizada por los módulos de Young, de Poisson, de Corte y de Deformación por corte. Modelos más sofisticados para elasticidad anisotrópica pueden ser obtenidos por formas cerradas considerando condiciones de simetría elástica para roca intacta, tal como elasticidad isotrópica transversal, o de continuo elástico intersecado por fracturas.
Los modelos plásticos y elasto-plásticos han sido ampliamente desarrollados y aplicados en rocas fracturados desde 1970, con los criterios de falla de Mohr-Coulomb y Hoek-Brown (Hoek, Brown, 1997) usados como funciones de cedencia y de potencial plástico.
Los modelos de endurecimiento por deformación (strain-hardening) y de ablandamiento por deformación (strain-softening) son los comportamientos plásticos más utilizados, siendo el segundo más comúnmente observado en pruebas de compresión uniaxial. Es de anotar aquí que debido a las características del equipo de laboratorio no fue posible realizar la prueba esfuerzo-deformación en condición post falla, sin embargo los resultados del informe permiten observar una tendencia hacia el comportamiento elástico-frágil en el mármol y también en el esquisto, para el rango de esfuerzos de trabajo propuesto en la sección anterior.
El criterio de Hoek-Brown para macizos rocosos
Cuando se usan modelos numéricos con la intención de estudiar la ruptura progresiva de macizos rocosos, los criterios de falla son aplicados como un criterio de cedencia de superficies y el análisis se hace por teoría de plasticidad. Los criterios más usados en rocas han sido los de Mohr-Coulomb y de Hoek-Brown.
En este estudio se aplicó el criterio generalizado de Hoek-Brown para macizos rocosos versión 2002, el cual busca describir el comportamiento de terrenos atendiendo condiciones para el diseño de excavaciones subterráneas de difícil inserción en los modelos analíticos cerrados, tales como la presencia y rugosidad de fracturas, de materiales heterogéneos por meteorización diferencial y de diaclasas con relleno. Condiciones todas que afectan considerablemente la estabilidad de las excavaciones. El criterio Hok-Brown ha demostrado cierta confiabilidad para definir las condiciones de esfuerzos bajo las cuales el macizo deformará inelásticamente, o colapsará, si la excavación no es adecuadamente soportada. Las propiedades del macizo rocoso fueron obtenidas de observaciones in situ.
El criterio Hoek-Brown para muestras intactas describe la relación no lineal entre el esfuerzo axial máximo que es soportado por la muestra (σ1), y el esfuerzo de confinamiento (σ3) por medio del parámetro mi (Carranza-Torres, Fairhurst, 1999. Hoek E. 2001). Para evaluar la resistencia del macizo in situ es aplicado el factor GSI (Geological Strength Index), a través de la evaluación de las discontinuidades y la meteorización, varía entre 10 (muy mala calidad) y 100 (excelente calidad), y que puede ser estimado por examen del macizo. Los resultados se presentan en la Tabla 2.
Tabla
2. Parámetros del criterio Hoek-Brown del macizo calcáreo en el área de la Mina El
Toro.
Los parámetros GSI, mi, mb, s y a evalúan las condiciones de meteorización, de las discontinuidades y la resistencia triaxial del macizo rocoso. Los resultados del criterio permitirían considerar el macizo rocoso en grado medio, según el mismo criterio. Según Hoek (2001) esta clase de macizos tienden a tener deformación post-falla con reducción de la resistencia del estado in situ al estado fracturado que se supone sucede en un nivel de esfuerzos constante, definida por la resistencia por compresión del macizo fallado.
6. MODELO NUMÉRICO DE LAS EXCAVACIONES
Los métodos numéricos más comunes en mecánica de rocas en el caso del medio continuo son los de diferencias finitas, elementos finitos y de elementos de contorno; y en el medio discontinuo son los llamados de elementos discretos y de red de fracturas discretas.
El método de los elementos finitos requiere la división del dominio del problema en un conjunto de sub-dominios (elementos) de pequeño tamaño y geometría estándar (triangulares, cuadriláteros, tetraedros, etc) con un número fijo de nodos en el vértice y/o lados. Para aproximar el comportamiento de los nodos en los elementos son usadas funciones polinomiales y así generar las ecuaciones que representan el comportamiento de los elementos. Después, con la imposición de condiciones iniciales y de frontera apropiadas, las ecuaciones elementales son ensambladas de acuerdo con relaciones topológicas entre nodos y elementos en un sistema global de ecuaciones algebraicas cuya solución produce la información requerida en el dominio.
En cuanto al tipo de material, se utilizó el tipo Drucker-Prager, donde los parámetros de cohesión y de fricción definen su comportamiento. En relación con la deformación plástica, el potencial de dilatación de la roca fue controlado por el ángulo de dilatancia; si este ángulo es igual al de fricción, la ley de flujo es asociativa y la roca aumenta de volumen mientras se deforma, si el ángulo de dilatancia es cero o menor que el de fricción, el material no aumenta de volumen mientras hay fluencia y se dice que la ley de flujo es no asociativa (hipótesis conservadora). El modelo numérico aplicó comportamiento elástico perfectamente plástico y con regla de flujo no asociativa, la simulación será por tanto conservadora, pues además considera únicamente los esfuerzos litostáticos. Geométricamente se tomó como plano de análisis una sección vertical transversal a las cámaras de explotación y en la cual se recogió el perfil del relieve.
Una vez disponible la información obtenida en los apartes anteriores, el proceso de modelamiento numérico debe seguir una serie de etapas. Según Moaveni (1999) las etapas básicas en cualquier proceso de análisis por elementos finitos son:
Este proceso se realizó mediante el software ANSYS con licencia adquirida por la Universidad Nacional. el elemento de análisis es conformado por ocho nodos con dos grados de libertad en cada uno de ellos, mostrado en la Figura 6, que son las translaciones en las dos direcciones coordenadas x (horizontal) y y (vertical), el cual es usado para modelar estructuras sólidas, bajo esfuerzo plano ó deformación plana. Este elemento puede deformarse plásticamente, por creep, por escurrimiento (swelling), endurecimiento por esfuerzos (stress stiffening), y es adecuado para reflejar grandes deformaciones.
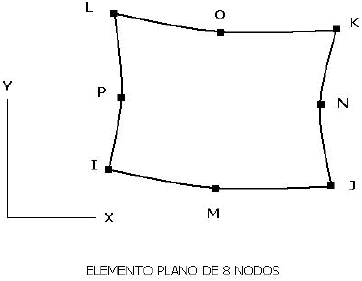
Figura
6. Representación
del elemento bidimensional rectangular utilizado para el
modelamiento.
Las deformaciones principales son calculadas de las componentes de deformaciones mediante la ecuación:
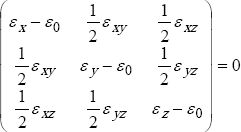
Donde: εo = deformación principal (3 valores)
Las tres deformaciones principales son denominadas ε1, ε2, y ε3 y son ordenadas de forma que ε1 es la mayor positiva y ε3 es la mayor negativa (salida como EPEL 1, 2, y 3).
La intensidad de deformación εI (salida como INT EPEL) es el mayor de los valores absolutos de ε1 - ε2, ε2 - ε3, ó ε3 - ε1. es:
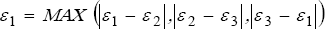
La deformación equivalente Von Mises εe (salida como EQV) es calculada por:
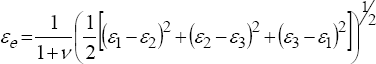
Donde v es el Coeficiente de Poisson.
Los esfuerzos principales (σ1, σ2, σ3) son calculados a partir de las componentes por la ecuación cúbica:
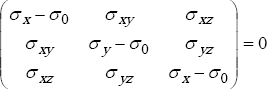
Donde: σo = esfuerzo principal (3 valores)
Los esfuerzos principales son σ1, σ2, y σ3 (salidas como S1, S2, y S3). Los esfuerzos principales son ordenados de forma que σ1 es el mayor positivo (tracción) y σ3 es el mayor negativo (compresión).
La intensidad de esfuerzos σI (salida como SINT) es el mayor de los valores absolutos de σ1-σ2, σ2-σ3, ó σ3-σ1. Es decir:
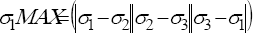
El esfuerzo equivalente de Von Mises σe (salida como SEQV) es calculado como:
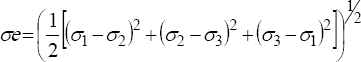
El esfuerzo equivalente es relacionado con la deformación equivalente por
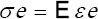
Donde E = Módulo de Young
Se obtuvieron los modelos de los niveles de esfuerzos y deformación presentados a seguir.
7. ANÁLISIS DE RESULTADOS
Inicialmente, y debido a la presencia de excavaciones al momento de realizar las simulaciones, es necesario incluir su efecto sobre el modelo numérico, es decir no existe estado inicial de equilibrio. Para ello se utilizan los valores de desplazamientos medidos en el monitoreo. Las restricciones son de movimiento horizontal en los bordes verticales laterales y de movimiento vertical y horizontal en la superficie de base, por lo cual la interpretación más confiable es en las proximidades de las cámaras.
SIMULACIÓN 1
Se modela el comportamiento del terreno al momento de finalizar las excavaciones de los Bloques Geominas, 1 y 2, con las dimensiones existentes, es decir, claro de cámaras de 20 m, altura de 45 m y ancho de pilar de 10 m, con espesor de losa entre niveles de 16m. En la Figura 7 Figura 7 se presenta el resultado para los desplazamientos totales.
Figura
7. Modelo de desplazamientos totales (m). La escala gráfica permite observar la
intensidad y tendencia del movimiento del terreno por
gravedad.
Los desplazamiento en los puntos registrado por los extensómetros en la parte baja y media de los pilares de los Boques 1 y 2 es aproximada a la mostrada en la Figura 6, se observa que en los techos de las cámaras sur (derecha), se calculan desplazamientos totales hasta de 0,29 m, los extensómetros han registrado hasta el momento hasta 0,02 m. Las cámaras del Bloque 1 también presentan desplazamientos comparables con Bloque 2.
Las regiones topográficamente elevadas presentan tendencia a continuar el movimiento descendente. Este movimiento puede acelerarse por procesos como infiltración de aguas de escorrentía y degradación superficial o con los movimientos en superficie ya existentes y relacionados con la explotación de cielo abierto.
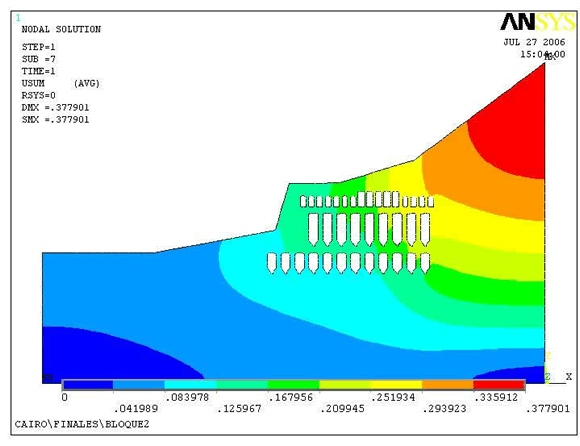
En relación con los esfuerzos, en la Figura 8 es visible que la mayor parte del Bloque 2 soporta esfuerzos máximos de 1,3 a 2,8 MPa los cuales actúan sobre las bóvedas en los Bloques superiores. Los pilares están en tracción en su parte media interna y en la base tipo zapata, comportamiento que pasa a compresión en la losa entre Niveles, exceptuando las zonas de borde donde se presenta generalmente tracción. Los techos en bóveda pueden manifestar concentración de esfuerzos de tracción, hecho de importancia para su estabilidad.
Figura
8. Modelo visto en detalle y magnitudes de
esfuerzo principal mayor en los Bloque 1 y 2 (Newtons/m2).
SIMULACION 2
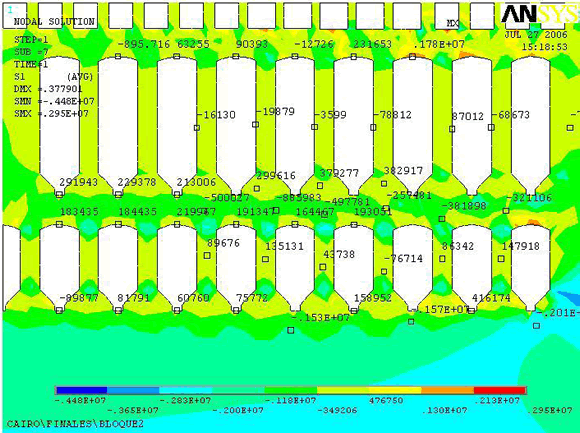
En la Figura 9 se modela el comportamiento del terreno al momento de finalizar las excavaciones de los Bloques Geominas, 1, 2, 3 y 4 para las dimensiones de proyecto original, como en la simulación 1.
Figura
9. Modelo de desplazamientos totales (m) en la finalización
de excavaciones de los Bloques proyectados.
En los bloques 2, 3 y 4 predominan desplazamientos desde 0 hasta 0.32 m, siendo notable el aumento del área desplazada en grado máximo en el Bloque 1, es decir, las regiones topográficamente elevadas presentan tendencia a continuar el movimiento descendente.
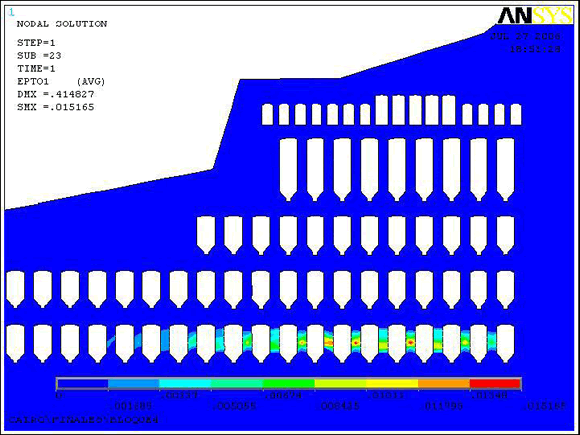
Figura
10. Modelo de la deformación unitaria total
mayor.
En la Figura 10 se observa que la deformación unitaria máxima se concentrará en los pilares del bloque inferior hasta de 0.0015m/m. por lo cual se considera recomendable continuar reforzando los pilares con los cables.
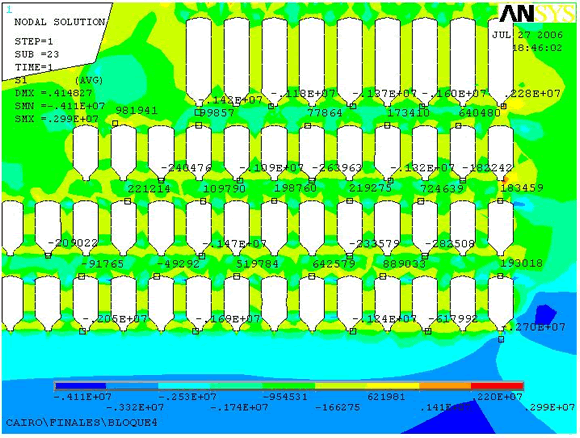
Figura
11. Modelo del esfuerzo principal mayor
(N/m2).
En la Figura 11 se observa que la magnitud del esfuerzo principal mayor se modifica con respecto a las simulaciones anteriores, alcanzando máximos de 2,9 Mpa. Al finalizar el Bloque 3 la nueva geometría excavada reduce los esfuerzos por la redistribución de los mismos. Los pilares continúan en tracción en su sección media y compresión continua hasta la losa entre bloques. Los contornos de las bóvedas alcanzan tracción hasta de 0,9 MPa en todos los Bloques pero también se presentan algunas bajo compresión en el Bloque 4. Las zonas de las cruzadas se encuentran en compresión hasta de 2,7 MPa.
SIMULACIÓN 3
En este modelo se simulan los bloques de explotación modificando las dimensiones originales de proyecto, se evalúan cámaras de claro de 35 m y ancho de pilares de 12 m, las restantes dimensiones se conservan como en las simulaciones anteriores. En la Figura 12 se observan los resultados, estas dimensiones no son estables para la mina.
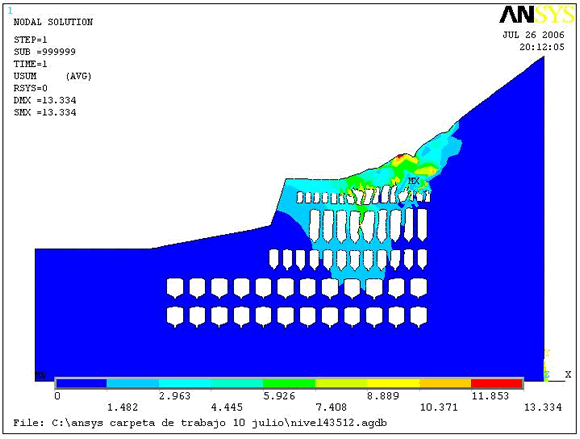
Figura
12. Modelo no estable por desplazamientos totales.
En la simulación 3 se observa que se forman zonas de colapso en los Bloques superiores que conllevan subsidencia en superficie, en estos puntos los desplazamientos totales alcanzarían los 13,3 m. La simulación bajo estas dimensiones no es estable.
SIMULACIÓN 4
Se modifican las dimensiones del proyecto original, se evalúan los Bloques 3 y 4 con cámaras con ancho de 45 m y ancho de pilares de 15m, el espesor de la losa se mantiene en 16 m.
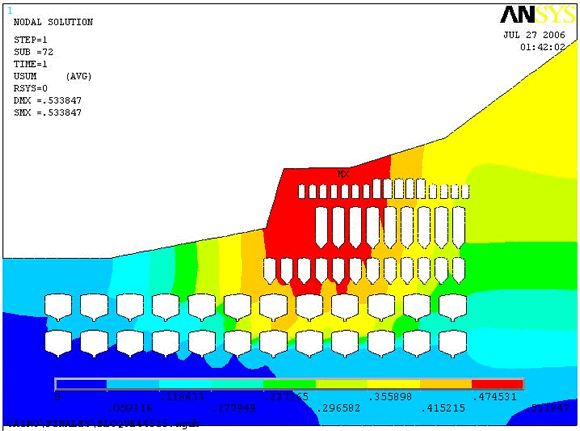
Figura
13. Modelo
de desplazamiento totales (m) para modificaciones de ancho de cámaras y pilares
en los Bloques 3 y 4.
En la Figura 13 los valores máximos en color rojo se sitúan en la zona central de los Bloques superiores, con valores hasta de 0,53 m. La estabilidad deberá ser evaluada mediante las deformaciones totales, elásticas y plásticas, como presentado en la Figura 14.
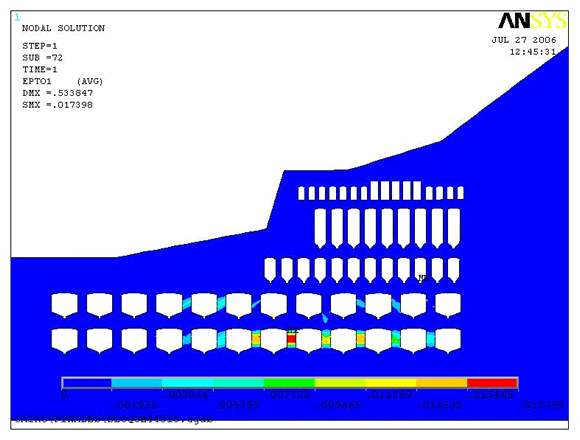
Figura
14. Modelo de deformación unitaria principal mayor elástica y
plástica.
En el modelo de la Figura 14 es visible que el valor máximo en el pilar central del Bloque 4 es de 0,017 m/m que corresponde a 0,25 m pero gran parte de los Bloques presentaría valores menores a 0,05 m. El valor máximo de la deformación unitaria plástica bajo este diseño es de 0,016 m/m en el mismo pilar, por lo tanto la deformación elástica corresponde sólo a 0,001 m/m de la total. En la Figura 15 se presenta el modelo de la dirección de las deformaciones totales, la mayor en color negro y la menor en azul. Es visible la orientación de la deformación máxima en dirección horizontal y mínima en la vertical en algunos pilares del Bloque 4.
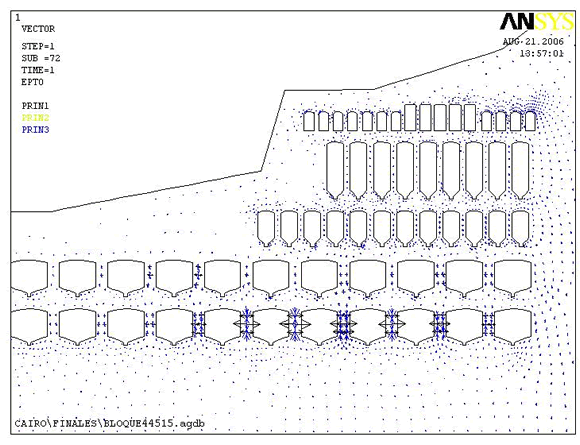
Figura
15. Dirección de las deformaciones unitarias principales totales (elásticas y
plásticas).
En la Figura 16 se observa la distribución del esfuerzo principal mayor para la simulación 4, se observa que se mantienen los pilares en tracción a media altura y hacia el contorno excavado, hacia el centro de la losa se definen zonas de compresión. Se concentran esfuerzos en las bóvedas de los pilares hasta de 3,9 MPa en tracción, en áreas comparativamente pequeñas en relación con sus dimensiones.
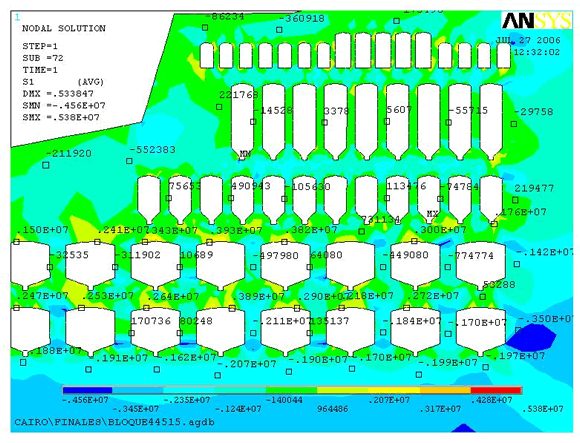
Figura
16. Modelo de esfuerzo principal mayor (N/m2).
DISCUSIÓN Y CONCLUSIONES
La modelación mediante métodos numéricos es un proceso metódico que demanda recursos técnicos, económicos y de personal especializado, factores que posiblemente han incidido en su baja aplicación en la minería colombiana. Sin embargo, sus resultados son satisfactorios siempre que dicho proceso sea conducido con adecuado criterio, proveniente del conocimiento del problema en campo. Algunos de los aspectos fundamentales encontrados en el caso de la Mina El Toro son discutidos a continuación.
La calibración del modelo numérico inicial es fundamental, en este caso se hizo considerando el momento final de las excavaciones de los Bloque Geominas, 1 y 2; en este momento se concluye que las condiciones de estabilidad son altas, existen muy pocos sectores bajo estado plástico. Los esfuerzos máximos son alrededor de 11,8 MPa en algunos pilares.
En el Bloque 1 con dimensiones de 65 m alto, 20 m ancho y 10 m ancho de pilar, los extensómetros han registrado hasta el momento desplazamientos totales hasta de 0,02 m; según el modelo numérico y una vez totalmente excavados los Bloques 3 y 4, los desplazamientos alcanzarían hasta 0,41m. Debe recordarse que en el terreno se realiza refuerzo mediante cables que no fue considerado en el modelo numérico.
Otro resultado importante es la optimización de las dimensiones relativas de cámaras y pilares, considerando como base el diseño de 20m por 10m de ancho respectivamente, el factor de recuperación de reservas es del 66%, una comparación de este importante parámetro económico se presenta en la Tabla 3.
Tabla
3. Factor de recuperación de reservas para diferentes dimensiones de cámaras y
pilares en la mina el Toro.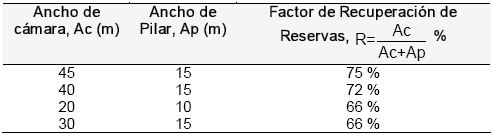
La modelación al finalizar los Bloques 1, 2, 3 y 4 muestra que la opción de cámaras con luces de 45 m y pilares de 15 m posibilita aumentar la recuperación de reservas en un 9%, con un significativo aumento de la vida de la mina, esto manteniendo las alturas constantes. Gracias a la calidad del macizo rocoso, las magnitudes de esfuerzos y desplazamientos continúan en rangos controlables por los métodos de refuerzo establecidos. Debido a los beneficios económicos de esta disposición y con el fin de garantizar la estabilidad, puede ser rentable mejorar selectivamente el refuerzo con cableado.
En este estudio no se consideraron aspectos hidrogeológicos que pudieron modificar las condiciones de estabilidad del terreno. Así mismo, y fundamentalmente debido a las consideraciones de flujo plástico, esta simulación obtuvo resultados conservadores.
Finalmente, sobre la aplicación del método de elementos finitos en macizos rocosos, debe resaltarse que estos materiales son por lo general discontinuos, anisotrópicos, no homogéneos y no elásticos, por ello deben considerarse las características y limitaciones de este método; para profundizar en estas consideraciones recomendamos trabajos como el de Jing (2003). Para mejorar los modelos de excavaciones en medios rocosos es necesario aumentar el número de muestras ensayadas en laboratorio, en lo posible con pruebas esfuerzo-deformación en etapa post-falla, modelar en dominios de menor tamaño e incluir el tensor de esfuerzos medido in situ.
En un modelo más elaborado sería necesario incluir aspectos del fracturamiento del terreno rocoso debido a sus efectos de disminución del grado de estabilidad, para lo cual se puede acudir a métodos como el de Elementos Discretos (DEM) o el de Red de Fracturas Discretas (DFN). Así mismo es posible integrar los modelos numéricos con el monitoreo del comportamiento del macizo rocoso y de las excavaciones bajo la variación de condiciones de calidad geomecánica y del estado de esfuerzos.
FINANCIACIÓN Y AGRADECIMIENTOS
Este estudio fue financiado por la Dirección de Investigaciones de la Universidad Nacional de Colombia, Sede Medellín en el proyecto: “Modelación reológica de rocas con fines de diseño de excavaciones”, y Argos. Agradecemos la participación del profesor Oswaldo Bustamante y los auxiliares de investigación Alvaro Andrés Perez, Diliany Ramirez Ospina y Victor Florez Mejía.
REFERENCIAS
[1] Ansys Tutorials V. 9.0. 2005. Ansys Inc. Southpointe 275 Technology Drive. Canonsburg, PA 15317, USA.
[2] Carranza -Torres, C. y Fairhurst, C. 1999.The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek-Brown failure criterion. International Journal of Rock Mechanics and Mining Sciences, Vol. 36, Pergamon.
[3] Cardona A. 2006. La relación esfuerzos inducidos-permeabilidad en excavaciones subterráneas de gran diámetro. Tesis de Maestría. Universidad Nacional de Colombia.
[4] Hoek E. y Brown E. T. 1997. Practical estimates of rock mass strength. Int. Journal of rock mechanics and Min. Sciences. Vol 34, No. 8, pp. 1165-1186.
[5] Hoek E. 2001. Rock mass properties for underground mines en Underground mining methods: Engineering fundamentals and international case studies, Society for Mining, Metallurgy and Exploration, Litleton Colorado, 2001.
[6] ICP-ECOPETROL. 2005. Informe de resultados de pruebas mecánicas para Cementos El Cairo.
[7] Gil E. F. 1996. Aspectos geológicos de los cuerpos calcáreos de la región de la Merced- Montebello. Tésis de pregrado. Universidad Nacional de Colombia, Medellín.
[8] Jing, L. A. 2003. Review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int. Journal of rock mechanics and Mining Sciences. Vol 40, pp.283-352.
[9] Jing L. y Hudson J. A. 2002. Numerical methods in rock mechanics. Int. Journal of rock mechanics and Mining Sciences. Vol 39, pp. 409-427.
[10] Moaveni S. 1999. Finite element análisis, theory and application with Ansys. Prentice Hall.
[11] Martin C. D. et al. 2003. Stress, instability and design of underground excavations. Int.
[12] Journal of rock mechanics and Mining Sciences. Vol 40, pp.1027-1047.
[13] Ofoegbu G. I., Curran J. H. 1992. Deformability of intact rock. Int. Journal of rock mechanics and Min. Sciences. Vol 29, pp. 35-48.
[14] Nasseri M. H. B. et al. 2003. Anisotropic strength and deformational behavior of Himalayan schist. Int. Journal of rock mechanics and Min. Sciences. Vol 40, pp. 3-23.
[15] RocLab. Version 1.021 2006. Hoek-Brown Criterion.
[16] Tobon J. I. y Monsalve J. E. 2001. El sublevel stoping aplicado a la mina de caliza El Toro, de Cementos El Cairo. Universidad Nacional de Colombia, Boletín de Ciencias de la Tierra 14. pp. 59-78.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2007 Boletín de Ciencias de la Tierra

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista. Al asumir los derechos patrimoniales del artículo, no podrá reproducirse parcial o totalmente en ningún medio impreso o digital sin permiso expreso del mismo.




















