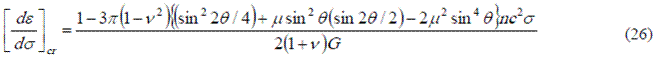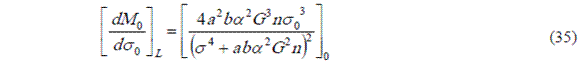LA FALLA DE LA ROCA
LA FALLA DE LA ROCA
THE FAILURE OF ROCK
COOK,N.G.W.
Transvaal and Orange
Free State Chamber of Mines, Johanneshburg, South Africa
Estudiante de
Doctorado en Geotecnia de ¡a Universidad de Brasilia-Brasil
lsuarezburgoa@unb.br
Recibido para evaluación: 29 de Septiembre de 2009 / Aceptación: 15 de Octubre de 2009 Recibida versión final: 20 de Noviembre de 2009
El artículo original
en idioma inglés fue publicado en International Journal of Rock Mechanics and
Mining Sciences, Vol. 2. Cook, N.GW., The failure of rock. pp. 389-403, derechos
de copia Elsevier (1965).El documento original fue escrito en unidades de
centímetros, dinas y ergios, las cuales fueron convertidas a unidades del
sistema internacional: metro, newton y julios 
RESUMEN
Aparentemente no se
tiene información disponible concerniente al comportamiento inelástico de las
rocas fuertes, cuando el sistema comúnmente usado para determinar la
resistencia de muestras de roca, llega a ser inestable inmediatamente después
que se alcanza el pico de la relación deformación-esfuerzo, y cuando su
pendiente alcanza a ser negativa. Se hace un análisis de los cambios de energía
asociados con la extensión de fisuras tipo Griffith a tracción
y compresión, que muestran que el comportamiento inelástico puede ser descrito
por el lugar geométrico curvo tipo Griffith. en el plano deformación-esfuerzos.
Solamente cuando la pendiente (de ds) de este espacio geométrico es mayor a
cero, el material es intrínsecamente frágil y pasible a una fractura
espontánea. Cuando de ds es menor a cero, es posible que continúe la extensión
de la fisura por fracturación inestable ó falla estable, dependiendo de la
cantidad de energía suministrada al material por el sistema de aplicación de
carga. El efecto del confinamiento triaxial reduce la pendiente negativa del
lugar geométrico tipo Griffith y hace que el material sea más dúctil que cuando
éste está bajo mía compresión uniaxial. La actividad micro-sísmica durante el
ensayo de muestras de roca puede explicarse asumiendo que la roca es un
material heterogéneo con inclusiones elásticas, y analizando la fractura de
estas inclusiones en términos a lo expresado arriba. Se presentan datos
experimentales obtenidos de ensayos de compresión uniaxial del mármol de
Tennessee y el granito de Saint-Cloud y se muestran que están de acuerdo con
las predicciones analíticas.
PALABRAS CLAVES: (el documento original no tiene palabras clave) Mecánica de rocas. Falla frágil.
ABSTRACT
Vírtually no infomation
concerning the non-elastic behavior of hard rock is available. as the systems
usually used to determine the strength of rock specimens become unstable as
soon as the peak of the strain-stress characteristics is passed and its slope
becomes negative. An analysis of the energy changes associated with the
extensión of Griffith cracks in tensión and compression is made. which shows
that the non-elastic behavior can be described by a curved
Griffith locus in the strain-stress plane. Only when the slope of this locus de
ds>0, is a material intrinsically brittle and liable to spontaneous
fracture. When dé ds<0. crack extensión can proceed by unstable fracture or
stable failure. depending upon the amount of energy supplied to the material by
the loading system. The effect of triaxial confinement is to reduce the
negative slope of the Griffith locus and make the material more ductile than it
is in uniaxial compression.
Micro-seismic activity during the testing of rock specimen can be accounted for
by assuming that rock is a heterogeneous material containing elastic
inclusions. and analyzing the fracture of these inclusions in terms of the
above. Experimental data obtained from uniaxial compression tests on Tennessee
marble and Saint Cloud granite is presented and is shown to be in accord with
the analytical predictions.
KEYWORDS: (Original document has no keywords) Rock mechanics. Brittle failure.
1. INTRODUCCIÓN DEL TRADUCCTOR
Podría ser poco atractivo, en primera instancia, haber elegido un documento antiguo como éste, para ser traducido al idioma español, teniendo en cuenta que en la actualidad existe mía cierta cantidad de literatura en este idioma, más no amplia, sobre el concepto fundamental de la «falla de la roca». No obstante el presente artículo, escrito por el Profesor' Neville Cook en 1965. fue uno de los más importantes de la época que dio las bases de los actuales modelos de la mecánica de las fracturas aplicados a rocas, empleado para entender el comportamiento frágil de la roca y el fenómeno de estallido de la misma, frecuentemente encontrados en las minas subterráneas.
El Profesor John A. Hudson (2001) [En: Editorial. Int. J. Rock Mech. & Min. Ser.. Vol. 37(1-2). pp. 3-5] comenta sobre el presente artículo si yo muera que escoger el artículo que más me influyó en la mecánica de las rocas..."- refiriéndose a todas las contribuciones que hizo el profesor Cook. -»... escogerla -La Falla de la Roca-.... que' tirulo tan sucinto y que deducciones».
Este artículo fue el primero en analizar la influencia de las fisuras relacionando el módulo de Young efectivo, así como la resistencia de la roca. Permitió el uso del concepto de lugar geométrico de Griffith para describir el ablandamiento por deformaciones de las rocas.
Hasta ahora, ningún libro en idioma español ha tocado el tema con tanta claridad y detalle como lo explicó en aquella oportunidad, en idioma inglés, el autor del presente artículo. Este documento científico es considerado clásico dentro de la mecánica de rocas y servirá como base fundamental para tener una explicación con sólidas referencias acerca del proceso que se menciona. En el Apéndice B de esta traducción resumí mía breve biografía del Profesor Neville Cook.
2. INTRODUCCIÓN
Originalmente Griffith (1921) definió la baja resistencia a tracción de los materiales frágiles en términos de una desigualdad entre la tasa en que la energía elástica se disipa y la tasa en la cual la energía de superficie es absorbida, cuando un defecto o fisura se extiende en el material. Ampliaciones subsecuentes de la teoría de Griffith a condiciones de esfuerzo de compresión, incluyendo esfuerzos triaxiales, han definido usualmente la resistencia de los materiales frágiles en términos de un esfuerzo critico a tracción, concentrado cerca del canto del defecto o fisura (Orowan. 1949). Usando este criterio. McClintocky Walsh (1962) calcularon el plegamiento de fisuras tipo Griffith bajo compresión, y sus resultados fueron mostrados por Brace (1960) y Hoek (Cook. 1963) para proveer una adecuada descripción de la resistencia de las rocas fuertes.
La resistencia de la
roca usualmente se determina usando mía prensa para aplicar una carga axial
incremental a una muestra libre o confinada, donde se registra el esfuerzo al
cual el sistema prensa-muestra alcanza la inestabilidad. El sistema llega a
ser" inestable a alguna pendiente negativa de la curva
deformación-esfuerzo, determinada por la resiliencia de la prensa. Debido a la
relativa alta resiliencia de muchas prensas, la inestabilidad usualmente ocurre
a bajas pendientes negativas muy cercanas al pico de la curva deformación-esfuerzo
de la roca. En el caso de rocas fuertes, el pico por lo general coincide con la
transición del comportamiento elástico a inelástico. Así. aparentemente no se tiene
disponible ninguna información relacionada con el comportamiento inelástico de
la roca fuerte. Así como es importante conocer la resistencia de la roca, es
igualmente importante en estudios de problemas de dinámica tales
como el estallido de rocas (i.e. rockburting) y procesos de perforación,
conocer cuánta energía se absorbe en el proceso de rotura. El trabajo mostrado
en este artículo considera los cambios de energía asociados con la extensión de
las fisuras tipo Griffith. y por consiguiente define el comportamiento inelástico
de las rocas fuertes. Para fisuras simples sometidas a esfuerzos de tracción,
los resultados son coincidentes con el lugar geométrico de Griffith obtenido por
Berry (1960). al considerar la emética de la tracción y el clivaje de la
fractura. Un similar lugar geométrico se obtuvo para fisuras cerradas sometidas
a esfuerzos de compresión, donde se encontró el correspondiente criterio de
resistencia coincidente con el criterio de Mohr-Coulomb.
3. TEORÍA
3.1. Tracción
Como introducción a este análisis, considere primero el caso clásico de una sola fisura de longitud 2c. en la forma de una elipse aplanada (i.e. elipse con excentricidad cercana a uno), bajo un estado plano de deformaciones normal al esfuerzo de tracción, s. aplicado externamente a mía muestra de longitud /. ancho b. y espesor unitario (Figura 1).
Imagine que inicialmente el esfuerzo se mantiene constante, manteniendo cerradas las superficies de la fisura a través de algún mecanismo. Si a continuación las superficies de estas fisuras son relajadas lentamente, se hará un trabajo Ws en el mecanismo de plegamiento y se almacenará una energía de deformación adicional Ws al rededor de la fisura (Ecuación. 1). donde G es el módulo de rigidez y n es la relación de Poisson (Orowan. 1949).
La energía de deformación (S..E) en la ausencia de la fisura será igual a la expresión de la Ecuación 2

Figura 1. Lugar
geométrico de Griffith de una fisura perpendicular a la carga uniaxial
Define el confortamiento inelástico a
tracción de un material para n=10. donde la energía superficial  ergios.
ergios.  y el módulo de
rigidez
y el módulo de
rigidez  dinas em2 (50 GPa).
dinas em2 (50 GPa).
Si -s es la deformación asociada con el
esfuerzo aplicado externamente ( a) en la presencia de la fisura, entonces el
trabajo total (WD.) hecho por la aplicación de -o es igual a lo
siguiente (Ecuación. 3).
Ahora,

De donde.
Siendo n el número de fisuras por unidad de volumen de roca, donde el producto b¡ es igual al volumen por cada mudad de fisura.
Estas ecuaciones son
obviamente exactas para una sola fisura en un plano infinito, siendo la
evaluación del efecto de varias fisuras finitas por unidad de volumen (i.e.
densidad de fisuras) mi problema altamente complejo. La estimación de la
magnitud de la influencia de la fisura, y por consiguiente la validez del
análisis simplificado, puede ser obtenida con la solución de Salomón (1964).
para una clase infinita de fisuras de forma alargada y de poco espesor,
paralelas,
coplanares y normales al esfuerzo principal. El calculó la razón del volumen de
la serie de fisuras con aquel volumen de una sola, aislada y similar fisura. El
volumen de la candad de la fisura logró mostrar ser proporcional a la energía
de deformación debido a la presencia de la misma. Estos resultados muestran que
cuando las fisuras ocupan 50% de la sección transversal, la energía adicional
de deformación debido a su interacción es de 12,4%, y cuando la fisura ocupa
el 90% de la sección transversal, la energía adicional de deformación es de
S5.7%. En este análisis, son significantes tanto la energía total de
deformación como su tasa de cambio con el incremento del tamaño de la fisura.
La solución de Salomón (1964) muestra que estas dos cantidades aumentan con el
incremento de la densidad de las fisuras, pero que ésta última (i.e. la tasa de
cambio con el incremento del tamaño de la fisura) incrementa más rápidamente
que la primera (i.e. la energía adicional de deformación). De este modo, el
análisis simplificado proveerá una buena solución cuantitativa para bajas
cantidades de fisuras por mudad de volumen, y mía solución cualitativa para
altas cantidades de fisuras por unidad de volumen.
El criterio, para propagar o fallar una fisura, es que la derivada del trabajo We respecto a la semi longitud de la fisura, c sea mayor a cuatro veces la energía superficial de la fisura, a. (Ecuación 6).
Esto quiere decir que se cumpla la desigualdad de la Ecuación 7.
Substituyendo el valor crítico de c de la Ecuación 7 dentro de la Ecuación 5 se tiene la siguiente expresión de la deformación crítica (Ecuación8). que tiene mía pendiente según la Ecuación 9.

La Ecuación 5 define las trayectorias de deformación-esfuerzo para diferentes tamaños de fisuras y densidades de éstas antes de la falla; y la Ecuación 3. que es el plano de deformación equivalente al lugar geométrico de Griffith definido por Berry (1960), define aquella región en el plano deformación-esfuerzo dentro del cual es válida la Ecuación 5.
El lugar geométrico de Griffith. por consiguiente define la trayectoria deformación-esfuerzo, donde el material falla debido a la tracción concurrente de un determinado número de fisuras idénticas. La Fisura 1 muestra las Ecuaciones 5 y 8 en el plano deformación-esfuerzo (plano e-o) para diferentes tamaños de fisuras, representadas por la semi-longitud de su eje mayor (c), con valores típicos asignados a las variables a, Gy n. Cuando inicia la falla, la trayectoria que recorre en el plano s-o depende de las características externas de los esfuerzos aplicados. Por ejemplo, si a se aplica de tal forma de que sea constante, independientemente del desplazamiento, la trayectoria después de la falla será paralela al eje de las deformaciones (eje s). y si el borde donde ase aplica se mantiene fijo en el momento de la falla, la trayectoria será paralela al eje de los esfuerzos (eje a). Prácticamente, muchos de los esfuerzos aplicados tienen características que se mantienen entre estos dos extremos.
La energía absorbida por la falla, o la extensión de la fisura, es proporcional al área delimitada por la Ecuación S y la Ecuación 5. con la apropiada longitud inicial y final de la fisura. Por consiguiente, la energía liberada durante la falla es proporcional a la diferencia entre esta área y la energía de entrada por mudad de volumen, esto quiere decir, el área entre el eje e y la trayectoria de los esfuerzo aplicados externamente.
Una fractura inestable puede definirse como mía falla acompañada por la liberación de la energía. Las trayectorias de los esfuerzos externos que conducen la falla y propagación de fisuras (i.e. fracturación), se muestran con las flechas 1 y 2 en la Figura 1. respectivamente. En el caso de mi esfuerzo externo aplicado con los bordes fijos, la fracturación solo puede ocurrir si <k/dj es mayor a cero. De este modo, solo los materiales en donde se cumpla la desigualdad de la Ecuación 10 son intrínsecamente frágiles y susceptibles a mía fracturación espontánea sin la adición externa de energía durante su proceso. De otro modo, es posible seguir la trayectoria definida por la Ecuación S en mía manera casi estática, durante la cual la falla ocurrirá a través de la extensión estable de las fisuras hasta que la longitud de cada una sea igual al ancho b.
3.2. Compresión
En el segundo caso considere una fisura de longitud 2 c en la forma de una elipse aplanada en un estado plano de deformaciones e inclinada a un dado ángulo 9 hacia la dirección del esfuerzo compresivo uniaxial aplicado sobre la muestra de longitud /. ancho b y espesor unitario (Figura 2).
La fisura entonces está sujeta a esfuerzos
compresivos  dados por las
Ecuaciones 11 y 12, paralelo y normal a su longitud, respectivamente; y a un
esfuerzo cortante t paralelo a su superficie, dado por la Ecuación 13.
dados por las
Ecuaciones 11 y 12, paralelo y normal a su longitud, respectivamente; y a un
esfuerzo cortante t paralelo a su superficie, dado por la Ecuación 13.
Debido a que la
fisura se cierra, surgirá una fuerza de fricción  a lo largo de la superficie de la fisura, donde |.i es el coeficiente de
fricción de estas superficies.
a lo largo de la superficie de la fisura, donde |.i es el coeficiente de
fricción de estas superficies.
Imagine que los
esfuerzos se mantienen constantes, inicialmente con las superficies de las
fisuras mantenidas cerradas por algún mecanismo. Si luego, las superficies de
las fisuras se liberan lentamente, ellas se deslizarán una con otra debido a
que  En este proceso, el trabajo
En este proceso, el trabajo  se hará dentro del mecanismo cerrado y
el trabajo
se hará dentro del mecanismo cerrado y
el trabajo  se hará en contra de
las fuerzas de fricción, mientras que una energía de deformación adicional
se hará en contra de
las fuerzas de fricción, mientras que una energía de deformación adicional  se almacenará alrededor de la fisura
cuando m llegue a ser igual a cero (Ecuación l4) (Starr. 1928).
se almacenará alrededor de la fisura
cuando m llegue a ser igual a cero (Ecuación l4) (Starr. 1928).
De este modo, cuando  es mayor a cero (Ecuación 15) (Ver
Apéndice A) la energía de deformación en la ausencia de la fisura será igual a
la expresión de la Ecuación 16.
es mayor a cero (Ecuación 15) (Ver
Apéndice A) la energía de deformación en la ausencia de la fisura será igual a
la expresión de la Ecuación 16.
Si s es la deformación asociada a la aplicación de o en la presencia de la fisura, el trabajo total hecho por la aplicación del esfuerzo o está dado según la Ecuación 17.
Entonces se tiene la siguiente igualdad (Ecuación 18) (Ver Apéndice A), de donde se obtiene la expresión de la deformación asociada a la aplicación de s en la presencia de la fisura (Ecuaciónl9).
El criterio de la extensión de la fisura o proceso de falla es también igual a la expresión de la Ecuación 6. de este modo se obtiene las expresiones Ecuación 20 y Ecuación 21 (Ver Apéndice A).
Por consiguiente, la condición crítica para la iniciación de la falla debe hacer cumplir la expresión de la Ecuación 22, que puede ser escrita como la expresión Ecuación 23 o Ecuación 24.
Por consiguiente, la condición crítica para la iniciación de la falla debe hacer cumplir la expresión de la Ecuación 22, que puede ser escrita como la expresión Ecuación 23 o Ecuación 24.
La última expresión (Ecuación 24) es la misma
para el estado de compresión triaxial y coincide con la envolvente de Mohr-Coulomb
en el plano del esfuerzo normal y esfuerzo de corte 
Sustituyendo el valor crítico de c de la Ecuación 23 en la Ecuación 19 se obtiene la expresión de e (Ecuación25) que tiene mía pendiente según la expresión de la Ecuación 26.
La Ecuación 19 define
las trayectorias lineales deformación-esfuerzo antes de la falla, y la Ecuación
25, lugar geométrico de Griffith. define aquella región del plano  donde la Ecuación 19 es válida. Estas
ecuaciones se muestran en la Figura 2 para valores típicos de
donde la Ecuación 19 es válida. Estas
ecuaciones se muestran en la Figura 2 para valores típicos de  escogido de tal forma que la expresión
escogido de tal forma que la expresión  dé el valor máximo. La Ecuación
23 muestra que la extensión de la fisura comienza cuando alcanza un valor
crítico. Se puede mostrar que esta expresión (Ecuación23). que es función de 9,
tiene mi máximo bien definido cerca de algún valor óptimo de ө. cuando el
coeficiente de fricción es cercano a la unidad. Esto justifica el supuesto de
que todas las fisuras activas son inclinadas en o cerca del valor óptimo de 0.
La Figura 2 muestra que el lugar geométrico de Griffith a compresión uniaxial
es similar al mismo en tracción (Figura 1). y las mismas consideraciones se
aplican cuando se comenta de la falla y la energía liberada en la fractura.
dé el valor máximo. La Ecuación
23 muestra que la extensión de la fisura comienza cuando alcanza un valor
crítico. Se puede mostrar que esta expresión (Ecuación23). que es función de 9,
tiene mi máximo bien definido cerca de algún valor óptimo de ө. cuando el
coeficiente de fricción es cercano a la unidad. Esto justifica el supuesto de
que todas las fisuras activas son inclinadas en o cerca del valor óptimo de 0.
La Figura 2 muestra que el lugar geométrico de Griffith a compresión uniaxial
es similar al mismo en tracción (Figura 1). y las mismas consideraciones se
aplican cuando se comenta de la falla y la energía liberada en la fractura.
La condición bajo
esfuerzos triaxiales puede analizarse de la misma manera, asumiendo que la
fisura es paralela a la dirección del esfuerzo compresivo intermedio usando las
relaciones expresadas en las Ecuaciones 27 y 28, donde  y
y  son el esfuerzo compresivo
máximo y mínimo, respectivamente.
son el esfuerzo compresivo
máximo y mínimo, respectivamente.
El lugar geométrico
de Griffith para la compresión triaxial se ilustra también en la Figura 2 para
los mismos valores de  . Esta
muestra que la pendiente negativa del lugar geométrico de Griffith. para
cualquier tamaño dado, es reducida por el esfuerzo de confinamiento. Como
resultado de esto, la roca resulta ser menos susceptible a una fracturación
inestable y parece ser más dúctil; que está de acuerdo con la observación
experimental de Von Karman (1911).
. Esta
muestra que la pendiente negativa del lugar geométrico de Griffith. para
cualquier tamaño dado, es reducida por el esfuerzo de confinamiento. Como
resultado de esto, la roca resulta ser menos susceptible a una fracturación
inestable y parece ser más dúctil; que está de acuerdo con la observación
experimental de Von Karman (1911).
3.3. Micro-sismicidad
Muchas rocas se componen de agregados heterogéneos localizados en diferentes partes, que pueden diferir en su comportamiento mecánico. Asuma que las mayores partes heterogéneas puedan considerarse como inclusiones elásticas en un entorno aproximadamente homogéneo y elástico. Cuando aquella roca es sometida a esfuerzos de compresión, el esfuerzo en cada inclusión será diferente de aquel del entorno, y la inclusión podrá fallar en una forma estable o inestable antes de que la roca falle, como un todo: dependiendo de las propiedades mecánicas relativas de la inclusión y del entorno. La fractura inestable de estas inclusiones puede aumentar la actividad micro-sísmica que es generalmente observada en muestras de roca sometidas a esfuerzos de compresión. En esta parte, estas consideraciones son analizadas para el caso de la roca bajo esfuerzo compresivo uniaxial.
Muskelishvili (1953)
analizó los efectos de las inclusiones elásticas circulares en un entorno
elástico. El demostró que para un estado de compresión uniaxial de deformación
plana, la relación entre el esfuerzo en la inclusión  y aquel esfuerzo en el entorno
y aquel esfuerzo en el entorno  está en función del módulo efectivo de Young (afectado por las fisuras) M el módulo efectivo de Young de las inclusiones
está en función del módulo efectivo de Young (afectado por las fisuras) M el módulo efectivo de Young de las inclusiones  .
para mía relación de Poisson igual a v= 0,25, tanto para el material de la inclusión
como para del entorno (Ecuación 29).
.
para mía relación de Poisson igual a v= 0,25, tanto para el material de la inclusión
como para del entorno (Ecuación 29).
Físicamente, la condición para que la inclusión falle primero es que oo debe exceder la resistencia de la inclusión antes que o exceda la resistencia del material del entorno. Una vez que esta condición se satisfaga, la falla de la inclusión puede ser estable o mestable. dependiendo de que si la trayectoria de esfuerzos aplicado a la inclusión esté dentro (flecha 1) o fuera (flecha 2) del lugar geométrico de Griffith referente a la inclusión, como se muestra en la Figura 1.
La Ecuación 25 del lugar geométrico de Griffith puede ser reescrita según la Ecuación 30. donde a y b se expresan según las Ecuaciones 31 y 32; y el lugar geométrico puede expresarse en términos del módulo efectivo de Young My el esfuerzo en el entorno cuando se inicia la falla, g (Ecuación 33).
Considerando el lugar
geométrico de Griffith en el plano  como se ilustra en la Figura 3c, y recordando que My g sólo pueden
disminuir durante la fractura, es posible observar que el criterio de fractura
inestable de la inclusión puede expresarse según la siguiente expresión
(Ecuación34), donde el subíndice L se refiere al lugar geométrico de Griffith
correspondiente a la inclusión y el subíndice Sse refiere al
esfuerzo aplicado a la inclusión a través del entorno.
como se ilustra en la Figura 3c, y recordando que My g sólo pueden
disminuir durante la fractura, es posible observar que el criterio de fractura
inestable de la inclusión puede expresarse según la siguiente expresión
(Ecuación34), donde el subíndice L se refiere al lugar geométrico de Griffith
correspondiente a la inclusión y el subíndice Sse refiere al
esfuerzo aplicado a la inclusión a través del entorno.
De la Ecuación 33 se obtiene la Ecuación 35 y de la Ecuación 29 se obtiene la Ecuación 36. por consiguiente la fractura inestable de la inclusión puede ocurrir si se cumple la desigualdad de la Ecuación 37, sabiendo que para el caso de la inclusión se cumple la igualdad de la Ecuación 38 y para el caso del entorno se cumple la desigualdad de la Ecuación 39.
Si la desigualdad de
la Ecuación 37 no se satisface, pero se cumplen la igualdad de la Ecuación 33 y
la desigualdad de la Ecuación 39. la falla de la inclusión será estable. Las
expresiones izquierda y derecha de la desigualdad de la Ecuación 37 se grafican
en la Figura 3a respecto el esfuerzo de la inclusión.  donde la falla comienza, para el caso de dos densidades de fisuras como inclusiones
y un módulo de Young del entorno, usando valores típicos de
donde la falla comienza, para el caso de dos densidades de fisuras como inclusiones
y un módulo de Young del entorno, usando valores típicos de  y
y  .
Estos valores se asumen ser los mismos tanto para el material del entorno como
para el material de las inclusiones, de este modo solo vana la densidad de las
fisuras. La Figura 3a se refiere solo al inicio de la falla de la inclusión,
donde las Ecuaciones 29 y 33 se usaron para eliminar M y o del lado derecho de
la desigualdad (Ecuación37). Tan pronto inicia la fractura inestable de la
inclusión, el esfuerzo presente en la inclusión y el esfuerzo que define su
lugar geométrico no será más el mismo, y la igualdad entre
.
Estos valores se asumen ser los mismos tanto para el material del entorno como
para el material de las inclusiones, de este modo solo vana la densidad de las
fisuras. La Figura 3a se refiere solo al inicio de la falla de la inclusión,
donde las Ecuaciones 29 y 33 se usaron para eliminar M y o del lado derecho de
la desigualdad (Ecuación37). Tan pronto inicia la fractura inestable de la
inclusión, el esfuerzo presente en la inclusión y el esfuerzo que define su
lugar geométrico no será más el mismo, y la igualdad entre  y las Ecuaciones 29 y 33 dejan de
tener efecto. El esfuerzo en el entorno,
y las Ecuaciones 29 y 33 dejan de
tener efecto. El esfuerzo en el entorno,  correspondiente al esfuerzo en las inclusiones.
correspondiente al esfuerzo en las inclusiones.  .
donde se inicia la falla: se muestra en la Figura 3b haciendo uso de las
Ecuaciones 29 y 33. Los lugares geométricos de Griffith para entornos con
diferentes densidades de fisuras se muestran en la Figura 3c.
.
donde se inicia la falla: se muestra en la Figura 3b haciendo uso de las
Ecuaciones 29 y 33. Los lugares geométricos de Griffith para entornos con
diferentes densidades de fisuras se muestran en la Figura 3c.
Esta figura puede
usarse juntamente con la Figura 3b para determinar si los requisitos de
esfuerzo, Ecuaciones 38 y 39. se satisfacen. Esto quiere decir si  del entorno están por encima de la parte
achurada. Usando la Figura 3 para considerar cualquier caso que permita con
antecedencia mía fractura inestable de la inclusión, se puede observar que cuando
el esfuerzo del contorno incrementa, la desigualdad de la Ecuación 37 llega a
ser más importante y que se fracturarán las sucesivas inclusiones más fuertes.
Al mismo tiempo, el esfuerzo en el entorno se acerca al lugar geométrico de
Griffith donde el material del entorno fallaría. Por tanto, la actividad
micro-sísmica en la roca que contenga muchas inclusiones heterogéneas, tenderá
a incrementar a medida que el esfuerzo en la roca se incremente hasta la falla
última de la roca que ocurre como un todo.
del entorno están por encima de la parte
achurada. Usando la Figura 3 para considerar cualquier caso que permita con
antecedencia mía fractura inestable de la inclusión, se puede observar que cuando
el esfuerzo del contorno incrementa, la desigualdad de la Ecuación 37 llega a
ser más importante y que se fracturarán las sucesivas inclusiones más fuertes.
Al mismo tiempo, el esfuerzo en el entorno se acerca al lugar geométrico de
Griffith donde el material del entorno fallaría. Por tanto, la actividad
micro-sísmica en la roca que contenga muchas inclusiones heterogéneas, tenderá
a incrementar a medida que el esfuerzo en la roca se incremente hasta la falla
última de la roca que ocurre como un todo.
4. EXPERIMENTO
4.1. Descripción
El lugar geométrico Griffith para describir el comportamiento inelástico de mía roca fuerte Se desarrolló basado en asumir que un número dado de fisuras, todas del mismo tamaño, se extienden simultáneamente. Los defectos en las rocas ciertamente siempre consisten de fisuras de diferentes tamaños, que pueden comenzar a extenderse a diferentes estados de esfuerzos. En un material completamente homogéneo la primera fisura en extenderse crecerá a una mayor fractura. La naturaleza heterogénea de la roca actúa casi como si aquella fisura se extendiera solo mía pequeña distancia antes que sea frenada por una región de mayor resistencia a la propagación de fisuras.
La fisura empezará a extenderse nuevamente solo bajo algún esfuerzo superior, después que otras fisuras ya hayan empezado a extenderse. De este modo, es razonable suponer que el comportamiento inelástico de un material heterogéneo, como la roca, pueda definirse como la representación del lugar geométrico Griffith. de acuerdo a la distribución de las fisuras de diferentes tamaños presentes en la roca. El efecto de tal representación hará que se altere la transición entre el comportamiento del estado elástico e inelástico de mi cambio discontinuo a uno continuo.
Cuando surge el lugar geométrico de Griffith de la extensión de fisuras, la pendiente de la transición modelada puede esperarse que dependa de la extensión de la fisura.
Una serie de ensayos de compresión uniaxial fueron conducidos en prismas rectangulares del mármol de lemiessee. mía roca fuerte relativamente homogénea; y en el granito de Sainr-C¡oud mía roca fuerte relativamente heterogénea. Estas muestras fueron trabajadas en una pulidora de superficie hasta alcanzar las dimensiones nominales de 3,75x 3.75x 15 cm o 3,75x 5.00x 15 cm siendo cuidadosos de asegurar que sus extremos sean paralelos con una exactitud de 0.001 cm. Estas fueron cargadas en forma paralela a su eje longitudinal, usando un mecanismo que se ilustra en la Figura 4. a través de una máquina hidráulica para ensayos de compresión.
Se hizo el intento de reducir los llamados efectos terminales a mi mínimo. a través de una placa de acero fuerte con la misma sección transversal que los prismas, a cada extremo de la muestra; lubricando con di-sulfato de molibdeno la interface entre esta placa y la placa de carga de acero fuerte.
El objetivo de estos ensayos fue de estudiar las relaciones entre lo siguiente:
• La resiliencia del sistema de carga y la violencia del proceso de fracturación.
• La pendiente de la curva deformación-esfuerzo y la extensión de las fisuras presentes en la roca.
• La actividad micro-sísmica, la curva deformación-esfuerzo y la heterogeneidad de la roca.

Figura 4. Aparato
de ensayo. Para determinar las características deformación-esfuerzo de muestras
de roca y para incrementar la rigidez de la máquina de ensayos a compresión.
La resiliencia
ordinaria de la máquina de ensayo fue de  dinas/cm (270 MN/m), y ésta fue incrementada a
dinas/cm (270 MN/m), y ésta fue incrementada a  dinas cm(l 350 MN/m) a través de cargar en paralelo con la muestra de roca un
tubo de acero (Figura 4).
dinas cm(l 350 MN/m) a través de cargar en paralelo con la muestra de roca un
tubo de acero (Figura 4).
La carga en la muestra de la roca y su acortamiento axial fueron registrados como curvas deformación-esfuerzo en una registradora de coordenadas de ejes cartesianos abscisas-ordenadas (registradora de coordenadas x-y). Para registrar la envolvente de la actividad micro-sísmica, se usó un cristal piezo-eléctrico adherido a la muestra, que alimenta un amplificador y un rectificador de señales; a través de otra registradora de coordenadas x-y. donde se usó la variable de deformación como lectura en el eje de las abscisas.
4.1. Resultados
La teoría sugiere que se necesita energía, en adición a aquella almacenada como energía de deformación en la muestra de roca, para producir falla de la muestra. Asumiendo que la carga se aplica en forma cercana a ser estática, la energía adicional puede ser provista solo de la energía almacenada por la resiliencia de la máquina de ensayo. Como correspondería, es posible reducir la violencia de la fractura, incrementando la rigidez de la máquina de ensayo, y en el caso extremo, prever la fractura violenta de todo el conjunto. La Figura 5 muestra las curvas deformación-esfuerzo obtenidas de cargar hasta la fractura dos muestras similares del mármol de Tennessee. para el caso de una máquina flexible (curva 1) y una rígida (curva 2).

Figura 5. Curva
deformación-esfuerzo del mármol de Tennessee Obtenido en una máquina flexible y
una rígida durante ensayos de compresión hasta la falla.
La resiliencia de la
máquina se muestra en esta figura (Figura 5) por las líneas con pendientes
negativas. -k correspondiente a las resiliencias de  dinas cm (270 MN/m) y -a08ecu43.gif-
dinas cm (270 MN/m) y -a08ecu43.gif-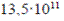 dinas/cm (1 350 MN ni), para las curvas
1 y 2 respectivamente. Se puede observar que la rotura de la muestra ocurre muy
rápido, cuando la pendiente de la curva deformación-esfuerzo
dinas/cm (1 350 MN ni), para las curvas
1 y 2 respectivamente. Se puede observar que la rotura de la muestra ocurre muy
rápido, cuando la pendiente de la curva deformación-esfuerzo  es mayor a mío. La rotura que ocurrió
durante el ensayo con la configuración de la máquina flexible fue tan violenta,
que el golpe de la máquina logró ser percibido en toda la extensión del
edificio del laboratorio. La rotura que ocurrió durante el ensayo con la
configuración de máquina rígida no fue muy Violenta y difícilmente produjo un golpe perceptible.
Esto sugiere que casi toda la energía almacenada por la resiliencia de la máquina
rígida fue absorbida por la deformación inelástica de la muestra, por lo que el
lugar geométrico de Griffith debió estar cerca de las características de la
máquina.
es mayor a mío. La rotura que ocurrió
durante el ensayo con la configuración de la máquina flexible fue tan violenta,
que el golpe de la máquina logró ser percibido en toda la extensión del
edificio del laboratorio. La rotura que ocurrió durante el ensayo con la
configuración de máquina rígida no fue muy Violenta y difícilmente produjo un golpe perceptible.
Esto sugiere que casi toda la energía almacenada por la resiliencia de la máquina
rígida fue absorbida por la deformación inelástica de la muestra, por lo que el
lugar geométrico de Griffith debió estar cerca de las características de la
máquina.
Desafortunadamente no fue posible incrementar la rigidez de la máquina más allá de mi valor significante. Por consiguiente, el lugar geométrico Griffith completo, no puede ser obtenido teóricamente con una máquina de rigidez infinita.
Si la pendiente de la
curva deformación-esfuerzo se debe a la extensión de la fisura, esto debería detectarse
con el cambio en la resistencia a tracción de la roca, que es teoréticamente
sensible al tamaño de la fisura. De acuerdo a esto, se sometieron mía serie de
muestras semejantes del mármol de Tennessee cuidadosamente a diferentes
pero completos ciclos de carga. Donde sus características diferenciables se
identificaron por las propiedades observadas en la pendiente  de la curva deformación-esfuerzo,
inmediatamente antes de que la carga sea liberada.
de la curva deformación-esfuerzo,
inmediatamente antes de que la carga sea liberada.
Para cada muestra de los prismas originales se cortaron consecutivamente, con broca de diamante, cuatro muestras cilíndricas (de 2.5 cm de diámetro y 5.0 cm de longitud) con sus ejes perpendiculares a los ejes longitudinales de las muestras originales, con el objeto de hacer ensayos de tracción directa. Estas muestras cilíndricas se adhirieron a las placas terminales de acero, y sus secciones se redujeron en 5% a lo largo de los 3/4 de sus longitudes. Las placas terminales se atornillaron en su otro extremo a mías barras largas de acero de 0,6 cm de diámetro, y para evitar la aplicación de caigas de flexión sobre las muestras con la máquina de tracción. Muchas de estas muestras sometidas a tracción directa se rompieron transversalmente en su sección reducida, con un cercano plano de clivaje respecto su eje. La Figura 6 muestra, para cada una de estas muestras, la gráfica de los valores de las resistencias a tracción residual respecto la pendiente de la curva deformación-esfuerzo en el estado final de cada ciclo.
Por cada muestra sometida anteriormente a compresión se obtuvieron dos grupos de resistencia a tracción. En cualquier caso, las muestras sometidas a tracción que pertenecen al grupo que obtuvieron altos valores a resistencia residual, provienen de las partes extremas de las muestras que se sometieron inicialmente a compresión. Esta situación puede deberse a dos factores: 1) las fuerzas de fricción entre las placas terminales y la muestra a compresión probablemente proveyeron algún grado de restricción en las partes extremas de las muestras, especialmente durante mía deformación inelástica; 2) las placas rígidas terminales aplicaron una condición constante de deformación a lo ancho de la parte extrema de la muestra, de este modo si mía región débil empezó a fallar, el esfuerzo en ella cayó, mientras que existió mayor libertad para el reajuste en sitios más allá del centro de la muestra, donde una región débil podría continuar fallando. No obstante, parece existir mía relación lineal diferenciable entre la pendiente de la curva deformación-esfuerzo y la resistencia a tracción residual, que puede atribuirse a la extensión de las fisuras durante la carga a compresión original.
También es interesante notar que mientras las resistencias a tracción residual de las muestras cambian por algún orden de magnitud, deberían ser todas lo suficientemente fuertes para aguantar similares cargas máximas.
En la Figura 7 se
gráfica la pendiente de la curva deformación-esfuerzo de la muestra de mármol
de Tennessee respecto los esfuerzos compresivo y axial aplicados para mi ciclo
completo de esfuerzos, seguido por un incremento en el esfuerzo hasta la
rotura. Esta figura realza cómo la pendiente de la curva deformación-esfuerzo
cambia con los esfuerzos aplicados, y muestra cómo la pendiente cambia
súbitamente cuando la carga fue revertida al final del primer
ciclo (Líneas en trazos de la Figura 7).
Las fuerzas de fricción a lo largo de la fisura se revierten cuando la dirección de la carga es revertida y tiene lo suficiente para prevenir el deslizamiento debido a mi cambio pequeño de carga. La pendiente en este punto, probablemente representa el módulo de Young verdadero del mármol de Tennessee. siempre que no estén presentes fisuras o intersticios abiertos a este nivel de esfuerzos ( Walsh. 1965).
Las características deformación-esfuerzo para romper el mármol de Tennessee y el granito de Saint-Cloud se muestran en las Figuras S y 9, respectivamente, juntamente con los registros de la actividad micro-sísmica dibujadas en el mismo eje de abscisas.
En estas figuras se muestran que para el caso del mármol de Tennessee. relativamente homogéneo, la actividad micro-sísmica se limita a una única liberación en un punto, marcado por una caída en la curva deformación-esfuerzo, donde ocurrió una fractura macroscópica temprana (Flecha de la Figura S). En el caso del granito de Saint-Cloud que es relativamente heterogéneo, el incremento de la actividad micro-sísmica precedió a una fractura última.
5. CONCLUSIONES
El lugar geométrico de Griffith que describe el comportamiento inelástico de mía roca fuerte, tiene su origen conforme a un modelo particular de extensión de fisuras. El fundamento básico de la teoría es que la energía potencial elástica se convierte en energía superficial durante la falla de la roca, por un proceso ineficiente de transformación, en donde la energía se disipa por fuerzas de fricción. Pese a que los detalles del modelo prueben que es incorrecto, el análisis se basa bajo aquellos principios energéticos generales, donde el concepto del lugar geométrico de Griffith todavía puede ser válido para describir el comportamiento inelástico.

Figura
8. Curva deformación-esfuerzo y envolvente de actividad micro-sísmica del mármol
de Tennessee Cargada hasta la rotura a compresión.

Figura 9. Curva
deformación-esfuerzo y envolvente de actividad micro-sísmica del granito de
Saint-Cloud Cargada hasta la rotura a compresión.
Los aspectos más
importantes de este concepto son que las cantidades de energía, glandes en
relación a la energía de deformación elástica almacenada, son esencialmente
disipadas durante la falla de la roca: y que la roca fallada retiene resistencia
y cohesión durante la deformación extensiva inelástica. Estos factores son de
vital importancia para comprender cualquier proceso que involucre la falla de
la roca, tales como el proceso de perforación y el fenómeno de
estallido de la roca (i.e rock bursting). Los resultados insuman que para el
proceso de perforación es necesario suministrar mayor energía para fracturar y destruir
la cohesión de la roca, que para esforzar la roca hasta el punto de su falla.
Cualquier solución al problema de estallido de roca probablemente dependerá del
hecho de que glandes cantidades de energía deben ser liberadas por la
excavación subterránea (Cook. 1963) y que pueden ser disipadas por
un proceso de falla estable de la roca.
Agradecimientos
La mayor parte del trabajo presentado en este artículo fue realizado en la Escuela de Ingeniería Minera y Metalúrgica de la Universidad de Minnesota durante el año 1964. con fondos provenientes del Instituto Americano del Petróleo y la Fundación Nacional de la Ciencia. Tengo el placer de agradecer las contribuciones que el señor Crouch hizo para este trabajo experimental
BIBLIOGRAFÍA
[01] Berry J.P.. 1960. Some kinematic considerations of the Griffith criterion for fracture: Equations of motion at constant forcé [Algunas consideraciones cinemáticas del criterio de Griffith para fracturas: Ecuaciones de movimiento a fuerza constante]. J. Mech. Phys Solids. Vol.8. pp. 194-206.
[02] Brace, J.P.. 1960. An extensión of the Griffith theory of fracture to rocks [Una extensión de la teoría de la fractura de Griffith a rocas]. J. Geophys. Res.. Vol.65. pp. 3477-3480.
[03] Cook. N.GW.. 1963. The seismic location of rockburst [La ubicación sísmica del estallido de rocas]. Rock Mech.. Proceedings of the Fifth Rock Mechanics Symposium, Pergamon Press.
[04] Cook. N.G.W.. 1965. A note on rockburst considered as a problem of stability [Anotación sobre el estallido de rocas como problema de estabilidad]. S.A.I.M.M., Vol.65(S). pp. 437.
[05] Mc Clintock. F.A.. Walsh, J.B.. 1962. Friction on Griffith cracks in rock under pressure [ Friction en fisuras tipo Griffith en rocas bajo esfuerzos ]. Proc. 4™ U.S. Nat. Congr. Appl. Mech.. Berkeley pp. 1015-1021.
[06] Muskelishvili, N.I., 1953. Son* basic problems of the mathematical theory of elasticity [Algunos problemas básicos de la teoría matemática de elasticidad]. Translated by J.R.M. Rodak. Noordhof f Croningen. Netherlands. pp. 218-220.
[07] Orowan, E., 1949. Fracture and strength of solids [Fractura y resistencia de los sólidos]. The Physics Society of London. Rep. Progr. Phys. \bL12. pp. 185-232.
[08] Salamon, M.D.G, 1964. Elastic analysis of displacements and stresses induced by mining of Seam or Reef deposits -IV Inclined Reef [Análisis elástico de desplazamientos y esfuerzos inducidos por actividades mineras en veta y de depósitos de «reefs»- IV «Reef» inclinado]. SAIMM, YoL65, pp. 319-338.
[09] Starr, A. 1928. Slip in a cristal and ruptura in a solid due to shear [Deslizamiento en un cristal y ruptura por corte en un sólido]. Proc. Camb. Phil Soc., Vol. 24, pp. 489-500.
[10] Von Karman. X. 1911. Festigkeitversucht unter albreitigem Druk [Estimación de la resistencia bajo presiones]. Z. Ver. Deutsch. Ing.. Vol.55, pp. 1749-1757.
[11] Walsh. J.B.. 1965. The effect of cracks on the compressibility of rock [El efecto de las fisuras en la compresibilidad de la roca]. J. Geophys. Res.. Vol.70. pp. 399-411.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2009 Boletín de Ciencias de la Tierra

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista. Al asumir los derechos patrimoniales del artículo, no podrá reproducirse parcial o totalmente en ningún medio impreso o digital sin permiso expreso del mismo.