Modelado matemático de una enfermedad infecciosa en un centro de reclusión y estrategias óptimas de control preventivo
Palabras clave:
Salud pública, dinámica de población, número básico de reproducción, control de enfermedades transmisibles (fuente, DeCS, BIREME). (es)Se construye un modelo matemático para la dinámica de transmisión y evolución de una enfermedad infecciosa en una cárcel, considerando infecciosos asintomáticos, infecciosos sintomáticos e infecciosos aislados. El modelo se propone como un sistema de ecuaciones diferenciales no lineales que describe los aspectos
epidemiológicos de la dinámica. Se realiza el análisis de estabilidad del modelo para posteriormente incluir en su formulación una estrategia de control preventivo, que permite establecer un protocolo adecuado de control con base en el número básico
de reproducción. Con el fin de minimizar las poblaciones infecciosas y los costos de aplicar la intervención, se formula una funcional de costos ligada al sistema de ecuaciones diferenciales; esta funcional se minimiza mediante el principio del máximo de Pontryagin, lo que permite determinar estrategias óptimas de control preventivo, haciendo mínimas las poblaciones infecciosas y los costos de aplicar la intervención. Luego, se hace un estudio numérico del modelo considerando diferentes niveles de efectividad del control preventivo y diferentes pesos para el control. Finalmente se obtienen las conclusiones del trabajo. El número básico de reproducción caracteriza la estabilidad del modelo y de esta forma, determina criterios claros para su control; se define un umbral de control preventivo con base en el número básico de reproducción con control lo que permite deducir que para controlar la enfermedad es necesaria la aplicación de control preventivo durante todo el tiempo y con altas tasas de efectividad.
Artículos/Investigación
Modelado matemático de una enfermedad infecciosa en un centro de reclusión y estrategias óptimas de control preventivo
Mathematical modelling of an infectious disease in a prison setting and optimal preventative control strategies
Carlos A. Trujillo-Salazar, Hernán D. Toro-Zapata y Aníbal Muñoz-Loaiza
1 Universidad del Quindío. Armenia. Colombia. catrujillo@uniquindio.edu.co; hdtoro@uniquindio.edu.co; amunoz@uniquindio.edu.co.
Recibido 11 de Marzo 2013/Enviado para Modificación 28 Mayo 2013/Aceptado 28 Julio 2013
RESUMEN
Se construye un modelo matemático para la dinámica de transmisión y evolución de una enfermedad infecciosa en una cárcel, considerando infecciosos asintomáticos, infecciosos sintomáticos e infecciosos aislados. El modelo se propone como un sistema de ecuaciones diferenciales no lineales que describe los aspectos epidemiológicos de la dinámica. Se realiza el análisis de estabilidad del modelo para posteriormente incluir en su formulación una estrategia de control preventivo, que permite establecer un protocolo adecuado de control con base en el número básico de reproducción. Con el fin de minimizar las poblaciones infecciosas y los costos de aplicar la intervención, se formula una funcional de costos ligada al sistema de ecuaciones diferenciales; esta funcional se minimiza mediante el principio del máximo de Pontryagin, lo que permite determinar estrategias óptimas de control preventivo, haciendo mínimas las poblaciones infecciosas y los costos de aplicar la intervención. Luego, se hace un estudio numérico del modelo considerando diferentes niveles de efectividad del control preventivo y diferentes pesos para el control. Finalmente se obtienen las conclusiones del trabajo. El número básico de reproducción caracteriza la estabilidad del modelo y de esta forma, determina criterios claros para su control; se define un umbral de control preventivo con base en el número básico de reproducción con control lo que permite deducir que para controlar la enfermedad es necesaria la aplicación de control preventivo durante todo el tiempo y con altas tasas de efectividad.
Palabras clave: Salud pública, dinámica de población, número básico de reproducción, control de enfermedades transmisibles (fuente: DeCS, BIREME).
ABSTRACT
A mathematical model was constructed for modelling transmission dynamics and the evolution of an infectious disease in a prison setting, considering asymptomatic infectious people, symptomatic infectious people and isolated infectious people. The model was proposed as a nonlinear differential equation system for describing disease epidemiology. The model's stability was analysed for including a preventative control strategy which would enable finding a suitable basic reproduction number-based control protocol. A cost function related to the system of differential equations was formulated to minimise infectious populations and intervention costs; such function was minimised by using the Pontryagin maximum principle which determines optimum preventative control strategies by minimising both infectious populations and associated costs. A numerical analysis of the model was made, considering preventative control effectiveness levels and different control weighting constants. Conclusions were drawn. The basic reproduction number characterises system stability and leads to determining clear control criteria; a preventative control threshold was defined, based on the controlled basic reproduction number which enabled deducing that disease control requires uniform preventative control involving high rates of effectiveness.
Key words: Public health, population dynamics, basic reproduction number, communicable disease control (source: MeSH, NLM).
Uno de los delegados médicos del Comité Internacional de la Cruz Roja (CICR) para América Latina, con respecto a los principales problemas en las cárceles, afirma que la situación varía según cada país, pero puede señalarse como una característica común a todos el hacinamiento (1). El caso más dramático de hacinamiento en América Latina se presentó en la prisión de San Juan de Lurigancho, la más grande del Perú. Este sitio fue construido para albergar a 1 500 hombres, pero en 2008 llegó a tener 8 000 recluidos (2). En Colombia, como caso crítico, se tiene la cárcel de Bellavista en Medellín, construida para albergar 1 500 internos, y a la fecha de esta fuente contaba con más de 5 000 (3). Además, la Corte Constitucional colombiana reconoció en 1998, que los niveles de sobrepoblación carcelaria al cerrar la década de los noventa alcanzaban el 40 %, y se sabe que no se ha presentado ninguna mejoría en la última década. Por el contrario, actualmente dicha situación es de extrema gravedad, pues el hacinamiento ha alcanzado un máximo histórico de 41,7 %, evidenciando un déficit de 22 000 cupos (4).
Existe una estrecha relación entre la sobrepoblación carcelaria y las condiciones de salud. Un claro ejemplo es la prisión de Lurigancho, donde se pueden listar las consecuencias del hacinamiento: el acceso regular tanto al agua como a los baños, es inadecuado; las cocinas no son higiénicas; los internos duermen en pasillos y áreas comunes, por falta de espacio en sus celdas; las drogas ilegales son abundantes y el VIH/SIDA ha sido reportado ya en el nivel de epidemia (2). Naturalmente que la situación de Lurigancho se puede generalizar para cualquier cárcel latinoamericana. Y aunque parezca contradictorio, con niveles de hacinamiento altos, la salud deja de ser una prioridad en los presupuestos nacionales penitenciarios porque las autoridades están más concentradas en cuestiones de seguridad y control, como la prevención de fugas e incidentes de violencia. Con frecuencia, la salud penitenciaria tiene un presupuesto insuficiente y una estructura organizacional muy débil (1). Si se analiza nuevamente el caso específico de Colombia, el panorama no es alentador. La Defensoría del Pueblo en el año 2010 presentó un informe sobre la ejecución del decreto 1141 de 2009 (reglamentación de la afiliación de la población reclusa al Sistema General de Seguridad Social en Salud), en el cual manifiesta que la prestación de los servicios de salud en términos de acciones preventivas, terapéuticas y rehabilitadoras son el "talón de Aquiles" del INPEC (Instituto Nacional Penitenciario y Carcelario) y considera además, que es donde se generan graves problemas y se da lugar a vulneraciones de Derechos Humanos en el ámbito carcelario. Más aún, en una de las conclusiones del citado informe, se afirma que solamente un 15 % de los establecimientos penitenciarios y/o carcelarios del país, cuentan con la aprobación en garantía de calidad exigida por el Ministerio de la Protección Social, para prestar servicios de salud en sus áreas de sanidad (5).
De acuerdo con lo anterior, queda en evidencia la delicada situación en materia de salud que se vive al interior de las cárceles colombianas, pero esta no es una problemática aislada. Estas condiciones terminan siendo un problema no sólo para el sistema jurídico sino también para la salud pública (2). En el caso de enfermedades contagiosas, el hecho de que los detenidos estén "olvidados" en los planes nacionales, puede generar un problema de salud pública para toda la población. Desde el punto de vista de la salubridad, las cárceles no son lugares cerrados. No sólo los internos enfrentan un altísimo riesgo de contagio, ya que las enfermedades que se propagan dentro de las cárceles pueden extenderse a la población externa a través de la "población puente", como los liberados, el personal de guardia, el personal administrativo y los visitantes (1).
Claro ejemplo de lo anterior, son algunos estudios en Estados Unidos que manifiestan una preocupación creciente sobre la calidad de la atención médica que los internos reciben cuando están en la cárcel (o la falta de ella), el contagio de enfermedades y la transmisión de las mismas a sus comunidades de origen como resultado de las visitas de familiares o cuando regresan a ellas. Resultado de tales estudios es la existencia de un serio problema de trasmisión de enfermedades como el VIH/SIDA, tuberculosis y la hepatitis C en las cárceles (misma situación que se presenta en el Perú).
En Colombia existen pocos estudios sobre enfermedades específicas en cárceles. En el año 2009 se publicó un estudio sobre infecciones vaginales en las mujeres recluidas en una cárcel colombiana (6). Los estudios generales referentes a las condiciones de salud en las cárceles han estado a cargo de la Defensoría del Pueblo. Un estudio publicado en el año 2003 se hace un diagnóstico y se presentan algunas recomendaciones (7). Otro estudio publicado en el año 2005 presenta nuevamente recomendaciones para la optimización del servicio de salud en las cárceles (3). Como solución a la situación diagnosticada en los anteriores estudios, el 1 de abril del año 2009, se firma el Decreto 1141 que dispone la afiliación de la población reclusa al Sistema General de Seguridad Social en Salud. Y como ya se dijo anteriormente, en el año 2010 se presentó un informe sobre la ejecución de tal decreto, dejando al descubierto muchas fallas en la prestación de los servicios de salud (5). Muy interesante, y como justificación del presente estudio, resulta el hecho de que a pesar de tener un presupuesto aproximado anual general para salud de 14 200 millones de pesos colombianos (8,2 millones de dólares) que cubre atención intramural, atención extramural, medicamentos, promoción y prevención, enfermedades de alto costo y salud mental, parece ser que no es "rentable" para una EPS tener esta población afiliada, tal vez por el perfil epidemiológico de los centros de reclusión (3).
Dada la compleja situación de las cárceles en América Latina, se hace necesario buscar herramientas de análisis que aporten en la toma de decisiones, y en este orden de ideas la modelación matemática es un elemento fundamental de simulación. De acuerdo con lo anterior, en este trabajo se plantea un modelo matemático basado en ecuaciones diferenciales ordinarias para describir la evolución de una enfermedad infecciosa en un ambiente carcelario. Posteriormente se plantea un problema de optimización que tiene por objetivo determinar estrategias óptimas de control de la enfermedad mediante una estrategia de control preventivo para reducir la fuerza de la infección. Y finalmente se presentan algunos resultados numéricos, lo que permite visualizar los resultados analíticos, al tiempo que se validan las estrategias de control determinadas. El modelo es de carácter teórico y por lo tanto, puede ser adaptado a una amplia diversidad de enfermedades infecto-contagiosas de transmisión horizontal como influenza, tuberculosis, SIDA, etc. La bibliografía en el modelado matemático de epidemias es muy amplia, en este documento se incluyen algunos referentes clásicos (8-11).
Planteamiento y análisis del modelo
En la formulación de modelo se considera que la población de la cárcel es constante durante el tiempo de desarrollo de la dinámica; esto puede suponerse porque los egresos balancean los ingresos. La enfermedad se asume que infecta a los reclusos susceptibles por contacto con reclusos infectados. Se supone que la enfermedad presenta dos etapas bien diferenciadas: una asintomática, en la cual no es posible determinar que una persona se encuentra infectada, pero durante la cual es perfectamente posible la transmisión del agente causal de la enfermedad; una segunda etapa inicia cuando aparecen los síntomas de la enfermedad, en este caso el paciente sintomático es fácilmente detectado y puede ser removido bien sea por hospitalización o aislamiento, lo que reduce el tiempo durante el cual es infeccioso. Un supuesto que es coherente en esta situación, es que los reclusos sintomáticos sean más infecciosos que los asintomáticos, principalmente debido a que hacen mayores descargas del agente patógeno.
Se denota con 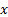 el número promedio de internos susceptibles a la infección, con
el número promedio de internos susceptibles a la infección, con 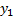 el número promedio de internos infecciosos asintomáticos, con
el número promedio de internos infecciosos asintomáticos, con 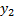 el número promedio de internos infecciosos sintomáticos y
el número promedio de internos infecciosos sintomáticos y 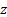 representa el número promedio de internos infecciosos aislados u hospitalizados. Con
representa el número promedio de internos infecciosos aislados u hospitalizados. Con  se representa la población total, de manera que
se representa la población total, de manera que 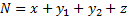 . Los parámetros demográficos y epidemiológicos se describen en la Tabla 1 junto con los valores asignados para la simulación.
. Los parámetros demográficos y epidemiológicos se describen en la Tabla 1 junto con los valores asignados para la simulación.
Se denotan con 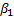 y
y ![]() las tasas de transmisión de la enfermedad. Basados en el principio clásico de "acción de masas" derivado de la reacción de sustancias en Química, se deduce que las expresiones
las tasas de transmisión de la enfermedad. Basados en el principio clásico de "acción de masas" derivado de la reacción de sustancias en Química, se deduce que las expresiones 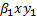 y
y 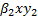 representan el número promedio de individuos susceptibles que se infectan por contacto con infecciosos asintomáticos y sintomáticos, respectivamente. Si se denota con
representan el número promedio de individuos susceptibles que se infectan por contacto con infecciosos asintomáticos y sintomáticos, respectivamente. Si se denota con 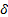 la tasa a la cual los internos ingresan y son liberados de la cárcel, se llega a que la ecuación que describe la variación en el tiempo de la población susceptible es
la tasa a la cual los internos ingresan y son liberados de la cárcel, se llega a que la ecuación que describe la variación en el tiempo de la población susceptible es
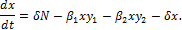
De manera semejante, al asumir que los infecciosos asintomáticos desarrollan la enfermedad y adquieren los síntomas a una tasa  , se tiene que
, se tiene que 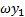 es el número promedio de infecciosos que ingresan a la categoría de sintomáticos; por lo tanto, la variación en el tiempo de la categoría asintomática está dada por
es el número promedio de infecciosos que ingresan a la categoría de sintomáticos; por lo tanto, la variación en el tiempo de la categoría asintomática está dada por
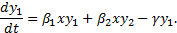
Con 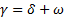 . La variación de los internos en condición sintomática es
. La variación de los internos en condición sintomática es
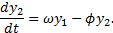
Para  y donde
y donde 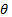 es la tasa de aislamiento de los internos sintomáticos. Finalmente, se tiene que los enfermos aislados presentan la variación descrita por la ecuación diferencial
es la tasa de aislamiento de los internos sintomáticos. Finalmente, se tiene que los enfermos aislados presentan la variación descrita por la ecuación diferencial

Note que la variable 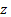 no es necesaria para conocer la dinámica de las otras variables, por tal razón la cuarta ecuación puede ser removida del sistema. Debe ser claro que esta omisión implica que no se podrá saber mucho sobre el comportamiento de la población aislada en el tiempo. Pero dado que el interés principal radica en describir la dinámica de transmisión, no es necesario considerar a
no es necesaria para conocer la dinámica de las otras variables, por tal razón la cuarta ecuación puede ser removida del sistema. Debe ser claro que esta omisión implica que no se podrá saber mucho sobre el comportamiento de la población aislada en el tiempo. Pero dado que el interés principal radica en describir la dinámica de transmisión, no es necesario considerar a 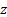 . Bajo este supuesto se llega a que el sistema que interesa es:
. Bajo este supuesto se llega a que el sistema que interesa es:
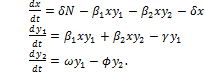 [1]
[1]
Con condiciones iniciales 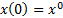 ,
, 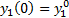 ,
,  .
.
Para verificar que la población de este modelo permanece constante basta con observar que
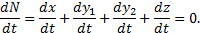
De este modo, puede decirse que 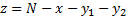 y por lo tanto
y por lo tanto 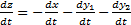 . Expresión que es equivalente a:
. Expresión que es equivalente a:
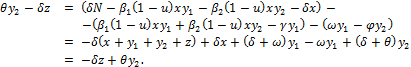
Por lo tanto, la cuarta ecuación del sistema es una identidad y se puede considerar sólo el análisis de las tres primeras ecuaciones.
Proposición 1. El conjunto 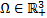 dado por
dado por
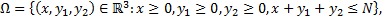
Es positivamente invariante para el sistema [1].
La proposición anterior establece un dominio donde el sistema es matemática y epidemiológicamente razonable, puesto que garantiza que las poblaciones sean siempre positivas y que no crezcan de manera indefinida en el tiempo.
Análisis del modelo
Número básico de reproducción
El número básico de reproducción se define como el número de casos secundarios que un individuo infeccioso es capaz de producir durante su tiempo de infección en una población susceptible, y es determinado mediante el método de la matriz de la siguiente generación, con lo que se tiene el siguiente resultado.
Proposición 2. Para el sistema [1], el número básico de reproducción 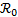 está dado por la expresión
está dado por la expresión
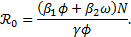
Observe que el 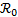 dado en la proposición anterior puede escribirse de la forma
dado en la proposición anterior puede escribirse de la forma
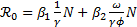 .
.
Note que la expresión 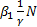 , representa el número promedio de nuevas infecciones producidas por un individuo asintomático durante su periodo infeccioso
, representa el número promedio de nuevas infecciones producidas por un individuo asintomático durante su periodo infeccioso  , en una población susceptible
, en una población susceptible  y con una tasa de infección
y con una tasa de infección 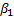 . Del mismo modo
. Del mismo modo 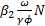 , representa el número promedio de nuevas infecciones producidas por un individuo sintomático durante su periodo infeccioso
, representa el número promedio de nuevas infecciones producidas por un individuo sintomático durante su periodo infeccioso 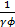 , en una población susceptible
, en una población susceptible  , con una tasa de infección
, con una tasa de infección 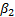 y
y 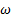 la tasa de evolución de la enfermedad de asintomática a sintomática.
la tasa de evolución de la enfermedad de asintomática a sintomática.
Estabilidad en ausencia de enfermedad
Se puede mostrar que el equilibrio en ausencia de enfermedad está dado por ![]() , lo que indica que la población completa
, lo que indica que la población completa ![]() es susceptible. Es necesario determinar bajo qué condiciones, una perturbación de este equilibrio, como la llegada de un individuo infeccioso, puede resultar en un brote epidémico de la enfermedad.
es susceptible. Es necesario determinar bajo qué condiciones, una perturbación de este equilibrio, como la llegada de un individuo infeccioso, puede resultar en un brote epidémico de la enfermedad.
Proposición 3. Cuando ![]() , el equilibrio libre de enfermedad
, el equilibrio libre de enfermedad ![]() del sistema (1) es globalmente estable.
del sistema (1) es globalmente estable.
Demostración. Sea la función de Lyapunov ![]() . Si
. Si ![]() se tiene
se tiene

El máximo conjunto de invarianza en ![]() es
es ![]() cuando
cuando ![]() . La estabilidad global de
. La estabilidad global de ![]() se sigue del principio de invarianza de La Salle.
se sigue del principio de invarianza de La Salle.
Lo que indica la proposición anterior es que sin importar la magnitud de la perturbación que se haga del estado de equilibrio en ausencia de enfermedad, si ![]() , entonces la infección finalmente desaparece del medio sin lograr establecerse. Es evidente entonces la importancia que
, entonces la infección finalmente desaparece del medio sin lograr establecerse. Es evidente entonces la importancia que ![]() tiene al definir el futuro de la infección.
tiene al definir el futuro de la infección.
Estabilidad en presencia de enfermedad
Para determinar el equilibrio en presencia de infección, se busca una solución no trivial del siguiente sistema algebraico
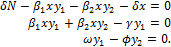
Solución dada por 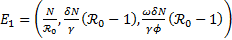 , donde
, donde 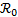 se ha establecido previamente en la proposición 2.
se ha establecido previamente en la proposición 2.
Proposición 4. Si 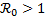 y además
y además 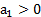 y
y 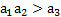 , entonces el equilibrio no trivial
, entonces el equilibrio no trivial 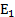 del sistema (1) es local y asintóticamente estable; donde
del sistema (1) es local y asintóticamente estable; donde 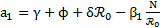 ,
, 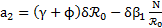 y finalmente
y finalmente 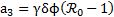 .
.
La proposición establece que dadas esas condiciones se presenta un brote de la enfermedad para finalmente establecerse en el equilibrio 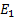 . Esto indica que la enfermedad incursiona en la población y para controlarla es necesaria alguna estrategia.
. Esto indica que la enfermedad incursiona en la población y para controlarla es necesaria alguna estrategia.
Estrategias de control preventivo
En esta sección se introduce en el sistema [1] el control preventivo mediante la cantidad 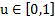 , donde
, donde 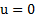 indica que no se aplica ninguna estrategia de control, mientras que
indica que no se aplica ninguna estrategia de control, mientras que 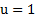 significa que el control preventivo es 100 % efectivo. Entiéndase por control preventivo, cualquier estrategia de control implementada con el fin de disminuir la fuerza de la infección, en particular puede tratarse de vacunación en caso de enfermedades virales, uso de elementos de barrera para enfermedades de transmisión sexual o cualquier otro tipo de medidas preventivas según la enfermedad de interés.
significa que el control preventivo es 100 % efectivo. Entiéndase por control preventivo, cualquier estrategia de control implementada con el fin de disminuir la fuerza de la infección, en particular puede tratarse de vacunación en caso de enfermedades virales, uso de elementos de barrera para enfermedades de transmisión sexual o cualquier otro tipo de medidas preventivas según la enfermedad de interés.
La inclusión del control se hace cambiando los términos 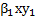 y
y 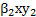 por
por 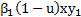 y
y 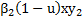 , debido a que si
, debido a que si 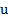 es la efectividad del control,
es la efectividad del control,  representa la falta de efectividad de ese control. De esta manera el sistema (1) asume la forma
representa la falta de efectividad de ese control. De esta manera el sistema (1) asume la forma
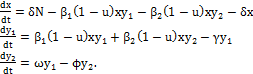 [2]
[2]
Para este nuevo modelo se determina el número básico de reproducción con control, con lo que se obtiene el siguiente resultado.
Proposición 5. Para el modelo [2] el número básico de reproducción con control 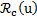 está dado por la expresión
está dado por la expresión
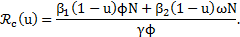
Con base en los resultados de estabilidad de la sección anterior puede deducirse que la enfermedad desaparece del medio cuando 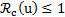 . Despejando
. Despejando 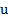 de esta desigualdad se determina la cantidad
de esta desigualdad se determina la cantidad 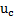 , esto es:
, esto es:
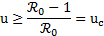
Note que la expresión anterior sólo tiene sentido cuando 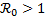 ; es decir, en presencia de la enfermedad. Esto es completamente razonable, ya que solo en presencia de la enfermedad es que se debe hacer inversión en una estrategia de control. Por lo tanto, se puede concluir que cuando el control aplicado tiene una efectividad
; es decir, en presencia de la enfermedad. Esto es completamente razonable, ya que solo en presencia de la enfermedad es que se debe hacer inversión en una estrategia de control. Por lo tanto, se puede concluir que cuando el control aplicado tiene una efectividad 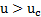 la enfermedad es efectivamente controlada. Luego, se define a
la enfermedad es efectivamente controlada. Luego, se define a 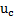 como la estrategia de control preventivo para la infección.
como la estrategia de control preventivo para la infección.
Problema de control óptimo
Se pretende ahora determinar estrategias de control óptimas en el sentido de que se quiere minimizar el costo de aplicar la intervención, al tiempo que se minimizan las poblaciones infecciosas. Para ello, se denota con ![]() el peso asociado con la aplicación del control y se supone que éste es aplicado durante un intervalo de tiempo fijo
el peso asociado con la aplicación del control y se supone que éste es aplicado durante un intervalo de tiempo fijo ![]() . Se define la funcional a minimizar como
. Se define la funcional a minimizar como
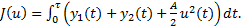 [3]
[3]
Entonces, el objetivo es determinar una función 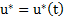 en
en 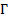 que minimice la funcional
que minimice la funcional 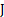 ; en otras palabras, la función
; en otras palabras, la función 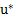 es tal que
es tal que  , para toda
, para toda 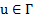 . Donde
. Donde 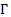 es la clase donde están definidos todos los controles posibles y está dado por
es la clase donde están definidos todos los controles posibles y está dado por  . El límite superior
. El límite superior 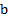 corresponde al valor máximo que puede tomar la efectividad del control
corresponde al valor máximo que puede tomar la efectividad del control 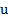 y satisface
y satisface 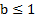 . La funcional
. La funcional 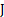 está sujeta al sistema no lineal con control (2). Para determinar el control óptimo
está sujeta al sistema no lineal con control (2). Para determinar el control óptimo 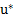 se aplica el Principio del máximo de Pontryagin, una técnica clásica para resolver este tipo de problemas de optimización, con lo que se obtiene el siguiente resultado.
se aplica el Principio del máximo de Pontryagin, una técnica clásica para resolver este tipo de problemas de optimización, con lo que se obtiene el siguiente resultado.
Proposición 6. Para el sistema [2] existe una variable adjunta  que satisface el sistema
que satisface el sistema
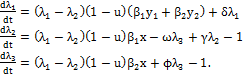 [4]
[4]
Con condiciones finales 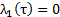 ,
, 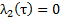 y
y  , y el control óptimo
, y el control óptimo 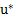 está dado por la expresión
está dado por la expresión
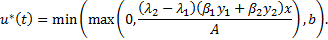
Observe que la proposición anterior establece la forma de calcular la estrategia de control en cada instante 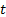 , pero esta depende de que se cuente con las soluciones de los sistemas [2] y [4], lo cual no es posible tener de forma analítica. De este modo, para conocer la función
, pero esta depende de que se cuente con las soluciones de los sistemas [2] y [4], lo cual no es posible tener de forma analítica. De este modo, para conocer la función  es necesario resolver el sistema (2)-(4) con condiciones iniciales
es necesario resolver el sistema (2)-(4) con condiciones iniciales 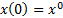 ,
, 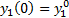 ,
, 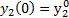 y con condiciones finales
y con condiciones finales 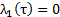 ,
, 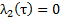 y
y  , donde
, donde 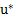 es el dado en la proposición 6.
es el dado en la proposición 6.
Resultados numéricos
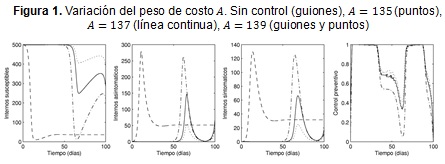
En la Figura 1 se observa que la ausencia de aplicación de control, genera, en un periodo de tiempo muy corto, una reducción drástica del número promedio de internos susceptibles debido a que pasan al estado de infecciosos, tanto asintomáticos como sintomáticos. Aunque con el paso del tiempo tales estados se estabilizan aproximadamente al 10 % y 6 % de la población total, respectivamente, pero en ningún caso se extinguen. En otras palabras, en ausencia de control, el centro de reclusión tendrá permanentemente individuos conviviendo con la enfermedad. Por otro lado, las gráficas dejan ver que la aplicación de un control inicialmente impide la propagación de la enfermedad. Pero al cabo de un tiempo el control preventivo presenta una disminución, ocurrida sin importar el valor del peso ![]() y que alcanza el nivel más bajo a los 60 días aproximadamente. Situación que trae como consecuencia inmediata la disminución de los susceptibles y el incremento de infecciosos. Sin embargo, esta fluctuación es temporal, porque rápidamente los asintomáticos y sintomáticos vuelven a niveles casi nulos. Es importante destacar que las magnitudes de tales brotes y la magnitud del valor de
y que alcanza el nivel más bajo a los 60 días aproximadamente. Situación que trae como consecuencia inmediata la disminución de los susceptibles y el incremento de infecciosos. Sin embargo, esta fluctuación es temporal, porque rápidamente los asintomáticos y sintomáticos vuelven a niveles casi nulos. Es importante destacar que las magnitudes de tales brotes y la magnitud del valor de 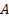 , son directamente proporcionales. Es decir, a menor peso
, son directamente proporcionales. Es decir, a menor peso 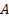 , menor fuerza de la infección. También se observa que el umbral de control preventivo se va aproximando a cero, ocasionando un rebrote, pero esto es consecuencia de la forma en que definieron las condiciones finales del sistema adjunto (4); es decir,
, menor fuerza de la infección. También se observa que el umbral de control preventivo se va aproximando a cero, ocasionando un rebrote, pero esto es consecuencia de la forma en que definieron las condiciones finales del sistema adjunto (4); es decir,  .
.
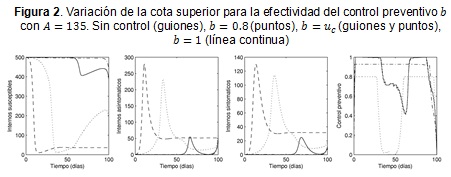
Para analizar la Figura 2 debe tenerse en cuenta que el umbral de control preventivo está dado por 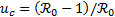 y que bajo los valores de los parámetros de la Tabla 1, asume el valor de
y que bajo los valores de los parámetros de la Tabla 1, asume el valor de 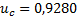 . En primer lugar, se observa entonces la réplica de la situación presentada en ausencia de aplicación de control. En segundo lugar, es evidente que si el valor máximo de la efectividad del control
. En primer lugar, se observa entonces la réplica de la situación presentada en ausencia de aplicación de control. En segundo lugar, es evidente que si el valor máximo de la efectividad del control  es superior o inferior al umbral de control preventivo, se presenta incremento temporal en la población de infecciosos, siendo más tardío y de menor magnitud para el primer caso. Pero si
es superior o inferior al umbral de control preventivo, se presenta incremento temporal en la población de infecciosos, siendo más tardío y de menor magnitud para el primer caso. Pero si 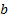 corresponde exactamente al umbral de control preventivo, la población permanece susceptible y no hay lugar a fluctuaciones de la población de infecciosos. Cualquiera que sea el valor de
corresponde exactamente al umbral de control preventivo, la población permanece susceptible y no hay lugar a fluctuaciones de la población de infecciosos. Cualquiera que sea el valor de 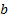 , se presenta una tendencia a cero del control preventivo, generando una disminución en la población susceptible y un incremento en las poblaciones infecciosas (rebrote), pero como se dijo anteriormente, esto obedece a la forma en que se definieron las condiciones finales del sistema adjunto (4); es decir,
, se presenta una tendencia a cero del control preventivo, generando una disminución en la población susceptible y un incremento en las poblaciones infecciosas (rebrote), pero como se dijo anteriormente, esto obedece a la forma en que se definieron las condiciones finales del sistema adjunto (4); es decir,  .
.
- Si el número básico de reproducción es menor o igual a uno
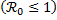 la infección no prospera y no se hace necesaria la aplicación de ningún tipo de control.
la infección no prospera y no se hace necesaria la aplicación de ningún tipo de control. - Cuando
 es evidente la necesidad de la aplicación permanente de un control preventivo con altas tasas de efectividad, pues de lo contrario los brotes de la infección son inevitables.
es evidente la necesidad de la aplicación permanente de un control preventivo con altas tasas de efectividad, pues de lo contrario los brotes de la infección son inevitables. - Si el valor máximo de la efectividad del control
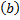 coincide con el umbral de control preventivo
coincide con el umbral de control preventivo 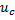 , la estrategia de control es mucho más uniforme en el tiempo y evita la aparición de brotes de la infección.
, la estrategia de control es mucho más uniforme en el tiempo y evita la aparición de brotes de la infección.
REFERENCIAS
1. Comité Internacional de la Cruz Roja [Internet]. Disponible en: http://www.icrc.org/web/spa/sitespa0.nsf/html/paraguay-interview-030309. Consultado en enero de 2013.
2. Pérez L. Cuando las enfermedades salen libres. Ideele. 2008; N° 187: 86-87.
3. Defensoría del Pueblo de Colombia. Defensoría delegada para la política criminal y Penitenciaria. Informe sobre prestación de servicios de salud en centros penitenciarios y carcelarios de Colombia. Santa Fé de Bogotá; 2005.
4. Ministerio del Interior y de Justicia de la República de Colombia. Del encarcelamiento a la efectiva resocialización. Foro "Estado de cosas inconstitucional en las prisiones colombianas. Sentencia T-153 de 1998". Universidad de los Andes. Bogotá; 12 de marzo de 2010.
5. Defensoría del Pueblo de Colombia. Defensoría delegada para la política criminal y Penitenciaria. Informe sobre ejecución decreto 1141 de 2009. Santa Fé de Bogotá; 2010.
6. López-Barbosa N, Castro-Jiménez MA, Gamboa-Delgado EM, Vera-Cala ML. Prevalencia y determinantes de las infecciones vaginales en las mujeres recluidas en una cárcel colombiana. Rev. Chil. Obstet. Ginecol. 2009; 74(2):77-82.
7. Defensoría del Pueblo de Colombia. Situación del servicio de salud en las cárceles de Colombia. Santa Fé de Bogotá; 2003.
8. Chowel G, Diaz-Dueñas P, Miller JC, Alcazar-Velazco A, Hyman JM, Fenimore PW, et al. Estimation of the reproduction number of dengue fever from spatial epidemic data. Mathematical Biosciences. 2007; 208:571-589.
9. Greenhalgh D. Some results on optimal control applied to epidemics. Mathematical Biosciences. 1986; 88:125-158.
10. Anderson RM. The populations dynamics of infectius diseases: Theory and applications. New York: Chapman and Hall; 1982.
11. Bailey NTJ. The mathematical theory of infectious diseases. New York: Hafner Press; 1957.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2013 Revista de Salud Pública

Esta obra está bajo una licencia internacional Creative Commons Atribución 4.0.
Esta revista provee acceso libre inmediato a su contenido bajo el principio de que hacer disponible gratuitamente investigación al publico apoya a un mayor intercambio de conocimiento global.
Todos los contenidos de esta revista, excepto dónde está identificado, están publicados bajo una Licencia Creative Commons Atribución 4.0.