SELECCIÓN DE UN MODELO CÓPULA PARA EL AJUSTE DE DATOS BIVARIADOS DEPENDIENTES

El modelamiento en problemas que involucran datos bivariados dependientes es muy importante en diversas áreas del conocimiento, tales como: finanzas, actuaría, confiabilidad y análisis de supervivencia. En la literatura, se conocen algunos modelos cópula que han sido ampliamente utilizados para modelar distribuciones multivariadas dependientes, entre los cuales se destaca la clase de cópulas Arquimedianas. En este artículo, se presenta una metodología para seleccionar entre algunos modelos cópula Arquimedianos el que mejor se ajusta a un conjunto de datos dependientes, utilizando gráficos de bondad de ajuste, gráficos cuantil cuantil (Q-Q plot) y la prueba analítica de bondad de ajuste de Cramér-von Mises. Se realizó una aplicación de la metodología con datos simulados y utilizando datos de siniestros en pólizas de seguro. Los resultados mostraron que los datos de seguros se ajustan a un modelo bivariado basado en la cópula Frank con marginales lognormales.

SELECTION OF A COPULA MODEL TO FIT BIVARIATE DEPENDENT DATA

CARLOS MARIO LOPERA
Escuela de Estadística, Universidad Nacional de Colombia, Profesor Asistente, cmlopera@unal.edu.co

MARIO CÉSAR JARAMILLO
Escuela de Estadística, Universidad Nacional de Colombia, Profesor Asociado, mcjarami@unal.edu.co

LUIS DAVID ARCILA
Suramericana de Seguros S.A, Director de Actuaría, luisarho@suramericana.com.co

Recibido para revisar junio 11 de 2008, aceptado noviembre 2 de 2008, versión final noviembre 13 de 2008

---

RESUMEN: El modelamiento en problemas que involucran datos bivariados dependientes es muy importante en diversas áreas del conocimiento, tales como: finanzas, actuaría, confiabilidad y análisis de supervivencia. En la literatura, se conocen algunos modelos cópula que han sido ampliamente utilizados para modelar distribuciones multivariadas dependientes, entre los cuales se destaca la clase de cópulas Arquimedianas. En este artículo, se presenta una metodología para seleccionar entre algunos modelos cópula Arquimedianos el que mejor se ajusta a un conjunto de datos dependientes, utilizando gráficos de bondad de ajuste, gráficos cuantil cuantil (Q-Q plot) y la prueba analítica de bondad de ajuste de Cramér-von Mises. Se realizó una aplicación de la metodología con datos simulados y utilizando datos de siniestros en pólizas de seguro. Los resultados mostraron que los datos de seguros se ajustan a un modelo bivariado basado en la cópula Frank con marginales lognormales.

PALABRAS CLAVE: Modelos Cópula, Distribución bivariada dependiente, Gráficos de bondad de ajuste, Gráficos cuantil cuantil, Pruebas de bondad de ajuste.

ABSTRACT: Modeling problems involving bivariate dependent data is very important in many areas, such as finance, actuary, reliability and survival analysis. In the literature, some copula models have been widely used to modelling dependent multivariate distributions, among which stands out the Archimedean copula class. This paper presents a methodology to select from some Archimedean copula models the one that fits the best to a dependent dataset, using goodness-of-fit plots, Q-Q plots and Cramér-von Mises goodness-of-fit test. We illustrated the methodology using simulated data and data from insurance claims. The results showed that the data insurance fits to a bivariate model based on the so called Frank's copula with lognormal marginals.

KEYWORDS: Copula models, Dependent bivariate distribution, Goodness-of-fit plot, Q-Q plot, Goodness-of-fit test.

---

1. INTRODUCCIÓN

Las cópulas se han convertido en una potente herramienta para el modelamiento multivariado en muchos campos donde la dependencia multivariada es de gran interés. En actuaría, las cópulas son usadas en el modelamiento de mortalidad y las pérdidas dependientes [1-3]. En finanzas, las cópulas son usadas en asignación de activos, modelamiento y administración de riesgos, calificación de créditos y tasación derivada [4-6]. En estudios biomédicos, las cópulas son usadas en el modelamiento de tiempos de eventos correlacionados y competing risks [7-8]. En ingeniería, las cópulas son usadas en el control de procesos multivariados y en el modelamiento hidrológico [9-10]. Las cópulas son de gran utilidad en la generación de datos divariados dependientes [11].

Investigaciones recientes se han centrado en una clase de cópulas llamada cópulas arquimedianas, la cual agrupa varias familias de modelos cópula, con propiedades analíticas más sencillas. Muchas distribuciones bivariadas conocidas pertenecen a la clase de cópulas Arquimedianas. Los modelos de fragilidad también hacen parte de esta clase. En la referencia [12] se ilustran que esta clase de cópulas es amplia, analíticamente sencilla y sus elementos tienen propiedades estocásticas que los hacen atractivos para el tratamiento estadístico de los datos. Además, las cópulas Arquimedianas pueden describir una gran diversidad de estructuras de dependencia [13].

El principal inconveniente cuando se quiere modelar datos bivariados dependientes utilizando modelos cópula, es que no hay ningún indicio de cuál es la forma paramétrica de la cópula. Por lo tanto, para proceder con un análisis paramétrico tradicional se debe asumir una forma funcional para la cópula. Aunque muchas formas funcionales se han sugerido [14], no hay una guía general para la selección óptima de una cópula. Hasta ahora hay pocos estudios que tratan de abordar el problema. En la referencia [15] se investigó si datos bivariados dependientes pueden ser descritos por la cópula Gaussiana. En la referencia [16] se consideró el análisis multivariado de datos para probar la hipótesis de la cópula Gaussiana y Student.

El objetivo de este artículo es difundir una metodología para la selección de un modelo cópula Arquimediano que ajuste bien a un conjunto de datos bivariados dependientes. Si bien la metodología presentada no es óptima, en el sentido de que para un caso particular puede seleccionarse más de una cópula que ajuste bien los datos, se tiene un procedimiento sencillo que puede contribuir en una amplia gama de problemas prácticos. La selección del modelo cópula se basará en la utilización de gráficos de bondad de ajuste, gráficos cuantil-cuantil y el estadístico de Cramér-von Mises.

En la Sección 2, se presenta una descripción básica de los modelos cópula, la cual pretende dar un marco de referencia para el trabajo en las secciones posteriores. La Sección 3, presenta la forma en que se lleva a cabo la selección de un modelo cópula Arquimediano para ajustar un conjunto de datos, con ilustración de la metodología con datos simulados. En la Sección 4, se presenta una aplicación con datos reales en el campo de la actuaría. Finalmente, algunas conclusiones y recomendaciones están dadas en la sección 5.

2. DESCRIPCIÓN DEL MODELO CÓPULA

Suponga que es una función de distribución con densidad sobre para 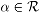. Denote las dos variables aleatorias, y denote las respectivas funciones de distribución y densidad marginales. Si proviene de una cópula para algún , entonces las funciones de distribución y densidad conjuntas de están dadas por

donde representa el parámetro de dependencia entre las variables y 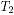.Dos de las clases de cópulas más usadas son las cópulas elípticas y las Arquimedianas. Para mayor detalle de las clases de cópulas, [5]. A continuación se introduce la clase de cópulas Arquimedianas, ya que ésta se puede simular fácilmente y los cálculos de medidas de dependencia se simplifican, lo cual permite una mejor estimación de los parámetros. Adicionalmente, las cópulas Arquimedianas describen una gran diversidad de estructuras de dependencia [13].

2.1 Cópulas Arquimedianas
Una distribución bivariada perteneciente a la clase de modelos cópula Arquimedianos tiene la representación

donde es convexa y decreciente tal que . A la función se le denomina generador de la cópula y la inversa del generador es la transformada de Laplace de una variable latente denotada , la cual induce la dependencia . Así, la selección de un generador resulta en varias familias cópula. En la Tabla 1, se muestran las formas funcionales para las funciones de distribución bivariadas en cuatro de las familias cópula Arquimedianas resultantes. Adicionalmente, en las Tablas 2 y 3, se muestran los generadores, las transformadas de Laplace y la relación entre el parámetro y el coeficiente de correlación de Kendall, para las familias consideradas.

Tabla 1. Cópulas Arquimedianas
Table 1. Archimedean copulas

Tabla 2. Generadores y transformadas de Laplace de las cópulas Arqui­medianas
Table 2. Generators and Laplace transform of Archimedean copulas.

Tabla 3. de Kendall de las cópulas Arqui­medianas
Table 3. Kendall’s of Archimedean copulas

A continuación se dan detalles de las familias cópulas Arquimedianas consideradas.

2.1.1 Familia Clayton
La función de distribución bivariada perteneciente a la familia Clayton [17] tiene la forma

Aquí es la transformada de Laplace de una distribución gama. y 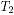están positivamente asociados cuando y son independientes cuando . Denote la función hazard. En la referencia [17] se mostró que , si y sólo si, la función de confiabilidad bivariada pertenece a la familia Clayton.

2.1.2 Familia Gumbel
La función de confiabilidad bivariada perteneciente a la familia Gumbel [18] tiene la forma

donde, . Aquí es la transformada de Laplace de una distribución estable positiva. Valores pequeños de producen alta correlación y , 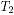son independientes cuando .

2.1.3 Familia Frank
La función de confiabilidad bivariada introducida por Frank [19] tiene la representación

donde . y 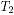están asociados positivamente cuando 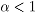, negativamente cuando , y son independientes cuando .

Aquí ­ y se convierte en una transformada de Laplace cuando .

2.1.4 Familia Joe
La función de confiabilidad bivariada perteneciente a la familia Joe [20] tiene la forma

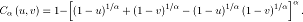
Aquí 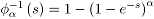es la transformada de Laplace asociada.

3. METODOLOGÍA PARA LA SELECCIÓN DE UN MODELO CÓPULA ARQUIMEDIANO

Suponga que se tiene una muestra aleatoria de observaciones bivariadas que se presumen dependientes , , 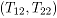, . Asuma que la función de distribución conjunta tiene asociada una cópula Arquimediana , y esta a su vez tiene asociado un generador . Entonces, el objetivo es lograr identificar entre las familias cópula Arquimedianas expuestas en la sección 2.1, cuál o cuáles de ellas ajustan mejor la distribución conjunta de y 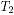. Para elegir la familia cópula que mejor se ajusta se debe primero identificar la función generadora de la misma . Para ello en [21] definieron las variables aleatorias no observables 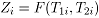, que tienen función de distribución acumulada . Ellos mostraron que:

Luego, el siguiente procedimiento ayuda en la identificación de :

1. Estimar para la muestra el coeficiente de correlación de Kendall, y llámelo .

2. Construir una estimación no paramétrica de como sigue:

Defina las seudo observaciones

para .

Construya la estimación de como:

3. Construir una estimación paramétrica de usando (6), así:

para varias escogencias de la función .

Para ello, estime , usando la estimación del paso 1 y la relación existente entre ambos explicada en Tabla 2; llame a este valor . Luego, use este valor para estimar en Tabla 2, y llámelo . Finalmente, use para estimar , y llámelo .

4. Construir el gráfico de bondad de ajuste para las dos funciones de distribución estimadas de la variable (la estimación empírica y asumiendo un generador para la función cópula) y el gráfico de cuantil cuantil, donde se comparan los cuantiles empíricos con aquellos asociados a un modelo cópula paramétrico. Adicionalmente, se pueden realizar pruebas analíticas de bondad de ajuste entre las funciones y .

Se repiten los pasos 3 y 4 para varias escogencias del generador . Finalmente, de acuerdo a los gráficos y pruebas realizadas en el paso 4, se escoge el modelo cópula cuya estimación paramétrica de se acerque más a la estimación no paramétrica de dicha función.

A continuación se ilustra el procedimiento de identificación de una función cópula para datos bivariados dependientes. Como el objetivo de este ejercicio es comprobar la identificación correcta de un modelo cópula, entonces se asumirá en cada caso un modelo cópula que vincula las distribuciones marginales con una distribución bivariada, las cuales se toman de manera arbitraria.

En todos los casos se generaron muestras () de tamaño n = 1000, correspondientes a datos bivariados dependientes (se tomó un valor para el coeficiente de correlación de Kendall de , que representa una alta dependencia positiva), con las siguientes características:

• Caso 1: y , donde los parámetros de la distribución lognormal son y respectivamente. Se asumirá el modelo cópula Clayton para generar la distribución bivariada.
• Caso 2: y . Se asumirá el modelo cópula Frank para generar la distribución bivariada.
• Caso 3: y . Se asumirá el modelo cópula Gumbel para generar la distribución bivariada.

En cada caso se realizan gráficos de bondad de ajuste de las estimaciones de la distribución empírica y paramétrica, gráficos de cuantil cuantil y pruebas de bondad de ajuste de Cramér-von Mises (para detalles de esta prueba, [22]). Los resultados se dan a continuación.

En los resultados obtenidos para el Caso 1, es decir, para datos generados utilizando una cópula Clayton para vincular las distribuciones marginales con una distribución bivariada dependiente, el mejor ajuste se observa cuando se trabaja la cópula Clayton que es lo que se esperaba. Esto se indica por la cercanía de las curvas en la Figura 1, la superposición de los puntos de dispersión de los cuantiles empíricos y los cuantiles Clayton, con la recta imagen en la Figura 2, y en los valores-p de las pruebas analíticas de bondad de ajuste en la Tabla 4. En esta última se observa que el único valor-p que lleva a aceptar la hipótesis de igualdad de las distribuciones empírica y paramétrica se da para el modelo cópula Clayton. En todos los análisis que se realizan de aquí en adelante se utiliza un nivel de significancia del 5%.

Figura 1. Comparación de las distribuciones empírica y paramétrica para el Caso 1
Figure 1. Comparison of empirical and parametric distributions for Case 1

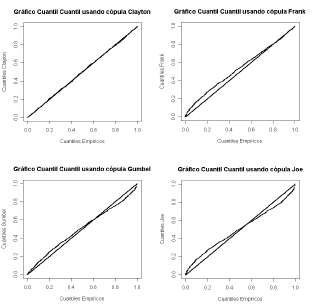
Figura 2. Gráficos Cuantil Cuantil para el Caso 1
Figure 2. Q-Q plots for Case 1

Tabla 4. Pruebas analíticas de bondad de ajuste para el caso 1
Table 4. Goodness-of-fit tests for Case 1

En los resultados obtenidos para el Caso 2, es decir, para datos generados utilizando una cópula Frank para vincular las distribuciones marginales con una distribución bivariada dependiente, el mejor ajuste se observa cuando se trabaja la cópula Frank que es lo que se esperaba. Esto se indica por la cercanía de las curvas en la Figura 3, la cercanía de los puntos de dispersión de los cuantiles empíricos y los cuantiles Frank, con la recta imagen en la Figura 4, y en los valores-p de las pruebas analíticas de bondad de ajuste en la Tabla 5. En esta última se observa que si bien los modelos cópula Frank, Gumbel y Joe aceptan la hipótesis de igualdad de las distribuciones empírica y paramétrica, el mayor valor-p se da para el modelo cópula Frank, lo que indica que bajo este modelo se tiene el mejor ajuste.

Figura 3. Comparación de las distribuciones empírica y paramétrica para el Caso 2
Figure 3. Comparison of empirical and parametric distributions for Case 2

Figura 4. Gráficos Cuantil Cuantil para el Caso 2
Figure 4. Q-Q plots for Case 2

Tabla 5. Pruebas analíticas de bondad de ajuste para el Caso 2
Table 5. Goodness-of-fit tests for Case 2

En los resultados obtenidos para el Caso 3, es decir, para datos generados utilizando una cópula Gumbel para vincular las distribuciones marginales con una distribución bivariada dependiente, el mejor ajuste se observa cuando se trabaja la cópula Gumbel que es lo que se esperaba. Esto se indica por la cercanía de las curvas en la Figura 5, la superposición de los puntos de dispersión de los cuantiles empíricos y los cuantiles Gumbel, con la recta imagen en la Figura 6, y en los valores-p de las pruebas analíticas de bondad de ajuste en la Tabla 6. En esta última se observa que aunque los valores-p asociados a las cópulas Clayton, Gumbel y Joe llevan a aceptar la hipótesis de igualdad de las distribuciones empírica y paramétrica, el mayor de estos valores-p se da para el modelo cópula Gumbel, de manera que como se esperaba esta cópula ofrece el mejor ajuste para los datos.

Tabla 6. Pruebas analíticas de bondad de ajuste para el Caso 3
Table 6. Goodness-of-fit tests for Case 3

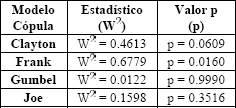
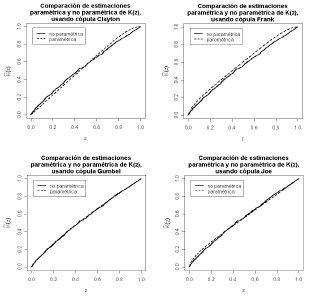
Figura 5. Comparación de las distribuciones empírica y paramétrica para el Caso 3
Figure 5. Comparison of empirical and parametric distributions for Case 3

Figura 6. Gráficos Cuantil Cuantil para el Caso 3
Figure 6. Q-Q plots for Case 3

La implementación de las simulaciones anteriores se realizó utilizando el software estadístico R, versión 2.6.2 [23]. El código utilizado se suministra bajo pedido a los autores.

4. APLICACIÓN EN PÓLIZAS DE SEGUROS

Los datos corresponden a 478 valores pagados en millones de pesos por siniestros, sobre los cuales fueron cargados gastos asociados a los mismos en pólizas de seguro de propiedad de la compañía Suramericana de Seguros S.A., dichos valores fueron obtenidos durante los años 2005 a 2007.

La póliza de seguro analizada corresponde a un producto diseñado para proteger el hogar y los bienes del asegurado. La cobertura básica comprende la indemnización del valor de reconstrucción o de reposición a nuevo de los bienes que se vean afectados por cualquiera de los siguientes eventos: Incendio y/o Rayo, Explosión, Granizo, Anegación y Daños por Agua, Huracán y Vientos Fuertes, Tifón, Ciclón y Tornado, Caída de Aeronaves o de Objetos que se Desprendan o Caigan de Ellas, Impacto de Vehículos Terrestres, Humo, Asonada, Motín, Conmoción Civil o Popular y Huelga (según definiciones de ley), Actos Mal Intencionados de Terceros (AMIT), Gastos por Remoción de Escombros, Actos de Autoridad, Honorarios Profesionales, Gastos de Extinción del Siniestro y Gastos para la Preservación de Bienes.

A continuación en la Tabla 7, se presentan los estadísticos de resumen de las variables descritas anteriormente.

Tabla 7. Estadísticos resumen de los datos de pólizas de seguros
Table 7. Summary statistics of the data of insurance claims

Es de interés investigar la distribución conjunta de los pagos y gastos de seguros, para lo cual se utilizarán las representaciones cópula estudiadas y entre ellas se escogerá mediante las pruebas de bondad de ajuste gráficas y analíticas vistas en sección 3, la cópula que ofrezca el mejor ajuste a los datos. Las figuras 7 y 8 y la Tabla 8 muestran los resultados obtenidos de la selección del modelo cópula.

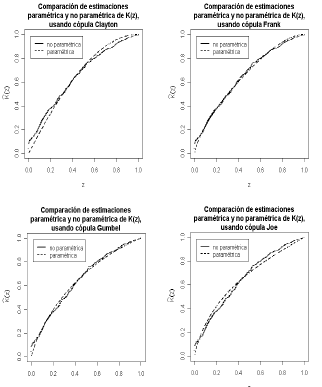
Figura 7. Comparación de las distribuciones empírica y paramétrica para los datos de seguros
Figure 7. Comparison of empirical and parametric distributions for the insurance data

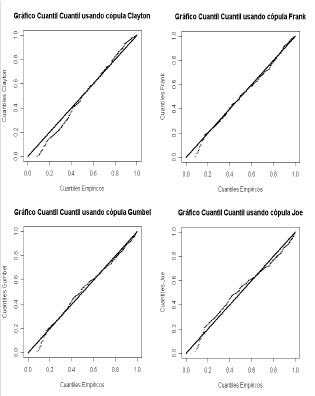
Figura 8. Gráficos Cuantil Cuantil para los datos de seguros
Figure 8. Q-Q plots for insurance data

Tabla 8. Pruebas analíticas de bondad de ajuste para los datos de seguros
Table 8. Goodness-of-fit tests for insurance data

Como se observa en los análisis anteriores la cópula que mejor ajusta la distribución conjunta de los datos de pagos y gastos en pólizas de seguros es la cópula Frank, cuyo valor estimado del parámetro es .

Identificada la cópula el analista puede estar interesado en realizar el ajuste por máxima verosimilitud de los parámetros de la distribución bivariada generada por ella. Para más detalles de cómo se hace el ajuste, [1].

La estimación puede utilizarse para realizar cálculos de probabilidades en la distribución bivariada, por ejemplo, calcular la probabilidad de que los pagos y gastos en pólizas de seguros superen valores específicos.

A continuación se ilustrará el procedimiento de ajuste para los datos de seguros.

El primer paso consiste en ajustar las distribuciones marginales utilizando el estadístico de Kolmogorov-Smirnov donde los parámetros de cada una de las distribuciones se estimaron mediante máxima verosimilitud. Se utilizan las cuatro distribuciones univariadas más comunes para estos tipos de datos.

De la Tabla 9 se puede concluir que ambas variables Pagos y Gastos en pólizas de seguros se distribuyen Lognormal.

Tabla 9. Pruebas de bondad de ajuste para distribuciones marginales
Table 9. Goodness-of-fit tests for distributions marginals

Con esta información se procede a la estimación por máxima verosimilitud de los parámetros de la cópula. La Tabla 10 muestra los resultados de este procedimiento.

Tabla 10. Parámetros estimados de la distribución bivariada
Table 10. Parameter estimates of the bivariate distribution

Comparando las estimaciones de máxima verosimilitud para las distribuciones marginales univariadas y la distribución bivariada se observan cambios muy leves en estos valores. El parámetro de dependencia estimado para la cópula Frank usada en este análisis indica que las variables Pagos y Gastos en pólizas de seguros no son independientes y de acuerdo a la Tabla 3, este corresponde a un valor del coeficiente de correlación de Kendall de 0.3985 que indica una correlación positiva entre estas variables.

5. CONCLUSIONES Y RECOMENDACIONES

Las cópulas se destacan como una herramienta sencilla y útil para la construcción de distribuciones bivariadas dependientes que explique el comportamiento de un conjunto de datos.

La familia de cópulas Arquimediana presenta una gran versatilidad en la descripción de conjuntos de datos bivariados dependientes, esto se evidencia en el sentido de que pueden existir varios modelos Arquimedianos que ajusten en buena medida un conjunto de datos específico.

Para la selección de un modelo cópula bivariado dependiente, se resalta la utilización de herramientas gráficas muy conocidas y de fácil implementación en paquetes estadísticos. Esto permite que los analistas puedan de una manera ágil y clara identificar un modelo cópula para la construcción de una distribución bivariada dependiente que ajuste bien un conjunto de datos.

La metodología presentada permite identificar la estructura y el grado de dependencia presente en datos reales bivariados, lo cual sugiere que en problemas reales siempre se debe suponer dependencia entre las variables, en lugar de trabajar bajo el supuesto de independencia, que es una práctica común en el análisis de este tipo de datos.

En la construcción de distribuciones bivariadas dependientes usando cópulas no se requiere que las distribuciones marginales sean del mismo tipo. Esto muestra la versatilidad de la metodología para la construcción de distribuciones bivariadas dependientes en problemas prácticos. Sin embrago, en la aplicación con datos de pólizas de seguros se obtuvieron ambas marginales lognormales.

6. AGRADECIMIENTOS

Los autores agradecen de manera muy especial al Profesor Juan Carlos Salazar Uribe de la Escuela de Estadística de la Universidad Nacional, por su asesoría, apoyo y colaboración en este trabajo.

REFERENCIAS

[1] FREES, E. W. AND VALDEZ, E. A., Understanding Relationships Using Copulas, North American Actuarial Journal 2(1), 1-25, 1998.
[2] FREES, E. W. AND WANG, P., Credibility Using Copulas, North American Actuarial Journal 9(2), 31-48, 2005.
[3] FREES, E. W., CARRIÉRE, J. F. AND VALDEZ, E. A., Annuity Valuation with Dependent Mortality, Journal of Risk and Insurance 63, 229-261, 1996.
[4] BOUYÉ, E., DURRLEMAN, V., BIKEGHBALI, A., RIBOULET, G. AND RCONCALLI, T., Copulas for Finance - A Reading Guide and Some Applications, Manuscript, Financial Econometrics Research Center, 2000.
[5] EMBRECHTS, P., LINDSKOG, F. AND Mcneil, A., Modelling Dependence with Copulas and Applications to Risk Management. En Rachev, S. (Ed.), Handbook of Heavy Tailed Distribution in Finance, first edn, Elsevier, North-Holland, 2003.
[6] CHERUBINI, U., LUCIANO, E. AND Vecchiato, W., Copula Methods in Finance, first edn, John Wiley & Sons, New York, 2004.
[7] WANG, W. AND WELLS, M. T., Model Selection and Semiparametric Inference for Bivariate Failure-Time Data, Journal of the American Statistical Association 95, 62-72, 2000.
[8] ESCARELA, G. AND CARRIÉRE, J. F., Fitting Competing Risks with an Assumed Copula, Statistical Methods in Medical Research 12(4), 333-349, 2003.
[9] YAN, J., Multivariate Modeling with Copulas and Engineering Applications. In Pham, H. (Ed.), Handbook in Engineering Statistics, first edn, Springer, New York, 2006.
[10] GENEST, C. AND FAVRE, A. C., Everything You Always Wanted to Know About Copula Modeling but were Afraid to Ask, Journal of Hydrologic Engineering 12(4), 347-368, 2007.
[11] MANOTAS, E., YÁÑEZ, S., LOPERA, C. AND JARAMILLO, M., Estudio del Efecto de la Dependencia en la Estimación de la Confiabilidad de un Sistema con Dos Modos de Falla Concurrentes, DYNA 75(154), 29-38, 2008.
[12] GENEST, C. AND Mackay, R. J., Copules archimédiennes et familles de lois bidimensionnelles dont les marges sont données, Canadian Journal of Statistics 14(2), 145-159, 1986.
[13] EVIN, G., FAVRE, A. C. AND GENEST, C., Comparison of goodness-of-fit tests adapted to copulas, Geophysical Research Abstracts, 2005.
[14] NELSEN, R. B., An Introduction to Copulas, second edn, Springer, New York, 2006.
[15] MALEVERGNE, Y. AND SORNETTE, D., Testing the Gaussian copula hypothesis for financial assets dependences, Quantitative Finance 3, 231-250, 2003.
[16] PATTON, A. J., CHEN, X. AND FAN, Y., Simple Tests for Models of Dependence Between Multiple Financial Time Series, with Applications to U.S. Equity Returns and Exchange Rates, Discussion Paper 483, Financial Markets Group, London School of Economics, 2004.
[17] CLAYTON, D. G., A Model for Association in Bivariate Life Tables and its Application in Epidemiological Studies of Familial Tendency in Chronic Disease Incidence, Biometrika 65, 141-152, 1978.
[18] GUMBEL, E. J., Bivariate Exponential Distributions, Journal of the American Statistical Association 55, 698-707, 1960.
[19] FRANK, M. J., On the Simultaneous Associativity of f(x,y) and x + y - f(x,y), Aequationes Mathematicae 19, 194-226, 1979.
[20] JOE, H., Parametric Family of Multivariate Distributions con Margins Given, Journal of Multivariate Analysis 46, 262-282, 1993.
[21] GENEST, C. AND RIVEST, L., Statistical Inference Procedures for Bivariate Archimedean Copulas, Journal of the American Statistical Association 88(423), 1034-1043, 1993.
[22] CONOVER, W. J., Practical Nonparametric Statistics, third edn, John Wiley & Sons, New York, 1999.
[23] R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria . Available: http://www.R-project.org [citado 8 de junio de 2008].