MODELADO DE LA OSIFICACIÓN DE LAS EPÍFISIS DE HUESOS LARGOS
Palabras clave:
Centros secundarios de osificación, morfogénesis del hueso, procesos de reacción-difusión, simulación en elementos finitos. (es)MODELADO DE LA OSIFICACI ÓN DE LAS EPÍFISIS DE HUESOS LARGOS
MODELING OF EPYPHISIS OSSIFICATION IN LONG BONES
D. A. GARZÓN -
ALVARADO
Grupo de Modelado Matemático y
Métodos Numéricos en Ingeniería -GNUM, Universidad Nacional de Colombia dagarzona@unal.edu.co
Recibido para revisar agosto 12 de 2008, aceptado junio 12 de 2009, versión final junio 22 de 2009
RESUMEN: Se presenta en este documento un modelo matemático de hipertrofia de condrocitos, regulado por factores moleculares capaces de predecir la aparición y localización de los centros secundarios de osificación durante el desarrollo de los huesos largos. De los resultados obtenidos, concluimos que la retroalimentación (bucle) química entre dos factores moleculares reactivos a través de un mecanismo de reacción-difusión podría explicar el patrón espacial estable encontrado en el origen de los centros secundarios de osificación, así como también la dependencia de dicho patrón en el tamaño y forma de la cabeza del hueso, según lo observado en diferentes animales.
PALABRAS CLAVE: Centros secundarios de osificación, morfogénesis del hueso, procesos de reacción-difusión, simulación en elementos finitos.
ABSTRACT: We present here a mathematical model of chondrocytes hypertrophy, regulated by molecular factors, able to predict the onset of secondary ossification centers during long bones development. From the results obtained, we can conclude that the chemical feedback between two reactive molecular factors through a reaction-diffusion mechanism could explain the stable spatial pattern found in the origination of secondary ossification centers, as well as the dependency of such a pattern on the size and shape of the bone head, in line with what has been observed in different animals.
KEYWORDS: Secondary ossification centre, bone morphogenesis, reaction-diffusion process, finite element simulation.
1. INTRODUCCIÓN
La morfogénesis de tejidos biológicos es el resultado de interacciones complejas entre la evolución de las especies y su adaptación individual al medio [1]. Las células son los principales actores de tales eventos, desempeñando una serie de procesos coordinados, entre los que se destacan la proliferación, diferenciación, migración, apoptosis y producción de tejido. Estos procesos son controlados por diferentes tipos de señales (bioquímicas, bio-electromagnéticas, biomecánicas) y su interacción entre sí, con la célula y con el medio [1].
La complejidad intrínseca de los mecanismos mencionados y los agentes involucrados, junto con el conocimiento insuficiente de muchos de ellos, impiden su modelamiento computacional completo y por lo tanto la disponibilidad de predicciones confiables sobre los efectos específicos o condiciones de cambio de medio.
Sin embargo, el alcance de los métodos computacionales es hoy en día suficiente para comprobar hipótesis fundamentales, para entender las implicaciones de suposiciones biofísicas, para proporcionar contra ejemplos y para explorar nuevas ideas que son usadas para diseñar nuevos experimentos [1].
La osificación endocondral es uno de los procesos esenciales en biología del desarrollo del hueso y en morfogénesis, con muchas características comunes con otros procesos de cicatrización de los tejidos humanos, con la medicina regenerativa y con la ingeniería de tejidos. La osificación endocondral consiste en el reemplazo del cartílago hialino por hueso. En huesos largos, es iniciada en el denominado centro de osificación primario ubicado en la mitad de la diáfisis. El frente de osificación avanza hacia la epífisis, simultáneamente con el crecimiento longitudinal del hueso. Posteriormente, se desarrollan los centros secundarios de osificación que se forman después de la natalidad dentro de cada condroepífisis [2-7].
Hasta el momento, existen diferentes teorías que han sido propuestas para explicar los progresos de osificación secundaria [3, 6, 8-11]. Algunas de ellas suponen que la hormona paratiroidea (PTHrP) y la proteína Indian Hedgehog (Ihh) son los principales factores responsables para la regulación de la tasa de hipertrofia de condrocitos [3]. PTHrP retarda la hipertrofia mientras que Ihh la promueve. [3,11]. Kronenberg [3], y Provot y Schipani [6] proponen que estos dos factores paracrinos forman un bucle regulatorio, donde Ihh promueve la producción de PTHrP mientras que PTHrP inhibe la secreción de Ihh. Por otra parte, los condrocitos hipertrofiados son las principales células reguladoras en formación ósea por estimular la mineralización en la matriz circundante y por atraer vasos sanguíneos y con ellos los precursores de las células óseas (osteoblastos y osteoclastos) [12-14], este proceso está regulado por diferentes substancias como el factor de crecimiento endotelial vascular (VEGF) [15-18]. Por lo tanto, la hipertrofia de condrocitos es por consiguiente la clave para la formación de los centros secundarios de osificación [4,8].
Siguiendo la suposición que PTHrP e Ihh forman un bucle regulatorio bioquímico [3, 6], en este trabajo se implementa dicho mecanismo regulatorio utilizando un sistema de ecuaciones de reacción-difusión [19, 20] ampliamente usadas en morfogénesis, en las que los factores bioquímicos se suponen secretados por condrocitos proliferativos.
El modelo aquí propuesto es similar a los modelos que usan ecuaciones clásicas de reacción-difusión, pero se diferencia en el hecho que la síntesis de los factores paracrinos es debida a la proliferación y población de condrocitos pre-hipertróficos que existen en la cabeza de la epífisis. Esta suposición implica que los parámetros no son homogéneos en el espacio, complicando el análisis matemático y el correspondiente proceso de solución en comparación con parámetros homogéneos espacialmente [19-21]. No obstante, se obtienen soluciones estables de dichos conjunto de ecuaciones bajo un rango suficientemente amplio de parámetros, condiciones iniciales y de contorno que guían al mismo patrón espacial como se observa en la naturaleza.
Estas características permiten plantear la hipótesis en la cual los patrones (de aparición y localización) de los centros de osificación secundarios pueden ser interpretados, desde un punto de vista matemático, como los patrones espaciales asociados a las características de inestabilidad de Turing, es decir, soluciones estables en el tiempo con un arreglo espacial típico asociado a cada rango de parámetros del modelo [22-24]. Estas soluciones pueden ser identificadas físicamente en nuestro caso con concentraciones locales estables de los agentes químicos de reacción y los condrocitos hipertrofiados que guiarán la aparición inicial de los centros de osificación secundarios.
En adelante, se presenta el modelo computacional utilizado capaz de predecir el origen de los centros de osificación secundarios regulados por las concentraciones espaciales de PTHrP e Ihh, la población de condrocitos y la geometría de la epífisis (tamaño y forma). Se destacan los resultados numéricos obtenidos y se realiza una discusión con referencia a la realidad biológica del crecimiento óseo.
2. MATERIALES Y MÉTODOS
2.1 Descripción del Modelo
El proceso regulatorio que proponemos en este modelo
está esquematizado en la figura 1 [3]. En ella se muestra la relación entre las
señales moleculares y la hipertrofia de
condrocitos. La línea curva significa hipertrofia. La línea discontinua
significa inhibición. La línea continua significa activación. PC representa condrocitos proliferativos, HC quiere decir condrocitos hipertróficos, PTHrP se refiere a la hormona paratiroidea, e Ihh hace referencia al Indian Hedgehog. Se observa el bucle
regulatorio entre Ihh y PTHrP donde Ihh (factor activador) estimula la
producción de PTHrP, mientras que PTHrP (factor inhibidor) inhibe la secreción de Ihh.
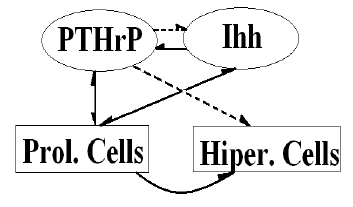
Figura 1. Sistema de control de los procesos
moleculares y celulares [3]
Figure 1. Control system of the molecular and cell
processes [3]
Por consiguiente, se propone que este mecanismo regulatorio sea modelado mediante ecuaciones de reacción-difusión, donde el término de reacción en el proceso bioquímico de reacción-difusión (síntesis de factores paracrinos) depende de la concentración de reactantes y de la densidad de condrocitos proliferativos, mientras que la tasa de hipertrofia depende de la concentración de Ihh. La suposición principal es que los patrones de origen para los centros de osificación secundarios corresponden, desde un punto de vista matemático, al patrón espacial que tiene lugar en la aproximación de Turing cuando dos reactivos interactúan químicamente (ver figura 1) [3].
La definición de las relaciones indicadas en la figura 1 puede ser cuantificada por medio de ecuaciones que establecen el cambio local de factores paracrinos, condrocitos proliferativos y condrocitos hipertrofiados. Estas ecuaciones son:
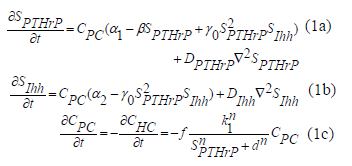
En (1), CPC es la concentración de condrocitos proliferativos, CHC es la de los condrocitos hipertrofiados, y 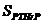 y
y 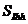 son concentraciones de
PTHrP e Ihh, respectivamente. Los demás son parámetros del modelo. a1 y a2 son términos de origen que cuantifican
la producción de cada factor molecular por la proliferación de células, b1 es una constante que
cuantifica la inhibición de PTHrP por su
propio exceso, g0 regula la interacción no lineal entre PTHrP y las concentraciones
de Ihh que cuantifican la producción o inhibición de cada factor molecular, DPTHrP y DIhh son los coeficientes de difusión de PTHrP e Ihh,
respectivamente.
son concentraciones de
PTHrP e Ihh, respectivamente. Los demás son parámetros del modelo. a1 y a2 son términos de origen que cuantifican
la producción de cada factor molecular por la proliferación de células, b1 es una constante que
cuantifica la inhibición de PTHrP por su
propio exceso, g0 regula la interacción no lineal entre PTHrP y las concentraciones
de Ihh que cuantifican la producción o inhibición de cada factor molecular, DPTHrP y DIhh son los coeficientes de difusión de PTHrP e Ihh,
respectivamente.
La interpretación biológica de las ecuaciones en (1) indica que el término g0SPTHrP2SIhh es la representación de la activación no lineal de SPTHrP (producción de PTHrP bajo la presencia de Ihh). Además, f es la frecuencia de la hipertrofia (porcentaje de condrocitos que hipertrofian por unidad de tiempo), k1 es una constante que también cuantifica la tasa de hipertrofia y finalmente d es el umbral de PTHrP para iniciar hipertrofia.
2.2 Ejemplos de Aplicación
Al revisar el potencial del modelo aquí propuesto para
predecir el origen de los centros secundarios de osificación, se analizaron las
diferentes formas y tamaños de la epífisis de un hueso largo, correspondiente a
diferentes animales y/o órganos. En particular, se utilizaron las geometrías
mostradas en las figura 2a y 2b que corresponden a la epífisis de un fémur de
un mamífero, como pro ejemplo, un el humano. Las dimensiones son
20 mm. de alto y 16 mm. de ancho para la
figura 2a, y 20 mm.
de alto y 22 mm.
De ancho para la figura 2b [25]. Un tercer caso correspondiente al fémur de una rata que fue
analizado con la geometría y tamaño mostrado en la figura 3, cuyas dimensiones
son
5 mm.
de ancho y 5 mm.
de alto.
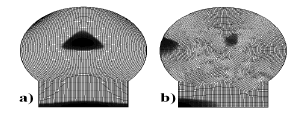
Figura 2. Geometría de la epífisis para grandes
animales. (a) Epífisis normal. (b) otras mallas probadas no estructuradas
Figure 2. Geometry of the bone epyphisis for large
animals. (a) Normal epyphisis, (b) Another meshes proved (unstructured)
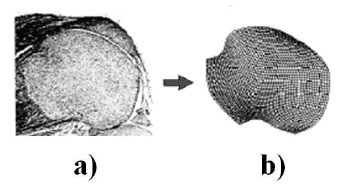
Figura 3. Geometría de la epífisis ósea de animales
pequeños, específicamente una rata. (a) Micrografía. (b)
Modelo en elementos finites
Figure 3. Geometry of the bone epyphisis for small
animals, specifically a rat. (a) Micrography, (b) finite elements model
En todos los casos, la simulación comienza con condiciones iniciales similares (ver figuras 6, 7 y 8 en 0 días): Población uniforme de condrocitos proliferativos en todas las epífisis, una alta concentración del factor molecular inhibidor (PTHrP) en el pericondrio articular (1.5 ngml–1) y una alta concentración del factor molecular activador (Ihh) en el frente de osificación primaria (1.1 ngml–1) (figura 6, día 0).
2.3 Estimación
de Valores de Parámetros
El conjunto de ecuaciones previamente presentadas
corresponde a un sistema acoplado donde las ecuaciones correspondientes a
factores moleculares (PTHrP y Ihh), son ecuaciones de reacción-difusión
extendidas, similares a un sistema de Turing que expone inestabilidad por
reacción-difusión. Para (DPTHrP, DIhh ¹0), la inestabilidad
reacción-difusión (Turing) aparece para una cierta combinación de parámetros
[19,20]. Esto define un dominio en el espacio de parámetros, llamado espacio de Turing [19,20].
Para obtener el espacio de Turing se necesita un
análisis de estabilidad lineal del sistema reacción-difusión alrededor de la
solución homogénea, la cual se obtiene forzando a que la solución sea de la
forma 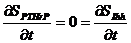 , con lo que se obtiene
, con lo que se obtiene 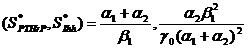 , que
, que
son los puntos de estado estable de la solución de las
ecuaciones (1a) y (1b). El análisis lineal permite encontrar la solución
espacial lineal y los rangos de parámetros que garanticen la aparición de cada
uno de los patrones específicos. Por consiguiente, la solución está expresada
como 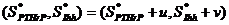 , donde u y v son pequeñas perturbaciones alrededor
del estado estable. A partir de (1a) y
(1b) los resultados de estos análisis lineales permiten escribir las siguientes
inecuaciones (ver [26,27]):
, donde u y v son pequeñas perturbaciones alrededor
del estado estable. A partir de (1a) y
(1b) los resultados de estos análisis lineales permiten escribir las siguientes
inecuaciones (ver [26,27]):
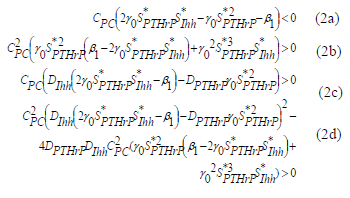
Comparando la forma adimensional de las ecuaciones estándar de Schnakenberg [26,27]:

con las ecuaciones descritas en (1a) y (1b) se pueden identificar los parámetros por comparación de los coeficientes de las ecuaciones de Schnakenberg y las de nuestro modelo, tal que:
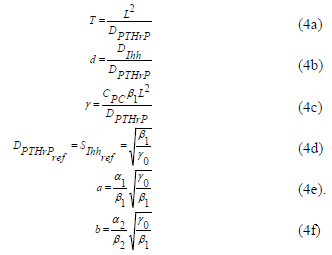
Tabla 1. Modos de vibración para el modelo adimensional
de Schnakenberg con a= 0.1 y b= 0.9, y L
= 1
Table 1. Vibration modes for
the dimensionless Schnakenberg model with a = 0.1 and b = 0.9, and L = 1

Estos seis parámetros caracterizan el modelo de Schnakenberg. Por ejemplo, Madzvarnuse [26] obtuvo valores correspondientes a diferentes números de onda para un rango específico de este conjunto de parámetros en un dominio cuadrado bidimensional unitario 2D (ver tabla 4 y figura 4):

Figura 4. Patrones espaciales para las soluciones de las
ecuaciones de Schankenberg correspondientes a diferentes grupos de parámetros.
Arriba, la solución para un modo de vibración de (4,4) (cuatro semi-ondas) a lo largo de las direcciones asociadas x y
y, con a=0.1, b=0.9, d=8.6076 y g=909.66.
Abajo, la solución para un modo de vibración de (1,2) con a=0.1, b=0.9,
d=9.1676 y g= 176.72
Figure 4. Spatial patterns for the solutions of the Schankenberg
equations corresponding to different sets of parameters. Left, solution for a
vibration mode of (4,4) (four semi-waves along the x and y directions
associated to a = 0.1, b = 0.9, d = 8.6076 and = 909.66. Right, solution for a vibration mode of (1,2) with a = 0.1, b
= 0.9, d = 9.1676 and γ = 176.72
En el caso del este modelo es necesario definir un primer conjunto de ocho parámetros (ver ecuación (4)). Para estimarlos, inicialmente se toman en cuenta algunas evidencias experimentales:
- SPTHrP =1ng/ml [28].
- Periodo promedio para la formación del patrón del centro secundario de osificación en la etapa del desarrollo postnatal T= 1 mes [29].
- Diámetro de cabeza femoral de 16 mm. L = Lx = Ly = 16 mm.
- García-Aznar et al. [30] usaron una concentración máxima de células cartilaginosas de CPC = 105 células / mm3 en el proceso de consolidación en la cicatrización de una fractura.
Se fijan cuatro parámetros, T, SPTHrPref o SIhhref, L y CPC. Entonces, usando (4a) se obtiene DPTHrP = 9.9 (10–11)m2s–1 y, con (4d) b1= g0 (10–8). Por consiguiente, es necesario definir cuatro parámetros adicionales DIhh, b1 (ó g0), a1 y a2 (ver tabla 2).
Tabla 2. Conjunto de valores
para el proceso de osificación endocondral
Table 2. Set of values for the endochondral
ossification process
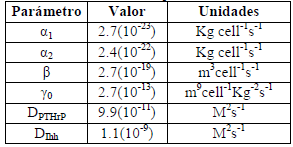
Como el centro secundario de osificación debe aparecer aproximadamente en el centro de la cabeza del hueso, se estima que el numero de onda para este proceso es (1,1), en otras palabras necesitamos representar media onda estable de PTHrP y de Ihh a lo largo de la dirección x e y. Para reproducir este patrón todos los parámetros deben estar en el espacio de Turing y cumplir con las restricciones (2). Existen combinaciones infinitas de DIhh, b1, a1 y a2 (o equivalentemente a, b, g y d de la tabla 1) parámetros que cumplen con las restricciones de Turing y que induce un patrón de (1,1). Como no se tiene certeza de valores experimentales de algunos de estos parámetros, se han fijado para la presente simulación. Como primera aproximación se fija a=0.1 y b=0.9. Así como también se fija el patrón de inestabilidad que debe aparecer (1,1) en este caso, el resto de los parámetros fueron plenamente definidos g=11.5776 y d =70.6 o equivalentemente están definidos los parámetros DIhh, b1, a1 y a2 (ver tabla 3).
Tabla 3. Otros
parámetros de nuestro modelo
Table 3. Other parameters of our model

En conclusión, se encuentran diferentes conjuntos de parámetros con algún patrón, que cumplen con las condiciones de Turing. Se pueden escoger diversos valores de parámetros para obtener diferentes resultados, especialmente:
- Los parámetros cumplen con las restricciones de Turing en (2), pero se pueden tener diferentes números de onda utilizando otros valores de la tabla 1, ó,
- Los parámetros no cumplen con las condiciones de Turing en (2), luego no es posible un patrón espacial estable.
2.4 Implementación
Numérica
Estas ecuaciones han sido implementadas y resueltas numéricamente
dentro del contexto de los Elementos Finitos. La simulación computacional fue hecha
por un procedimiento incremental-iterativo que permite calcular la evolución de
la concentración de los factores paracrinos (SPTHrP, SIhh)
y la población de condrocitos (CPC, CHC). La integración
del tiempo fue desarrollado por medio de un esquema de diferencias hacia atrás
de Euler mientras que el lazo iterativo fue resuelto por una aproximación de
punto fijo.
Se supone que el cartílago hialino inicial es una matriz estructural con una concentración inicial de condrocitos de 105 células / mm3. Las concentraciones iniciales de PTHrP e Ihh fueron respectivamente fijadas en el pericondrio articular y en el centro del cartílago hialino [3]. Esta suposición está inspirada en los modelos biológicos de desarrollo [26] en los cuales las condiciones iniciales son tomadas como perturbaciones pequeñas alrededor de un estado estable uniforme.
3. RESULTADOS
Como consecuencia de la interacción química entre ambos reactantes, se predijo un patrón espacial estable en el tiempo. Las figuras muestran la evolución en el tiempo de la concentración de factores paracrinos y la densidad de los condrocitos hipertrofiados. En la figura 5c, por ejemplo, se observa la evolución de la hipertrofia de condrocitos, aproximadamente a los 1.5 meses, en un área cercana al frente de osificación primaria, específicamente en el centro de la epífisis. Después de 3 meses, se produce un centro secundario de osificación debido a la baja concentración del inhibidor (PTHrP) (figura 5a). Por consiguiente, se observa la concordancia ligada entre la localización del centro secundario de osificación en un mamífero (un cerdo), mostrado en la figura 5d [35], y nuestra predicción numérica. Por su parte, en la figura 6 se muestra la evolución del nivel de hipertrofia de los condorcitos que conforman el centro secundario de osificación en hueso cuya cabeza es más grande, como ocurre, por ejemplo en el fémur en la articulación de la rodilla. Aquí se nota la aparición de dos centros secundarios de osificación, similar a lo que ocurre en la realidad clínica.
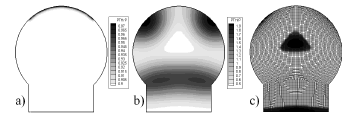
Figura
5. Resultados de la primera geometría simulada, se muestra la formación del centro
de osificación secundaria en un hueso largo un cerdo c). El tiempo de análisis
es postnatal. a) Concentración de PTHrP en el momento del nacimiento; b)
Concentración de PTHrP en t=3.5 meses.; c) Concentración de células
hipertrofiadas
Figure 5. Results for the first simulated geometry,
showing the formation of the secondary ossification centre in a long bone of a
mammal c). Time of analysis is postnatal. a) PTHrP concentration in t=0; b)
PTHrP concentration at t=3.5 months

Figura
6. Resultados para la segunda geometría simulada, se muestra la formación de los
centros de osificación secundaria en un hueso largo de un mamífero con una
cabeza ancha. El tiempo de análisis es postnatal. a) Concentración de PTHrP; b)
concentración de Ihh; c) concentración de células hipertrofiadas (en t= 3.5
meses)
Figure 6. Results for the second simulated geometry,
showing the formation of secondary ossification centers in a long bone of a
mammal with a wider head. Time of analysis is postnatal. a) PTHrP
concentration; b) Ihh concentration; c) Concentration of hypertrophied cells (at t= 3.5 months).
A continuación, se analiza el caso de un hueso largo de un animal pequeño, como una rata (Fig. 7). En este caso, el espacio disponible para que los factores paracrinos interactúen es mucho menor debido a las dimensiones de la cabeza del hueso, generando, sorprendentemente, un patrón completamente diferente con la localización de áreas específicas en la periferia de la epífisis. Este hecho, podría en realidad corresponder al desarrollo de los canales del cartílago que han sido observados experimentalmente en esta clase de animales, en lugares cerca de los contornos de la epífisis (ver fig. 7 y su contraste experimental figura 8).

Figura
7. Formación de los centros secundarios de osificación en un animal pequeño como
una rata. La osificación comienza en dos lugares cerca del contorno. El tiempo
de análisis es postnatal. a) Concentración de PTHrP; b) Concentración de Ihh;
c) Concentración de células hipertrofiadas (en t=11 días)
Figure 7. Formation of secondary ossification centers in
a small animal like a rat. Ossification starts at two places near the boundary.
Time of analysis is postnatal. a) PTHrP concentration; b) Ihh concentration; c)
Concentration of hypertrophied cells (at t=11 days)

Figura
8. Brote de invasión vascular en el cóndilo de la periferia femoral de un ratón
Figure 8. Vascular bud invasion
in the peripherical femoral condyle of a mouse
4. DISCUSIÓN
Aunque la aplicación de los modelos de Turing en biología del desarrollo han sido continuamente sujeto de controversia [36,24], ha aparecido un interés reciente como consecuencia del trabajo presentado por Sick et. al [37] en el cual confirma la validación de las ecuaciones de reacción-difusión en un ejemplo específico de formación de patrones biológicos (crecimiento del folículo de cabello). El trabajo aquí presentado ilustra y sustenta la validación de estos modelos para describir los procesos fundamentales que ocurren durante los eventos complejos de formación de patrones en la biología del hueso. De los resultados mostrados hasta este punto, se concluye que la retroalimentación química entre dos factores moleculares reactivos (activador-inhibidor) en la epífisis de los huesos largos puede ser una razón importante para haber encontrado un patrón espacial estable complejo en el origen de los centros secundarios de osificación, y puede también ayudar a explicar la dependencia de cada patrón en el tamaño y la forma de la cabeza del hueso, en concordancia con lo que ha sido experimentalmente observado en diferentes animales.
No obstante, estos resultados han sido obtenidos con un modelo matemático basado en suposiciones y simplificaciones que tienen que ser señalados y discutidos.
Se presenta la hipótesis que el origen de los centros secundarios de osificación están regulados por células a través de dos reactantes bioquímicos (se han asumido Ihh-PTHrP). No obstante, se conoce que en esa etapa de desarrollo del hueso existen otros factores moleculares actuando en la epífisis (Ej. BMP, TGF-β, FGFs, etc.) [17]. Hasta ahora, se presenta un gran esfuerzo en este trabajo por aclarar la misión de cada una de estas sustancias, su interacción completa y la regulación de sus procesos. Esta misión es posible por la existencia de un mecanismo activador-inhibidor que garantiza una alta estabilidad para este proceso de desarrollo. En el modelo se suponen, como condiciones iniciales, que el factor inhibidor es generado por células pericondriales en la parte superior de la epífisis, mientras que el factor activador es producido en la parte baja, en el centro de osificación primaria. Sin embargo, el tipo de inestabilidad espacial obtenida es casi independiente de las condiciones iniciales. De hecho, el modelo conduce al mismo estado final estable (estado atractor), incluso si comenzamos desde casi cualquier condición inicial con parámetros similares a los usados en este trabajo. Este modelo es por tanto muy estable y robusto en consideración a las condiciones iniciales y a un rango de parámetros
La producción de factores activador-inhibidor se debe a los condrocitos proliferativos, aunque los condrocitos pre-hipertrofiados pueden también secretar estos y otros factores, estos condrocitos principalmente aparecen una vez se desarrolla el centro secundario de osificación. Sin embargo, se hace especial enfoque sólo a la aparición de los centros secundarios de osificación, y no en su desarrollo completo durante la formación del hueso. Para esta etapa subsiguiente, un modelo que sólo incorpore influencias químicas probablemente no será suficiente, también se debe tomar en cuenta las restricciones de carga y contorno (efectos mecánicos) y factores bioquímicos adicionales.
El valor numérico de algunos de los parámetros usados en la simulación es desconocido, y por lo tanto, han sido supuestos. De hecho, tenemos sólo valores encontrados en la literatura sobre experimentos similares. Por ejemplo, Liang et. Al. [31] ha experimentado con BSA (Bovine Serum Albumin) in hidrogel en 37 grados Celsius donde encontraron un coeficiente de difusión en el rango 4.98-8.21 (10–11) m2/s. Philipott et al [32] midió la difusión de las hormonas LH en células de rata encontrando un coeficiente de difusión de 5.8 (10–14) m2/s. En nuestro análisis los valores estimados resultaron en un rango similar a los encontrados.
Para concluir, a pesar de todas las simplificaciones y limitaciones antes mencionadas, el modelo matemático propuesto es capaz de reproducir muchas de las características del origen de los centros secundarios de osificación, incluyendo su insensibilidad relativa a las condiciones iniciales y valores de los parámetros, y su dependencia sobre la forma y tamaño de la cabeza de la epífisis, o, equivalentemente, en la etapa del desarrollo de la cabeza ósea. En adición, esta aproximación permite nuevas ideas a pruebas experimentales para demostrar no sólo la validez de las suposiciones fundamentales citadas anteriormente sino también que los parámetros en las ecuaciones de control satisfacen las restricciones del modelo.
5. AGRADECIMIENTOS
D.A. Garzón-Alvarado fue financiado por la DIB (División de Investigación de Bogotá, Universidad Nacional de Colombia) mediante el apoyo al proyecto "Modelado Matemático y Simulación de Procesos en Ingeniería Mecánica y Biomédica: Segunda Fase". Código DIB 8008170.
REFERENCIAS
[1] VAN DER MEULEN, M.C y HUIKES, R. Why Mechanobiology? J.Biomech., 35(4): 401-414, 2002.
[2] FRANCESCHINI, M.P. On the appearance and evolution of secondary centers of ossification in the tibia of Gallus gallus. Acta Anat., 68:169-188, 1967.
[3] KRONENBERG, H.M. Development regulation of the growth plate. Nature, 423:332-336, 2003.
[4] MORINI, S., CONTINENZA, M., RICCIARDI, A.G., GAUDIO, E y PANNARALE, L. Development of the microcirculation of the secondary ossification center in rat humeral head. Anat. Rec. Part A., 278A:419-427, 2004.
[5] DE CROMBRUGGHE, B., LEFEBVRE, V y NAKASHIMA, K. Regulatory mechanisms in the pathways of cartilage and bone formation. Curr. Opin. Cell. Biol., 13(6):721-728, 2001.
[6] PROVOT, S y SCHIPANI, E. Molecular mechanisms of endochondral bone development. Biochem. Bioh. Res. Co., 328(3):658-665, 2005.
[7] KARP, S., SCHIPANI, E., ST-JACQUES, B., HUNZELMAN, J., KRONENBERG, H y MCMAHON, A.P. Indian Hedgehog coordinates endochondral bone growth and morphogenesis via Parathyroid Hormone related-Protein -dependent and -independent pathways. Development, 127:543-548, 2000.
[8] SUNDARAMURTHY, S y MAO, J. Modulation of endochondral development of the distal femoral condyle by mechanical loading. J. Orthop. Res., 24:229-241, 2006.
[9] CARTER, D.R y WONG, M.A theoretical model of endochondral ossification and bone architectural construction in long bone ontogeny. Anat. Embryol.
[10] HENDERSON, J y CARTER, D.R.. Mechanical induction in limb morphogenesis: The role of growth-generated strains and pressures. Bone, 31(6):645-653, 2002.
[11] KOBAYASHI, T., SOEGIARTO, D.W., YANG, Y., LANSKE, B., SCHIPANI, E., MCMAHON, A.P y KRONENBERG, H. M. Indian Hedgehog stimulates periarticular chondrocyte differentiation to regulate growth plate length independently of PTHrP. J. Clin. Invest., 115:1734-1742, 2005.
[12] CHUNG, U., SCHIPANI, E., MCMAHON, A.P y KRONENBERG, H.M. Indian Hedgehog couples chondrogenesis to osteogenesis in endochondral bone development. J. Clin. Invest., 107(3):295-304, 2001.
[13] KINDBLOM, J.M., NILSSON, O., HURME, T., OHLSSON, C y SAVENDAH, J.L. Expression and localization of Indian Hedgehog (Ihh) and Parathyroid hormone related protein (PTHrP) in the human growth plate during pubertal development. J. Endocrinol., 174:R1-R6, 2002.
[14] KOBAYASHI, T., CHUNG, U.I., SCHIPANI, E., STARBUCK, M., KARSENTY, G., KATAGIRI, T., GOAD, D.L., LANSKE, B y KRONENBERG H.M. PTHrP and Indian Hedgehog control differentiation of growth plate chondrocytes at multiple steps. Development, 129:2977-2986, 2002.
[15] ZELZER, E., MAMLUK, R., FERRARA, N., JOHNSON, R., SCHIPANI, E y OLSEN, B. VEGFA is necessary for chondrocytes survival during bone development. Development, 131:2161- 2171, 2003.
[16] ST-JACQUES, B., HAMMERSCHMIDT, M., y MCMAHON, A. Indian Hedgehog signaling regulates proliferation and differentiation of chondrocytes and is essential for bone formation. Gene Dev., 13:2072-2086, 1999.
[17] FISHER, M.C., MEYER, C., GARBER, G y DEALY, C. Role of IGFBP2, IGF-I and IGF-II in regulating long bone growth. Bone, 37(6):741-750, 2005.
[18] VORTKAMP, A., LEE, K., LANSKE, B., SEGRE, G.V., KRONENBERG, H.M y TABIN, C.J. Regulation of rate of cartilage differentiation by Indian hedgehog and PTH- related protein. Science, 273:613-622, 1996.
[19] MADZVAMUSE, A., MAINI, P.K y WATHEN, A.J. A moving grid finite element method for the simulation of pattern generation by Turing models on growing domains. J. Sci. Comput., 24:247-262, 2005.
[20] CRAMPIN, E. J y MAINI, P. K. Reaction-diffusion models for biological pattern formation. Methods and Applications of Analysis, 8(3):415-428, 2001.
[21] PAGE, K.M., MAINI, P.K., y MONK, N.A.M. Complex pattern formation in reaction-diffusion systems with spatially varying parameters. Physica D: Nonlinear Phenomena, 202(1-2):95-115, 2005.
[22] MURRAY, J.D y MAINI, P. K. A new approach to the generation of pattern and form in embriology. Sci. Prog., 70:539-553, 1986.
[23] MAINI, P. K., BAKER, R.E., y CHUONG, C.M. The Turing model comes of molecular age. Science, 314:1397-1398, 2006.
[24] MAINI, P.K y MURRAY, J.D. A nonlinear analysis of a mechanical model for pattern formation. SIAM. J. Appl. Math., 48:1064-1072, 1998.
[25] SHEFELBINE, S.J., TARDIEU, C., y CARTER, D.R. Development of the femoral bicondylar angle in hominid bipedalism. Bone, 30(5):765-770, 2002.
[26] MADZVAMUSE, A. A numerical approach to the study of spatial pattern formation. Oxford University, U.K. , Ph.D. Thesis, 2000.
[27] MADZVAMUSE, A. Time-stepping schemes for moving grid finite elements applied to reaction-diffusion systems on fixed and growing domains. Journal of Computational Physics, 214:239-263, 2006.
[28] LI, T., DONG, Y., IONESCU, A., ROSIER, R., ZUSCIK, M., SCWARZ, E., O'KEEFE, R., y DRISSI, H. Parathyroid hormone-related peptide (PTHrP) inhibits RUNX2 expression through the PKA signaling pathway. Experimental Cell Research, 299(1):128-136, 2004.
[29] ZYLAN, T y MURSHID, K.W. An assesment of femur growth parameters in human fetuses and their relationship to gestional age. Turk J Med Sci, 33:27-32, 2003.
[30] GARCÍA-AZNAR, J.M., KUIPER, J.H., GÓMEZ-BENITO, M.J., DOBLARÉ, M y RICHARDSON, J.B. Computational simulation of fracture healing: Influence of interfragmentary movement on the callus growth. Journal of Biomechanics, 40(7):1467-76, 2007.
[31] LIANG, S., XU, J., WENG, L., DAI, H., ZHANG, X y. ZHANG, L. Protein diffusion in agorase hydrogel in situ measured by improved refractiveindex method. Journal of Controlled Release, 115, 2006.
[32] PHILPOTT, C., RAHMAN, N., KENNY, N., UNDO, T., YOUNG, R., BARISAS, G y ROESS, D. Rotational dynamics of leutinizing hormone receptors and MHC class I antigens on murine Leydig Cells. Biochimica et Biophysics Acta, 1235, 1995.
[33] FARNUM, C.E., LEE, R., OHARA, K y URBAN, J.P.G. Volume increase in growth plate chondrocytes during hypertrophy: the contribution of organic osmolytes. Bone, 30(4):574-581, 2002.
[34] FORRIOL, F y SHAPIRO, F. Bone Development. Clinical Orthopaedics and Related Research, 432, 2005.
[35] CONNOLLY, S.A. , JARAMILLO, D., HONG, J.K y SHAPIRO, F. Skeletal development in fetal pig specimens: M. R. imaging of femur with Histologic comparison. Radiology, 233:505-514, 2004.
[36] SICK, S., REINKER, S., TIMMER, J., y SCHLAKE, T. WNT and DKK determine hair follicle spacing through a reaction-diffusion mechanism. Science, 314:1447-1450, 2006.
[37] CARTER, D. R y WONG, M. The role of mechanical loading histories in the development of diarthrodial joints. J. Orthop. Res., 6:804-816, 1988.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2009 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.

















