FIBRA MICRO-ESTRUCTURADA PARA LA COMPENSACIÓN DE LA DISPERSIÓN CROMÁTICA EN SISTEMAS DE COMUNICACIONES ÓPTICAS
Palabras clave:
Modelación numérica de fibras ópticas, Diseño y fabricación de fibras, Fibras ópticas, Fibras de cristal fotónico, Fibras micro-estructuradas, Dispersión en fibras ópticas. (es)FIBRA MICRO-ESTRUCTURADA PARA LA COMPENSACIÓN DE LA DISPERSIÓN CROMÁTICA EN SISTEMAS DE COMUNICACIONES ÓPTICAS
MICRO-STRUCTURED FIBER FOR CHROMATIC DISPERSION COMPENSATION IN OPTIC COMMUNICATION SYSTEMS
VICTOR H. ARISTIZABAL
Escuela de Física, Universidad
Nacional de Colombia – Medellín, vharisti@unal.edu.co
Recibido para revisar agosto 29 de 2008, aceptado julio 17 de 2009, versión final agosto 10 de 2009
RESUMEN: En este trabajo se analiza una fibra óptica micro-estructurada que presenta un pico de dispersión anómala aproximadamente de -5800 ps/(nm-km) alrededor 1.547 mm, haciéndola ideal para propósitos de compensación en la tercera ventana de los sistemas ópticos de comunicaciones. Esta fibra especial consiste en un medio homogéneo de Sílice de alta pureza con huecos de aire de diámetros diferentes, dispuestos en siete anillos hexagonales que se mantienen a lo largo de la estructura. Para el análisis se utilizó el método de los elementos finitos debido a que exhibe una estructura compleja donde el tratamiento analítico no es posible.
PALABRAS CLAVE: Modelación numérica de fibras ópticas, Diseño y fabricación de fibras, Fibras ópticas, Fibras de cristal fotónico, Fibras micro-estructuradas, Dispersión en fibras ópticas.
ABSTRACT: In this work, a micro-structured fiber features a peak of anomalous dispersion about -5800 ps/(nm-km) around 1.547 mm is analyzed. It is ideal for compensation purposes in the third window of the optical communications. This special fiber consisting of a homogeneous Silica region with different diameter air-holes, they are arranged at seven hexagonal rings that run along the length of the structure. For the analysis the finite elements method was utilized due to it exhibit a complex structure where analytic treatment is impossible.
KEYWORDS: Optical fibers numeric modeling, Fiber design and fabrication, Fiber optics, Photonic crystal fibers, Micro-structured fibers, Dispersion in fiber optics.
1. INTRODUCCIÓN
La dispersión en un sistema de comunicaciones surge cuando el tiempo de duración de un pulso de luz se extiende durante la transmisión en una fibra óptica. Un pulso corto de luz, al experimentar lo anterior, se hace más largo traslapándose con los pulso adyacentes, dando como resultado un flujo de bits poco confiable, tal como se muestra en la Figura 1 donde los círculos en las figuras representa embobinados de fibra óptica. Las figuras (a) y (b) muestran la dependencia de la distorsión de la señal con la distancia, es decir, la señal experimenta mayor dispersión a distancias más largas, al punto tal que no se puede resolver los bits enviados dando como resultado final una limitación en la velocidad de transmisión en el sistema óptico de comunicaciones.
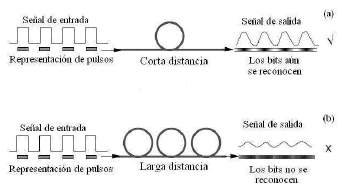
Figura 1. Efecto de la dispersión con la distancia en
la señal que viaja en la fibra
Figure
1. Dispersion effect as distance function of the signal
that travels into the fiber
Hay varias clases de dispersión, las más significativas son la dispersión cromática, dispersión modal y dispersión de guía de onda (hay una amplia descripción de cada una de ellas en [1]).Cada una es generada por mecanismos diferentes pero al final producen el mismo efecto sobre el pulso que se propaga.
Los más recientes avances en tecnología de fibra óptica se han interesado en el desarrollo de dispositivos ópticos alrededor de 1.55 mm (tercera ventana de telecomunicaciones) para la transmisión de información sobre enlaces ópticos instalados años atrás a 0.850 mm y 1.3 mm (primera y segunda ventana de telecomunicaciones, respectivamente). No obstante, estos sistemas presentan dispersión cromática positiva (o normal), lo cual limita la velocidad de transmisión de datos. Esta dispersión normal puede ser compensada mediante la introducción de dispositivos relativamente pequeños con altos valores de dispersión de signo opuesto, es decir, dispersión negativa (o anómala), y de esta manera se recuperaría la forma del pulso que se introduce al inicio del sistema de transmisión (ver Figura 2).
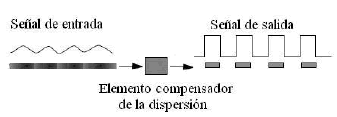
Figura 2. Función del elemento compensador de la
dispersión
Figure
2. Dispersion compensator element function
Muchos dispositivos para la compensación de la dispersión han sido presentados en los últimos años, pero el diseño más eficaz para este fin, basado en fibras convencionales, es la fibra con perfil de índice en forma de W [2]. El diseño básico de una fibra W consiste en dos regiones de núcleo concéntricos separados espacialmente y asimétricamente mediante un juego de regiones de revestimiento [2-10]. Para este tipo de fibra convencional tipo W, el mejor resultado experimental alcanzado para la dispersión es de aproximadamente -1800 ps/(nm-km) [6].
Desde la introducción de las fibras micro-estructuradas, también llamadas fibras de cristal fotónico [11, 12], se han realizado diferentes estructuras que guían señales ópticas utilizando arreglos de huecos micro-estructurados [13]. En estos sistemas, el índice de refracción efectivo de los modos propagantes es un parámetro esencial, pues determina entre otras, las propiedades de dispersión de la guía de ondas.
La gran variedad de posibles formas y arreglos para los huecos demandan el uso de métodos numéricos que permitan modelar adecuadamente la sección transversal de estas estructuras para analizarlas. Adicionalmente, la existencia de interfases con alto contraste en el índice de refracción entre el material con que se fabrican (generalmente Sílice puro) y los huecos de aire, hace necesario considerar una solución vectorial para tomar en cuenta los efectos de polarización del campo óptico. Entre las técnicas propuestas, el método de elementos finitos (FEM: Finite Element Method), se ha utilizado exitosamente, debido a que puede modelar cualquier geometría y heterogeneidad que tenga la guía de ondas. Además, se han desarrollado diferentes formulaciones vectoriales; dentro de estas aproximaciones, existen las que se formulan en término de todas las componentes del campo eléctrico (o magnético) en donde se debe introducir una función de penalidad con coeficientes artificiales para eliminar las soluciones espurias que aparecen mezcladas con las soluciones físicamente aceptables [14], es decir, en estos esquemas la exactitud de la solución depende de dicha penalidad. Este problema fue resuelto con elementos de borde de orden superior [15, 16], haciendo posible la solución de la ecuación de onda vectorial a costa del aumento de la complejidad del algoritmo y, por ende, demandando altos requerimientos computacionales y mayor tiempo de procesamiento.
Como una alternativa más eficiente a las soluciones vectoriales, el autor propuso mejorar la aproximación escalar para ampliar su rango de validez a longitudes de onda largas y fracciones de llenado de aire grandes en fibras de cristal fotónico [17, 18], incluyendo en el análisis por el método de elementos finitos escalar (SFEM), un término de corrección que da cuenta de los efectos de polarización generados por las interfases material-hueco. Para este propósito se usaron elementos triangulares de primer orden, cuya región que delimitan es de índice de refracción homogéneo, y se aprovecha el hecho de que el SFEM provee directamente la distribución del campo sobre la sección transversal de la fibra para la corrección al análisis escalar. Con esta metodología se analizaron exitosamente fibras mono-modo con huecos de geometría circular, distribuidos regularmente sobre la sección transversal.
En este trabajo se quiere aplicar el método para analizar una fibra micro-estructurada con huecos circulares donde su perfil de índice es en forma de W. Por considerarlo de interés, primero se presenta una descripción del método y luego se muestran los resultados obtenidos para el índice efectivo y el parámetro de dispersión de esta estructura reportada en [19].
2. GEOMETRÍA DE LA FIBRA MICRO-ESTRUCTURADA
La fibra micro-estructurada consta de un medio homogéneo de Sílice de alta pureza con un arreglo hexagonal de huecos de aire, de diámetros d diferentes y distancia L entre huecos consecutivos, dispuestos en siete anillos hexagonales que se mantienen a lo largo de la estructura, ver Figuras 3.

Figura 3. Un cuarto de la fibra con los diámetros de
los huecos de aire, donde los números representan los diferentes diámetros
Figure
3. One quarter of the fiber with the air-holes
diameters, where the numbers represent the different diameters
La Figura 4 muestra la estructura junto a su perfil de índice de refracción, donde se puede identificar claramente dos regiones de mayor valor del índice de refracción que actuarían como núcleos, y las demás que son menor harían de revestimiento. Nótese que el primer anillo de huecos se ha desaparecido para así obtener una región central de 4L de diámetro que actúa como núcleo.
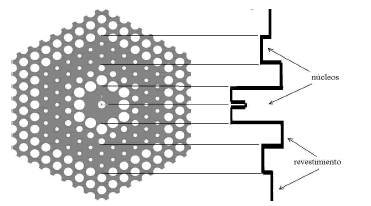
Figura 4. La estructura completa con su perfil de
índice de refracción
Figure
4. Complete structure joins at its refraction index
profile
3. DESCRIPCIÓN DEL MÉTODO DE ANÁLISIS [18]
3.1 Método de Elementos Finitos Escalar
El campo eléctrico
de un modo de propagación en una guía de onda arbitraria se puede expresar como
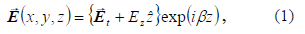
donde b es la constante de
propagación, 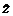 es el vector unitario
paralelo al eje de la guía,
es el vector unitario
paralelo al eje de la guía, 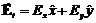 y
y  son las componentes
transversal y longitudinal del campo
eléctrico, respectivamente. Si trabajamos el campo como se describe en (1) en
la ecuación de onda vectorial, fácilmente se puede demostrar que la componente
transversal del campo eléctrico satisface la ecuación de onda:
son las componentes
transversal y longitudinal del campo
eléctrico, respectivamente. Si trabajamos el campo como se describe en (1) en
la ecuación de onda vectorial, fácilmente se puede demostrar que la componente
transversal del campo eléctrico satisface la ecuación de onda:
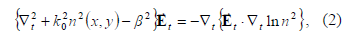
donde 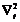 es el operador
Laplaciano en el plano transverso,
es el operador
Laplaciano en el plano transverso,  es el perfil del
índice refracción, y
es el perfil del
índice refracción, y 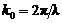 el número de onda en
el vacío, siendo l la longitud de onda.
el número de onda en
el vacío, siendo l la longitud de onda.
La aproximación escalar consiste en despreciar los efectos de acoplamiento de las componentes del campo, haciéndose cero el término a la derecha de la ecuación (2), quedando:
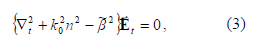
donde 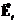 y
y 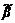 son el campo escalar y
su correspondiente constante de propagación, respectivamente.
son el campo escalar y
su correspondiente constante de propagación, respectivamente.
Para solucionar la ecuación (3) se usa el método de elementos finitos, que convierte la ecuación (3) en el problema matricial de valores propios generalizado:
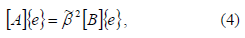
donde el autovector 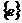 contiene los valores
del campo eléctrico en cada uno de los vértices de los elementos triangulares
utilizado en la discretización de la sección transversal de la guía de onda.
Las matrices
contiene los valores
del campo eléctrico en cada uno de los vértices de los elementos triangulares
utilizado en la discretización de la sección transversal de la guía de onda.
Las matrices 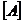 y
y 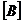 son de la forma:
son de la forma:
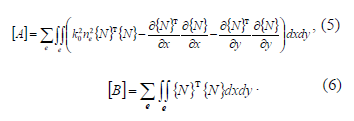
La sumas en (5) y (6) corren sobre todos los
elementos denotados por 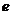 . El índice de refracción
. El índice de refracción  para cada elemento se
considera uniforme e igual a
para cada elemento se
considera uniforme e igual a 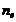 ,
, 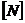 es el vector de
funciones de forma.
es el vector de
funciones de forma.
3.2 Corrección por Polarización
La corrección por polarización a la constante de
propagación proviene, como se concluye de la ecuación (2), de la discontinuidad
del índice de refracción. Para esta corrección se define la relación entre la
constante de propagación  de la ecuación de onda
vectorial (2) y
de la ecuación de onda
vectorial (2) y 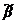 de la ecuación de onda
escalar (3). Para modos polarizados en x o y, la corrección de primer orden
está dada por [20]
de la ecuación de onda
escalar (3). Para modos polarizados en x o y, la corrección de primer orden
está dada por [20]
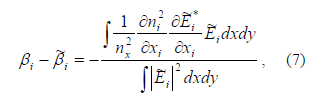
donde i y xi son igual a x o y para modos polarizados en x o y, respectivamente.
El parámetro de dispersión D de una guía de onda se puede calcular a partir de 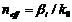 en función de la
longitud de onda a través de la siguiente expresión:
en función de la
longitud de onda a través de la siguiente expresión:
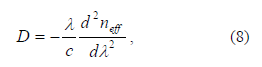
donde c es la velocidad de la luz en el vacío.
Para incluir el efecto de la dispersión cromática del material en la ecuación (8), se utilizó la ecuación de Sellmeier con los coeficientes reportados en la literatura para el Sílice puro [1].
4. RESULTADOS
Para el análisis numérico solo se tomó un cuarto de la estructura debido a la doble simetría que presenta la fibra, tal como se muestra en la Figura 5(a), usando elementos triangulares de primer orden. El discretizado fue refinado en la región que contiene los dos núcleos, porque allí es donde se confina fuertemente el campo eléctrico (Figura 5b).
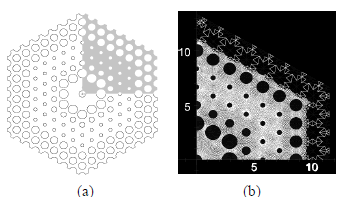
Figura 5. Discretización de un cuarto de la sección
transversal de la fibra
Figure
5. One quarter discretization of the fiber cross section
En las Figuras 6 y 7 se comparan los resultados obtenidos del índice efectivo y el parámetro de dispersión del modo fundamental tipo HE11 con el análisis escalar reportado en [19], sobre un rango de longitud de onda desde 1.530 mm a 1.575 mm. La curva sólida representa el análisis escalar de la Ref. 19, la curva segmentada es nuestro análisis escalar y la curva punteada es nuestro análisis teniendo en cuenta la corrección por efectos de polarización.
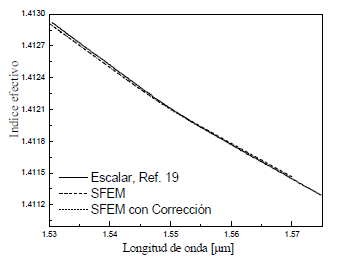
Figura 6. Curva del índice efectivo en función de
la longitud de onda
Figure
6. Effective index curve as wavelength function

Figura 7. Curva del parámetro de dispersión en función
de
la longitud de
onda
Figure
7. Dispersion parameter curve as wavelength function
Nótese que en esta estructura, la luz se propaga en la parte central y en la región que tiene los huecos de aire más pequeños (ver Figura 8), por lo que el acople entre las componentes ortogonales del campo eléctrico es relativamente fuerte y, por consiguiente, el resultado de las soluciones escalares para el índice efectivo y la dispersión difieren de la solución que incluye la corrección por efectos de polarización como se muestra en las figuras 6 y 7.

Figura 8. Perfil de intensidad del campo eléctrico
para el modo tipo HE11 calculado con SFEM
para las longitudes de onda: (a) l=1.530 mm, (b) l=1.547 mm, (c) l=1.570 mm
Figure
8. Electric field intensity profile for HE11-like mode is computed with SFEM to
wavelengths: (a) l=1.530 mm, (b) l=1.547 mm, (c) l=1.570 mm
El análisis muestra que para longitudes de onda inferiores a 1.547 mm la luz está mayoritariamente confinada en el núcleo central y la dispersión es muy pequeña (ver Figuras 7 y 8a), mientras que para longitudes de onda superiores la luz se encuentra mayoritariamente confinada en el núcleo externo y la dispersión también es pequeña (ver Figuras 7 y 8c). En cambio, justo en la longitud de onda de 1.547 mm el índice efectivo cambia drásticamente su pendiente (ver Figura 6) y, por ende, se produce un gran pico de dispersión anómala de aproximadamente -5800 ps/(nm-km) y allí la luz esta confinada en ambos núcleos con igual intensidad (ver Figuras 7 y 8b). Debido a este pico de dispersión anómala es que esta fibra tiene un gran potencial como compensadora de dispersión normal.
5. CONCLUSIONES
En este trabajo se ha aplicado una metodología, basada en el método de elementos finitos escalar que incluye una corrección a la constante de propagación que da cuenta de los efectos de polarización, para analizar guías de onda ópticas micro-estructuradas; de esta manera se acerca más al carácter vectorial del campo electromagnético y, por consiguiente, se obtienen resultados más confiables.
Esta aproximación se ha utilizado para explorar las propiedades de propagación en guías de ondas especiales; en particular, se ha explorado un posible diseño de una guía de onda ideal para aplicaciones de compensación de la dispersión en telecomunicaciones, donde los resultados obtenidos para el índice efectivo y el parámetro de dispersión de la fibra óptica micro-estructurada, que consiste de siete anillos hexagonales de huecos de aire generándose dos regiones de núcleo, muestran que esta disposición particular de los huecos producen un gran pico de dispersión anómala.
6. AGRADECIMIENTOS
Al Dr. Pedro Ignacio Torres Trujillo por su acompañamiento en este trabajo y a la Universidad Nacional de Colombia por su apoyo a través del programa de Becas Nacionales para estudiantes sobresalientes de posgrado.
REFERENCIAS
[1] AGRAWAL, G. P. Fiber-Optic communication Systems, 3rd ed., Section 2.3: Dispersión in single-mode fibers, Wiley-interscience, New York, 2002.
[2] LI, M. J. Recent Progress in fiber dispersion compensators, Procceding 27th Eur. Conf. On Opt. Comm., ECOC'Ol, Amsterdam, 486-489, 2001.
[3] THYAGARAJAN, K., VARSHNEY, R. K., PALAI, P., GHATAK, A. K., GOYAL, I.C. A Novel Design of a Dispersion Compensating Fiber, IEEE Photonics Technology Letters, 8, 1510-1512, 1996.
[4] AKASAKA, Y., SUGIZAKI, R., KOKURA, K. Dispersion Compensating Optical Fiber, United States patent, No. US 5, 673, 354, Sep. 30, 1997.
[5] AUGUSTE, J. L., BLONDY, J. M., CLAPEAU, M., MARCOU, J., DUSSARDIER, B., MONNOM, G., JINDAL, R. Design of a High Negative Chromatic Dispersion in a Single Mode Optical Fibre: Effect of the Central Index Dip, Optics Communications, 178, 71-77, 2000.
[6] AUGUSTE, J. L., JINDAL, R., BLONDY, J. M., CLAPEAU, M., MARCOU, J., DUSSARDIER, B., MONNOM, G., OSTROWSKY, D. B., PAL, B. P., THYAGARAJAN, K. -1800 ps/(nm.km) Chromatic Dispersion at 1.55 mm in Dual Concentric Core Fibre, Electronics Letters, 36, 1689-1691, 2000.
[7] NIELSEN, L .G., KNUDSEN, S. N., EDVOLD, B., VENG, T., MAGNUSSEN, D., LARSEN C. C., DAMSGAAR, H. Dispersion Compensating Fibers, Optical Fiber Technology, 6, 164-180, 2000.
[8] YANDONG, G., SHUISHENG, J. Research on Three-Cladding Dispersion Compensating Fiber with Negative Dispersion Slope, Chinese Journal of Electronics, 9, 48-50, 2000.
[9] AUGUSTE, J. L., BLONDY, J. M., MAURY, J., MARCOU, J., DUSSARDIER, B., MONNOM, G., JINDAL, R., THYAGARAJAN, K., PAL, B.P. Conception, Realization, and Characterization of a Very High Negative Chromatic Dispersion Fiber, Optical Fiber Technology, 8, 89-105, 2002.
[10] GOYAL, I. C., GHATAK, A. K., VARSHNEY, R. K. Dispersion Compensating Fibers, ICTON 2002, 20-23, section A5, 2002.
[11] KNIGHT, J. C., BIRKS, T. A., RUSSELL, P. S. J., ATKIN, D. M. All-silica single-mode optical fiber with photonic crystal cladding, Optics Letters, 21, 1547-1549, 1996.
[12] ARISTIZABAL, V. H. Introducción a la tecnología de fibras ópticas y análisis numérico de la propagación de la luz en fibras ópticas micro-estructuradas, Tecno-Lógicas, 19, 141-165, 2007.
[13] RUSSELL, P. Photonic Crystal Fibers, Science, 299, 358-362, 2003.
[14] RAHMAN, B. M. A., DAVIES, J. B. Penalty function improvement of waveguide solution by finite elements, IEEE Trans. Microwave Theory Technology, MTT-32, 922-929, 1984.
[15] KOSHIBA, M., MARUYAMA, S., HIRAYAMA, K. A vector finite element method with the high-order mixed-interpolating-type triangular elements for optical waveguides problems, Journal Lightwave Technology, 12, 1547-1549, 1996.
[16] KOSHIBA, M., TSUJI, Y. Curvilinear hybrid edge/nodal elements with triangular shape for guided-wave problems, Journal Lightwave Technology, 18, 737-743, 2000.
[17] ARISTIZABAL, V. H., VELEZ, F. J., TORRES, P. I. Modelling of photonic crystalfibers with the scalar finite element method, Procceding SPIE, 5622, 849-854, 2004.
[18] ARISTIZABAL, V. H., VELEZ, F. J., TORRES, P. I. Analysis of photonic crystal fibers: Scalar solution and polarization correction, Optics Express, 14, 11848-11854, 2006.
[19] FRANCO, M. A. R., RUGGIERI, M. T., SERRAO, V. A., SIRCILLI, F., ABE, N. M. Photonic crystal fiber for chromatic dispersion compensation, Procceding SPIE, 5622, 955-960, 2004.
[20] HUANG, W., HAUS, H. Analysis of buried-channel waveguides and couplers: scalar solution and polarization correction, Journal Lightwave Technology, 8, 642-648, 1990.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2009 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.

















