FUNCIONES DE VULNERABILIDAD Y MATRICES DE PROBABILIDAD DE DAÑO SÍSMICO PARA EDIFICACIONES DE MAMPOSTERÍA UTILIZANDO TÉCNICAS DE SIMULACIÓN
Palabras clave:
Funciones de Vulnerabilidad Sísmica, Matrices de Probabilidad de Daño Sísmico, Mampostería, Funciones de Vulnerabilidad Simuladas, Matrices de Probabilidad de Daño Simuladas. (es)En este trabajo se presenta una metodología para definir el daño producido por un sismo de determinado nivel en edificaciones de mampostería por medio de la generación de funciones de vulnerabilidad simuladas. La metodología propuesta consiste en utilizar un índice de vulnerabilidad y relacionarlo con un índice de daño en función de un evento sísmico determinado. El modelo de índice de vulnerabilidad correspondió al definido por Maldonado et al. 2007 en una investigación anterior, y el índice de daño fue determinado mediante una relación demanda-capacidad evaluando los esfuerzos mediante el modelo de Abrams. La construcción de las funciones requirió contar con una muestra amplia de edificaciones, para lo cual se utilizaron técnicas de simulación que permitieron disponer de 6000 edificios hipotéticos. A cada uno de los edificios hipotéticos se le calculó su índice de vulnerabilidad y su índice de daño para diferentes aceleraciones máximas desde, 0,05g a 0,25g, y con ellos se construyeron las funciones de vulnerabilidad y matrices de probabilidad de daño sísmico para cada uno de estos valores de aceleración. De esta forma, las funciones y matrices de probabilidad de daño permiten conocer el daño que pueden alcanzar las edificaciones de mampostería para un evento de un determinado valor de aceleración máxima en función de un estimativo de su vulnerabilidad. Las funciones definidas en este estudio fueron utilizadas en la evaluación de los daños producidos por un sismo de determinado nivel en las edificaciones de una parte de la población del área metropolitana de Bucaramanga, en el municipio de Floridablanca.
FUNCIONES DE VULNERABILIDAD Y MATRICES DE PROBABILIDAD DE DAÑO SÍSMICO PARA EDIFICACIONES DE MAMPOSTERÍA UTILIZANDO TÉCNICAS DE SIMULACIÓN
SEISMIC VULNERABILITY FUNCTIONS AND SEISMIC DAMAGE PROBABILITY MATRICES FOR MASONRY BUILDINGS USING TECHNIQUES SIMULATION
ESPERANZA
MALDONADO RONDÓN
Universidad Industrial de Santander,
Grupo de Investigación INME, Bucaramanga, emaldona@uis.edu.co
IVÁN GÓMEZ ARAÚJO
Universidad Industrial de Santander,
Grupo de Investigación INME, Bucaramanga, igomez19@hotmail.com
GUSTAVO CHIO CHO
Universidad Industrial de Santander,
Grupo de Investigación INME, Bucaramanga, gchioch@uis.edu.co
Recibido para revisar Mayo 28 de 2007, aceptado Septiembre 02 de 2007, versión final Febrero 27 de 2008
RESUMEN: En este trabajo se presenta una metodología para definir el daño producido por un sismo de determinado nivel en edificaciones de mampostería por medio de la generación de funciones de vulnerabilidad simuladas. La metodología propuesta consiste en utilizar un índice de vulnerabilidad y relacionarlo con un índice de daño en función de un evento sísmico determinado. El modelo de índice de vulnerabilidad correspondió al definido por Maldonado et al. 2007 en una investigación anterior, y el índice de daño fue determinado mediante una relación demanda-capacidad evaluando los esfuerzos mediante el modelo de Abrams. La construcción de las funciones requirió contar con una muestra amplia de edificaciones, para lo cual se utilizaron técnicas de simulación que permitieron disponer de 6000 edificios hipotéticos. A cada uno de los edificios hipotéticos se le calculó su índice de vulnerabilidad y su índice de daño para diferentes aceleraciones máximas desde, 0,05g a 0,25g, y con ellos se construyeron las funciones de vulnerabilidad y matrices de probabilidad de daño sísmico para cada uno de estos valores de aceleración. De esta forma, las funciones y matrices de probabilidad de daño permiten conocer el daño que pueden alcanzar las edificaciones de mampostería para un evento de un determinado valor de aceleración máxima en función de un estimativo de su vulnerabilidad. Las funciones definidas en este estudio fueron utilizadas en la evaluación de los daños producidos por un sismo de determinado nivel en las edificaciones de una parte de la población del área metropolitana de Bucaramanga, en el municipio de Floridablanca.
PALABRAS CLAVE: Funciones de Vulnerabilidad Sísmica, Matrices de Probabilidad de Daño Sísmico, Mampostería, Funciones de Vulnerabilidad Simuladas, Matrices de Probabilidad de Daño Simuladas.
ABSTRACT: A methodology to define the damage resulting from a given seismic level in masonry buildings using simulated vulnerability functions is presented in this work. The proposed methodology consists in utilizing a vulnerability index correlating it to a damage index in function of a given seismic event. The vulnerability index model corresponds to the model reported formerly by Maldonado et al., 2007. The damage index was determined by a demand/capacity ratio, evaluating the stress using the Abrams’ Model. The function design process required the utilization of a wide sample of buildings. Simulation techniques allowed the running of simulation in 6000 hypothetical buildings. For each hypothetical building its vulnerability index and its damage index was calculated for different maximum acceleration values, ranging from 0,05 g to 0,25 g. Probability of seismic damage vulnerability and matrix functions were constructed with these data for each of these acceleration values.
Thus, the functions and matrixes of damage probability contributed to understand the damage that masonry buildings might endure in a given value of maximum acceleration in function of its vulnerability estimate. The functions defined in this study were utilized in the assessment of damages produced by a seism of a given level in buildings located at a sector of the Metropolitan Area of Bucaramanga at the Municipality of Floridablanca.
KEYWORDS: Seismic vulnerability functions, Seismic damage probability functions, Masonry, Simulated vulnerability functions, Simulated damage probability matrixes.
1. INTRODUCCIÓN
El resultado final en un estudio de vulnerabilidad es el índice de daño que sufriría una tipología estructural específica, sometida a una determinada acción sísmica. Este resultado puede obtenerse mediante dos procedimientos: el primero por medio de las denominadas matrices de probabilidad de daño, y el segundo a través de las funciones de vulnerabilidad. Los principales métodos utilizados para la generación de las matrices de probabilidad de daño o funciones de vulnerabilidad, difieren básicamente en los datos de entrada y en la forma como se obtienen las probabilidades asociadas a cada estado de daño; estos métodos pueden ser experimentales, analíticos o estar basados en observaciones de campo o en la opinión de expertos. Dependiendo de la información con la que se cuente se podrá utilizar uno u otro método, o se podrán combinar. En el caso de aplicación a ciudades colombianas como las del Área Metropolitana de Bucaramanga, no se contaba con registros de datos reales ni con información experimental, por lo cual se tomó la decisión de utilizar técnicas basadas en opinión de expertos combinadas con procesos analíticos.
De esta manera, las opiniones de expertos fueron utilizadas para la definición del índice de vulnerabilidad, y los procesos analíticos se aplicaron en la estimación del daño.
2. MATRICES DE PROBABILIDAD DE DAÑOLas matrices de probabilidad de daño expresan una probabilidad discreta de la distribución de daño, para un tipo de estructura y una intensidad sísmica dada. Es decir, expresan la probabilidad condicional P[D=j{i}] de obtener un nivel de daño en una determinada tipología igual a j, dado un terremoto de tamaño i.
Entre los principales aportes en este sentido se destacan las matrices de probabilidad de daño propuestas en el documento ATC-13 (1985), el cual se basa en el juicio y la experiencia de eminentes expertos en la materia. En el ATC-13 se presentan matrices de probabilidad de daño para más de 40 tipologías de edificaciones, además de otros tipos de estructuras como puentes, presas, túneles etc. La acción sísmica se define a través de la escala de intensidad modificada de Mercalli para los grados comprendidos entre VI y XII. Se plantean 7 estados discretos de daño con un factor central de daño.
3. FUNCIONES DE VULNERABILIDADUna función de vulnerabilidad es una relación matemática que expresa de forma continua el daño que puede sufrir un tipo de estructura específico, cuando se somete a una solicitación sísmica de determinado nivel. Las funciones de vulnerabilidad se deducen por medio de una regresión estadística de los datos de daño observado o generadas artificialmente. Una de sus principales variantes la constituyen las funciones de vulnerabilidad que relacionan un índice de vulnerabilidad con un índice de daño, condicionado por un parámetro que describe el movimiento del terreno; este parámetro puede ser la aceleración máxima Aa, o una de las escalas de intensidad sísmica, tales como MSK y MMI.
Las funciones de vulnerabilidad pueden ser observadas o calculadas (Caicedo et al.. 1994). Las observadas se basan en información existente de registros de daño debidos a sismos, a diferencia de las simuladas, que dada la falta de esta información, simulan las características de las edificaciones para evaluar el daño.
Dentro de las funciones de vulnerabilidad observadas se encuentran las propuestas por Guagenti y Petrini (1989), que relacionan el índice de vulnerabilidad, daño y aceleración del terreno, en edificaciones de mampostería con parámetros estimados en las edificaciones de las comunidades italianas de Venzone, Tarcento, San Daniele y Barrea; de tal manera que el daño se basa en una relación lineal y los coeficientes de correlación varían de acuerdo con la vulnerabilidad y se expresan en función de la Aceleración máxima en el terreno, Aa.
Otras funciones propuestas son las elaboradas por Angeletti et al. (1988) que establece unas funciones de vulnerabilidad construidas a partir del análisis de levantamientos de daño después de los terremotos de las localidades de Venzone y Barrea en Italia, cuya regresión incluye la vulnerabilidad de la edificación y unos coeficientes que dependen de la intensidad sísmica MCS.
Yépez (Yépez, 1996) generó funciones de vulnerabilidad a través de la simulación de estructuras de mampostería y hormigón armado. El estudio partió de realizar un análisis post-terremoto después de la ocurrencia de dos sismos en la región de Almería en 1993 y 1994 (al sudoeste de España), cuya máxima intensidad fue estimada de VII en la escala MSK. Este estudio se basó en el levantamiento de daño y vulnerabilidad para estructuras de hormigón armado y mampostería no reforzada, utilizando los formularios (Formulario Nivel 1 para daño y Nivel 2 para vulnerabilidad) propuesto en la metodología italiana planteada por Benedetti y Petrini, 1984. Luego de calcular los índices de daño y vulnerabilidad, procedió al análisis estadístico, obteniendo una función de vulnerabilidad de grado tres para mampostería no reforzada ante una acción sísmica cuya intensidad se estimó de VII en la escala de MSK. Dado que con base en los levantamientos de daño solo fue posible obtener una función de vulnerabilidad para una intensidad de grado VII, fue necesario recurrir a la simulación. Para ello primero generó una función de vulnerabilidad simulada para una intensidad de grado VII, para calibrarla con la observada. Una vez terminado el proceso de simulación de la función de vulnerabilidad para la intensidad VII, procedió a realizar otras funciones para los grados de intensidad VI, VIII, IX.
4. METODOLOGIA PARA LA SIMULACIÓN DE LAS FUNCIONES DE VULNERABILIDAD
El procedimiento realizado para la definición de la función de vulnerabilidad en el presente trabajo se basó en un análisis del comportamiento de las edificaciones ante un terremoto, a través de la simulación de estas, realizando el siguiente procedimiento:
- Generación aleatoria de los parámetros que intervienen en la determinación de la vulnerabilidad sísmica de las edificaciones de mampostería, los cuales son considerados como los de mayor influencia en la respuesta sísmica de las edificaciones de mampostería.
- Cuantificación de la vulnerabilidad a través del índice de vulnerabilidad (Maldonado et al., 2007, UIS-Alcaldía Floridablanca, 2006) el cual relaciona el grado de vulnerabilidad y los valores de importancia de los parámetros.
- Determinación del cortante de piso que actúa en cada nivel (FHE), que se utiliza como solicitación lateral del piso en el caso de edificios con flexibilidad despreciable del diafragma. Para los restantes casos se calcula únicamente el cortante basal en el piso.
- Cálculo del índice global de daño para cada nivel, ante diferentes solicitudes sísmicas, utilizando el modelo de Abrams (Abrams, 1992).
- Relación de los valores del índice del vulnerabilidad con el índice de daño para cada acción sísmica definida.
5. METODOLOGÍA PARA LA EVALUACIÓN DEL ÍNDICE DE VULNERABILIDAD
El modelo utilizado para estimación de la vulnerabilidad dentro de la construcción de las funciones de vulnerabilidad y matrices de probabilidad de daño es el planteado por Maldonado et al. (2007) y descrito en UIS-Alcaldía Floridablanca (2006), que se definió a partir del método del índice de vulnerabilidad propuesto por Benedetti y Petrini (1984); el cual ha sido aplicado en ciudades diferentes a las italianas, tales como Barcelona (España) (Yépez, 1996 y Mena, 2002), Cuenca (Ecuador) (Jiménez, 2002), Concepción (Chile) (Gent et al,. 2005) entre otras.
El modelo propuesto cuantifica la vulnerabilidad sísmica de edificaciones en función de once (11) parámetros que representan la predisposición de una edificación a sufrir daño debido a un evento sísmico. Los parámetros que se encuentran en el modelo son referidos a:
- Sistema estructural,
- Calidad del sistema resistente,
- Resistencia estructural,
- Posición de la cimentación,
- Suelo y pendiente del terreno,
- Diafragmas horizontales,
- Configuración en planta,
- Configuración en elevación,
- Distancia máxima entre muros,
- Tipo de cubierta,
- Estado de conservación de la edificación.
Cada parámetro, a su vez, se encuentra dividido en tres a cuatro clasificaciones a las cuales se les asocia un grado de vulnerabilidad diferente entre A (nada vulnerable) y D (muy vulnerable). Por ejemplo; en lo referente al primer parámetro, Sistema estructural, la clasificación es la siguiente:
- Edificación en mampostería confinada en todas las plantas.
- Edificación en mampostería que no posee vigas de confinamiento en alguna de las plantas o no cuenta con columnas de confinamiento en los pisos superiores.
- Edificación en mampostería que no posee columnas de confinamiento en el primer piso o en ninguna de las plantas.
- Edificación en mampostería que no posee vigas y columnas de confinamiento en ninguna de las plantas.
El cálculo del índice de vulnerabilidad se encuentra basado en la relación del grado de vulnerabilidad de los diferentes parámetros y en su respectivo valor de importancia, los cuales fueron definidos a partir de opiniones de expertos. Al recurrir a la opinión de expertos se reconoció que esta información de opiniones, posee un alto grado de subjetividad, imprecisión e incertidumbre. Por esta razón una de las mejores alternativas para manejar este tipo de información es a través de la matemática de conjuntos difusos (Zadeh, 1965, Terano et al., 1992, Bandemer y Gottwald, 1996). Luego la aritmética difusa se utilizó para relacionar las calificaciones de cada parámetro con su respectivo valor de importancia. El método tradicional para combinar información difusa con diferentes peso o importancia es el llamado Promedio Ponderado Difuso, el cual fue utilizado en este modelo para calcular el índice de vulnerabilidad sísmica de edificaciones de mampostería, que se expresa como:
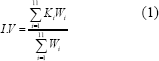
Donde IV es el índice de vulnerabilidad sísmica de la edificación de mampostería y Ki es una medida del grado de vulnerabilidad de la categoría del parámetro i. Los valores Wi son una medida de la importancia asociada con el parámetro i con respecto a los demás parámetros.
5.1 Simulación de los parámetros del índice de vulnerabilidadEn la construcción de las funciones de vulnerabilidad fue preciso simular edificaciones desde las deficientes sísmicamente hasta aquellas que poseen buenas condiciones estructurales. Para la simulación de las edificaciones fue necesario definir características como dimensiones en elevación y en planta, tamaños de los elementos estructurales, propiedades de los materiales, etc. Para las diferentes características se determinaron los límites inferior y superior. Bajo la posibilidad de generar relaciones entre las mismas características, se simuló una gran cantidad de edificaciones hipotéticas, tantas como fueron necesarias, para poder abarcar el espectro posible de combinaciones de características de una manera aleatoria.
Para la evaluación del índice de vulnerabilidad se acudió al modelo enunciado en el numeral anterior, en el cual se deben detallar diferentes parámetros para cada una de las edificaciones; por lo tanto, para la definición de la vulnerabilidad de los parámetros correspondientes al sistema estructural, posición de la cimentación, suelo y pendiente del terreno, diafragmas horizontales y tipo de cubierta, se consideraron variables aleatorias con una distribución uniforme de probabilidades.
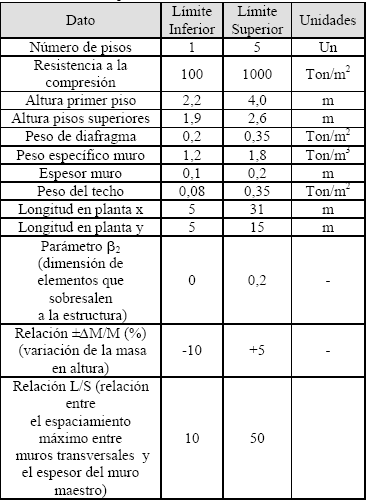
Para la evaluación de los parámetros que corresponden a la resistencia estructural, configuración en planta, configuración en elevación y distancia máxima entre los muros, se requirió conocer el valor de algunas características propias de las edificaciones reales, y para ello se tomó una muestra de 70 edificaciones de mampostería de 1 y 2 niveles ubicadas en el Área Metropolitana de Bucaramanga. Estas características con sus límites superior e inferior se presentan en la Tabla 1. Su generación aleatoria responde a una ley uniforme de probabilidades, escogiéndose cualquier valor entre los límites superior e inferior. Las dimensiones en planta de la estructura fueron utilizadas para establecer, mediante regresiones, las áreas resistentes de los muros en las direcciones ortogonales. Dichas regresiones fueron el resultado de un levantamiento detallado de edificaciones (Figura 1).
Tabla
1 . Datos y límites considerados para la evaluación de
los parámetros
Table 1. Data and boundaries considered in parameter assessment
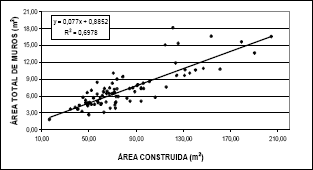
Figura
1. Área de muros resistentes total en función del
área construida
Figure 1. Area of total strength wall in function of the constructed
area
La estimación de los intervalos de los parámetros correspondientes a propiedades de materiales fueron establecidos a partir de recomendaciones de la literatura y de experiencia constructiva de la región (Niño, 1982, y Hendry, 1990).
En cuanto a los parámetros relacionados con la calidad del sistema resistente y el estado de conservación, la calificación se obtuvo relacionando los valores de esfuerzos de compresión que se generaron en el ítem anterior, calificando desde A para los valores de resistencia alta hasta D para los valores de esfuerzos bajos, descendiendo de manera proporcional; de esta manera se logró que una edificación con determinado material y cierto estado de conservación contara con propiedades que hacen que sus esfuerzos resistentes se relacionen directamente con los parámetros.
6. MODELO DE LAS EDIFICACIONES
Para la aplicación de cualquier acción sísmica siempre se requiere, en primera instancia, de una descripción del edificio mediante un modelo estructural. Es indispensable decir que la elección de un modelo depende en gran manera de las características de la estructura, la información que se posea sobre la misma, el nivel de aproximación deseado y las facilidades de cálculo disponible. Para un estudio de vulnerabilidad a gran escala a nivel de una ciudad, modelos demasiados complejos son inadecuados a causa del gran volumen de información que se necesita para generar resultados, además del esfuerzo de acopio, síntesis y procesamiento de dicha información; por consiguiente, los mejores modelos serán aquellos que, siendo sencillos, asimilen la mayor cantidad de información posible.
Teniendo como base los estudios de Moric (1986) y Tomazevic et al,. (1992) se plantearon dos tipos de modelos: a) uno que distribuye el cortante basal a cada nivel de la edificación (modelo de eje cortante) en edificaciones con un diafragma de flexibilidad despreciable; b) el modelo cuyo cortante total es aplicado a una altura H (modelo de panel) para edificaciones con flexibilidad en el diafragma. La escogencia del tipo de modelo depende de la clasificación del parámetro correspondiente al tipo de diafragma horizontal del índice de vulnerabilidad
7. METODOLOGÍA PARA LA EVALUACIÓN DEL ÍNDICE DE DAÑO
Para la evaluación del daño se tomó la metodología propuesta en el trabajo de Yépez (1996), la cual se basa en el modelo de Hasselman et al. (1980) y en la incorporación del esfuerzo máximo alcanzable, que es obtenido mediante la evaluación de capacidad lateral en el modelo de Abrams (1992). De esta forma Yépez manifiesta evaluar el daño para un muro mediante la expresión:
![]()
Donde t es el esfuerzo actuante que induce la fuerza sísmica y fv es el esfuerzo último soportable por el muro de mampostería.
Dado que el modelo de Abrams se plantea solo para paredes individualizadas, se consideró que el daño en un piso es la suma de las capacidades a carga lateral de las paredes individualizadas en la dirección considerada.
Luego las variables consideradas en el modelo tix , tiy son las demandas por carga lateral o esfuerzo cortante por sismo en nivel i o piso en consideración en la dirección correspondiente, y fvix, fviy, son las capacidades por carga lateral definidas por el modelo de Abrams en el nivel i en las direcciones X y Y, correspondientemente. De esta manera el daño en las direcciones ortogonales del piso se estima mediante las ecuaciones 3 y 4:
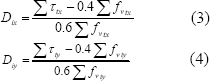
El daño definitivo del piso se establece como el máximo entre los daños de las direcciones ortogonales.
En los casos donde el daño en cualquiera de las direcciones ortogonales fue mayor de 1 se define como 1, y por otro lado, si es menor que 0 se establece como 0. Calculados los daños en cada piso se realizó una ponderación de los índices de daño por piso para calcular así el índice de daño global (Chung, 1988):
![]()
7.1 Simulación de los parámetros del índice de daño
Según el modelo teórico de Abrams, las variables necesarias
para estimar el posible comportamiento de la mampostería son el esfuerzo
de compresión (fa), la longitud total del panel (L),
el espesor del panel (b), la altura del panel (h),
el esfuerzo cortante por carga lateral (t),
la resistencia al cortante del panel (Fvo) y la resistencia
a la compresión del panel (fa). A continuación de describe
la forma en que se definieron algunas de estas variables.
Longitud unitaria del muro (L (m))
En el modelo de daño de Abrams las longitudes son referidas
a longitudes de muros, por lo cual se estableció
una distribución modular simbólica de la edificaciones para calcular longitudes
unitarias de los paneles o muros; con este fin se recurrió a los parámetros
de
área en planta A (m2) y relación aspecto b1=
Lx/Ly, del parámetro que analiza la configuración en planta
del índice de vulnerabilidad, para establecer los criterios de número de vanos
en las direcciones principales X y Y. Luego de
instaurar el número de vanos en X y Y (Vx yVy)
se cuantificó el número de muros resistentes en las direcciones ortogonales X y Y (Nx y Ny).
Posteriormente se hallaron las respectivas longitudes unitarias de los muros
en las direcciones X y Y, calculadas tanto en el
primer piso como para los pisos superiores teniendo en cuenta la irregularidades
en altura y que las áreas de los muros resistentes de los pisos superiores
pueden ser menor o mayor. De esta forma las longitudes unitarias de muros en
el primer piso son:
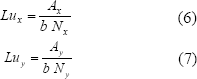
Donde Ax y Ay son las áreas de muros resistentes en el primer piso en las respetivas direcciones X y Y, b es el espesor de los muros y N es el número de muros en las direcciones X y Y. De esta manera también se definieron las longitudes unitarias de muros en los pisos superiores, considerando un aumento o disminución de áreas de muros resistentes que se establece según el parámetro de irregularidad en altura del índice de vulnerabilidad.
Esfuerzo a compresión (fa)Siendo el esfuerzo a compresión una de las variables que interviene en la capacidad de carga lateral sobre el muro, es importante establecer la diferencia entre los muros interiores y exteriores.
Por consiguiente, en la evaluación del daño se realizó la diferencia entre paredes interiores y exteriores, debido a que el esfuerzo a compresión sobre las paredes exteriores se considera la mitad en comparación con las interiores
Luego, por medio de la siguiente ecuación se calculan los esfuerzos compresivos en los muros interiores y exteriores en las direcciones principales x y y en el piso respectivo:
![]()
Donde P es la fuerza sobre el muro interior o exterior del piso en consideración i en las direcciones ortogonal respectiva, b es el espesor del muro y Lu es la longitud unitaria de los muros del primer piso o de los pisos superiores.
Esfuerzo cortante por carga lateral (t)Se establece para cada muro por medio de la ecuación:
![]()
Donde F1-n es la fuerza horizontal equivalente en el nivel de consideración n, y A x, y, xs, ys es el área de muros resistentes en las direcciones X y Y del primer piso (Ax, Ay) o de los pisos superiores (Axs, Ays).
Resistencia a la compresión (Fa)La resistencia a la compresión de los muros se redujo, por efectos de esbeltez de los muros, de la forma:
![]()
Donde Fm es la resistencia a la compresión y Re es coeficiente de reducción por esbeltez que depende de la altura del muro y el espesor.
Resistencia al cortante (Fv)Es aceptable entender que la resistencia al cortante de los muros es mayor si posee columnas de confinamiento, por lo cual la resistencia al cortante calculado para la evaluación del índice de vulnerabilidad se modifica teniendo en cuenta el primer parámetro del índice de vulnerabilidad que se refiere al confinamiento de los muros en las diferentes plantas. Para la evaluación del daño se establece que si la edificación corresponde a mampostería con columnas y vigas de confinamiento en todas las plantas, se incrementa la resistencia al cortante 40 Ton/m2 en los muros de todos los pisos, si clasifica como edificación en mampostería que posee vigas y columnas de confinamiento; pero no en todas las plantas se incrementa también la resistencia al cortante de los muros en 40 Ton/m2, a excepción del último piso.
8. PROGRAMA PDAÑO PARA LA EVALUACIÓN DE ÍNDICES DE DAÑO GLOBALES
Para el proceso de simulación del comportamiento sísmico y la respectiva evaluación del índice de daño estructural de las edificaciones hipotéticas se realizó el programa PDAÑO, el cual simula las características de las edificaciones hipotéticas y evalúa su índice de vulnerabilidad; además, calcula el daño para los dos tipos de modelos estructurales planteados.
En la siguiente figura se ilustra la estructura del programa.
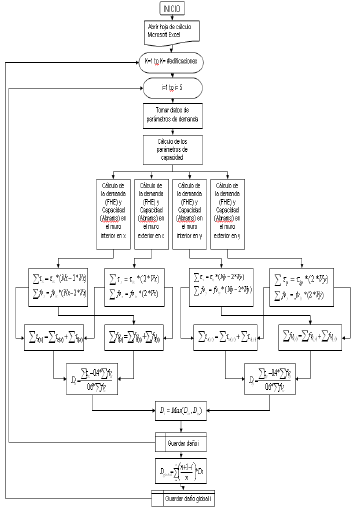
Figura 2. Diagrama de flujo general
del programa PDAÑO (Gómez y Rodríguez, 2006)
Figure 2. General flowchart of the PDAÑO program
(Gómez y Rodríguez,
2006)
9. ESTABLECIMIENTO DE LAS FUNCIONES DE VULNERABILIDAD
En las fases primera y segunda del proceso de simulación se generó de manera aleatoria el valor de cada parámetro del índice de vulnerabilidad, y posteriormente se cuantificó el índice de vulnerabilidad de cada una de las 6000 edificaciones simuladas; con estos resultados se construyó un histograma de frecuencias relativo que posee todos los datos de índice de vulnerabilidad generados (Figura 3).
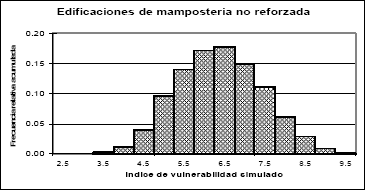
Figura
3. Histograma de frecuencias de los índices de vulnerabilidad
obtenidos en la simulación
Figure 3. Frequency histogram of vulnerability indexes obtained in
simulation
Como puede observarse en la Figura 3, los datos se aproximan a una distribución normal, cumpliendo el teorema central del límite que enuncia que si se tienen n variables aleatorias independientes (en este caso los parámetros del índice de vulnerabilidad) de modo que su distribución de probabilidad coincida, la suma de estas variables tiende a una distribución normal, aunque existen dos parámetros, 2 y 11, calidad del sistema resistente y estado de conservación, que no son independientes. Esta distribución es fundamentalmente necesaria, dado que garantiza que cada parámetro no influya más que los otros y, además, que la mayoría de las edificaciones hipotéticas generadas serán de índices de vulnerabilidad promedios y no extremos.
Después de utilizar el programa de PDAÑO se obtuvieron como resultado los puntos definidos por el índice de vulnerabilidad en abscisas, y el índice de daño en ordenadas. En vista de la gran cantidad de puntuaciones y de su gran dispersión, se optó por establecer intervalos de vulnerabilidad de 0,025, y se cálculo un índice de daño representativo de los daños de las edificaciones ubicadas y caracterizadas dentro de ese pequeño intervalo. Así pues, se discretizarón convenientemente las funciones de vulnerabilidad: cada valor de índice de vulnerabilidad (abscisa) corresponde al valor promedio de su rango correspondiente de índices de vulnerabilidades, en tanto que su ordenada de daño asociada corresponde al promedio de los daños de las edificaciones dentro del intervalo considerado. A continuación se presentan las funciones de vulnerabilidad para las edificaciones de mampostería, generadas por el proceso de simulación.

Figura 4.
Función de vulnerabilidad calculada para Aa igual a 0,02g
Figure 4. Calculated
vulnerability functions for Aa iguals 0,02g
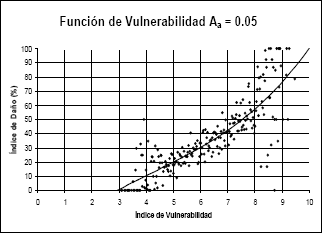
Figura 5.
Función de vulnerabilidad calculada para Aa igual a 0,05g
Figure 5. Calculated
vulnerability functions for Aa eguals 0,05g
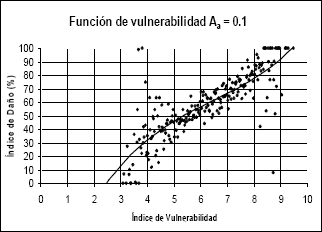
Figura 6.
Función de vulnerabilidad calculada para Aa igual a 0,10g
Figure 6. Calculated
vulnerability functions for Aa eguals 0,10g
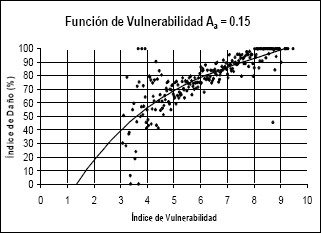
Figura 7.
Función de vulnerabilidad calculada para Aa igual a 0,15g
Figure 7. Calculated
vulnerability functions for Aa eguals 0,15g
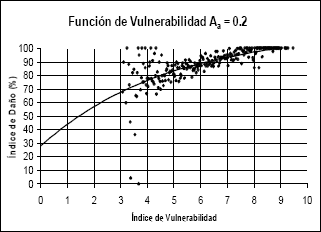
Figura 8.
Función de vulnerabilidad calculada para Aa igual a 0,20g
Figure 8. Calculated
vulnerability functions for Aa eguals 0,20g
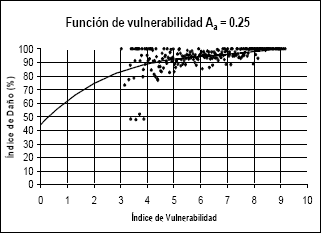
Figura 9.
Función de vulnerabilidad calculada para Aa igual a 0,25g
Figure 9. Calculated
vulnerability functions for Aa eguals 0,25g
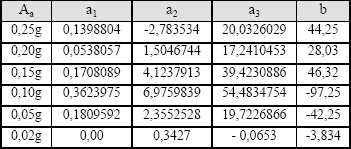
La regresión que mejor se adapta a los datos es la polinomial, en la forma que se muestra a continuación:
![]()
Los valores de las constantes a1, a2, a3, y b para cada una de las aceleraciones estudiadas se muestran en la Tabla 2.
Tabla 2. Coeficientes
de las funciones ajustadas
Table 2. Coefficients of the adjusted functions
10. MATRICES DE PROBABILIDAD DE DAÑO
Para la generación de las matrices de probabilidad de daño para las edificaciones simuladas se planteó formar frecuencias relativas de daño para cada aceleración pico efectiva, realizando discretización del daño en bandas para intervalos de vulnerabilidad también discretizados, siendo la frecuencia relativa en cada banda de daño el porcentaje con respecto al total de los daños en el intervalo de vulnerabilidad, que es también interpretado como una probabilidad de ocurrencia del daño
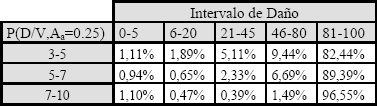
Toda la información surgida de las frecuencias de daño se resume a continuación en las matrices de probabilidad de daño para cada nivel de acción sísmica. En el eje horizontal se encuentran los intervalos de discretización del índice de daño en bandas establecidas, y en el eje vertical los intervalos del índice de vulnerabilidad considerados (filas y columnas sombreadas).
Las Tablas del 3 al 8 representan la posibilidad de obtener un índice de daño entre los dos límites, condicionada para un valor de índice de vulnerabilidad dentro de un intervalo dado y para una aceleración pico efectiva.
Tabla 3.
Matriz de Probabilidad de Daño para Aa igual a 0,02g
Table 3. Damage Probability
Matrix for Aa equals 0,02g
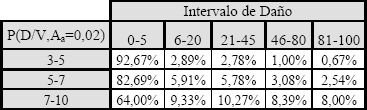
Tabla 4.
Matriz de Probabilidad de Daño para Aa igual a 0,05g
Table 4. Damage Probability
Matrix for Aa equals 0,05g
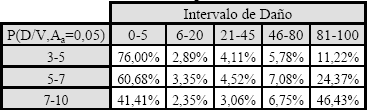
Tabla 5.
Matriz de Probabilidad de Daño para Aa igual a 0.1g
Table 5. Damage Probability
matrix for Aa equals 0.1g
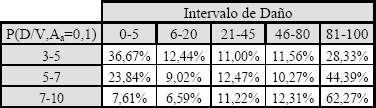
Tabla 6.
Matriz de Probabilidad de Daño para Aa igual a 0,15g
Table 6. Damage Probability
matrix for Aa equals 0,15g
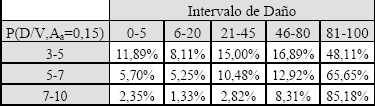
Tabla 7.
Matriz de Probabilidad de Daño para Aa igual a 0,2g
Table 7. Damage Probability
matrix for Aa equals 0,2g
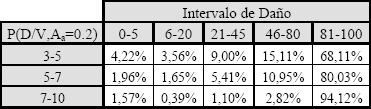
Tabla 8.
Matriz de Probabilidad de Daño para Aa igual a 0,25g
Table 8. Damage Probability
matrix for Aa equals 0,25g
11. APLICACIÓN DE LAS FUNCIONES
Las funciones fueron aplicadas para estimar los daños que se pueden producir en una zona determinada del municipio de Floridablanca, ubicada en el Área Metropolitana de Bucaramanga, ante dos posibles eventos sísmicos. La zona de estudio comprende un total de 78 barrios, con aproximadamente 760 manzanas y 12000 predios (UIS-Alcaldía Floridablanca, 2006).
Los dos escenarios sísmicos pertenecen a la Falla Bucaramanga-Santa Marta y La Frontal, que corresponden a valores de aceleración máxima de 0,16 g y 0,21 g respectivamente, los cuales a su vez pertenecen a los eventos utilizados en el estudio de Microzonificación Indicativa de Bucaramanga (INGEOMINAS, 2001).
La información de las edificaciones de la zona se recopiló a partir de encuestas realizadas a cada uno de los predios y mediante registros fotográficos. Luego los datos de cada edificación fueron incorporados en un sistema de información geográfico que facilitó el manejo y visualización de la información recopilada y de los resultados obtenidos.
Posteriormente, con la información se evaluó el índice de vulnerabilidad de cada uno de los predios; luego, con las funciones de vulnerabilidad simuladas se procedió a construir el mapa de daño para cada uno de los escenarios propuestos. En la Figura 10 se presenta el escenario de daño correspondiente a la Falla Bucaramanga-Santa Marta con una aceleración máxima de 0,16g.
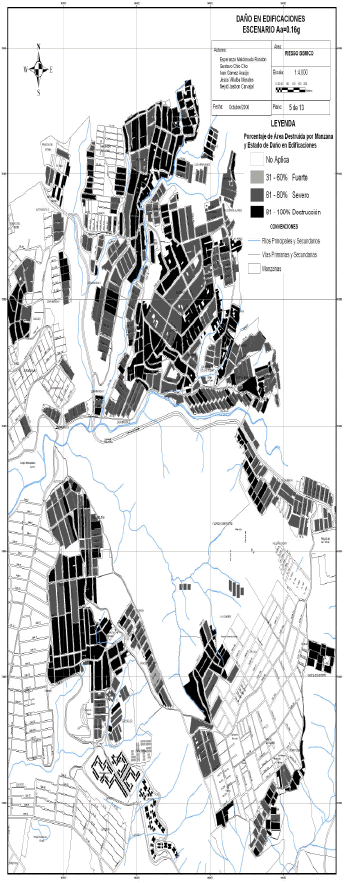
Figura
10. Escenario de daño para una aceleración de 0,16 g
Figure 10. Damage scenario for an acceleration value of 0,16 g
Estableciendo un promedio por manzana los resultados indican que un 53% de las manzanas tendrán un estado daño severo, el 44% destrucción y el 3% restante sufrirán un daño fuerte (ver Figura 11).
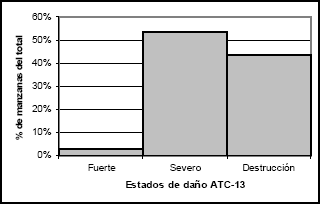
Figura 11. Estados
de daños
para una aceleración de 0,16g
Figure 11. Damage status for
an acceleration value of 0,16 g
12. CONCLUSIONES
- Mediante el presente estudio se proponen funciones de vulnerabilidad sísmica obtenidas mediante técnicas de simulación, de manera que no se requiere recurrir a datos de daños reales. Además se utiliza el método de índice de vulnerabilidad el cual es de uso general y eficiente para la evaluación de la vulnerabilidad a gran escala de edificaciones.
- La metodología propuesta en este trabajo abarca distintos aspectos de cálculo, cada uno de los cuales constituye un aporte a los modelos de evaluación de la vulnerabilidad y de daño estructural. El método involucra procedimientos de simulación de edificaciones hipotéticas que revelan las características de las estructuras reales existentes en la ciudad de Bucaramanga y su Área Metropolitana. Además, el modelo involucra procedimientos de simulación del método del índice de vulnerabilidad como mecanismo de calificación estructural.
- La simulación de miles de edificaciones ha sido posible gracias a la sencillez del modelo de índice de daño y de vulnerabilidad utilizados para la construcción de las funciones y de las matrices.
- Las funciones de vulnerabilidad fueron comparadas con las construidas por Guagenti y Petrini (1989), de manera que se encontró similitud entre ellas. Si se comparan los resultados, puede observarse una relativa similitud entre los valores, especialmente para las aceleraciones de 0,2g y 0,25g.
- Un mecanismo para evaluar el riesgo símico es el utilizar los denominados escenarios de daño, que son representaciones gráficas de todos los niveles de daño medio producidos por un sismo de un valor de aceleración determinado, haciendo uso de las funciones de vulnerabilidad sísmica obtenidas en este estudio.
- Los resultados obtenidos en la población de Floridablanca son bastante lógicos y dentro de lo que se esperaba; sin embargo es de resaltar que en la simulación de las edificaciones se utilizaron principios, fundamentos teóricos y modelos matemáticos respaldados por estudios experimentales; sin embargo, no dejan de ser modelos que contienen algunas hipótesis y simplificaciones, cuyos resultados necesitan ser calibrados con datos reales.
REFERENCIAS
[1] ABRAMS,
D. P. Strength and behavior of unreinforced masonry elements. Proceedings of
the Tenth World Conference on Earthquake Engineering, Madrid, España, 1992.
[2] ANGELETTI, P., BELLINA, A., GRANDORI, E., MORETTI, A. Y PETRINI,
V. Comparison between Vulnerability Assesement and Damage Index, Some Results,
Proceeding of the Ninth World Conference on Earthquake Engineering, Tokyo,
Japón, 7, 181-186, 1988.
[3] ATC, Applied Technology Council. Earthquake damage evaluation data for California, ATC-13, Redwood City, California, USA , 1985.
[4] BANDEMER H. Y GOTTWALD S. Fuzzy sets, fuzzy logic, fuzzy methods with applications. Jhon Wiley and Sons, New York, 1996.
[5] BENEDETTI, D. Y PETRINI, V. Sulla vulnerabilitá sísmica di edifici in muratura: Proposte di un método di valutazione, L’industria
delle Costruzioni, 149, 66-78, Roma, Italia, 1984.
[6] CAICEDO, C., BARBAT, A., CANAS, J. A. Y AGUIAR, R. Vulnerabilidad
sísmica de edificios. Monografías de Ingeniería Sísmica, Monografía CIMNE IS-6, Editor A. H. Barbat, España,
1994.
[7] CHUNG, Y.S., SHINOSUKA, M. Y MEYER, C. Automated seismic design of reinforced concrete building, Technical Report NCEER-88-0024, National Center for Earthquake Engineering Research, State University of New York at Buffalo, 1988.
[8] GENT, K., ASTROZA, M. Y GIULIANO, G. Calibración del índice de vulnerabilidad del GNDT a las edificaciones chilenas: Estructuras de albañilería confinada. Congreso Chileno de Sismología e Ingeniería Antisísmica, IX Jornadas, Concepción,
Chile, 2005.
[9] GÓMEZ, I. Y RODRÍGUEZ, E. Generación de funciones de vulnerabilidad para edificaciones de mampostería no reforzada de baja altura utilizando técnicas de simulación, Trabajo Final de Carrera, Escuela de Ingeniería
Civil. Universidad Industrial de Santander, Bucaramanga, Colombia, 2006.
[10] GUAGENTI, E. Y PETRINI, V. II caso delle vecchie costruzioni: verso
una nuova legge danni-intensità. Proceedings of the 4th Italian, National Conference
on Earthquake Engineering, Milan, Italy, Tomo I, 145-153, 1989.
[11] HASSELMAN, T., EGUCHI, R. Y WIGGINS, J. Assessment of Damageability for
Existing Buildings in a Natural Hazards Environment, Technical Report No. 80-1332-1,
J. H. Wigging Company, California, 1980.
[12] HENDRY, A.W. Structural Masonry, MacMilan Education Ltd., Londres, Inglaterra,
1990.
[13] INGEOMINAS, Subdirección de Amenazas Geoambientales, Zonificación sismogeotécnica
indicativa del Área Metropolitana de Bucaramanga. Bogota, Colombia, 2001.
[14] JIMÉNEZ, J. Vulnerabilidad sísmica de las edificaciones de la ciudad
de Cuenca mediante técnicas de simulación, Tesis de grado de Maestría. Escuela
Politécnica Nacional, Quito, Ecuador, 2002.
[15] MALDONADO, E., CHIO, G. Y GÓMEZ, I. Índice de vulnerabilidad sísmica
en edificaciones de mampostería basado en la opinión de expertos, Artículo en
revisión, 2007.
[16] MENA, U. Evaluación del Riesgo Sísmico en Zonas Urbanas, Tesis Doctoral.
Universidad Politécnica de Cataluña, Barcelona, España, 2002.
[17] MORIC, D. Possibility of making calculation simple earthquake damage
level. Proceeding of the Eighth European Conference on Earthquake Engineering.
Lisboa, Portugal, 41-48, 1986.
[18] NIÑO, L. Comportamiento de Muros de Mampostería bajo Carga Sísmica,
Trabajo final de carrera. Universidad Industrial de Santander, Bucaramanga, Colombia,
1982.
[19] TERANO, T., ASAI, K. Y SUGENO, M. Fuzzy system theory and its aplications, Academic press, Boston, 1992.
[20] TOMAZEVIC, M., VELECHOVSKY, T. Y WEISS, P. The effect of interventions in the floor structural system on the seismic resistance of historic stone-masonry buildings: An experimental study, Proceeding of the Tenth World Conference on Earthquake Engineering, Madrid, 9, 5321-5626, 1992.
[21] UIS y Alcaldía de Floridablanca. Metodología para la evaluación del riesgo debido a amenazas naturales en zonas urbanas de ciudades colombianas. Caso de estudio Floridablanca. Fase I Riesgo sísmico. Convenio ínter
administrativo 012-2006.
[22] YÉPEZ, F. Metodología para la evaluación de la vulnerabilidad y riesgo sísmico de estructuras aplicando técnicas de simulación, Tesis Doctoral. Universidad Politécnica de Cataluña, Barcelona, España,
1996.
[23] ZADEH, L. A. Fuzzy sets, Information and control, 8, 1965.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2008 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.

















