RECONSTRUCCION DE OBJETOS CON SUPERFICIES TIPO 2-VARIEDAD DIFERENCIABLE
En este artículo se propone un método para la reconstrucción de objetos con superficies tipo 2-variedad diferenciable, mediante la utilización de una red de parches de superficies NURBS, ensamblados de forma adecuada.
El particionamiento, para la red de parches, se hace en el plano de proyección, mediante la cuadrilaterización de una triangulación planar de Delaunay, representada como un grafo. Posteriormente, a estos cuadriláteros se le ajustan superficies NURBS, las cuales son proyectadas al espacio original del objeto, mediante una t馗nica punto a punto.
Los resultados se presentan para las diferentes etapas del método de reconstrucción. El tiempo empleado para el particionamiento cuadrilateral depende del número de puntos en el grafo de Delaunay y del número de ejes en el borde del modelo. Este tiempo para grafos con un número elevado de puntos de control, no supera algunos segundos.
Por ejemplo, para 58 puntos de control y 570 vecindarios es de 0,032s.
RECONSTRUCCION DE OBJETOS CON SUPERFICIES TIPO 2-VARIEDAD DIFERENCIABLE
RECONSTRUCTION OF OBJECTS WITH SURFACES TYPE 2-VARIETY DIFFERENTIABLE
ERNESTO CUARTAS
Universidad Nacional de Colombia, Sede Manizales, ecuartasm@unal.edu.co
FLAVIO PRIETO
Universidad Nacional de Colombia, Sede Manizales, faprietoo@unal.edu.co
Recibido para revisar Diciembre 10 de 2007, aceptado Abril 24 de 2008, versión final Mayo 05 de 2008
RESUMEN: En este artículo se propone un método para la reconstrucción de objetos con superficies tipo 2-variedad diferenciable, mediante la utilización de una red de parches de superficies NURBS, ensamblados de forma adecuada. El particionamiento, para la red de parches, se hace en el plano de proyección, mediante la cuadrilaterización de una triangulación planar de Delaunay, representada como un grafo. Posteriormente, a estos cuadriláteros se le ajustan superficies NURBS, las cuales son proyectadas al espacio original del objeto, mediante una técnica punto a punto. Los resultados se presentan para las diferentes etapas del método de reconstrucción. El tiempo empleado para el particionamiento cuadrilateral depende del número de puntos en el grafo de Delaunay y del número de ejes en el borde del modelo. Este tiempo para grafos con un número elevado de puntos de control, no supera algunos segundos. Por ejemplo, para 58 puntos de control y 570 vecindarios es de 0,032s.
PALABRAS CLAVE: Reconstrucción 3D, Cuadrilaterización, Superficies NURBS.
ABSTRACT: It is proposed a method for the reconstruction of objects with surfaces type 2-variety differentiable, by using a network of NURBS patches, assembled of suitable form. The quadrilateralization, for the network of patches, becomes in the projection plane, by means of a Delaunay triangulation represented like a graph. Later, the NURBS surfaces are adjusted to these quadrilaterals, and then they are projected to the original space of the object, by using a point to point technique. Results are shown for each stage of the method. The time employed for the quadrilateralization depends on the number of points in the Delaunay graph and on the number of axes in the contour of the model. This time, for graphs with an elevated number of control points, is not longer than some seconds. For instance, for 58 control points and 570 axes this time is about 0,032s.
KEYWORDS: 3D Reconstruction, Quadrilateralization, NURBS Surfaces.
1. INTRODUCCIÓN
Las funciones NURBS son empleadas para la reconstrucción de superficies de forma libre debido a su alto grado de adaptación y su representación suave y continua. Sin embargo, el paradigma del modelado mediante B-Splines está limitado, debido a que los puntos de control sobre el modelo a recrear deben estar organizados en
una estructura matricial ordenada. Este problema hace que no sea útil el ajuste de una sola superficie B-Spline, a un modelo complejo con morfología irregular. La reconstrucción eficiente requiere la introducción de una red de parches que se unan entre sí de forma adecuada, para aproximar la superficie cambiante del modelo. La generación automática de la red y la Parametrización de los puntos sobre cada parche
Es un problema complejo, debido a que la representación final depende de un proceso de particionamiento adecuado del modelo (cuadrilateral). Además, se debe garantizar la continuidad de plano tangente en las fronteras de los parches adyacentes.
Si bien se han presentado muchos trabajos orientados a la reconstrucción de objetos de forma libre, a nuestro conocimiento, estos trabajos están orientados a la cuadrilaterización y reconstrucción de objetos cerrados. Sin embargo, en muchos casos, no se requiere la reconstrucción de un objeto completo (cerrado), sino de una vista parcial proyectable a un plano, es decir una superficie tipo 2-variedad diferenciable. Estas superficies tienen la propiedad que cada punto proyectado a un plano, sólo mapea un punto de la superficie en el espacio. Ejemplo de estos objetos son máscaras, rostros, etc. El método de reconstrucción propuesto en este trabajo, se aplica al tipo de objetos que se pueden proyectar a planos. Estas proyecciones pueden presentar bordes irregulares y agujeros. El método emplea colecciones de funciones NURBS, ensambladas de forma suave, para la obtención de una representación paramétrica de la vista parcial.
Este manuscrito está estructurado de la siguiente manera: En la Sección 2. se hace una rápida revisión de estado del arte sobre la reconstrucción de superficies. Se describe, en la Sección 3., el método de cuadrilaterización de las superficies proyectadas en el plano. En la Sección 4. se presenta el método utilizado para el ajuste de superficies NURBS a los cuadriláteros y su proyección al espacio. Las dos últimas secciones presentan los resultados y las conclusiones del trabajo.
2. LA RECONSTRUCCION DE SUPERFICIES, ESTADO ACTUAL
Si se retoma el problema de la reconstrucción de superficies después de una etapa de registro de múltiples imágenes de rango, este se puede definir de la siguiente manera: “Dado un conjunto p de imágenes alineadas y con ruido: fi, , fp, encontrar la superficie que mejor aproxime los puntos contenidos en las imágenes de rango” [1].
La reconstrucción de superficies mediante funciones paramétricas NURBS es tratada por diversos autores [2,3,4,5,6,7,8,9,10]. Esta reconstrucción requiere que los puntos de control sobre el modelo a representar, estén organizados en una estructura matricial ordenada, que permita reconstruir un objeto completo y cerrado sobre sí mismo. La generación automática de esta estructura matricial, sólo parece haber sido resuelta recientemente mediante el uso de la Teoría de Morse [11,12]. A continuación presentaremos brevemente algunos de los trabajos más relevantes. En [12] se encuentra una revisión detallada del problema de reconstrucción de superficies de piezas complejas.
Kyu y Uk [5,6] desarrollan una técnica de reconstrucción, valiéndose de un algoritmo K-medias para encontrar un modelo con particiones poliédricas. A partir de este modelo se obtiene una reconstrucción triangular, conectando los vértices y el centroide de cada parche poliédrico. Finalmente, la reconstrucción triangular es apareada para encontrar una división cuadrilateral del modelo. Este particionamiento genera un gran número de vecindarios, y por lo tanto un número elevado de parches.
Eck y Hoppe [4] proponen un método de particionamiento cuadrilateral, para la parametrización del modelo. A partir de la nube de puntos, se genera una reconstrucción poligonal inicial M0. Esta reconstrucción inicial es particionada en vecindarios irregulares mediante el algoritmo de Voronoi. Al particionamiento se le aplica la triangulación de Delaunay, con la restricción de un número par de triángulos, que garantiza el apareamiento [13,14]. Finalmente, la base triangular es apareada para construir el particionamiento cuadrilateral del modelo [15]. Este método se aplica sólo a modelos cerrados sin agujeros o bordes irregulares. Contrariamente, el método que se propone en este trabajo, está orientado a superficies abiertas, cuya representación puede poseer huecos y bordes irregulares.
Dong et al [11] presenta una solución al problema de cuadrilaterización usando funciones propias del Laplaciano, las cuales son los armónicos naturales de la superficie. Ellos obtienen una representación cuadrilateral del objeto cuyos vértices son obtenidos como el conjunto de puntos críticos de una función de Morse. La teoría discreta de Morse [16] garantiza que, sin importar la complejidad topológica de la superficie representada por la malla triangular, siempre es posible obtener una representación cuadrilateral de ella.
Branch et al [17] proponen un método de recostrucción que también utiliza los puntos críticos de una función de Morse para la cuadrilaterización. En este trabajo, que también es aplicable a cualquier topología del objeto, los parámetros de las diferentes superficies NURBS son optimizadas usando estrategias evolutivas.
Estos métodos, si bien resuelven el problema de cuadrilaterización y reconstrucción de objetos cerrados y con formas complejas, son muy costosos computacionalmente. En efecto, el tiempo requerido para hallar la cuadrilaterización puede ser de muchos minutos. En el método propuesto la cuadrilaterización es realizada en el plano donde el objeto es proyectado. El tiempo para obtener esta cuadrilaterización es, en general, de unos pocos segundos. El método se aplica solo a objetos que pueden ser proyectados en un plano.
3. PARTICIONAMIENTO CUADRILATERAL DE SUPERFICIES EN PLANOS
La reconstrucción de un modelo útil mediante funciones NURBS, requiere la introducción de una red de parches ensamblados de forma adecuada. Debido a esto, se hace necesario particionar el conjunto de datos inicial. El proceso de particionamiento propuesto se aplica a modelos con las siguientes características: i) Las representaciones deben ser vistas de objetos que puedan ser mapeadas hacia un plano. ii) La disposición de los puntos en el conjunto de datos puede ser totalmente desordenada. iii) La triangulación inicial del modelo a reconstruir debe ser correcta, es decir que un borde como máximo pertenece a dos triángulos, y no debe contener triángulos aislados.
3.1 Proyección del modelo al plano
Los datos 3D del objeto a reconstruir pueden estar compuestos
por una o más imágenes de rango registradas. Ellos son proyectados a su plano
principal. El conjunto de datos inicial es rotado para que dicho plano coincida
con el plano z = 0, y los datos son
trasladados para que su centroide coincida con el origen. Sobre los datos 3D proyectados
en el plano, se obtiene una representación triangular, utilizando el algoritmo
de triangulación planar de Delaunay [14]. La triangulación es interpretada como
un grafo, donde los arcos son los bordes de cada triángulo (que llamaremos ejes
para diferenciarlos del borde del objeto), y los nodos son los vértices (v) de cada triángulo.
3.2 Extracción del borde
Partiendo de un modelo inicial triangulado, se extrae tanto
el borde exterior como los bordes de los agujeros. La Figura 1. ilustra la representación
triangular de un conjunto de puntos en el plano. Esta representación triangular
en el plano se denomina abierta [18]. En este caso, los triángulos interiores
(en color verde), tendrán siempre un triángulo vecino por cada eje, por lo
tanto: v = 3 vecinos de eje. En
contraste, los triángulos exteriores (en color rojo), los cuales contienen bordes
del contorno, tendrán 1 ≤ v <
3 triángulos vecinos de eje. Además, cada triángulo que contenga un eje del
borde, siempre tendrá 2 triángulos vecinos que contengan ejes del borde [14].
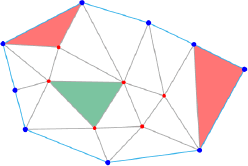
Figura 1. Triángulos de borde
Figure
1. Edge triangles
Debido a la presencia de agujeros en el objeto, pueden existir triángulos de borde que no pertenezcan al borde exterior, sino al de algún agujero. El borde exterior de la triangulación se obtiene a partir del triángulo de borde más alejado en una de las direcciones ortogonales del plano (x o y). Partiendo de este triángulo, se halla, siguiendo una dirección definida, el triángulo adyacente que pertenece al borde. Este proceso se repite hasta llegar al triángulo inicial. Los bordes de agujeros se determinan siguiendo un procedimiento similar [19].
3.3 Particionamiento
cuadrilateral
Se utiliza un esquema de particionamiento mediante la
triangulación planar de Dealuany [14], donde cada triángulo del grafo de
Delaunay se divide en 3 cuadriláteros. El grafo de Delaunay siempre tiene una
envolvente convexa, que contiene los ejes y vértices del borde. Esta envolvente
permite generar los vecindarios del borde del modelo.
3.3.1 Vecindarios cuadrilaterales a partir del grafo de Delaunay
Los vecindarios cuadrilaterales son obtenidos al fraccionar
cada una de las caras triangulares, en tres cuadriláteros (Figura 2.). Es decir, se adicionan nuevos ejes, que conectan el
centroide del triángulo, con los puntos medios de sus tres ejes.
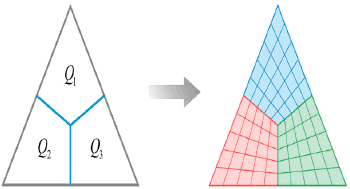
Figura 2. Partición de un
triángulo en tres cuadriláteros
Figure 2. Partition of a
triangle in three quadrilaterals
3.3.2 Vecindarios cuadrilaterales sobre los bordes
Los vecindarios cuadrilaterales
sobre los bordes, en general irregulares, son construidos con la ayuda de una
figura convexa inscrita al interior del borde del modelo. A partir de la figura
convexa, se trazan ejes radiales que corten el borde del modelo.
La Figura 3. muestra los dos casos posibles en el trazado de los ejes radiales. Para el caso con ejes angulares (Figura 3(a).), el vector radial R está dado por la suma reflejada de los vectores V1 y V2 (R = −( V1 + V2)). En el caso de ejes paralelos (Figura 3(b).), R está dado por la rotación de uno de los vectores Vi (R(x)=Vi(y) y R(y)=Vi(x)).
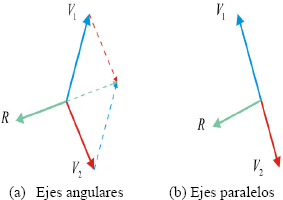
Figura 3. Proyección de los ejes de la envolvente
convexa
Figure 3. Projection of the convex hull axes
Cada uno de los ejes radiales es proyectado hasta encontrar el punto de corte con el borde del modelo. Un eje radial puede cortar el borde del modelo en varios puntos, es debido a los agujeros. Por lo tanto, se escoge el punto de corte que produzca la menor distancia euclídea. Los vecindarios generados por los ejes radiales y el borde del modelo triangulado, aunque irregulares, son parametrizables. Es decir, en ellos se puede generar una matriz ordenada, que permita aplicar una función NURBS a un vecindario con un borde irregular. La Figura 4. ilustra un ejemplo de generación de cuadriláteros irregulares, que contienen el borde del modelo a representar.
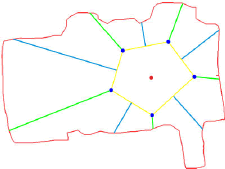
Figura
4. Cuadrilaterización de un modelo
Figure 4. Model quadrilateralization
3.3.3 Vecindarios cuadrilaterales en los agujeros
Al igual que en el borde del modelo, para recrear la forma
cambiante de los bordes en los agujeros, se generó una construcción especial
que permite particionar el modelo, rastreando la geometría del borde sobre sus
agujeros. El procedimiento propuesto caracteriza el borde sobre un agujero
aislado, y halla su eje principal. A partir de este, se construye una cara
rectangular que encierre totalmente al borde del agujero. Dicho cuadrilátero,
es particionado en cuatro cuadriláteros, para que el diseño se acople a la
partición generada por la triangulación.
La Figura 5. muestra el particionamiento propuesto para los agujeros. Cada esquina del cuadrilátero generado, es un punto de control (nodo) en el grafo, para así tener un acople adecuado dentro de la cuadrilaterización global.
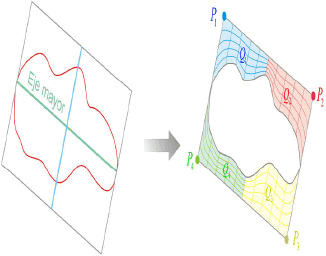
Figura 5. Particionamiento de agujeros
Figure 5. Hole quadrilateralization
4. AJUSTE DE SUPERFICIES NURBS
El ajuste de una superficie NURBS, a un cuadrilátero, requiere la definición de: el valor de los pesos, el vector de nodos y los puntos de control. En el método propuesto, se definen inicialmente los pesos con un valor unitario. Posteriormente, ellos son optimizados con un método como el propuesto en [19]. Para el vector paramétrico de nodos, en todos los parches, se asume una disposición regular. Debido a que de la optimización de este vector, no disminuye en forma considerable el error en la aproximación, y el costo computacional es alto [20]. Por lo tanto, el proceso de parametrización se reduce a encontrar los puntos de control.
4.1 Selección de puntos de control en el plano
Partiendo de la proyección planar de los datos, se generan
redes de control en los vecindarios cuadrilaterales de la partición. Para un
ajuste efectivo de la continuidad entre parches NURBS se definen, en el proceso
de parametrización, el mismo número de puntos de control en la dirección u y en la dirección v [4]. La forma general de las superficies B-Splines (con pesos
unitarios), se presenta en la Ecuación 1.
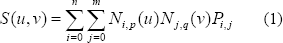
Las funciones base Ni,p y Nj,q son calculadas mediante una expansión regular de nodos. Por lo tanto, los parámetros a determinar son los puntos de control Pi,j. Estos puntos se deben ordenar en un arreglo matricial Sp, con n puntos de control en la dirección u y m puntos en la dirección v. En este método m = n. Para garantizar un ordenamiento efectivo, se etiqueta un eje del cuadrilátero como eje inicial, y los demás se ordenan en dirección contraria a las manecillas del reloj.
4.1.1 Caso
cuadrilatero regular
Las caras cuadrilaterales generadas al interior del grafo
de Delaunay son regulares, debido a que todos sus lados rectos. En este caso se
escoge, arbitrariamente, uno de los ejes como eje inicial, y se etiquetan los
demás ejes en sentido anti-horario. En la Figura 6. ilustra una
parametrización con n puntos de control
en en las dos direcciones paramétricas.
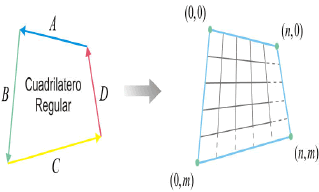
Figura 6. Parametrización de un cuadrilátero regular
Figure 6. A regular quadrilateral Parametrización
Dados los ejes A, B, C y D, donde cada eje tiene dos vértices e = (a, b) y cada vértice se encuentra en el plano, y dado un número de divisiones ndiv en ambas direcciones paramétricas, se tiene que:
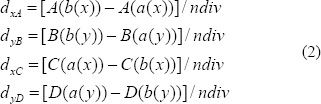
En donde dxA y dxC son los incrementos en la dirección x y, dyB y dyD son los incrementos en la dirección y.
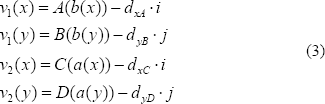
v1(x) y v2(x) son los valores incrementales en la dirección u, y v1(y) y v2(y) los valores incrementales en la dirección v.
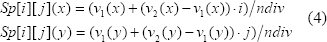
Donde i = 1, 2, . . . , ndiv + 1 y j = 1, 2, . . . , ndiv + 1, son las variables de indexación de la matriz de puntos de control Sp. La Ecuación 4. define la matriz de puntos de control para los vecindarios cuadrilaterales regulares.
4.1.2 Caso cuadrilatero irregular
El caso irregular se presenta en los cuadriláteros
dispuestos en la parte exterior del grafo de Delaunay, tanto los del borde
exterior del modelo, como los vecindarios que caracterizan los agujeros al
interior del mismo. Este tipo de vecindario tiene tres lados rectos y un lado
irregular que forma parte del borde del modelo. Como en el caso regular, se
escoge uno de los ejes como eje inicial y se etiquetan los demás ejes en
sentido anti-horario. Dicho eje inicial ya no es arbitrario, sino que
corresponde al lado opuesto al eje irregular del cuadrilátero. De esta forma,
el lado irregular siempre estará dispuesto en la misma posición de los cuadriláteros
irregulares en la partición.
A partir del particionamiento del eje inicial, y del segmento de recta que une los vértices extremos del eje irregular, se generan ejes auxiliares. Estos son extendidos hasta llegar al eje irregular, para encontrar los puntos de control en la parametrización.
En la Figura 7. se aprecia la parametrización para el caso irregular. Los puntos de control se obtienen al dividir los ejes auxiliares, por el número de particiones que se requiera en la dirección paramétrica v.
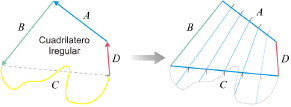
Figura 7. Parametrización de
un cuadrilátero irregular
Figure 7. A irregular quadrilateral Parametrización
Dados los ejes A y C (eje que une los vértices extremos del borde irregular), donde cada eje tiene dos vértices y cada vértice se encuentra en el plano, y dado un número de divisiones ndiv en ambas direcciones paramétricas, se tiene que:
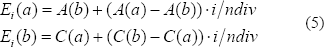
Donde Ei son los ejes auxiliares que cortan el eje irregular del vecindario, Ei(a) es el vértice a del eje Ei sobre el eje A, y Ei (b) es el vértice b del eje Ei sobre el eje C. La Ecuación 6. define la matriz de puntos de control para los vecindarios cuadrilaterales irregulares.
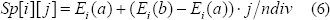
Donde i = 1, 2, . . . , ndiv + 1 y j = 1, 2, . . . , ndiv + 1, son las variables de indexación de la matriz de puntos de control Sp.
4.1.3 Agujeros
La metodología de parametrización para el caso de los
agujeros es la misma que para el caso de los vecindarios irregulares del borde
exterior del modelo. No obstante, el borde analizado en el caso específico de
los agujeros, es el borde del agujero y no el del contorno. Esto se logra al
etiquetar los vecindarios irregulares del borde exterior y de los agujeros, en
el modelo planar a parametrizar.
4.2 Mapeo 2D a 3D
El paso siguiente para recrear el mapeo 3D del objeto a
reconstruir es proyectar los puntos de control, de cada una de las
parametrizaciones planares de los cuadriláteros, al espacio. En la estrategia
de mapeo 3D punto a punto, se debe encontrar para cada uno de los puntos de
control, el punto más cercano en la proyección planar de la nube de puntos.
Posteriormente, se traza una recta paramétrica en el espacio en la dirección del
eje z, la cual pasa por el punto de control en la parametrización, esta recta
es interceptada por el plano que genera el punto más cercano en la nube y su
normal. El punto sobre el plano, que pertenezca a la recta paramétrica dada,
será la proyección 3D sobre la superficie implícita en la nube de puntos.
La Figura 8. muestra el esquema de la proyección 3D punto a punto, en donde Pparam es un punto de control en la parametrización planar, PPcer es el punto (proyectado al plano) más cercano a Pparam, dist es la distancia entre Pparam y PPcer, R es la recta paramétrica 3D que pasa por Pparam y es paralela al eje z. PEcer es el punto más cercano en el espacio, N es la normal asociada a dicho punto y π es el plano generado por el punto PEcer y su normal N. La proyección 3D punto a punto PPP, está dada entonces por la intersección entre la recta paramétrica R y el plano π.
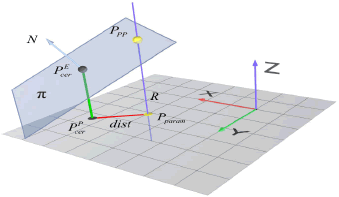
Figura 8. Proyección 3D punto a punto
Figure 8. Point to point 3D projection
La ecuación del plano π está dada por:
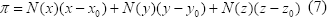
Recordamos que PEcer = (x0, y0, z0) y N = (N(x), N(y), N(z)). La ecuación general de la recta paramétrica R = R(λ) es:

Donde A y C son 2 puntos sobre la recta, los cuales pueden ser obtenidos tomando 2 valores diferentes para la coordenada z en el punto Pparam. La representación homogénea de R es:
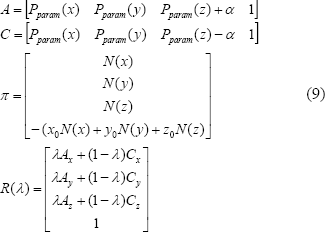
Si un valor de λ en la recta paramétrica R(λ), corresponde a un punto en el espacio que pertenezca al plano π, entonces se cumple que

Mediante la Ecuación 10. es posible encontrar el valor λ en R(λ) que intercepte el plano π, ya que debido a la proyección planar de los datos, las normales en la reconstrucción inicial nunca generan planos paralelos a R(λ), que no contengan por lo menos un punto común entre π y R(λ).
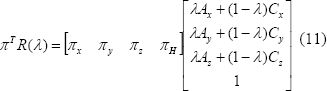
Al reemplazar p por el de la Ecuación 9. e igualar a cero, se obtiene λ, como:
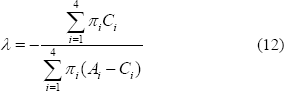
Dado que los valores en A y C de las coordenadas x e y son iguales, se puede simplificar la Ecuación 12., hasta obtener
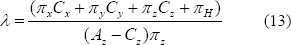
Donde πH = -(x0N(x) + y0N(y) + z0N(z)). Mediante la Ecuación 14., es posible encontrar la proyección PPP del punto Pparam sobre el plano π:
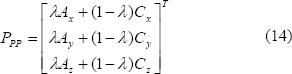
4.3 Continuidad entre funciones NURBS
La continuidad entre funciones NURBS ensambladas ha sido un
tópico de gran interés en el área de reconstrucción mediante funciones
B-Splines. Diversos autores emplean diferentes esquemas para garantizar una
continuidad de normales en los modelos reconstruidos. En este trabajo se empleó
el esquema de continuidad en B-Splines de Peters [8], como fue implementado en
[22].
Los esquemas de optimización mediante funciones NURBS se basan en la reducción del error de ajuste, el cual es medido entre la nube de puntos y el modelo paramétrico. El algoritmo de optimización utilizado está basado en el trabajo de Elsaesser [21], y su implementación se puede encontrar en [20]. Un método que puede arrojar mejores resultados, es el propuesto por Branch [12,17], el cual realiza la optimización utilizando estrategias evolutivas.
5. EVALUACION Y RESULTADOS
En la Figura 9. se presentan los conjuntos de datos empleados para probar el desempeño de la metodología de reconstrucción propuesta. Ellos son (en orden): Rostro, compuesto por 1469 vértices y 2849 triángulos en la reconstrucción inicial. Válvula, compuesto por 12700 vértices y 25180 triángulos en la reconstrucción inicial. Buda, compuesto por 14866 vértices y 29584 triángulos en la reconstrucción inicial. Cerámica precolombina, compuesto por 26912 vértices y 53599 triángulos en la reconstrucción inicial. Máscara, compuesto por 119924 vértices y 233800 triángulos en la reconstrucción inicial.

Figura 9. Conjunto de objetos
utilizados, en orden: Rostro, Válvula (Universidad de Stanford), Buda
(Universidad de Stanford), Cerámica y Máscara (Universidad de Alberta)
Figure 9. Set of
used objects, in order: Face, Valve (
Stanford University), Buddha ( Stanford University),
Ceramics and Mask ( University
of Alberta)
Todos los algoritmos fueron implementados en C++ y apoyados en las librerías del OpenGL Versión 1.3 para la visualización de los modelos. El código fue compilado en la plataforma C++ del Visual Studio .Net 2003. El computador empleado cuenta con un procesador Intel Pentium IV de 3GHz, 1GB de memoria RAM DDR2 a 333MHz, con una tarjeta de video ATI All-In-Wonder con chip Radeon 9800 y 128MB de memoria interna.
5.1 Evaluación
del particionamiento cuadrilateral
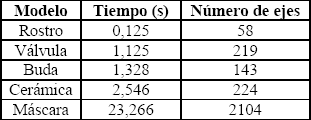
Se midió el tiempo empleado para la extracción de los bordes
de los modelos empleados (Ver Tabla 1.). El tiempo de cálculo en este algoritmo
depende en gran medida del número de triángulos en la reconstrucción inicial
del modelo. El tiempo más alto se presentó en el modelo cerámica, debido a que
la reconstrucción inicial de este tiene una mayor concentración de triángulos.
Tabla 1. Tiempo de
extracción del borde
Table 1. Time
for the edge extraction
Se emplearon dos esquemas de selección automática de puntos de control para el grafo de particionamiento de Delaunay, uno totalmente aleatorio y otro aleatorio restringido. En la selección aleatoria, se realizaron 5 pruebas, escogiendo diez puntos de control de forma aleatoria en la proyección planar de la nube de puntos, para generar el particionamiento cuadrilateral. No obstante, 3 de las pruebas arrojaron como resultado un particionamiento erróneo, debido a que el grafo de Delaunay no se encontraba inscrito al interior del borde del modelo. En la selección aleatoria restringida, se realizaron 5 pruebas más, escogiendo los puntos de control aleatorimente, pero restringidos a estar dentro de una circunferencia con origen en el centro de masa del modelo y que corta el borde del mismo. De esta forma, todos los puntos elegidos no sólo se encuentran sobre el modelo, sino que además están contenidos en la circunferencia. Esta, por ser convexa, garantiza que el grafo de Delaunay inscrito en su interior, esté totalmente contenido por el borde del modelo.
La Figura 10. ilustra el proceso de selección aleatoria de puntos de control, en el particionamiento cuadrilateral. En la izquierda se muestra un caso erróneo, donde la envolvente convexa del grafo de Delaunay no está inscrito al interior del borde del modelo. En la derecha se muestra, como los puntos aleatorios dispuestos dentro de la circunferencia de restricción, generan una partición correcta.

Figura 10. Selección de los
puntos de control
Figure 10. Control points
selection
El tiempo empleado para el particionamiento cuadrilateral es muy bajo. Este no depende del número de muestras en los conjuntos de datos, sino del número de puntos de control en el grafo de Delaunay y del número de ejes en el borde del modelo. Incluso para esquemas con un número elevado de puntos de control, el tiempo de cálculo del algoritmo no supera algunos segundo. Para 58 puntos de control y 570 vecindarios, el cálculo del particionamiento tardó 0,032s.
5.2 Parametrización
Al igual que en el particionamiento, el tiempo empleado
para la selección de puntos de control en el plano, durante el proceso de
parametrización, es muy pequeño. Este no depende del número de datos en el
modelo a reconstruir, sino del número de cuadriláteros en el particionamiento,
del número de ejes en el borde del modelo y del número de divisiones que se
requieran en ambas direcciones paramétricas. En un modelo con 494 vecindarios,
y 100 divisiones en cada dirección paramétrica (10000 puntos de control sobre
cada vecindario), el tiempo promedio del cálculo, para el caso regular fue de
0,878ms y, para el caso irregular de 6,84ms. El tiempo total de cálculo fue de 0,625s.
Se encontró que el tiempo empleado en el proceso de proyección 3D (punto a punto), era grande. Esto, debido a que se deben encontrar los datos objetivos en un conjunto extenso, para cada punto de control en la parametrización planar. Para solucionar este problema se generó un algoritmo de indexación cuadrada, que se encarga de almacenar los puntos de control en una estructura matricial, de acuerdo a su posición en el plano. De esta manera, para un punto dado en la parametrización, sólo se debe analizar un conjunto reducido de muestras, que corresponde a los puntos en la nube que se encuentran más cercanos a dicho punto, y por tanto son candidatos a proyección.
En la Figura 11. se aprecia la diferencia en el tiempo de cálculo entre la indexación cuadrada y la búsqueda sobre el espacio de datos completo. Para la búsqueda en todo el espacio, el tiempo de cálculo aumenta exponencialmente con el número de divisiones. En la indexación cuadrada, este tiempo presenta un comportamiento lineal con una pendiente muy pequeña, lo que produce tiempos menores. En la figura el tiempo está dado en segundos.
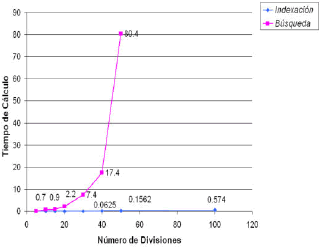
Figura 11. Tiempo empleado en la Parametrización
Figure 11. Time used for the Parametrización
5.3 Reconstrucción completa
La Figura 12. muestra la reconstrucción del modelo cerámica mediante el
método propuesto.
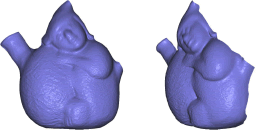
Figura 12. Reconstrucción del
modelo cerámica
Figure 12. Reconstruction of the ceramics model
El particionamiento cuenta con 53 cuadriláteros, de los cuales 14 son irregulares y pertenecen al borde exterior del modelo. El tiempo empleado para el particionamiento fue de 0,016s. Se emplearon 30 divisiones en cada dirección paramétrica para el proceso de parametrización. El tiempo empleado para la parametrización fue de 4,797s. En la reconstrucción inicial, el error en la aproximación fue de 0,0123, el cual luego de aplicar el proceso de optimización se redujo hasta 0,0046. El tiempo de cálculo de la optimización fue de 7832s.
La Figura 13. muestra la reconstrucción del modelo máscara. El particionamiento cuenta con 32 cuadriláteros, de los cuales 20 son irregulares, 12 pertenecen al borde exterior del modelo, y 8 pertenecen a la caracterización de los agujeros. El tiempo empleado para el particionamiento fue de 0,012s. Se emplearon 20 divisiones en cada dirección paramétrica para el proceso de parametrización. El tiempo de la parametrización fue de 23,478s. En la reconstrucción inicial, el error en la aproximación fue de 0,0532, el cual luego de aplicar el proceso de optimización se redujo hasta 0,0154. El tiempo de cálculo de la optimización fue de 4254s.

Figura 13. Reconstrucción
del modelo máscara
Figure 13. Reconstruction of the mask model
6. CONCLUSIONES
Se presentó un método de reconstrucción de objetos con superficies tipo 2-variedad diferenciable. El método realiza una cuadrilaterización de las superficies proyectadas en el plano principal, mediante el uso del grafo de Delaunay. Posteriormente, se ajustan superficies NURBS a estos cuadriláteros y se proyectan al espacio original.
El particionamiento cuadrilateral de conjuntos de datos en el plano, se realiza mediante la construcción de un vecindario de Delaunay, y la proyección de ejes radiales para rastrear la forma de los bordes. A partir del grafo de Delaunay se crean vecindarios cuadrilaterales, partiendo cada triángulo en tres cuadriláteros. Además, la envolvente convexa del grafo, permite crear vecindarios cuadrilaterales en el borde del modelo.
La proyección de los datos al plano, permite generar redes de control matriciales ordenadas, en cada uno de los vecindarios de la partición cuadrilateral. Además, el rastreo de bordes irregulares y agujeros en el modelo, se simplifica en gran medida en este espacio planar. Sobre las redes de control matriciales ordenadas, se pueden aplicar directamente funciones paramétricas como NURBS o B-Splines. Además, mediante los métodos de proyección implementados se puede aproximar la información tridimensional de vistas parciales de modelos tridimensionales.
El modelo de reconstrucción propuesto ofrece un método de multiresolución directo, ya que es posible ajustar el nivel de detalle de la parametrización, variando la cantidad de puntos de control, para obtener modelos más detallados o más livianos.
REFERENCIAS
[1] B. CURLESS. “New Methods for Surface Reconstruction from Range Images”. PhD thesis, Stanford University, Stanford, USA. (1997).
[2] C.W. ANDERSON; CRAWFORD-HINES. “Fast generatión of NURBS surfaces from polygonal mesh models of human anatomy”. Technical Report Technical Report CS-99-101, Department of Computer Science, Colorado State University, Fort Collins, USA . (2000).
[3] M. RANDRIANARIVONY; G. BRUNNETT. “Parallel implementation of surface reconstruction from noisy samples”. SFB preprint 02-16, Technische Universitat Chemnitz. (2002).
[4] M. ECK; H. HOPPE. “Automatic reconstruction of b-spline surfaces of arbitrary topological type”. In Proceedings of the 23rd annual conference on Computer graphics and interactive techniques, pages 325–334. ACM Press. (1996).
[5] KYU PARK; S. UK LEE . “Constructing NURBS surface model from scattered and unorganized range data”. Second International Conference on 3D Imaging and Modeling. Ottawa, Canada . October 4-8. (1999).
[6] KYU PARK; S. UK LEE . “Geometric model from scattered 3d range data”. Seoul National University. (1998).
[7] C. LOOP. “Smooth Spline surfaces over irregular meshes”. Computer Graphics, pages 303–310. (1994).
[8] J. PETERS. “Constructing Cl surfaces of arbitrary topology using bicuadric and bicubics splines”. Designing Fair Curves and Surfaces, pages 277–293. (1994).
[9] K. HORMANN. “From scattered samples to smooth surfaces”. Technical report, California Institute of Technology. USA. (2002).
[10] K. MAEDA; M. KUMAMARU. “Shapes modeling of 3d objects based on a hybrid representation using extended B-Spline surface model”. IEEE Pattern Recognition. (2002).
[11] S. DONG; P. BREMER; M. GARLAND; V, PASCUCCI; J. HAR. “Quadrangulating a mesh using Laplacian eigenvectors”. Technical report, University of Illinois, USA (2005).
[12] J.W. BRANCH. “Reconstrucción de objetos de forma libre a partir de imágenes de rango usando superficies NURBS por pedazos”. PhD Tesis, Universidad Nacional de Colombia Sede Medellín, Colombia. (2007).
[13] D.M. MOUNT. “Voronoi diagrams on the surface of a polyhedron”. Technical Report CAR-TR-121, University of Maryland, Department of Computer Science. (1985).
[14] M. DE BERG; M. VAN KREVELD. “Computational Geometry, Algorithms and Applications”. Springer-Verlag, Second Edition. (2000).
[15] T. HOPPE; H. ECK; M. DEROSE. “Multiresolution analysis of arbitrary meshes”. Computer Graphics, pages 173–782. (1995).
[16] S. DONG; P.T. BREMER; M. GARLAND; V. PASCUCCI; J.C. HART. “Spectral surface quadrangulation”. In SIGGRAPH 2006: ACM SIGGRAPH 2006 Papers, pp. 1057–1066. ACM Press, New York. USA . (2006).
[17] J.W. BRANCH; F. PRIETO; P. BOULANGER. “Automatic Extraction of a Quadrilateral Network of NURBS Patches From Range Data Using Evolutionary Strategies”. In Lecture Notes in Computer Science, Springer-Verlag Berlin, Heidelberger, Germany , Vol. 4842. ISVC2007. Pages 701-710, November (2007).
[18] G. FARIN. “Shape”. Springer-Verlag, New York. USA . 3 Edition. (2001).
[19] E CUARTAS. “Reconstrucción de superficies de forma libre mediante funciones NURBS”. MSc Tesis. Universidad Nacional de Colombia Sede Manizales. Manizales, Colombia. (2006).
[20] E. CUARTAS; F. PRIETO. “Optimización de superficies NURBS mediante el algoritmo de levemberg-marquardt”. Reporte técnico, Universidad Nacional de Colombia sede Manizales, Manizales, Colombia. (2004).
[21] B. ELSAESSER. “Approximation whit Rational B-Splines Curves and Surfaces”. PhD thesis, Vanderbilt University, Nashville, USA . (1998).
[22] E. CUARTAS; F. PRIETO. “Análisis de continuidad entre funciones NURBS”. Revista Avances en Sistemas e Informática, Vol. 3 No. 2, Universidad Nacional de Colombia Sede Medellín, Medellín, Colombia, Páginas 19-23. Diciembre de (2006).
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2008 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.
















