Using Dispersion Measures for Determining Block-Size in Motion Estimation
Palabras clave:
Motion estimation, block matching, variance, mean absolute deviations, variable block-size (es)USING DISPERSION MEASURES FOR DETERMINING BLOCK-SIZE IN-MOTION ESTIMATION
USANDO MEDIDAS DE DISPERSIÓN PARA DETERMINAR EL TAMAÑO DEL BLOQUE EN LA ESTIMACIÓN DE MOVIMIENTO
CARLOS MERA
MSc., PhD. Student, Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, campus Medellín, camerab@unal.edu.co
MARIA TRUJILLO
PhD., Professor, Escuela de Ingeniería de Sistemas y Computación, Universidad del Valle, Cali, maria.trujillo@correounivalle.edu.co
Received for review July 20th, 2011, accepted December 2th, 2011, final version December, 21th, 2011
ABSTRACT: Video compression techniques remove temporal redundancy among frames and enable high compression efficiency in coding systems. Reduction of temporal redundancy is achieved by motion compensation. In turn, motion compensation requires motion estimation. Block matching is perhaps the most reliable and robust technique for motion estimation in video coding. However, block matching is computational expensive. Different approaches have been proposed in order to improve block matching motion estimation accuracy and efficiency. In this paper a block-matching strategy for motion estimation is introduced. In the proposed approach the size of matching block is adapted according to the variability of the matching areas. That is, the block size is constrained by variations of the image intensity. The variability is assessed using two variability measures: the variance and the mean absolute deviation. Results of computer experiments aimed at validating the performance of the proposed approach are also reported.
KEYWORDS: Motion estimation, block matching, variance, mean absolute deviations, variable block size
RESUMEN: Las técnicas de compresión de video disminuyen la redundancia temporal entre los fotogramas del video para realizar una compresión eficiente del mismo. Dicha reducción se logra mediante la compensación de movimiento, la cual está basada en la estimación de movimiento. Block matching es quizás la técnica más robusta y fiable para la estimación de movimiento, en compresión de video. Sin embargo, el block-matching es un proceso computacionalmente costoso. Diferentes enfoques han sido propuestos con el fin de mejorar la precisión y la eficiencia del block-matching. En este trabajo se presenta una estrategia de block-matching para la estimación de movimiento. En el enfoque propuesto el tamaño de los bloques se determina teniendo en cuenta las variaciones de las intensidades de la luz en las regiones de los fotogramas. Las variaciones de las intensidades de la luz se evalúa usando dos medidas de variabilidad: la varianza y la desviación media absoluta. Los resultados experimentales muestran un mejor desempeño de los algoritmos de block-matching usando el enfoque propuesto.
PALABRAS CLAVE: Estimación de movimiento, block-matching, varianza, desviación media absoluta, bloques de tamaño variable
1. INTRODUCTION
Motion estimation (ME) is the basis for motion compensation and removes temporal redundancies among frames in video coding systems [1,2]. Motion estimation usually counts for up to 70-80% of the computational complexity of a complete encoding system [3,4]. Although several approaches have been presented in the literature to determine the best choice of motion vectors, the block-matching algorithm (BMA) is the most popular. The BMA divides an image frame into blocks of size N x N and matches each block in the reference frame to the most similar block within a search area in the next frame assuming that all the pixels within a block have uniform translational motion. However, the use of fixed-size blocks has some drawbacks; when small block size is used, it may produce problems of ambiguity; and on the other hand, a large block size may cause inaccuracy problems. In addition, the boundaries of moving objects do not normally coincide with the boundaries of the blocks used for motion estimation [4,5].
Unlike the BMA, variable block-size (VBS) motion estimation is a method where the block size is varied according to the types of motion in the block. Accuracy in motion estimation can be improved by coding blocks of high motion detail, using a small block size. Similarly, blocks with less motion detail can be encoded using larger block sizes [6].
Only a few approaches adaptively change the size of the matching block. A pioneering work in this direction was introduced by Levine et al. [7] in the early 1970s. In this work, the block size is adapted according to variations in intensity values. Vaisey and Gersho [8] discussed techniques in which the size of the block is varied according to the local detail of the image using quad-tree implementation. Puri et al. [9] presented a decision rule for determining the block size based on the comparison of motion compensated prediction error between two different block sizes. Oh and Lee [10] used a top-down partition within an image segment in order to establish a homogenous block. However, the homogeneity criterion is not included in the discussion. In [5] and [11], a VLSI architecture for VBS, and a VLSI processor with parallel architecture based on an adaptive block size are proposed, respectively. Veksler [12] proposed a variable block algorithm using integral images and defining a block cost, based on average error and variance, which explores a range of block shapes and sizes. In [4] the authors proposed an algorithm for adaptive selection of block sizes based on measuring texture areas as a criterion to stop the reduction of the block size for visually irrelevant areas.
The computer-vision community has also addressed the problem of block size. Kanade and Okutomi [13] proposed an iterative algorithm that controls the size and the shape of the block using a measure of the uncertainty in the motion/disparity estimation. Tzovaras et al. considered using two multiresolution block-matching methods where the size of the block varies with the resolution level of the frame [14]. Fusiello et al. presented a multi-block algorithm using nine asymmetric matching blocks, where the motion/disparity profile is used to select the appropriate size [15]. Ohm et al. [16] as well as Izquierdo [17] proposed a hierarchical block matching algorithm which uses large size blocks in the first level and small size blocks in the second level for refining the initial estimation. Although they proposed to use different block sizes, they are fixed heedless of the frame/image content. For continuous optimisation, Goulermas et al. [18] introduced a new regularisation to enforce the inter-block dependency. Odone, Trucco, and Verri [19] presented a method using matching blocks, based on dilation along the grey values and the spatial dimension, taking into account variations in grey levels and localization. In [20], a modified semivariogram function was introduced, which takes into account spatial variations for constraining the block size, in a feature-based matching strategy.
The H.264 standard [21,22] allows variable block sizes to be used in motion estimation. In H.264, a frame is first divided using macro-blocks (MB) of size 16x16. Each MB may then be segmented into micro-blocks (mB) of block sizes 8x16, 16x8, 8x8, 8x4, 4x8, and 4x4. These smaller blocks intend to describe complex motion and movements next to objects edges. Although this standard gives the ability to dynamically choose what block size will be used, the block size is predetermined and fixed.
In this paper, an approach for adaptively selecting the block size is proposed. The approach exploits intensity variation using relevant statistical measures. Intensity variations within macro and micro-blocks are compared in order to decide whether to perform a new partition. Experimental evaluations showed better estimations of motion vectors by using an appropriate block size.
This paper is organized as follows: Section 2 gives a brief discussion of the block-matching motion estimation and commonly used variability measures. The block-size estimation criterion is introduced in Section 3. Experimental evaluations and final remarks are presented in Sections 4 and 5, respectively.
2. BACKGROUND
Let  and
and  be adjacent video frames at t and t + 1. Block-matching is described as follows and illustrated in Fig. 1. Given a point
be adjacent video frames at t and t + 1. Block-matching is described as follows and illustrated in Fig. 1. Given a point , a reference block of size
, a reference block of size  x
x 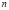 is positioned on
is positioned on 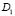 with
with  at the left-up corner. A search area of size
at the left-up corner. A search area of size  x
x is defined on
is defined on  with
with  at its centre. A matching operation is performed between the reference block in
at its centre. A matching operation is performed between the reference block in  and all matching blocks lying within the search area in
and all matching blocks lying within the search area in . This matching is based on a search for the most similar matching block within the search area in
. This matching is based on a search for the most similar matching block within the search area in  using a similarity measure, for instance mean absolute differences (MAD) or mean squared error (MSE) [23].
using a similarity measure, for instance mean absolute differences (MAD) or mean squared error (MSE) [23].

Figure 1. Conventional block-matching techniques
Estimated displacement vectors are calculated by the difference between the left-up point at the reference block in  ,
,  , and the left-up point at the most similar matched block within the search area in
, and the left-up point at the most similar matched block within the search area in  ,
,  . That is:
. That is:

As mentioned before, the matching block size depends on the spatial variability in the surrounding areas. When there is large variability in the surrounding areas, a small matching block is required. On the other hand, when there is small variability in the surrounding areas, a large matching block is needed. Assessing variations in the surrounding areas can be done by means of a variability measure. A large number of variability measures have been explored in the literature [24]. The most frequently used are the range, the interquartile range, the variance, the coefficient of variation, and the standard deviation.
We consider most relevant statistical measures for establishing a homogeneous matching block based on deviations of intensity values from the mean and from the median within a block. The variance is calculated as the average of the squared deviations from the mean, using Norm-2. The absolute deviation is calculated as the average of the absolute deviations from the median, using Norm-1. Higher-order statistics are not considered since they are used for assessing shape rather than variations.
The following notation is used: Let I(x,y) be an intensity value of a pixel (x, y) lying within a block of size  x
x .
.  and Me represent, respectively, the mean and median of the intensity in such a block.
and Me represent, respectively, the mean and median of the intensity in such a block.
The variance can be seen as a measurement of global variations around the mean. These variations can be measured in a region regardless of the spatial location of the intensity value in the frame. The use of the variance assumes outcomes to be independent.

The coefficient of variation (CV) is a normalized measure of dispersion [25] useful to compare dispersions at different scales.

The mean absolute deviation can be seen as a measurement of global variations around the median. These variations can be measured in a region regardless of the location of the frame intensity. The use of the mean absolute deviation assumes outcomes to be independent and it assures robustness against noise.

Selected blocks and their intensity values, in Fig. 2, are used to illustrate how the measures can be used to assess homogeneity in a block. The green block has homogeneous intensity values, and the blue one does not have them. Table 1 shows the variance, coefficient of variation and mean absolute deviation, computed for the blocks of Fig. 2. It can be observed that small values of these measures indicate small variations in intensity values. Therefore, we can detect homogeneous blocks by comparing the values obtained in the two blocks.

Figure 2. Illustration of intensity values in two selected 8x8 blocks
Table 1. Values of Var, CV, and MAD calculated using the blocks of Fig. 2

3. THE BLOCK-SIZE ESTIMATION
Homogeneous blocks can be detected by comparing the intensity variation in a large area with the intensity variation in small areas lying within the large area. Large areas are called macro-blocks (MB) and small areas are called micro-blocks (mB). The homogeneity of an area is assessed using a variability measure such as: the variance, the coefficient of variation, and the mean absolute deviation.
In this work, we use a quad-tree approach to structure a partition of the image. In a quad-tree, each node represents a block and has four children, unless it is a leaf. A parent node is an MB, and their children are mBs which have a quarter of the area of its parent. This structure is depicted in Fig. 3.

Figure 3. A quad-tree approach used
At each node a test is performed to evaluate if the mB represented by the node is homogeneous by comparing the intensity variation of that mB and its parent. If the test is positive the node becomes a left, otherwise the node becomes a MB and it is divided. The partition strategy is described in detailed as follows using the subsequent notation:
- Var(MBk) is the value of the variance in the k-th MB.
- Var(mBki) is the value of the variance in the i-th mB within the k-th MB.
- CV(MBk) is the value of the coefficient of variation in the k-th MB.
- CV(mBki) is the value of the coefficient of variation in the i-th mB within the k-th MB.
- MAD (MBk) is the value of the mean absolute deviation in the k-th MB.
- MAD(mBki) is the value of the mean absolute deviation in the i-th mB within the k-th MB.
Initially, a median filter is used to homogenise the content in the frame and reduce the effect of noise and textures. Then, as it is illustrated in Fig. 4, the whole frame content is divided into four MBs (MBk). Then, each MB is divided in four mBs (mBki). Homogeneity in an mB is assessed by variability measures in order to decide whether or not to subdivide each mB (mBki). In this way, we use w, whose value is equal to one (w == 1) when the i-th mB, within the k-th MB (mBki), is not homogeneous and it must be subdivided into new four mBs.

Figure 4. Process for subdividing a frame: table tennis sequence
The w criterion is computed as follows:

Figure 4 illustrates the blocks obtained in the first frame of table tennis video sequence, when the proposed criterion is used. Figure 5 depicts the proposed algorithm.

Figure 5. Algorithm to get the variable block-size
Table 2 shows the values obtained using the selected measures in MBs and mBs of the first frame of the table tennis video sequence (step 1). It can be observed that the variability in mB14 is greater than the variability in MB1, which suggests that mB14 should be subdivided (here Eq. 7 is used). Human visual perception, in Fig. 4, shows that mB12 must be subdivided too. If the values of mB12 are compared with the values of MB1, it can be seen that these values are close.
Table 2. Numerical Information about MB and mB in the first step using the first frame of table tennis video sequence

The values in Table 2 suggest that when the CV value of the MB is greater than 0.1, mBs may be subdivided (Eq. 5). A similar situation happens with the CV values of the mBs (Eq. 7). Human visual perception indicates that an mB must be subdivided when its variance is greater than or close to the variance of MB or when the MAD for an mB is greater than the MAD of an MB (Eqs. 8 and 9, respectively).
4. EXPERIMENTAL VALIDATION
The performance of the proposed method has been verified by processing various video sequences using the full search method in which the motion vector is searched at all the locations within the search window. These video sequences are available at http://media.xiph.org/video/derf/ and have different motion activity and different content. Table 3 describe the video sequences tests.
Table 3. Video sequences tests description

The blocks are obtained from the first frame and these are used for estimating motion in the shot. Results are reported using the PNSR values, time in milliseconds, and the number of blocks obtained.
The proposed algorithm efficiently partitioned the frames. The block size is small both in the surroundings of object's edges and in highly textured areas. In contrast, large block sizes are obtained in remaining areas. (This can be observed on the images in Table 4.)
Table 4. Blocks obtained with the VSB proposed algorithm

Table 5 presents the performance of the algorithm with respect to the peak signal-to-noise ratio (PSNR). When the proposed method is used, the obtained PSNR has similar compression performance. Additionally, it can be observed in Table 5 that larger blocks yield higher PSNR values.
Table 6 shows the number of blocks when fixed block sizes (4x4, 8x8, and 16x16) and variable block-size algorithms are used. The number of blocks is reduced compared to when 4x4 and 8x8 blocks are used. However, the number of blocks for the proposed technique is larger than the number of blocks when 16x16 blocks are used. This is because the proposed algorithm reduces the block size in frames with high textures, like Coastguard, Garden, Mobile, Silent, and Stefan.
Table 6. Total number of blocks for BM

Table 7 shows average computation time—in milliseconds—obtained for the test sequences using the full search algorithm with fixed block sizes (4x4, 8x8, and 16x16) and the proposed technique include the time used for dividing the frame. Results show that in most of the test sequences, the computation of motion vectors is faster.
Table 7. Average time in milliseconds

5. CONCLUSION
We consider statistic measures for establishing homogeneous matching blocks. Intensity variations were assessed by the coefficient of variation, the variance, and the mean absolute deviation. These measures rely on the assumption that intensity values are independent.
The results show that the proposed method avoids unnecessary reduction in the block size in homogeneous areas and reduces the block size in areas that contain complex motions. Subsequently, the number of blocks is reduced compared with the use of 4x4 and 8x8 blocks, and hence the number of bits for encoding all kinds of video sequences is decreased.
The average PSNR does not show significant differences between the reconstruction obtained using prefixed block size and the reconstruction obtained using variable block size. However, a reduction of the computational cost of block matching algorithm using larger block size may justify implementing the proposed approach.
ACKNOWLEDGMENTS
The first author gratefully acknowledges the support of the Universidad de San Buenaventura Seccional Cali. Most of the writing of this paper was done while he was professor at Programa de Ingeniería de Sistemas in that university.
REFERENCES
[1] ISO/IEC 11172 MPEG-1, Coding of moving pictures and associated audio for digital storage media at up to about 1,5 Mbit/s - Part 2 Video, 1993.
[2] ISO/IEC 13818 Information technology, Generic coding of moving pictures and associated audio information, Part 2: Video, 1995.
[3] Zeng, B., Li, R. and Liou, M. L., Optimization of fast block motion estimation algorithms, IEEE Transactions on Circuits and Systems for Video Technology, Vol. 7, No. 6, pp. 833-844, 1997.
[4] Gohokar, V. V. and Gohokar, V. N., Adaptive Selection of Motion Estimation Block Size for Rate-Distortion Optimization, International Journal of Computer Applications, Vol. 17, No. 4, pp. 44-48, 2011.
[5] Ou, C.-M., Le, C.-F. and Hwang, W.-J., An efficient VLSI architecture for H.264 variable block size motion estimation, IEEE Transactions on Consumer Electronics, Vol. 51, No. 4, pp. 1291-1299, 2005.
[6] Ahmad, A., Khan, N., Masud, S. and Maud, M. A., Efficient block size selection in H.264 video coding standard, Electronics Letters, Vol. 40, No. 1, pp. 19-21, 2004.
[7] Levine, M. D., O'handley, D. A. and YAGI, G. M., Computer Determination of Depth Maps, Computer Graphics and Image Processing, Vol. 2, pp. 131-150, 1973.
[8] Vaisey, D. and Gersho, A., Variable block-size image coding, in Processing of IEEE International Conference on Acoustics, Speech, and Signal, Vol. 12, pp. 1051-1054, 1987.
[9] Puri, A., Hang, H. M. and Schilling, D. L., Interframe coding with variable block size motion compensation, Proceedings of IEEE Global Telecommunications Conference, pp. 65-69, Nov-1987.
[10] Oh, H.-S. and Lee, H.-K., Adaptive adjustment of the search window for block-matching algorithm with variable block size, IEEE Tran. on Consumer Electronics, Vol. 44, No. 3, pp. 659-666, 1998.
[11] Hariyama, M., Yokoyama, N., Kameyama, M. and Kobayashi, Y., FPGA implementation of a stereo matching processor based on window-parallel-and-pixel-parallel architecture, in 48th midwest Symposium on Circuits and Systems, Vol. 2, pp. 1219-1222, 2005.
[12] Veksler, O., Fast variable window for stereo correspondence using integral images, in Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition., Vol. 1, pp. 556-561, 2003.
[13] Kanade, T. and Okutomi, M., A stereo matching algorithm with an adaptive window: theory and experiment, IEEE Tran. on Pattern Analysis and Machine Intelligence, Vol. 16, No. 9, pp. 920-932, 1994.
[14] Tzovaras, D., Strintzis, M. G. and Sahinolou, H., Evaluation of multiresolution block matching techniques for motion and disparity estimation, Signal Processing: Image Communication, Vol. 6, pp. 56-67, 1994.
[15] Fusiello, A., Roberto, V. and Trucco, E., Efficient stereo with multiple windowing, in Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, pp. 858-863, 1997.
[16] Ohm, J.-R., Izquierdo, E. and Muller, K., Systems for disparity-based multiple-view interpolation, in Proceedings of the IEEE International Symposium on Circuits and Systems, Vol. 5, pp. 502-505, 1998.
[17] Izquierdo, E., Stereo matching for enhanced telepresence in 3D video communications, IEEE Transactions on Circuits and Systems for Video Technology, Vol. 7, No. 4, pp. 629 -643, 1997.
[18] Goulermas, J. Y., Liatsis, P. and Fernando, T., A constrained nonlinear energy minimization framework for the regularization of the stereo correspondence problem, IEEE Transactions on Circuits and Systems for Video Technology, Vol. 15, No. 4, pp. 550-565, 2005.
[19] Odone, F., Trucco, E. and Verri, A., A flexible algorithm for image matching, in Proceedings of 11th International Conference on Image Analysis and Processing, pp. 290-295, 2001.
[20] Trujillo, M. F. and Izquierdo, E., Exploiting Spatial Variability for Disparity Estimation, in Proceedings International Conference in Semantic Analysis of Multimedia Technologies, 2006.
[21] Bjontegaard, G., H.26L Test Model Long Term Number 5 (TML-5) draft 0. ITU-T Standardization Sector, Doc. Q15-K-59d1, Oct-2000.
[22] Wiegand, T., Sullivan, G. J., Bjontegaard, G. and Luthra, A., Overview of the H.264/AVC video coding standard, IEEE Transactions on Circuits and Systems for Video Technology, Vol. 13, No. 7, pp. 560 -576, 2003.
[23] Cox, G. S., Template Matching and Measures of Match in Image Processing, University of Cape Town, South Africa, 1995.
[24] Sprinthall, R. C., Basic Statistical Analysis, 9th ed. Prentice Hall, 2011.
[25] Hendricks, W. A. and Robey, K. W., The Sampling Distribution of the Coefficient of Variation, The Annuals of Mathematical Statistics, Vol. 7, No. 3, pp. 129-132, 1936.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2012 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.


















