CONTROL ORIENTED MODELS OF STEP-UP AND STEP-DOWN PHOTOVOLTAIC POWER SYSTEMS
Palabras clave:
Photovoltaic systems, control systems, control-oriented model (es)CONTROL-ORIENTED MODELS OF STEP-UP AND STEP-DOWN PHOTOVOLTAIC POWER SYSTEMS
MODELADO ORIENTADO AL CONTROL DE SISTEMAS FOTOVOLTAICOS PARA APLICACIONES ELEVADORAS Y REDUCTORAS DE VOLTAJE
JUAN C. VELÁSQUEZ-VÁSQUEZ
Universidad Nacional de Colombia, GAUNAL, Medellín, jcvelasquezv@unal.edu.co
SARA YARCE-DE LOS RÍOS
Universidad Nacional de Colombia, GAUNAL, Medellín, syarcer@unal.edu.co
CARLOS ANDRES RAMOS-PAJA
Dr., Profesor de la Universidad Nacional de Colombia, GAUNAL, Medellín, caramosp@unal.edu.co
ELIANA ISABEL ARANGO ZULUAGA
Dr., Profesora Universidad Nacional de Colombia, GAUNAL, Medellín, eiarangoz@unal.edu.co
DANIEL GONZALEZ
Universidad Nacional de Colombia, GAUNAL, Medellín, dgonzalm@unal.edu.co
Received for review November 11th, 2011, accepted February 20th, 2012, final version February, 22th, 2012
ABSTRACT: This paper presents the modeling and control of photovoltaic systems considering disturbances in solar irradiance and load. Three cases are addressed: step-up/step-down systems using a non-inverting Buck-Boost converter interface, step-down systems using a Buck converter interface, and step-up systems using a Boost converter. Control-oriented models are analytically derived to design controllers that regulate the voltage of the photovoltaic panel in agreement with the reference provided by a maximum power point tracking algorithm, aimed at maximizing power production. The proposed models are validated by means of frequency response analyses, and the designed controllers are validated by means of detailed simulations performed in standard power electronics software. Finally, experimental results illustrate the applicability of the proposed approach to real cases.
KEYWORDS: Photovoltaic systems, control systems, control-oriented model.
RESUMEN: Este artículo presenta el modelado y control de sistemas fotovoltaicos considerando perturbaciones en la irradiación solar y en la carga. Se consideran tres casos: sistemas con elevación/reducción usando un convertidor Buck/Boost no inversor, sistemas exclusivamente reductores usando un convertidor Buck, y sistemas exclusivamente elevadores usando un convertidor del Boost. Los sistemas son modelados para diseñar controladores de voltaje que regulen el panel fotovoltaico de acuerdo con la referencia dada por un algoritmo para seguimiento del punto de máxima potencia, el cual busca maximizar la potencia producida. Los modelos propuestos son validados a partir del análisis de su respuesta en frecuencia, y el diseño de los controladores se validada a través de simulaciones detalladas realizadas con un simulador estándar de electrónica de potencia. Finalmente, la aplicabilidad de la solución propuesta se valida con resultados experimentales.
PALABRAS CLAVE: Sistemas fotovoltaicos, sistemas de control, modelos orientados a control.
1. INTRODUCTION
Photovoltaic (PV) systems transform solar energy into electrical energy for residential and mobile applications. In both cases, the PV panel interacts with a dc/dc converter to drive the PV voltage near the optimal operating point, named the maximum power point (MPP) [1], to extract the maximum energy from the source. Such a procedure is regulated by means of a maximum power point tracking (MPPT) controller [1]. Moreover, the dc/dc converter can be operated in two ways: in an open loop, where the MPPT controller defines the converter duty cycle [2], or in a closed loop, where the MPPT controller defines the reference of the converter voltage controller [3,4].
Figure 1 shows the typical closed-loop structure of a PV system, where the MPPT controller gives the voltage controller reference. Such a structure allows for one to mitigate the effect of environmental and load perturbations. In addition, when the PV system is connected to the grid, the dc/dc converter output exhibits sinusoidal oscillations at double the grid frequency [3] in current and/or voltage, which must be cancelled to allow for the correct tracking of the MPP [1,3].
The design of the PV voltage controller requires a proper modeling approach, which takes into account both the dc/dc converter, the PV panel, and load models. In this way, the most typical dc/dc converters used in PV applications are the boost, buck and buck-boost topologies.
For step-up applications, boost converters are widely adopted [3,5,6] due to their simplicity and step-up voltage conversion ratio. The most common application of step-up PV systems concerns the grid-connection. Similarly, for a PV step-down system, the classical buck converter is widely adopted [2], whose main application concerns battery-charging devices. The step-up/step-down PV systems are considered for distributed MPPT (DMPPT) applications, where load voltage can change depending on the PV modules' configuration (whether it be a series or parallel) [7]. In this way, the SolarMagic is a commercial example of this type of device [8].
This paper provides control-oriented realistic models for step-up, step-down, and step-up/step-down PV applications, which are useful to design the PV voltage controller. Such models take into account the parasitic resistances associated with passive elements, which significantly change system dynamics. The models are validated by means of frequency responses, simulations results, and experimental measurements.
2. MODELING CONSIDERATIONS
In PV applications, the dc/dc converters are commonly considered to be operating in continuous conduction mode (CCM) [9] since such conditions provide lower inductor current and PV voltage ripples. Therefore, discontinuous conduction mode (DCM) conditions are not discussed in this paper.
Moreover, the PV panel is modeled in a small signal condition by means of a Norton equivalent (PVM), where the current source corresponds to the PV panel short-circuit current [4]. In addition, the system load is also modeled by means of a Norton circuit, which permits one to investigate the PV system stability to load perturbations [1]. In this way, the mitigation of the grid-connection oscillations can be analyzed.
To obtain numerical results, a BP585 PV panel [10] has been adopted. Such a PV panel exhibits a Vmpp = 18 V and an Impp = 4.72 A at a solar irradiance level of 1000 W/m2, which in addition defines a PV panel short-circuit current Isc = 5A. Such numerical models were used to design PV voltage controllers to illustrate the models' applicability. Finally, the simulations consider a non-linear model of the PV panel [11] to test the designed controllers in realistic conditions.
3. STEP-UP/STEP-DOWN APPLICATIONS
This section addresses the most general configuration, which provides both step-up and step-down conditions. This solution is based on the non-inverting buck-boost dc/dc converter presented in Fig. 2. It is noted that such a converter requires four semiconductors instead of the classical Mosfet-diode pair used in buck or boost topologies.

Figure 2. Step-up/step-down PV system
3.1. State space modeling and linearization
The system dynamic model considers the classical structure given in (1). The states, inputs, and output vectors are given in (2), where iL represents the inductor current, vCi the input capacitor voltage, vCo the output capacitor voltage, isc the PV panel short-circuit current, io the disturbances on the output current, d the dc/dc converter duty cycle, and vpv the PV voltage. The system differential and output equations (3-7) were obtained by applying volt-second and charge balances [9].

The operating point calculation must be performed in terms of the desired system conditions: steady-state PV current and voltage at the MPP, Ipv = Impp, and Vpv = Vmpp. The equilibrium conditions of the system at such an MPP are found by considering the state derivatives equal to zero, and obtaining (8), where capital letters represent steady-state values.
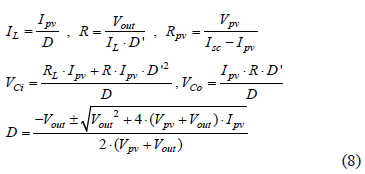
The following Eq. (9) allows for one to design the converter parameters that guarantee the desired voltage ripple conditions, where TS represents the converter switching period.
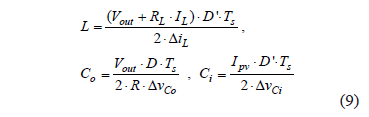
where DiL, DvCi, and DvCo represent the inductor current, and input and output voltage ripples.
To design a classical linear controller, it is necessary to linearize the system around the calculated operating point. This is performed by evaluating A, B, C, and D Jacobian matrixes at the MPP (8):

To validate the PV system model proposed in this section, the system circuit presented in Fig. 2 has been implemented in the power electronics simulator PSIM. Figures 3 to 5 present the comparison between the frequency responses of both the PSIM circuit and the Matlab model simulations. Such figures show satisfactory accuracy in the reproduction of the system state dynamics, which give evidence that the proposed model is suitable for control purposes.

Figure 3. Bode diagrams for iL

Figure 4. Bode diagrams for vCi

Figure 5. Bode diagrams for vCo
3.2. Controller design and simulation results
To ensure the operation at the MPP it is necessary for one to regulate the PV voltage. In this paper, a PI controller is designed to illustrate the model applicability. The system damping factor of the complex poles is set to z = 0.707 to provide a satisfactory tradeoff between settling time and maximum overshoot. In addition, the closed loop bandwidth has been set to Fc = Fs/5, where FS represents the switching frequency, to guarantee the validity of the model in the controller frequency range [12]. Finally, the controller has been designed by means of the pole-zero placement technique in the Laplace domain.
Adopting a desired load voltage equal to Vout = 24 V and a switching frequency Fs = 50 kHz, the converter parameters have been calculated from Eqs. (8,9): L = 150 mH, Ci = 1.13 mF, Co = 1.678 mF, RCi = 1.4 nW, RCo = 0.3 pW, RL = 10 mW, R = 6.83 W, RPV = 64.28 W, and D = 0.57. The controller designed to fulfill the given requirements is:

Figure 6 shows a root locus diagram of the system, where the complex roots fulfill the desired damping ratio (white trace). In addition, Fig. 7 presents the system loop gain and phase, where the gain margin is higher than 10 dB and the phase margin is higher than 60°, which denotes satisfactory relative stability.

Figure 7. Open-loop Bode diagram
It is noted that the gain margin is negative, but it does not imply instability since the converter exhibits negative gain and it is not a low-pass system. Moreover, the roots of the closed-loop system are negative, as reported in Fig. 6, which guarantees global stability.
Figure 8 presents the system closed-loop frequency responses, where the desired system bandwidth is achieved (TVref). In addition, such frequency responses put in evidence the mitigation of perturbation in the load current (TVio) and in the PV panel short-circuit current (TVisc), which is proportional to the solar irradiance that reaches the PV panel [11].
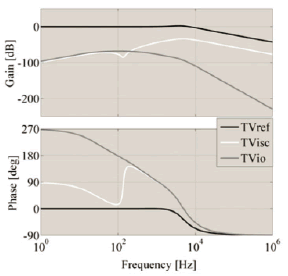
Figure 8. Closed-loop Bode diagram
The complete system, considering a non-linear PV model panel [11], was simulated in PSIM considering a Perturb and Observe MPPT controller [1] and perturbations on both load current and solar irradiance. Figure 9 shows the satisfactory simulation results, where a 100 Hz load current oscillation with an amplitude equal to 30% of the DC component was imposed. In addition, the MPPT controller provides the reference to the voltage controller aimed at maximizing the power extracted from the PV. The simulation also considers a 50% step transients in the irradiance. The simulation reports a satisfactory system response, where both perturbations are effectively rejected while the MPPT reference is accurately tracked. This satisfactory operation is observed in the three-point steady-state behavior of the PV voltage for all the irradiance conditions [1], and on the stable PV power profile in the presence of load current and voltage perturbations.
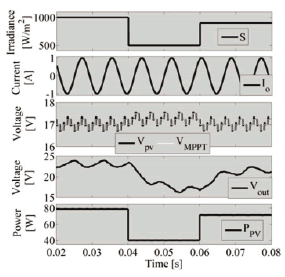
Figure 9. Step-up/step-down PV system simulation
4. STEP-DOWN APPLICATIONS
Figure 10 presents a step-down PV system based on a buck converter. Again, the PV panel and the load are modeled by means of Norton equivalents.

Figure 10. Step-down PV system
4.1. State space modeling and linearization
The dynamic model is described in state space (1,2), where a, b, d', s, r, and r are the same parameters defined in the previous section. The system operating point is calculated following the same procedure also presented in the previous section, obtaining:
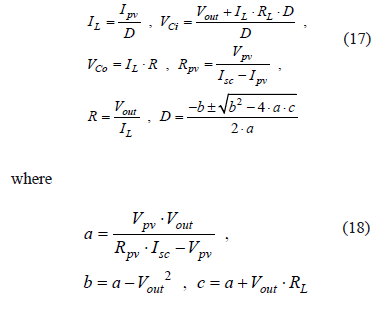
and the inductor and capacitor values to obtain the desired current and voltage ripples are

Then, the linear Jacobians around the MPP are
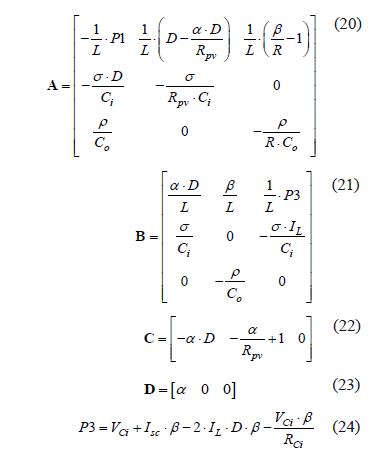
4.2. Controller design and simulation results
In this section, the design of a PID controller, adopting the same performance criteria used in the previous section, is presented: damping ratio z = 0.707 and cross over frequency Fc = Fs/5. Adopting again the conditions Vout = 12V and Fs = 50 kHz, the converter parameters are calculated from Eqs. (17-19): L = 56 mH, Ci = 800 mF, Co = 300 mF, RCi = 0.06 pW, RCo = 2 pW, RL = 17 mW, R = 1.71 W, RPV = 64.28 W, and D = 0.67. The controller designed by means of the pole-zero placement technique is
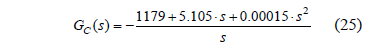
Figure 11 presents the system closed-loop frequency responses, where the desired system bandwidth is achieved (TVref), and the mitigation of the perturbations on both the load current (TVio) and the PV panel short-circuit current (TVisc), are satisfactory.

Figure 11. Closed-loop Bode diagram
Similar to the previous case, the complete system was simulated in PSIM, considering a MPPT controller and perturbations on both load and irradiance. Figure 12 shows the satisfactory simulation results, where a 100 Hz load current oscillation with an amplitude equal to 30% of the DC component was imposed. Again, the MPPT controller provides the reference to the voltage controller to maximize the power extracted from the PV, and 50% step transients in the irradiance are imposed, obtaining satisfactory results. Similar to the previous case, the three-point steady state behavior of the PV voltage and the steady PV power are observed in the presence of perturbations on the load current and voltage.

Figure 12. Step-down PV system simulation
5. STEP-UP APPLICATIONS
Figure 13 presents a step-up PV system based on a boost converter, where again the PV panel and the load are modeled with Norton equivalents.
5.1. State space modeling and linearization
Following the methodology presented in the previous sections, the dynamic model of the system is represented in state space (1-2). The operating point of the PV system is calculated from Eq. (26), and the converter parameters are calculated from (27). Moreover, the linearized system Jacobian matrices are given in (28-32).

5.2. Controller design and simulation results
In this section, the design of a PID controller, adopting the same performance criteria proposed in the previous section, is developed: damping ratio z = 0.707 and cross over frequency Fc = Fs/5. Adopting again the conditions Vout = 12 V and FS = 50 kHz, the converter parameters are calculated from Eqs. (26-27): L = 250 mH, Ci = 66 mF, Co = 480 mF, RCi = 9 pW, RCo = 0.1 nW, RL = 41 mW, R = 27.48 W, D = 0.63, and RPV = 64.28W. The controller designed to fulfill such requirements is
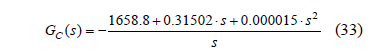
Figure 14 presents the system closed-loop frequency responses, where the desired system bandwidth is achieved (TVref), and the perturbations on both the load current (TVio) and in the PV panel short-circuit current (TVisc) are mitigated.

Figure 14. Closed-loop Bode diagram
Similar to the previous cases, the complete system was simulated in PSIM considering a MPPT controller and perturbations on both load and irradiance. Figure 15 shows the satisfactory simulation results under a 100 Hz load current oscillation with an amplitude of 30% of the DC component, and the interaction with the MPPT controller. Again, two 50% step transients in the irradiance are simulated, obtaining satisfactory results. This case also exhibits the three-point steady state behavior on the PV voltage and a stable PV power in the presence of perturbations.
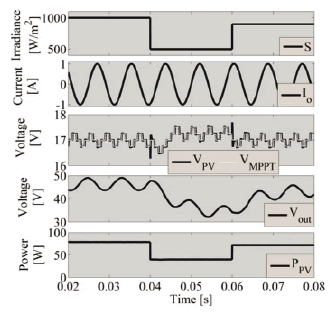
Figure 15. Step-up PV system simulation
6. EXPERIMENTAL RESULTS
The applicability of the proposed models was verified by means of experiments performed in a proof of concept PV system based on a boost converter. Such a case was selected because it requires low-side circuitry for driving the Mosfets, which simplify the implementation in comparison to the buck and buck-boost cases. The models of the PV systems based on buck and buck-boost converters have been validated in the previous sections by means of the simulation results.
Figure 16 presents the experimental test bench. The adopted boost converter was designed to use capacitors in the range of microfarads and an inductor in the range of tens of microhenry. Such a condition avoids the requirement of large passive elements. The experimental parameters are: L = 13 mH, Ci = 110 mF, Co = 66 mF, RCi = 0.1 mW, RCo = 0.1 mW, RL = 0.182 W, R = 27.48 W and RPV = 15.63 W. The operating point was calculated from (26-27), and the controller was designed to achieve a 0.707 damping factor and a 20 kHz closed-loop bandwidth. Those conditions ensure a satisfactory dynamic response, but any other conditions can be imposed. The PV voltage controller was implemented in a multipurpose control board with analog PID modules, while the voltage reference was externally generated by an MPPT controller implemented in a PC running the Matlab Real-Time Workshop.

Figure 16. Experimental test bench
Figure 17 shows the measurement obtained in the system interacting with an MPPT controller as given in Fig. 1. The experiments report a correct MPPT operation in the presence of 50% load voltage oscillations; this is illustrated by the stable 3-point PV voltage profile. Such satisfactory results verify the correctness of the PV voltage controller calculated by means of the proposed modeling approach.

Figure 17. Experimental system performance
7. CONCLUSIONS
This paper has presented control-oriented models for step-up/step-down, step-down, and step-up PV systems based on buck-boost, buck, and boost dc/dc converters. The proposed models have been validated by means of frequency responses of all the states. Such a technique is more effective for validating models in comparison with traditional step responses, since uniform excitation is applied.
The modeling approaches take into account the parasitic losses present in real systems, therefore they are useful for designing controllers for real applications. In this way, the models' applicability to control design has been verified by means of detailed circuital simulations and experimental results. Moreover, the proposed models are also useful in stability analysis and state observer design to avoid current sensing in MPPT applications.
ACKNOWLEDGMENTS
This work was supported by the GAUNAL group of the Universidad Nacional de Colombia under the project SMART-ALEN.
REFERENCES
[1] Femia,N., Petrone,G., Spagnuolo, G. and Vitelli, M., Optimization of perturb and observe maximum power point tracking method, IEEE Transactions on Power Electronics, vol. 20, pp. 963-973, 2005.
[2] Daoud, A. and Midoun, A., Simulation and Experimental Study of Maximum Power Point Tracker Based on a DC/DC Buck Converter, International Review of Electrical Engineering, vol. 5, pp. 514-520, 2010.
[3] Femia,N., Petrone,G., Spagnuolo,G. and Vitelli, M., A technique for improving P&O MPPT performances of double-stage grid-connected photovoltaic systems, IEEE Transactions on Industrial Electronics, Vol. 56, pp. 4473-4482, 2009.
[4] Femia, N., Lisi,G., Petrone,G., Spagnuolo, G. and Vitelli, M., Distributed Maximum Power Point Tracking of Photovoltaic Arrays: Novel Approach and System Analysis, IEEE Transactions on Industrial Electronics, Vol. 55, pp. 2610-2621, 2008.
[5] Ramos-Paja, C. A., Arango,E., Giral, R., Saavedra-Montes, A. J. and Carrejo, C., DC/DC pre-regulator for input current ripple reduction and efficiency improvement, Electric Power Systems Research, Vol. 81, pp. 2048-2055, 2011.
[6] Arango, E., Ramos-Paja, C. A. and Saavedra-Montes, A. J., Design of asymmetrical boost converters based on photovoltaic systems requirements, DYNA, Vol. 79, No. 171, pp. 31-40, 2012.
[7] Kang, F.-s., Park, S.-J., Cho, S. E. and Kim, J-M., Photovoltaic power interface circuit incorporated with a buck-boost converter and a full-bridge inverter, Applied Energy, Vol. 82, pp. 266-283, 2005.
[8] National-Semiconductor, Solar Magic, http://solarmagic.com, 2011.
[9] Erickson, R. W. and Maksimovic, D., Fundamentals of Power Electronics, 2nd ed. Colorado: Springer, 2001.
[10] BP-Solar, BP585 PV panel datasheet, http://www.oksolar.com/pdfiles/Solar Panels bp_585.pdf, 2011.
[11] Petrone, G. and Ramos-Paja, C. A., Modeling of photovoltaic fields in mismatched conditions for energy yield evaluations, Electric Power Systems Research, Vol. 81, pp. 1003-1013, 2011.
[12] Arango, E., Ramos-Paja, C. A., Gonzalez, D., Serna, S. and Petrone, G., Automatic parameters calculation of controllers for photovoltaic dc/dc converters, Lecture Notes in Electrical Engineering, Vol. 98, pp. 431-44, 2011.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2012 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.




















