SCORE TEST PARA EL EFECTO DEL COEFICIENTE DE SOLAPAMIENTO EN MODELOS DE SUPERFICIES DE RESPUESTA DE PRIMER Y SEGUNDO ORDEN
Palabras clave:
Solapamiento, Superficie de Respuesta, Operador de proyección perpendicular, Score Test. (es)SCORE TEST PARA EL EFECTO DEL COEFICIENTE DE SOLAPAMIENTO EN MODELOS DE SUPERFICIES DE RESPUESTA DE PRIMER Y SEGUNDO ORDEN
SCORE TEST FOR THE OVERLAP COEFFICIENTE EFFECT ON FIRST AND SECOND ORDER RESPONSE SURFACES MODELS
DARGHAN
ENRIQUE
Candidato
a doctor en estadística en la Universidad de los Andes, Mérida. MSc en
estadística Aplicada, e_darghan@unet.edu.ve
SINHA SURENDRA
Coordinador
del Doctorado de Estadística en la Universidad de los Andes, Mérida. PhD en
estadística, sinha@ula.ve
GOITIA ARNALDO
Director
del Instituto de Estadística Aplicada y Computación (IEAC) en
la Universidad de los Andes, Mérida. PhD en estadística
Recibido para revisar septiembre 15 de 2009, aceptado marzo 19 de 2010, versión final mayo 6 de 2010
RESUMEN: En este artículo ha sido propuesto un test para el coeficiente de solapamiento para el modelo de Draper y Guttman utilizando modelos de superficies de respuesta de primer y segundo orden. El test está basado en el test de score de Rao y hace uso de la teoría de operadores de proyección perpendicular. El test puede utilizarse en diferentes patrones de vecindad siempre y cuando se considere al vecino más cercano como la unidad experimental directamente afectada por los tratamientos y los modelos de la superficie sean de primero y segundo orden. El método es simple de adoptar y puede implementarse en el campo de la agronomía o en la investigación de mercados, pues su naturaleza asintótica está en concordancia con el gran número de unidades experimentales generalmente presentes en este tipo de investigaciones.
PALABRAS CLAVE: Solapamiento, Superficie de Respuesta, Operador de proyección perpendicular, Score Test.
ABSTRACT: In this article, a test has been proposed for the overlap coefficient for Draper and Guttman´s model using response surface models of first and second order. The test is based on the Score test of Rao and makes use of the theory of perpendicular projection operators. The test may be used in different neighborhood patterns whenever the closest neighbor can be considered as the experimental unit directly affected by the treatments and the response surface models be of first and second order. The method is simple to adopt and can be implemented in the field of Agronomy or marketing research since it's asymptotic nature is in agreement with the large number of experimental units generally present in this type of researches.
KEYWORDS: Overlap, response surface, perpendicular projection operator , Score Test.
1. INTRODUCCIÓN
En muchos experimentos agropecuarios la aplicación de un tratamiento sobre una unidad experimental pudiera afectar algunas veces la respuesta en las unidades experimentales vecinas, es decir, se presentará un solapamiento mutuo en el uso de los recursos o tratamientos. Los tratamientos aplicados a los cultivos tales como planes de fertilización, riego, aplicación de pesticidas, utilización de controladores biológicos o el uso de agentes inoculantes pudieran dispersarse a las unidades experimentales adyacentes y por ende afectar la(s) variable(s) respuesta que está(n) siendo medida(s). Este fenómeno de solapamiento de tratamientos es muy frecuente y bastaría con visitar alguna una de producción donde se lleven a cabo algunos ensayos para detectar visualmente como parte de uno o varios tratamientos aplicados en una parcela específica terminan en una parcela adyacente, ya sea por agentes climáticos como el viento o simplemente por las labores culturales que se ejercen entre las hileras del cultivo, tal como la eliminación de plantas arvenses. Algunos autores como Bhalli et al (1964) y Hide y Read (1990) describen esta situación en dos cultivos diferentes.
El solapamiento no es un concepto que pueda restringirse a las investigaciones de naturaleza agronómica o biológica en general, pues ya son varias las investigaciones de naturaleza académica que señalan el problema aunque no lo cuantifican. En estudios sobre métodos de enseñanza (clase presencial, semi-presencial, a distancia), donde los alumnos son las unidades experimentales y los tratamientos son los métodos junto con los recursos que usa el docente, pudiera ocurrir solapamiento cuando entre estudiantes se filtra información sobre el método en particular usado por un grupo de ellos. Este solapamiento es similar al descrito por Silk, (1966) y Sudman (1971), quienes atribuyen el solapamiento al flujo de la comunicación entre individuos por medio de los "líderes".
El fenómeno de solapamiento o traslapo ha sido modelado por varios investigadores, entre ellos, Pearce (1957), quien consideró un modelo donde cada tratamiento tiene un efecto directo en la parcela en la cual es aplicado y un efecto de traslapo sobre las parcelas vecinas. Similarmente, Draper y Guttman (1980) estudiaron el solapamiento en superficies de respuesta , específicamente cuando se considera al vecino más próximo (horizontal, vertical o diagonal) como la fuente del traslapo , además, discutieron algunos métodos de prueba aproximados y el intervalo de confianza para el efecto de solapamiento usando el modelo no lineal
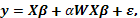 (1)
(1)
donde 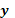 es un vector aleatorio de dimensión
es un vector aleatorio de dimensión  que denota la respuesta de
que denota la respuesta de  unidades experimentales,
unidades experimentales,  es una matriz de diseño
conocida de dimensión
es una matriz de diseño
conocida de dimensión  ,
,  es un vector de parámetros desconocidos de
dimensión
es un vector de parámetros desconocidos de
dimensión  que consiste de los efectos
principales en el caso del modelo de primer orden, y de los efectos
principales, cuadráticos puros y cuadráticos mixtos en el caso del modelo de
segundo orden,
que consiste de los efectos
principales en el caso del modelo de primer orden, y de los efectos
principales, cuadráticos puros y cuadráticos mixtos en el caso del modelo de
segundo orden, 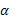 es el efecto desconocido del
traslapo,
es el efecto desconocido del
traslapo,  es una matriz de pesos conocida de dimensión
es una matriz de pesos conocida de dimensión  , donde
, donde 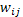 denota el efecto de la unidad j sobre
la unidad i;
denota el efecto de la unidad j sobre
la unidad i;  ;
; 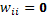 ,
, 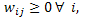 j; finalmente, se asume
para el vector de errores
j; finalmente, se asume
para el vector de errores  que su distribución es normal e independiente
con esperanza cero (E(
que su distribución es normal e independiente
con esperanza cero (E(  )=0) y varianza
)=0) y varianza 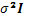 . (Shukla y Subrahmanyan,
1999).
. (Shukla y Subrahmanyan,
1999).
La naturaleza general de 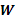 permite a los investigadores
asignar pesos apropiados de consideraciones a priori sobre patrones de
siembra sobre la base del supuesto de que solo el vecino más cercano afecta la unidad con igual intensidad.
permite a los investigadores
asignar pesos apropiados de consideraciones a priori sobre patrones de
siembra sobre la base del supuesto de que solo el vecino más cercano afecta la unidad con igual intensidad.
En la sección 2 de este artículo se describen aspectos teóricos de la metodología de superficies de respuesta y se detallan las matrices de diseño de un modelo de primer orden y uno de segundo orden en particular, ya que su conocimiento será útil para probar solapamiento en el modelo de Draper y Guttman. En la sección 3 se describe el test score de Rao (RST) como una herramienta estadística estándar para llevar a cabo pruebas de hipótesis estadísticas. En la sección 4 se construye el RST para el coeficiente de solapamiento del modelo (1) y en la sección 5 se muestra su aplicación en un patrón de siembra simple de un cultivo hortícola haciendo uso de una superficie de respuesta de cada tipo, es decir, una de primer y una de segundo orden.
2. DESARROLLO DEL SCORE TEST DE SOLAPAMIENTO
2.1 Superficies de
respuesta
La metodología de superficies de respuesta (MSR)
fue desarrollada por Box y Wilson (1951) y es discutida en una gran variedad de
artículos y libros. El mismo Box pero en (1954) enfatizó las bases de la MSR y la ilustró
claramente en una interesante variedad de aplicaciones. En los años
siguientes, Hunter (1958) entre muchos
otros ampliaron su discusión con la incorporación del estudio de las
condiciones óptimas de operación. En los textos de Cochran y Cox (1957) y de
Box y Hunter (1978) se dedica hasta un capítulo entero al estudio de la MSR.
En la actualidad, existen muchos otros textos que ya tratan en todo su
contenido la MSR, tal es el caso de Myers y Montgomery (1995) y Khuri y
Cornell (1996).
Una de las etapas del estudio de una superficie
de respuesta involucra la selección del diseño experimental, entre los cuales
son bastante conocidos aquellos que permiten la estimación de los parámetros en
modelos de primer y segundo orden. En el primer tipo encontramos el diseño
factorial  , replicaciones factoriales del diseño
, replicaciones factoriales del diseño  , el diseño simplex, el diseño
de Plackett-Burman entre otros. Del segundo tipo son conocidos el diseño
factorial
, el diseño simplex, el diseño
de Plackett-Burman entre otros. Del segundo tipo son conocidos el diseño
factorial 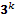 , el diseño de Box-Behnken, el
diseño central compuesto, el diseño equiradial, el diseño rotable
cilíndricamente y el rotable asimétrico,
el diseño saturado de Box-Draper y muchos otros. En ambos tipos encontramos una
discusión detallada en Khuri y Cornell (1996).
, el diseño de Box-Behnken, el
diseño central compuesto, el diseño equiradial, el diseño rotable
cilíndricamente y el rotable asimétrico,
el diseño saturado de Box-Draper y muchos otros. En ambos tipos encontramos una
discusión detallada en Khuri y Cornell (1996).
En esencia, la MSR es un conjunto de técnicas que se aplican antes, mientras y después de realizado un análisis de regresión, aunque antes, el investigador debe haber diseñado el experimento, y una vez hecho el análisis de regresión se ejecutan una serie de pruebas al modelo y se aplican algunas técnicas de optimización, de este modo, la MSR involucra la aplicación de la regresión y otros procedimientos con el fin de ganar mayor entendimiento de las características del sistema de respuestas bajo estudio.
En la MSR suele usarse la estimación
mínimo cuadrática o máximo-verosímil para estimar los coeficientes del modelo
de regresión. Si se asume que el número de observaciones n en la
variable respuesta 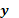 es mayor que el número de
factores involucrados y si el modelo de primer o segundo orden se escribe como
es mayor que el número de
factores involucrados y si el modelo de primer o segundo orden se escribe como 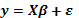 , siendo
, siendo  la matriz de diseño asociada al modelo de
superficie de respuesta y
la matriz de diseño asociada al modelo de
superficie de respuesta y  el vector de errores aleatorios con distribución
normal, independientes y con esperanza
cero (E(
el vector de errores aleatorios con distribución
normal, independientes y con esperanza
cero (E(  )=0) y varianza
)=0) y varianza 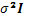 , se tiene entonces que los
parámetros estimados del modelo se estiman mediante
, se tiene entonces que los
parámetros estimados del modelo se estiman mediante
 (2)
(2)
y
 , (3)
, (3)
donde  es la matriz de proyección
perpendicular sobre el espacio de columnas de
es la matriz de proyección
perpendicular sobre el espacio de columnas de  , denotado como
, denotado como  y
y 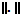 denota la norma usual. La no singularidad de la
matriz
denota la norma usual. La no singularidad de la
matriz 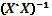 dependerá del diseño, esto implica la
importancia de conocer la estructura de la matriz
dependerá del diseño, esto implica la
importancia de conocer la estructura de la matriz  en su porción factorial, axial y puntos
centrales, pues algunos casos presentan singularidad, por ejemplo, en el diseño
de Box-Behnken, si se tienen
en su porción factorial, axial y puntos
centrales, pues algunos casos presentan singularidad, por ejemplo, en el diseño
de Box-Behnken, si se tienen 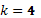 y
y  factores, son necesarios las corridas
centrales para evitar la singularidad de
factores, son necesarios las corridas
centrales para evitar la singularidad de 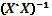 . Montgomery (1995). En todo
caso, aún en presencia de singularidad se podrían imponer condiciones laterales
sobre los parámetros del modelo de modo que pudiera estimarse de forma única
. Montgomery (1995). En todo
caso, aún en presencia de singularidad se podrían imponer condiciones laterales
sobre los parámetros del modelo de modo que pudiera estimarse de forma única 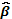 .
.
La similaridad del modelo de Draper y Guttman
bajo la hipótesis nula de "ausencia de solapamiento" con el modelo lineal usual
en la metodología de superficies de respuesta motivó el desarrollo del score
test para el coeficiente de solapamiento en modelos de superficies de respuesta
de primer y segundo orden, ya que la presencia de ciertos puntos de diseño en
estos modelos suelen asegurar la no singularidad de 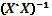 , algo que precisamente
no ocurre en los modelos de clasificación de dos vías, donde es necesario la
imposición de condiciones laterales para la construcción del test (Darghan et
al, 2009). Estos aspectos inducen la presentación teórica de un modelo de
primer orden y posteriormente uno de segundo orden de las siguientes secciones,
con el objeto de entender las características de las matrices de diseño
asociadas y el procedimiento de construcción del test para el coeficiente de
solapamiento basado en la prueba score de Rao.
, algo que precisamente
no ocurre en los modelos de clasificación de dos vías, donde es necesario la
imposición de condiciones laterales para la construcción del test (Darghan et
al, 2009). Estos aspectos inducen la presentación teórica de un modelo de
primer orden y posteriormente uno de segundo orden de las siguientes secciones,
con el objeto de entender las características de las matrices de diseño
asociadas y el procedimiento de construcción del test para el coeficiente de
solapamiento basado en la prueba score de Rao.
2.1.1 El modelo de primer
Orden. Diseño Factorial 
En un diseño factorial  , cada factor es medido a dos
niveles, cuyas combinaciones pueden ser codificados con el par (s,t),
con s=-1,1; t=-1,1, siendo -1 el código asociado al nivel más
bajo del factor y 1 el nivel más alto. Todas las combinaciones de estos niveles
en los
, cada factor es medido a dos
niveles, cuyas combinaciones pueden ser codificados con el par (s,t),
con s=-1,1; t=-1,1, siendo -1 el código asociado al nivel más
bajo del factor y 1 el nivel más alto. Todas las combinaciones de estos niveles
en los  factores rinden la matriz de diseño
factores rinden la matriz de diseño

con  filas, donde la u-ésima fila de
filas, donde la u-ésima fila de  contiene un 1 o un -1, el cual representa la
coordenada del punto de diseño en la u-ésima corrida experimental. En la
matriz
contiene un 1 o un -1, el cual representa la
coordenada del punto de diseño en la u-ésima corrida experimental. En la
matriz  se cumple que
se cumple que 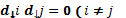 y
y 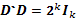 , donde
, donde  denota la matriz identidad de dimensión
denota la matriz identidad de dimensión  .
.
Sin pérdida de la generalidad, si los niveles de los factores se trabajan en variables codificadas, el modelo de primer orden se puede escribir como
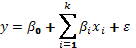 , (4)
, (4)
donde  es una variable respuesta aleatoria
observable,
es una variable respuesta aleatoria
observable,  son los parámetros desconocidos y
son los parámetros desconocidos y 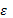 es el término del error aleatorio. (Khuri y
Cornell, 1996).
es el término del error aleatorio. (Khuri y
Cornell, 1996).
El modelo (4) de forma matricial lo escribimos como
 (5)
(5)
el cual es análogo al modelo de solapamiento de
Draper y Guttman, diferenciándose en el término  , el cual considera el coeficiente de
solapamiento
, el cual considera el coeficiente de
solapamiento  y en la naturaleza de la matriz de diseño
y en la naturaleza de la matriz de diseño  , pues en el caso de Draper y
Guttman el modelo es de diseño y en el de una superficie de respuesta el modelo
es de regresión. (Graybill, 1976).
, pues en el caso de Draper y
Guttman el modelo es de diseño y en el de una superficie de respuesta el modelo
es de regresión. (Graybill, 1976).
2.1.2 El modelo de
Segundo Orden. Diseño de Box-Behnken
Box y Behnken (1960) desarrollaron una clase de
diseños a tres niveles para ajustar superficies de respuesta de segundo orden,
la cual se basa en la construcción de diseños en bloques incompletos
balanceados, por ejemplo, en el caso de k tratamientos apareciendo solo
dos en cada bloque, son necesarios k(k-1)/2 bloques para el
balanceo del diseño, cada tratamiento aparece (k-1) veces en el diseño
(Box y Behnken, 1960). El procedimiento se ilustrará en un caso con k=3
factores 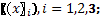 denotando con asteriscos cada
tratamiento, de este modo se obtiene el diseño
denotando con asteriscos cada
tratamiento, de este modo se obtiene el diseño
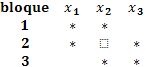
el cual se combina con el procedimiento de un diseño en bloques incompletos balanceado con el diseño factorial 22 usando la estructura

para sustituir cada uno de los asteriscos dentro de
cada bloque con 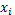 y
y 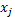 y con ceros donde no aparezca el asterisco. Este
diseño se aumenta con la incorporación de puntos centrales, de modo que la
matriz de diseño resultante tiene la forma
y con ceros donde no aparezca el asterisco. Este
diseño se aumenta con la incorporación de puntos centrales, de modo que la
matriz de diseño resultante tiene la forma
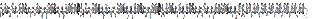 ,
,
donde  ,
, 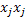 y
y 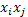 se obtienen de la multiplicación elemento a elemento,
de modo que se generan las estructuras
se obtienen de la multiplicación elemento a elemento,
de modo que se generan las estructuras 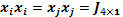 , con
, con  como vector columna de unos;
la estructura
como vector columna de unos;
la estructura  es una nueva estructura factorial útil en la
matriz de diseño ampliada con los efectos cuadráticos puros y mixtos, y
finalmente,
es una nueva estructura factorial útil en la
matriz de diseño ampliada con los efectos cuadráticos puros y mixtos, y
finalmente,  es un vector columna de unos con tantas filas
como puntos centrales (c) se hayan incorporado al diseño, de este modo,
la matriz para usar en el modelo de Draper y Guttman es de la forma.
es un vector columna de unos con tantas filas
como puntos centrales (c) se hayan incorporado al diseño, de este modo,
la matriz para usar en el modelo de Draper y Guttman es de la forma.

de dimensión  , donde n=2k(k-1)+c si se usan dos tratamientos por bloque, y p=(k+1)(k+2)/2, el
cual es el número de columnas de
, donde n=2k(k-1)+c si se usan dos tratamientos por bloque, y p=(k+1)(k+2)/2, el
cual es el número de columnas de  .
.
Es importante recordar que en este diseño se requiere del uso de los puntos centrales, de hecho, para k=4 y k=7 son estrictamente necesarias si se desea evitar la singularidad de la matriz de diseño, por lo que se recomienda el uso de 3 a 5 corridas centrales. (Myers y Montgomery, 1995).
El modelo de segundo orden para el diseño de Box-Behnken y los otros diseños de superficies de respuesta se escriben como en (5) y presenta con el modelo de Draper y Guttman las mismas analogías y diferencias que en el modelo de primer orden, es decir, el término asociado al solapamiento y la naturaleza de la matriz de diseño asociada.
2.2 Score test de
rao
El artículo publicado por Rao (1948) introdujo
un principio fundamental de prueba basado en la función de score como un método
alternativo al de la razón de la verosimilitud y al método de Wald. Varios
autores han descrito las características atractivas del método, entre ellos,
Cramér (1946), Silvey (1959), Chandra
(1985) , Bera (1986) y Bera y Bilias (2001), entre otros.
Sea  la función logaritmo de la verosimilitud de un
vector de parámetros p-dimensional
la función logaritmo de la verosimilitud de un
vector de parámetros p-dimensional  dada una muestra
dada una muestra 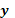 . La función del vector p-dimensional.
. La función del vector p-dimensional.
 (6)
(6)
es conocida como la función de score .
Para un dado  y una variable aleatoria
y una variable aleatoria 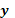 , se tiene que
, se tiene que
 y
y  ,
,
donde  es la matriz de información esperada de
Fisher.
es la matriz de información esperada de
Fisher.
Para probar la hipótesis nula Ho: 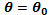 , el estadístico de Rao
viene dado por
, el estadístico de Rao
viene dado por
 , el cual se maximiza en
, el cual se maximiza en
 (7)
(7)
asumiendo que  es definida positiva. Bajo Ho este
estadístico tiene distribución asintótica Chi-cuadrado central con p grados de libertad bajo condiciones generales. (Maddala et al, 1993).
es definida positiva. Bajo Ho este
estadístico tiene distribución asintótica Chi-cuadrado central con p grados de libertad bajo condiciones generales. (Maddala et al, 1993).
2.3 Score test de rao
en el modelo de solapamiento
De ahora en adelante consideraremos el modelo (1),
para el cual asumiremos que  . Suponga que la hipótesis que
deseamos probar es
. Suponga que la hipótesis que
deseamos probar es
H0:  contra Ha:
contra Ha:  , (8)
, (8)
Bajo H0,
el modelo (1) es el modelo lineal usual, expresado como 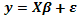 .
.
El logaritmo de la verosimilitud para el modelo (1) es
 , (9)
, (9)
de donde es fácil
calcular el estimador máximo verosímil de  y
y  con
con  , los cuales vienen dados respectivamente por las
expresiones dadas respectivamente en (2) y (3).
, los cuales vienen dados respectivamente por las
expresiones dadas respectivamente en (2) y (3).
Sea  el componente del vector score correspondiente
al parámetro de interés (
el componente del vector score correspondiente
al parámetro de interés (  ) y sea
) y sea

la matriz de
información esperada, particionada de modo que  se corresponda con la segunda derivada parcial
con respecto al parámetro
se corresponda con la segunda derivada parcial
con respecto al parámetro  y
y  se corresponde con las derivadas parciales con
respecto a los parámetros de ruido
se corresponde con las derivadas parciales con
respecto a los parámetros de ruido  . Para construir la prueba se
requiere de la sub-matriz de
. Para construir la prueba se
requiere de la sub-matriz de  correspondiente a
correspondiente a  . El estadístico score para
probar
. El estadístico score para
probar  viene dado por
viene dado por
 (10)
(10)
donde 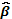 y
y  son los estimadores máximo-verosímiles de
son los estimadores máximo-verosímiles de  respectivamente cuando
respectivamente cuando  y
y  .
.
La función de score asociada al parámetro de interés vine dada por
 , (11)
, (11)
con  el cual al ser evaluado en
el cual al ser evaluado en  se
simplifica a la expresión
se
simplifica a la expresión
 (12)
(12)
sin embargo, por
simplicidad llamaremos  , por lo que (12) se
reduce a
, por lo que (12) se
reduce a
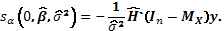 (13)
(13)
A continuación , la
información esperada asociada al parámetro de solapamiento  viene dada por
viene dada por
 , (14)
, (14)
y nuevamente evaluando en  y agrupando términos se tiene que el componente
asociado al parámetro de interés en la inversa de la matriz de información
esperada completa (la que involucra al parámetro de interés como los parámetros
de ruido), es
decir
y agrupando términos se tiene que el componente
asociado al parámetro de interés en la inversa de la matriz de información
esperada completa (la que involucra al parámetro de interés como los parámetros
de ruido), es
decir  es entonces
es entonces
 (15)
(15)
con  , siendo
, siendo  el operador de proyección perpendicular sobre
el espacio columna de
el operador de proyección perpendicular sobre
el espacio columna de  e
e  una matriz de identidad de dimensión
una matriz de identidad de dimensión 
Finalmente, el estadístico de prueba para el coeficiente de solapamiento viene dado por
 (16)
(16)
el cual tiene distribución  con
1 grado de libertad, correspondiente a la dimensión del coeficiente de solapamiento en el modelo de Draper y Guttman.
con
1 grado de libertad, correspondiente a la dimensión del coeficiente de solapamiento en el modelo de Draper y Guttman.
3. APLICACIÓN DEL TEST DE SOLAPAMIENTO
3.1 Modelo de primer orden. Diseño factorial  .
.
El ensayo consistió
en la evaluación del rendimiento (peso en una sola cosecha sin cortes,
g/planta) del cultivo de acelga (beta vulgaris) como consecuencia de
tres factores vinculados a la fertilización según el plan de la unidad de
producción (ver agradecimientos). Los factores se etiquetaron según la aplicación en g/planta de: (x1)-fórmula
química 15:15:15 (3.0 y 5.0), (x2)- fórmula química 12:12:17
(3.0 y 5.0) y (x3)- gallinaza (200 y 250). La siembra se hizo
en tres hileras y en distancias entre plantas e hileras iguales para
simplificar la asignación de los pesos, de este modo se tienen vecinos más
cercanos horizontales, verticales y diagonales, con asignación de pesos
respectivos para las esquinas , bordes no esquineros y plantas entre hileras
excluidos los bordes, tal como se ilustra en la figura 1:
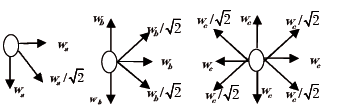
Figura 1. Modelos de
vecindad para el cálculo de los pesos en el patrón de siembra
Figure 1. Neighbourhood
models for the calculation of the weights in the pattern of sowing
Los pesos correspondientes a los diagramas se obtienen de:
(a) 
(b) 
(c) 
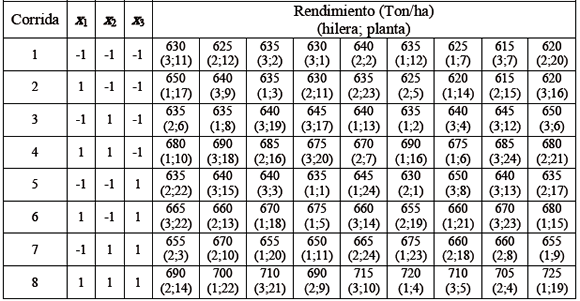
La tabla 1 muestra la disposición de los puntos del diseño en nueve replicas y los datos recolectados en campo en todas las corridas junto con la posición de la planta dentro de cada hilera, ya que de esto dependerá la construcción de la matriz de pesos.
Tabla 1. Disposición del diseño en variables codificadas en nueve réplicas del
diseño 
Table 1. Design layout in codified variables
in nine replicates of  design
design
Los subíndices (s,t,u,r)
del vector de observaciones  cambian más rápido por el lado derecho, es
decir, r=1,2,
,9; u=-1,1; t=-1,1 y s=-1,1.Esto
significa que
cambian más rápido por el lado derecho, es
decir, r=1,2,
,9; u=-1,1; t=-1,1 y s=-1,1.Esto
significa que  representará la observación del nivel s del primer factor (
representará la observación del nivel s del primer factor (  , el nivel t del segundo factor (
, el nivel t del segundo factor (  y el nivel u del tercer factor (
y el nivel u del tercer factor (  en la r-ésima réplica.
en la r-ésima réplica.
El modelo de fila para la
matriz de pesos en la observación  es (
es (  fila 20), el cual pertenece a la hilera
1 y la planta número 8, con vecinos verticales
fila 20), el cual pertenece a la hilera
1 y la planta número 8, con vecinos verticales  , y
, y  , vecino horizontal
, vecino horizontal 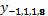 , y vecinos diagonales
, y vecinos diagonales  y
y  . Finalmente la fila queda como:
. Finalmente la fila queda como:

Bajo la hipótesis
nula de ausencia de solapamiento (H0:  ), los parámetros estimados
del modelo son:
), los parámetros estimados
del modelo son:

El score y la
información esperada asociados al parámetro de interés son respectivamente  y
y  , y finalmente, el Score Test de Rao para
solapamiento en el modelo de superficie de respuesta para el diseño
, y finalmente, el Score Test de Rao para
solapamiento en el modelo de superficie de respuesta para el diseño  es
es  , que comparado con la
distribución
, que comparado con la
distribución  con un grado de libertad para un nivel de
confianza del 95%, nos conduce al no rechazo de la hipótesis nula de "no solapamiento", es decir , no existe evidencia estadística para considerar
que existe solapamiento entre la unidades vecinas debido a
las variables de entrada.
con un grado de libertad para un nivel de
confianza del 95%, nos conduce al no rechazo de la hipótesis nula de "no solapamiento", es decir , no existe evidencia estadística para considerar
que existe solapamiento entre la unidades vecinas debido a
las variables de entrada.
3.2 Modelo de
segundo orden. diseño de box-behnken
El experimento consistió en la evaluación del
rendimiento (peso en gramos de cada planta) del cultivo de lechuga (Lactuca sativa L) sometido a 4 factores y 6 bloques. En este ensayo se utilizó un patrón de siembra
por hileras de lechuga, (ver figura 2) . Los tratamientos se etiquetaron como (x1)
a la aplicación de fertilizante en fórmula 12:12:17 (4 y 10 días después del
trasplante) , (x2) a la aplicación de fertilizante en fórmula
15:15:15 (20 y 30 días después del trasplante), (x3) a la
aplicación de estiércol (60 y 100 g/planta) y (x4) aplicación
de urea a nivel foliar(10 y 20 mg/planta).

Figura 2. Modelos de vecindad para el
cálculo de los pesos en el patrón de siembra en bloque 3
Figure 2. Neighbourhood Models for the
calculation of the weights in the pattern of planting in block 3
El punto central (0,0,0,0) está asociado a (7 días, 25 días, 80 g/planta, La disposición de canteros y tratamientos aparecen en la tabla 2, de la cual se observa claramente una corrida central en cada cantero y los dos tratamientos particulares y aleatoriamente asignados en cada bloque.
Tabla 2. Disposición del
diseño en variables codificadas en dos réplicas del diseño
Table 2.Design
layout in codified variables in two replicates of the design
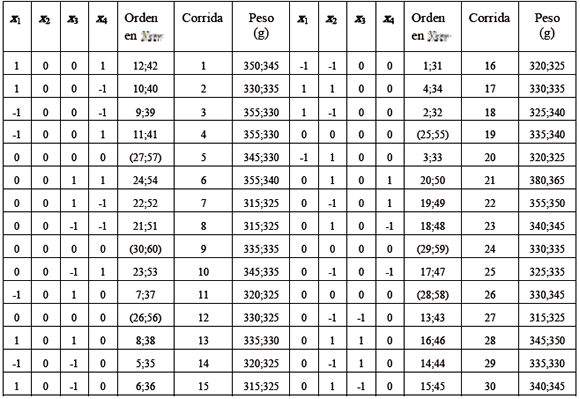
La asignación de pesos para la
construcción de la matriz del patrón de siembra en hileras de la tabla 2 (una
hilera dentro de cada bloque y cada bloque con 5 unidades experimentales) es
fácil de generar, ya que para los bordes se asume que  y entre plantas se asume que
y entre plantas se asume que  y
y  ya que se considera en este
caso que los bloques están lo suficientemente separados como para considerar el
solapamiento entre plantas de canteros diferentes, de ser otro el caso, se
tomarán las plantas entre hileras diferentes en el esquema de vecindad. Las
tres situaciones del caso en estudio se ejemplifican en las figura 2, de donde
las partes (a) y (b) representan las esquinas y la parte (c) representa a las
unidades experimentales no esquineras.
ya que se considera en este
caso que los bloques están lo suficientemente separados como para considerar el
solapamiento entre plantas de canteros diferentes, de ser otro el caso, se
tomarán las plantas entre hileras diferentes en el esquema de vecindad. Las
tres situaciones del caso en estudio se ejemplifican en las figura 2, de donde
las partes (a) y (b) representan las esquinas y la parte (c) representa a las
unidades experimentales no esquineras.
El vector de observaciones 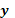 fue llenado respetando la estructura general de
la matriz de diseño, es decir,
fue llenado respetando la estructura general de
la matriz de diseño, es decir,  representa la observación del nivel s del primer factor (
representa la observación del nivel s del primer factor ( 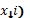 y el nivel t del segundo factor (
y el nivel t del segundo factor (  en el mismo bloque en la réplica r, con s=-1,1; t=-1,1, r=1,2,
,m , teniendo en cuenta que los
factores
en el mismo bloque en la réplica r, con s=-1,1; t=-1,1, r=1,2,
,m , teniendo en cuenta que los
factores 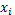 y
y 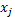 se van considerando según los subíndices
respectivos i=1,2,
,k-1 ; j=1,2,
,k , cambiando más rápido
por el subíndice derecho, lo cual también aplica en el par (s,t),
con lo cual se cubre la porción factorial del diseño, de modo que la parte
final del vector de respuestas se corresponde con la porción asociada a los
puntos centrales. Lo anterior es de mucha importancia ya que la construcción de
la matriz de pesos depende este orden en particular.
se van considerando según los subíndices
respectivos i=1,2,
,k-1 ; j=1,2,
,k , cambiando más rápido
por el subíndice derecho, lo cual también aplica en el par (s,t),
con lo cual se cubre la porción factorial del diseño, de modo que la parte
final del vector de respuestas se corresponde con la porción asociada a los
puntos centrales. Lo anterior es de mucha importancia ya que la construcción de
la matriz de pesos depende este orden en particular.
A
continuación se explicará la construcción de la última fila de la porción
factorial de W (primera réplica), la cual en
este es de dimensión (  , ya que el diseño genera 30 corridas por
réplica. Del vector de respuestas
, ya que el diseño genera 30 corridas por
réplica. Del vector de respuestas  , la fila 5 se corresponde con
los factores
, la fila 5 se corresponde con
los factores  y
y  en sus niveles
bajos (s,t)=(-1,-1), la cual en la tabla 2 se corresponde
con la corrida 14 y en este caso se tiene como vecinos más cercanos a las
corridas 13 y 15, correspondientes a los posiciones 8 y 6 respectivamente en el
vector de respuestas
en sus niveles
bajos (s,t)=(-1,-1), la cual en la tabla 2 se corresponde
con la corrida 14 y en este caso se tiene como vecinos más cercanos a las
corridas 13 y 15, correspondientes a los posiciones 8 y 6 respectivamente en el
vector de respuestas 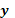 , por lo cual, en la matriz W se asigna el peso de 0.5 en cada una de estas observaciones, quedando la fila 5 como:
, por lo cual, en la matriz W se asigna el peso de 0.5 en cada una de estas observaciones, quedando la fila 5 como:
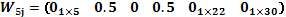
De manera
similar se procede con el resto de filas de la porción factorial hayan o no
réplicas en el diseño, solo que debe tenerse en cuenta que la estructura de 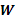 es diagonal por bloques cuando existe más de
una réplica. Finalmente, se asignan los pesos a las filas de los puntos
centrales en cada réplica sin dar importancia al orden en que se haga.
es diagonal por bloques cuando existe más de
una réplica. Finalmente, se asignan los pesos a las filas de los puntos
centrales en cada réplica sin dar importancia al orden en que se haga.
Bajo la hipótesis nula de
ausencia de solapamiento (H0:  ), el vector de parámetros
estimados del modelo, es decir,
), el vector de parámetros
estimados del modelo, es decir, 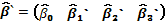 , tiene como componentes a
, tiene como componentes a
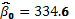 ,
, 

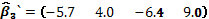 y
y 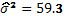 .
.
El score
y la información esperada asociados al parámetro de interés son respectivamente  y
y 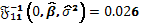 , y finalmente, el RST para
solapamiento en el modelo de superficie de respuesta de Box-Behnken con 4 factores y 6 puntos centrales es
, y finalmente, el RST para
solapamiento en el modelo de superficie de respuesta de Box-Behnken con 4 factores y 6 puntos centrales es 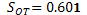 , que comparado con la
distribución
, que comparado con la
distribución  con un grado de libertad, nos conduce al no
rechazo de la hipótesis nula de "no solapamiento", es decir, no existe
evidencia estadística significativa para considerar que existe solapamiento
entre la unidades vecinas debida a los tratamientos.
con un grado de libertad, nos conduce al no
rechazo de la hipótesis nula de "no solapamiento", es decir, no existe
evidencia estadística significativa para considerar que existe solapamiento
entre la unidades vecinas debida a los tratamientos.
4. CONCLUSIONES
Se ha propuesto una prueba estadística para el solapamiento de tratamientos utilizando el modelo de Draper y Guttman con la variante en la matriz de diseño, donde en este caso se usa una matriz de diseño asociada a los modelos de regresión. Este test puede ser aplicado en investigaciones de naturaleza agropecuaria así como también en investigaciones de mercados y académicas, pues el traslapo de tratamientos no es intrínseco a trabajos de origen biológico, sino a cualquier situación en donde parte del tratamiento aplicado sobre una unidad experimental pudiera terminar en la unidad más vecina adyacente (caso espacial común en cultivos) o debido al flujo de información que ocurre entre personas que convergen en un sitio o que simplemente habitan en un nicho particular (caso de las comunidades estudiantiles ). La prueba desarrollada se basa en el test Score de Rao, solo que en este caso hace uso de una teoría muy interesante de los modelos lineales como lo son los operadores de proyección perpendicular en los espacios vectoriales. El test es fácil de adoptar siempre y cuando la estructura del diseño experimental utilizado involucre un modelo como el de Draper y Guttman utilizando como variables de entrada los diferentes factores de una superficie de respuesta de primer o segundo orden y con matrices de diseño definidas positivas. La única dificultad radica en la laboriosa tarea de construir la matriz de pesos, la cual depende del número de puntos diferentes del diseño y del número de réplicas utilizadas en el experimento.
La naturaleza
asintótica del test, es decir, el requerimiento de muestras grandes para
asegurar el comportamiento distribucional del test, induce a la selección de diseños que generen suficientes corridas,
lo cual puede pasar en el diseño factorial  , diseño de Box-Behnken,
diseño factorial
, diseño de Box-Behnken,
diseño factorial  , diseño central compuesto,
entre otros, pero no en los casos como el diseño simplex o el diseño
Plackett-Burman, donde la diferencia entre el número de corridas y el número de
factores es la unidad, de modo que para que la muestra sea grande, sería
preciso trabajar con un gran número de factores, lo cual en la práctica es muy
complicado y costoso.
, diseño central compuesto,
entre otros, pero no en los casos como el diseño simplex o el diseño
Plackett-Burman, donde la diferencia entre el número de corridas y el número de
factores es la unidad, de modo que para que la muestra sea grande, sería
preciso trabajar con un gran número de factores, lo cual en la práctica es muy
complicado y costoso.
Es importante
reconocer la dificultad asociada en la asignación de pesos de la matriz 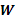 , solo en el ejemplo de
aplicación de Box-Behnhen, fue necesaria una matriz de dimensión
, solo en el ejemplo de
aplicación de Box-Behnhen, fue necesaria una matriz de dimensión  , la cual no es simple para
sistematizar pues la asignación de los tratamientos es totalmente aleatoria y
su conformación depende de cada aleatorización.
, la cual no es simple para
sistematizar pues la asignación de los tratamientos es totalmente aleatoria y
su conformación depende de cada aleatorización.
Finalmente, la
detección de ausencia de solapamiento desde el punto de vista del modelo, asegura como modelo definitivo al modelo
lineal usual, de modo que el proceso de optimización posterior a la
regresión se basará en la superficie de primer o segundo orden postulada, de lo
contrario, sería necesaria una estimación del coeficiente de solapamiento ( 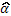 ) y el ajuste de la superficie
) y el ajuste de la superficie  . Además, la ausencia de
solapamiento desde el punto de vista del experimento sugiere una apropiada
aplicación de los tratamientos sobre las unidades experimentales, es decir,
poco o nada de los tratamientos fue a parar en las parcelas vecinas de modo que
este fenómeno afectara el rendimiento. Finalmente, desde el punto de vista de
la superficie de respuesta, una ausencia de solapamiento en un modelo de primer
orden (modelo de ajuste recomendado inicialmente en toda investigación que
requiera el uso de la metodología de superficies de respuesta), propicia el
modelado de segundo orden, en donde seguramente se manejen los tratamientos de
modo similar al modelo de primer orden para garantizar ausencia de solapamiento y probablemente
cambien la región de operación y experimental del ensayo.
. Además, la ausencia de
solapamiento desde el punto de vista del experimento sugiere una apropiada
aplicación de los tratamientos sobre las unidades experimentales, es decir,
poco o nada de los tratamientos fue a parar en las parcelas vecinas de modo que
este fenómeno afectara el rendimiento. Finalmente, desde el punto de vista de
la superficie de respuesta, una ausencia de solapamiento en un modelo de primer
orden (modelo de ajuste recomendado inicialmente en toda investigación que
requiera el uso de la metodología de superficies de respuesta), propicia el
modelado de segundo orden, en donde seguramente se manejen los tratamientos de
modo similar al modelo de primer orden para garantizar ausencia de solapamiento y probablemente
cambien la región de operación y experimental del ensayo.
AGRADECIMIENTOS
Los autores agradecen con vehemencia la colaboración prestada por el Ingeniero y MSc Francisco Bonilla, coordinador de la Unidad Académica "La primavera" adscrita al decanato de extensión de la Universidad Nacional Experimental del Táchira por montar , monitorear y registrar los datos de los experimentos de cada uno de los diseños utilizados como ejemplos de aplicación en este artículo.
REFERENCIAS
[1] BERA, A. K., MCKENZIE, C.R. Alternative forms and properties of the score test. Journal of Applied Statistics. 13, 3-25, 1986.
[2] BERA, A. K. AND BILIAS, Y. Rao´s score, Neyman´s C(a) and Silvey´s LM tests: an essay on historical developments and some new results. Journal of Statistical Planning and Inference 97, 9-44, 2001.
[3] BHALLI, M. A., DAY, A. D., TUCKER, H., THOMSON, R. K., MASSEY, G. D. End-border effects in irrigated barley yield trials. Agronomy Journal, 1964, 346-348, 1964.
[4] BOX, G.E.P. The Exploration and Exploitation of Response Surfaces: Some General Consideration and Examples. Biometrics, Vol. 10, No. 1, pp. 16-60, 1954.
[5] BOX, G.E.P., BEHNKEN, D.W. Some New Three Level Designs for the Study of Quantitative Variables. Technometrics, Vol. 2, No. 4, pp. 455-475, 1960.
[6] BOX, G.E.P., HUNTER, W.G.,HUNTER, J.S. Statistics for Experimenters: An Introduction to Design, Data Analysis, and Model Building , New York : John Wiley, 1978.
[7] BOX, G.E.P., WILSON , K.B. On the Experimental Attainment of Optimum Conditions. Journal of the Royal Statistical Society. Series B (Methodological), Vol. 13, No. 1, pp. 1-45, 1951.
[8] CHANDRA, T. K. AND MUKERJEE, R. Comparison of the likelihood ratio, Wald´s and Rao´s tests. Sankhyã Ser. A 47, 271-284,1985.
[9] COCHRAN, W.G., COX, G.M. Experimental Design. Second edition, New York : John Wiley, 1957.
[10] CRAMÉR, H. Mathematical Methods of Statistics. Princeton University Press, Princeton , N. J., 1946.
[11] DARGHAN, A.E., SINHA, S.P. and GOITIA, A.A. Rao`s Score Test for the Overlap Coefficient in a two way classification model under side conditions. Manuscrito aún no publicado. Proyecto de tesis doctoral. Instituto de Estadística Aplicada y Computación. Universidad de los Andes , Mérida , Venezuela , 2009.
[12] DRAPER, N. R. AND GUTTMAN, J. Incorporating overlap effects from neighbouring units into response surface models. Applied Statistics 39, 128-134, 1980.
[13] GRAYBILL, F.A. Theory and Application of the Linear Model. Wadsworth and Brooks/Cole Advanced Books and Software. A Division of Wadswoth, Inc., 1976.
[14] HIDE, G. A. AND READ, P. J. Effect of neighbouring plants on the yield of potatoes from seed tubers affected with gangrene (Phoma foveata) or from plants affected with stem canker (Rhizoctonia solani). Annals of Applied Biology 116, 233-243, 1990.
[15] HUNTER, J.S. Determination of Optimum Operating Conditions by Experimental Methods: Part II-1. Models and Methods. Industrial Quality Control. Vol. 15, pp. 16-24, 1958.
[16] KHURI, A.I., CORNELL, J.A. Response Surfaces: Design and Analysis. Second edition, Revised and Expanded. Marcel Dekker, Inc.,1996.
[17] MADDALA,G.S., RAO,C.R., VINOD, H.D. Handbook of Statistics. Vol. 11. North Holland , Amsterdam . 800 pp., 1993.
[18] MYERS, R.H., MONTGOMERY , D.C. Response Surface Methodology. Process and Product Optimization Using Designed Experiments. Wiley Series in Probability and Statistics, 1995.
[19] PEARCE, S. C. Experimenting with organisms as blocks. Biometrika 44, 141-149, 1957.
[20] RAO, C. R. Large sample tests of statistical hypothesis concerning several parameters with applications to problems of estimation. Proc. Cambridge Philos. Soc. 44,50-57, 1948.
[21] SHUKLA, G.K., SUBRAHMANYAN, G.S.V. A Note on a test and Confidence Interval for Competition and Overlap Effects. Biometrics, Vol. 55, No. 1, pp. 273-276, 1999.
[22] SILK, A.J. Overlap among Self-Designated Opinion Leaders: A Study of Selected Dental Products and Services. Journal of Marketing Research, Vol. 3, No. 3, pp. 255-259, 1966.
[23] SILVEY, S. D. The Lagrange-multiplier test. Annals of Mathematical Statistics. 30, 389-407, 1959.
[24] SUDMAN, S. Overlap of Opinion Leadership across Consumer Product Categories. Journal of Marketing Research, Vol. 8, No. 2, pp. 258-259, 1971.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2011 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.

















