ANALISIS DE PRIMER y SEGUNDO-ORDEN Y ESTABILIDAD DE PÓRTICOS CON CONEXIONES SEMIRRÍGIDAS: MÉTODO DE HARDY CROSS (I-TEORIA)
Palabras clave:
Análisis estructural, análisis de Segundo-Orden, análisis no-lineal, columnas, conexiones semirrígidas, estabilidad, grandes deformaciones, viga-columnas, vigas. (es)ANALISIS DE PRIMER y SEGUNDO-ORDEN Y ESTABILIDAD DE PÓRTICOS CON CONEXIONES SEMIRRÍGIDAS: MÉTODO DE HARDY CROSS (I-TEORIA)
FIRST- AND SECOND-ORDER ANALYSES AND STABILITY OF FRAMED STRUCTURES WITH SEMIRIGID CONNECTIONS: HARDY CROSS METHOD (I-THEORY)
J. DARIO ARISTIZABAL-OCHOA
Facultad de Minas, Universidad Nacional, Medellín-Colombia, jdaristi@unal.edu.co
Recibido para revisar marzo 19 de 2009, aceptado marzo 20 de 2009, versión final marzo 18 de 2009
RESUMEN: A pesar de que el método de distribución de momentos (MDM) desarrollado por Hardy Cross en 1932 ha sido superado por métodos de cálculo más poderosos como el método de Elementos Finitos este es parte importante de los cursos de análisis y diseño estructural y todavía una herramienta utilizada en la práctica profesional por los ingenieros estructurales. El objetivo principal de esta publicación es presentar una versión extendida del MDM para la estabilidad lateral, el análisis de primer y de segundo-orden de vigas indeterminadas y estructuras aporticadas hechas de vigas y columnas de sección transversal simétrica. Los efectos combinados de las deformaciones por flexión y por cortante, cargas axiales y conexiones semirrígidas son incluidos utilizando la formulación "modificada" de la cortante propuesta por Haringx en 1947 y descrita por Timoshenko y Gere (1961). El método propuesto, el cual incluye los efectos de la componente inducida por la fuerza axial aplicada en la cortante a la lo largo de cada elemento, tiene las siguientes ventajas: 1) puede ser utilizado en el análisis de primer y segundo orden y estabilidad lateral de estructuras aporticadas indeterminadas hechas de vigas y columnas con conexiones rígidas, semirrígidas y simples; 2) los efectos de las conexiones son condensados en los coeficientes de rigidez a flexión y en los momentos fijos sin introducir grados de libertad ni ecuaciones de equilibrio adicionales; y 3) el método es exacto, poderoso, práctico, versátil y es una herramienta excelente de enseñanza. Estudios analíticos indican que los efectos de la cortante, de las conexiones semirrígidas y de la carga axial incrementan las deflexiones laterales y afectan los momentos internos y las reacciones en estructuras aporticadas. Estos efectos deben tenerse en cuenta particularmente en estructuras esbeltas y cuando son hechas de vigas o columnas con área a cortante relativamente pequeña (en celosía) con rigidez a cortante GAs del mismo orden de magnitud que la rigidez a flexión EI/L2 (situación que ocurre en columnas cortas hechas de materiales laminados compuestos con un modulo a cortante G mucho menor que el de elasticidad E). Estos efectos llegan a ser incluso más importantes cuando los apoyos externos no son perfectamente empotrados. Tres ejemplos son incluidos en un artículo adjunto, los cuales muestran la efectividad del método propuesto.
PALABRAS CLAVE: Análisis estructural; análisis de Segundo-Orden; análisis no-lineal; columnas; conexiones semirrígidas; estabilidad; grandes deformaciones; viga-columnas; vigas.
ABSTRACT: A new version of the moment distribution method for both first- and second-order analyses of indeterminate beams and framed structures made of beam-columns of symmetrical cross section including the combined effects of shear and bending deformations, axial loads, and semirigid connections is developed in a classical manner. The proposed method which also includes the effects of the shear component of the applied axial force proposed by Haringx Model in 1947 and described por Timoshenko & Gere (1961) has the following advantages: 1) it can be utilized in the first-and second-order analyses of indeterminate beams and framed structures made of beam-columns with rigid, semirigid, and simple end connections; 2) the effects of semirigid connections are condensed into the bending stiffness and fixed-end moments without introducing additional degrees of freedom and equations of equilibrium; and 3) it is accurate, powerful, practical, versatile, and easy to apply. Analytical studies indicate that shear deformations, semirigid connections and axial loads increase the lateral deflections and affect the internal moments and reactions of continuous beams and framed structures. These effects must be taken into account particularly in slender structures and when they are made of beam or columns with relatively low effective shear areas (like laced columns, columns with batten plates or with perforated cover plates, and columns with open webs) or with low shear stiffness (like short columns made of laminated composites with low shear modulus G when compared to their elastic modulus E) making the shear stiffness GAs of the same order of magnitude as EI/L2. These effects become even more significant when the external supports are not perfectly clamped. Three comprehensive examples are included in a companion paper that shows the effectiveness of the proposed method.
KEY WORDS: Beams; beam-columns; large deflections; nonlinear analysis; semirigid connections; Second-order analysis; stability; structural analysis
1. INTRODUCCIÓN
El método pendiente-deflexión y el método de Hardy Cross representan los puntos de partida en la evolución y desarrollo del análisis estructural matricial y del método de elementos finitos (ó método rigidez) tal como son conocidos en la actualidad [3].
El método pendiente-deflexión fue primero presentado por Wilson y Maney in 1915 [15] en un Boletín de la Universidad de Illinois en Urbana-Champaign como un método general para el análisis de vigas con nudos rígidos sometidas a cargas transversales. Posteriormente, Hardy Cross en 1932 [10, 14], también de la Universidad de Illinois en Urbana-Champaign, propuso un método numérico para el análisis de pórticos rígidos indeterminados que él mismo denominó "Método de Distribución de Momentos". Ambos métodos, basados en los principios de la mecánica estructural los cuales son parte importante del currículo de la ingeniería civil y de los textos clásicos de análisis estructural, brindan una perspectiva clara y describen racionalmente cómo los momentos y fuerzas internas y las correspondientes deformaciones están Inter-relacionadas unos con otras, conceptos que son esenciales en la ingeniería estructural. Quizás, el gran mérito del método de Hardy Cross es que fue parte vital en el desarrollo de la construcción de edificios (de mediana altura y de rascacielos) y puentes con conexiones rígidas y simples e hizo posible diseños seguros y eficientes desde su primera publicación en 1932 como lo atestiguan Lightfoot [11] y más recientemente Eaton [4].
A pesar de que los métodos de pendiente-deflexión y de Hardy Cross han sido superados por el método de Elementos Finitos, ambos son parte importantes en los cursos de análisis y diseño estructural y son utilizados por una gran cantidad de ingenieros estructurales. En el método de Hardy Cross se supone que los nudos de un pórtico están inicialmente fijos o empotrados contra rotación. Los momentos fijos en los extremos producidos por las cargas externas son calculados primero, al igual que los factores de distribución y de transporte de cada viga y columna del pórtico en cuestión. Los momentos fijos no están balanceados en los nudos de la estructura real. Con el fin de obtener equilibrio rotacional en cada nudo, los momentos fijos en cada nudo son distribuidos a cada miembro proporcionalmente a su rigidez a flexión. Los momentos distribuidos están asociados con los momentos "transportados" al extremo opuesto del elemento estructural. Estos se consideran como los nuevos momentos incrementales no balanceados y el procedimiento se repite hasta que los momentos no balanceados se vuelven despreciables. Finalmente, el momento real en un extremo de un elemento es la suma de todos los incrementos de los momentos no balanceados. Inicialmente, el método de Cross supone únicamente rotaciones en los nodos. Sin embargo, en pórticos con traslación en los nodos un esquema más general es utilizado, el cual requiere la aplicación del método sucesivamente, asignando un sistema de ecuaciones donde la traslación de los nodos (o derivas) son desconocidas.
Por otra parte, avances en materiales compuestos de alta capacidad elástica (resilientes) y de baja rigidez a la cortante, al igual que la necesidad de vigas y columnas mas livianas y mas esbeltas, han creado un gran interés en los efectos de la cortante y en el análisis de segundo-orden de estructuras aporticadas. Las ecuaciones de pendiente-deflexión para la viga de Timoshenko incluyendo los efectos de la deformación por cortante y cargas transversales fueron desarrolladas por Bryan y Baile [8]. Anteriormente, Lin, Glauser y Johnson [13] desarrollaron las ecuaciones de pendiente deflexión para viga-columnas de alma abierta incluyendo los efectos de la deformaron por cortante, carga axial, y platinas rígidas. Las ecuaciones de pendiente deflexión para la viga de Timoshenko incluyendo los efectos de la deformación por cortante y por flexión, efectos de segundo orden y conexiones semirrígidas en los extremos han sido presentadas por Aristizabal-Ochoa [1, 2] utilizando funciones de estabilidad.
El objetivo principal de esta publicación es presentar una nueva versión del método clásico de distribución de momentos para el análisis de primer y de segundo orden (incluyendo estabilidad) de estructuras aporticadas hechas de vigas y columnas de sección transversal simétrica incluyendo los efectos de: 1) la deformación por cortante y por flexión; 2) la componente de la cortante en la fuerza axial aplicada (modelo de Haringx); y 3) conexiones semirrígidas en los extremos de cada elemento. El método propuesto, el cual está basado en las ecuaciones "modificadas" de estabilidad para la columna de Timoshenko con conexiones semirrígidas desarrollas por el autor [1,2], tiene las siguientes ventajas: 1) los efectos de las conexiones semirrígidas están condensados en el método sin introducir grados de libertad adicionales; 2) es capaz de capturar no sólo el pandeo por divergencia bajo fuerzas de compresión, sino también el fenómeno de pandeo de columnas y pórticos sometidos a fuerza axial de tracción; y 3) es exacto, poderoso, práctico, versátil y fácil de enseñar. Son incluidos tres ejemplos que muestran con detalles la efectividad del método propuesto y las ecuaciones correspondientes.
2. MODELO ESTRUCTURAL
2.1 Suposiciones
Consideremos una viga-columna que conecta los puntos J y K como es mostrado en la Figura 1a. El elemento está compuesto de la viga-columna J’K’ como tal, y las conexiones a flexión JJ’ y KK’ con rigidez a flexión  en los extremos J y K, respectivamente. Se asume que la viga-columna J’K’ de longitud L se flexiona con respecto al eje principal de su sección transversal cuyo momento de inercia es I, área efectiva a cortante As y: 1) está hecha de material homogéneo elástico lineal con módulos de Young y de cortante E y G respectivamente; 2) su eje centroidal es una línea recta; y 3) está cargada en ambos extremos con P (carga axial) a lo largo de su eje centroidal.
en los extremos J y K, respectivamente. Se asume que la viga-columna J’K’ de longitud L se flexiona con respecto al eje principal de su sección transversal cuyo momento de inercia es I, área efectiva a cortante As y: 1) está hecha de material homogéneo elástico lineal con módulos de Young y de cortante E y G respectivamente; 2) su eje centroidal es una línea recta; y 3) está cargada en ambos extremos con P (carga axial) a lo largo de su eje centroidal.
Las conexiones tienen rigidez a flexión (cuyas unidades son fuerza-distancia/radian) en el plano de flexión de la viga columna. Las relaciones
(cuyas unidades son fuerza-distancia/radian) en el plano de flexión de la viga columna. Las relaciones  son denotadas como los índices de fijeza de las conexiones a flexión. Estos índices varían de cero
son denotadas como los índices de fijeza de las conexiones a flexión. Estos índices varían de cero  para conexiones simples (esto es, articuladas) hasta infinito
para conexiones simples (esto es, articuladas) hasta infinito  para conexiones totalmente restringidas (o rígidas). Nótese que el algoritmo propuesto puede ser utilizado en el análisis inelástico de viga-columnas cuando el comportamiento inelástico es concentrado en las conexiones. Esto puede ser llevado a cabo actualizando la rigidez a flexión de las conexiones
para conexiones totalmente restringidas (o rígidas). Nótese que el algoritmo propuesto puede ser utilizado en el análisis inelástico de viga-columnas cuando el comportamiento inelástico es concentrado en las conexiones. Esto puede ser llevado a cabo actualizando la rigidez a flexión de las conexiones  para cada incremento de carga de la manera incremental.
para cada incremento de carga de la manera incremental.

Figura 1.Viga-Columna bajo momentos en los extremos con conexiones semirrígidas: (a) Modelo estructural; (b) Grados de libertad, fuerzas y momentos en el planos de la flexión; (c) Rotaciones en una sección transversal y en los extremos A y B.
Figure 1. Beam-Column under end moments with semi-rigid connections: (a) Structural Model; (b) Degrees of Freedom, Forces and Moments in the plane of bending; (c) Rotations at a cross section and at ends J and K.
Por conveniencia los siguientes parámetros son introducidos:
 ; y
; y 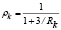 (1a-b)
(1a-b)
 son llamados factores de fijeza. Para conexiones articuladas, tanto el factor de fijeza
son llamados factores de fijeza. Para conexiones articuladas, tanto el factor de fijeza  como el índice de rigidez R son cero; pero para conexiones rígidas, el factor de fijeza es uno y el índice de rigidez es infinito. Debido a que el factor de fijeza varía entre 0 y 1 para conexiones elásticas (mientras que el índice de rigidez R puede variar desde 0 a
como el índice de rigidez R son cero; pero para conexiones rígidas, el factor de fijeza es uno y el índice de rigidez es infinito. Debido a que el factor de fijeza varía entre 0 y 1 para conexiones elásticas (mientras que el índice de rigidez R puede variar desde 0 a  ), es más conveniente usarlo en el análisis elástico de estructuras con conexiones semirrígidas.
), es más conveniente usarlo en el análisis elástico de estructuras con conexiones semirrígidas.
3. ECUACIONES PROPUESTAS
Con el fin de investigar el análisis de primer y de segundo orden de vigas indeterminadas y estructuras aporticadas con conexiones semirrígidas, es necesario primero establecer las relaciones entre los momentos flectores en el extremo y las correspondientes rotaciones para cada elemento del pórtico y luego aplicar las condiciones de compatibilidad de deformaciones en cada nodo. La aplicación del método clásico de la distribución de momentos en el análisis estático de vigas y pórticos planos (con conexiones rígidas y carga transversal a lo largo del elemento) es bien explicado en los libros del análisis estructural como los de Kassimali [7] y Norris y Wilbur [9], entre otros. Las ecuaciones propuestas pendiente-deflexión para pórticos planos con conexiones semirrígidas incluyendo la deformación por cortante y los efectos de segundo-orden (efectos  ) a lo largo de elemento son como siguen:
) a lo largo de elemento son como siguen:
 (2a)
(2a)
 (2b)
(2b)
Como muestra la figura 1c, 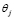 y
y 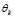 son las rotaciones de los extremos J y K medidas con respecto al eje inicial del elemento, y
son las rotaciones de los extremos J y K medidas con respecto al eje inicial del elemento, y  /L el ángulo de rotación de la cuerda del elemento JK. Todas las rotaciones (
/L el ángulo de rotación de la cuerda del elemento JK. Todas las rotaciones (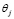 ,
,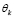 y
y  /L), los momentos en los extremos (Mj y Mk) y los momentos fijos en los extremos (FEMj y FEMk) son positivos en el sentido de las agujas del reloj. Nótese que los coeficientes de rigidez de una viga-columna de Timoshenko con conexiones semirrígidas en los extremos J y K son denotados como Sjj, Sjk, Skj y Skk. Estos coeficientes y los momentos fijos en los extremos se presentan a continuación para su fácil referencia.
/L), los momentos en los extremos (Mj y Mk) y los momentos fijos en los extremos (FEMj y FEMk) son positivos en el sentido de las agujas del reloj. Nótese que los coeficientes de rigidez de una viga-columna de Timoshenko con conexiones semirrígidas en los extremos J y K son denotados como Sjj, Sjk, Skj y Skk. Estos coeficientes y los momentos fijos en los extremos se presentan a continuación para su fácil referencia.
Coeficientes de Rigidez de Primer orden
Para P= 0
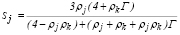 (3)
(3)
 (4)
(4)
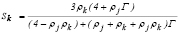 (5)
(5)
Coeficientes de Rigidez de Segundo-Orden
Para P > 0 (compresión) o 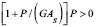
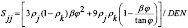 (6)
(6)
 (7)
(7)
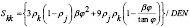 (8)
(8)
Donde: 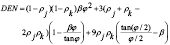
b) Para P<0 (tracción) o 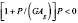
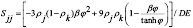 (9)
(9)
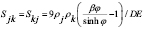 (10)
(10)
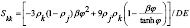 (11)
(11)
Donde: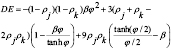
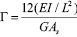 ;
;
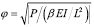 ; y
; y

Momentos fijos en los extremos FEMj y FEMk y factores de transporte COFjk y COFkj
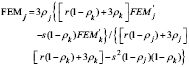 (12)
(12)
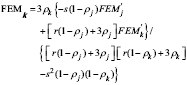 (13)
(13)
 y
y 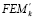 son los momentos fijos en los extremos cuando el elemento está perfecta-mente empotrado en los dos extremos (esto es,
son los momentos fijos en los extremos cuando el elemento está perfecta-mente empotrado en los dos extremos (esto es,  1). Estos momentos están en las tablas 1-2 para los cuatro casos de carga diferentes que se muestran en la figura 2. De manera similar, las expresiones para r y s son idénticas a los coeficientes Sjj y Sjk de una viga-columna con los extremos perfectamente empotrados (
1). Estos momentos están en las tablas 1-2 para los cuatro casos de carga diferentes que se muestran en la figura 2. De manera similar, las expresiones para r y s son idénticas a los coeficientes Sjj y Sjk de una viga-columna con los extremos perfectamente empotrados ( 1), respectivamente.
1), respectivamente.
Tabla 1. Expresiones de primer orden para r, s, 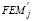 y
y 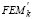 (P= 0)
(P= 0)
Table 1. First-order expressions for r, s, 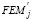 y
y 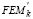 (P= 0)
(P= 0)

Tabla 2. Expresiones de segundo orden para r, s,  y
y 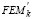 [para
[para  (Compresión) o
(Compresión) o  ]*
]*
Table 2. Second order expressions for r, s, 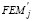 y
y 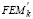 [for
[for  (Compression) or
(Compression) or ]*.
]*.


Figura 2. Casos de carga: (a) Carga concentrada W; (b) Momento M; (c) Carga parcial uniformemente distribuida w; (d) Carga parcial linealmente distribuida w.
Figure 2. Load cases: (a) Concentrated Load W; (b) Moment M; (c) Uniformly Distributed Partial Load w; (d) Linearly Distributed Partial Load w.
*Para P< 0 (tracción) y 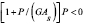 (esto es, cuando
(esto es, cuando 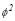 es negativo) los siguientes tres cambios de variable deben ser hechos en todas las expresiones: 1) sen
es negativo) los siguientes tres cambios de variable deben ser hechos en todas las expresiones: 1) sen  por isenh
por isenh  ; 2) tan
; 2) tan  por itanh
por itanh  ; y 3)
; y 3)  por i
por i  (donde: i=
(donde: i=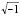 ) 4) cos
) 4) cos  por cosh
por cosh  . Nótese que las expresiones para r y s son idénticas a los coeficientes Sjj y Sjk dados por las ecs. (3) y (4) para una viga-columna con extremos perfectamente empotrados (
. Nótese que las expresiones para r y s son idénticas a los coeficientes Sjj y Sjk dados por las ecs. (3) y (4) para una viga-columna con extremos perfectamente empotrados ( j=
j= k= 1), respectivamente.
k= 1), respectivamente.
Las expresiones para 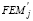 y
y 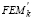 en la tabla 1 fueron deducidas por Bryant y Baile [8] y las presentadas en la tabla 2 fueron desarrolladas por Lin y otros [13]. Los factores de transporte COFjk y COFkj están dados por la relación Sjk/Sjj y Skj/Skk respectivamente. Las ecs. (1)-(11) son deducidas en el Apéndice II. Las ecs. (12)-(13) de los momentos fijos son idénticas a las desarrolladas previamente por el autor [1, 5].
en la tabla 1 fueron deducidas por Bryant y Baile [8] y las presentadas en la tabla 2 fueron desarrolladas por Lin y otros [13]. Los factores de transporte COFjk y COFkj están dados por la relación Sjk/Sjj y Skj/Skk respectivamente. Las ecs. (1)-(11) son deducidas en el Apéndice II. Las ecs. (12)-(13) de los momentos fijos son idénticas a las desarrolladas previamente por el autor [1, 5].
Se presentan tres ejemplos en el artículo adjunto que muestran la efectividad, simplicidad y exactitud del método de distribución de momentos. Los ejemplos 1 y 2 son sobre el análisis de primer y segundo orden de vigas continuas con conexiones semirrígidas sometidas a cargas transversales incluyendo la deformación por cortante. El ejemplo 3 muestra también la aplicación del método propuesto en el análisis de primer y segundo orden de un pórtico plano irregular con conexiones semirrígidas.
4. RESUMEN Y CONCLUSIONES
Una nueva versión del método de distribución de momentos para análisis de primer y de segundo orden de vigas indeterminadas y estructuras aporticadas hechas de viga-columnas de sección transversal simétrica, incluyendo los efectos de la deformación por cortante y por flexión, los efectos de la carga axial y conexiones semirrígidas es desarrollado de la manera clásica.
Esta nueva versión, la cual se basa en las funciones de estabilidad "modificadas" para viga-columnas con conexiones semirrígidas desarrolladas por Aristizábal-Ochoa [1, 2, 5] incluyendo los efectos de la componente en la cortante de la carga axial aplicada (Modelo de Haringx) tiene las siguientes ventajas: 1) puede ser utilizado en el análisis de primer y segundo orden al igual que en el análisis de estabilidad de estructuras aporticadas indeterminadas; 2) los efectos de las conexiones semirrígidas están condensados en la rigidez a flexión y en los momentos fijos sin introducir grados de libertad adicionales; 3) es capaz de capturar no sólo el pandeo bajo fuerzas de compresión sino también el fenómeno de pandeo de columnas y pórticos sometidos a fuerzas axiales de tracción; y 4) es exacto, poderoso, versátil y relativamente fácil de aplicar.
Estudios analíticos indican que la deformación por cortante, la fuerza axial de compresión, y las conexiones semirrígidas incrementan la deflexión lateral y afecta los momentos y reacciones internas de vigas continuas indeterminadas y estructuras aporticadas. Los efectos de la cortante deben de ser considerados en el análisis de estructuras hechas de vigas-columnas de alma abierta con área efectiva a cortante relativamente baja o poca rigidez a cortante (columnas cortas hechas de materiales compuestos laminados con bajo modulo de cortante G cuando es comparado con su modulo de elasticidad E, haciendo la rigidez a cortante GAs del mismo orden de magnitud de EI/L2). La deformación por cortante es particularmente importante cuando los apoyos no están perfectamente empotrados y las condiciones de carga no son simétricas. La validez y efectividad de las ecuaciones propuestas son verificadas con soluciones bien documentadas sobre la estabilidad estática y el análisis de primer y según-do orden de vigas columnas y pórticos planos.
5. AGRADECIMIENTOS
Esta investigación fue llevada a cabo en la Universidad Nacional, Facultad de Minas. El autor quiere expresar su apreciación al DIME por el apoyo financiero, a John Monsalve Cano, Jaime Hernández Urrea y Camilo Builes Mejía miembros del Grupo GES por las revisiones hechas a las ecuaciones y su programación por computador.
6. APÉNDICE I
6.1 Deducción de las Ecs. (2a)-(2b) y (6)-(8)
La estabilidad y el análisis de segundo orden de una columna prismática incluyendo la deformación por flexión y por cortante (Figs. 1a-c) es formulada usando el modelo de cortante "modificada" de Haringx en 1947 ([12], pág. 134). Este modelo ha sido utilizado previamente por Aristizábal-Ochoa [9, 10] en el análisis de grandes deformaciones de viga-columnas. Las ecuaciones gobernantes son como se muestran a continuación:
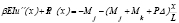 ? (14a)
? (14a)
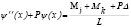 (14b)
(14b)
Donde: u(x)= deflexión lateral de la línea central; y  (x)= rotación de la sección transversal debida únicamente a la flexión como muestran las figuras 1b-c.
(x)= rotación de la sección transversal debida únicamente a la flexión como muestran las figuras 1b-c.
Las soluciones de las ecuaciones diferenciales de segundo orden (14a)-(14b) son:
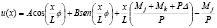 (15a)
(15a)
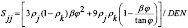 (15b)
(15b)
Los coeficientes desconocidos A, B, C y D pueden ser obtenidos de las siguientes condiciones de borde:
En 
En 
Donde:  = rotación de la sección transversal en los extremos J’ y K’ respecto al eje vertical debido a flexión, respectivamente. Por lo tanto:
= rotación de la sección transversal en los extremos J’ y K’ respecto al eje vertical debido a flexión, respectivamente. Por lo tanto: 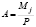 ;
; 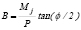 -
- ;
;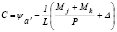 ; y
; y
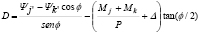
Sabiendo que
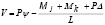

las expresiones para  son:
son:
 (16a)
(16a)
 (16b)
(16b)
Ya que las rotaciones en J y K son:
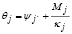 y
y 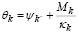
Por lo tanto:
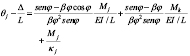 (17a)
(17a)
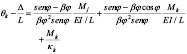 (17b)
(17b)
Donde: = deriva relativa del extreme K con respecto al extremo J;
= deriva relativa del extreme K con respecto al extremo J;  = rotaciones de los extremos J y K debidas a la flexión con respecto al eje vertical, respectivamente.
= rotaciones de los extremos J y K debidas a la flexión con respecto al eje vertical, respectivamente.
Nótese que las ecuaciones (16a) y (16b) son idénticas a las demostradas por Salmon y Johnson ([6], p. 902) para una columnas de Bernoulli-Euler (esto es, cuando  = 1). Ahora, expresando las ecuaciones (17a) y (17b) en forma matricial, y luego invirtiendo la matriz de coeficientes y usando las expresiones (1a) y (1b)
= 1). Ahora, expresando las ecuaciones (17a) y (17b) en forma matricial, y luego invirtiendo la matriz de coeficientes y usando las expresiones (1a) y (1b)  , las ecuaciones (2a) y (2b) pueden ser obtenidas.
, las ecuaciones (2a) y (2b) pueden ser obtenidas.
Para P<0 (tracción) y 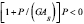 (esto es, cuando
(esto es, cuando 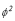 se vuelve negativo) las siguientes tres sustituciones deben ser hechas en las ecuaciones (6)-(8): 1)
se vuelve negativo) las siguientes tres sustituciones deben ser hechas en las ecuaciones (6)-(8): 1)  2)
2) 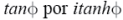 ; y 3)
; y 3)  por i (donde: i=
por i (donde: i=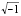 ). Entonces las expresiones (9)-(11) pueden ser obtenidas.
). Entonces las expresiones (9)-(11) pueden ser obtenidas.
6.2 Deducciones de las Ecuaciones (3)-(5)
Las ecuaciones gobernantes (14a) y (14b) cuando P= 0 se reducen a:
 (18a)
(18a)
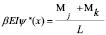 (18b)
(18b)
Las ecs. (18a) y (18b) son ahora mucho más simples de resolver. Después de aplicar las condiciones de borde [esto es,  en K´ (x= L)], sus soluciones son:
en K´ (x= L)], sus soluciones son:
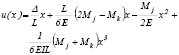 (19a)
(19a)
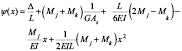 (19b)
(19b)
Sabiendo que  y
y 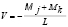 , entonces
, entonces  pueden ser obtenidas de la ecuación (19b):
pueden ser obtenidas de la ecuación (19b):
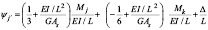 (20a)
(20a)
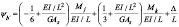 (20b)
(20b)
Como se explicó previamente (ver fig. 1c), las rotaciones en los extremos J y K son
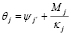 y
y 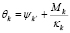 , respectivamente. Por lo tanto:
, respectivamente. Por lo tanto:
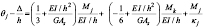 (21a)
(21a)
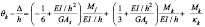 (21b)
(21b)
Expresando las ecuaciones (21a) y (21b) en forma matricial y luego invirtiendo la matriz de coeficientes y usando  , las ecuaciones (2a)-(2b) y (3)-(5) pueden ser obtenidas.
, las ecuaciones (2a)-(2b) y (3)-(5) pueden ser obtenidas.
9. NOTACIÓN
Los siguientes símbolos son usados en este documento:
As= área efectiva de cortante de la sección transversal de la viga-columna;
E = módulo de Young del material;
G= modulo de cortante del material;
L= longitud de la viga-columna AB;
I= momento principal de inercia de la viga-columna alrededor del eje de flexión;
Mj y Mk= momentos flectores en los extremos J y K, respectivamente;
P= carga axial aplicada en J y K(+compresión, -tracción);
 = carga crítica axial;
= carga crítica axial;
Pe =  =carga crítica de Euler;
=carga crítica de Euler;
Rj y Rk= índices de rigidez de las conexiones a flexión en J y K, respectivamente;
u(x)= deflexión lateral de la línea central de la viga-columna
 = factor de reducción del la rigidez a flexión causada por la cortante;
= factor de reducción del la rigidez a flexión causada por la cortante;
 = deriva del extremo B con respecto a A;
= deriva del extremo B con respecto a A;
 = rigidez a flexión de las conexiones en los extremos en J y K, respectivamente;
= rigidez a flexión de las conexiones en los extremos en J y K, respectivamente;
 = factores de fijeza en J y K, respectivamente;
= factores de fijeza en J y K, respectivamente;
 = rotación de la sección transversal debido solamente a flexión como muestra la fig. 1c;
= rotación de la sección transversal debido solamente a flexión como muestra la fig. 1c;
 = rotaciones por flexión de las secciones transversales en los extremos J´ y K´ con respecto a la cuerda J´K´, respectivamente;
= rotaciones por flexión de las secciones transversales en los extremos J´ y K´ con respecto a la cuerda J´K´, respectivamente;
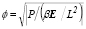 = función de estabilidad en el plano de flexión;
= función de estabilidad en el plano de flexión;
 = rotaciones de los extremos J y K debido a flexión con respecto al eje vertical, respectivamente.
= rotaciones de los extremos J y K debido a flexión con respecto al eje vertical, respectivamente.
 = coeficiente de reducción por cortante.
= coeficiente de reducción por cortante.
REFERENCIAS
[1] ARISTIZABAL-OCHOA, J. DARÍO. Slope-deflection Equations for stability and second-order analysis of Timoshenko beam-column structures with semi-rigid connections, ELSEVIER Journal of Engineering Structures, Vol. 30(9), pp. 2517-2527, 2008.
[2] ARISTIZABAL-OCHOA, J. DARÍO. Large Deflection and Postbuckling Behavior of Timoshenko Beam-Columns with semirigid connections including Shear and Axial Effects, ELSEVIER Journal of Engineering Structures, Vol. 29 (6), 991-1003, 2007.
[3] SAMUELSSON, A. AND ZIENKIEWICZ, O. C. "History of the Stiffness Method," International Journal for Numerical Methods in Engineering, Wiley InterScience, Vol. 67, 149-157, 2006.
[4] EATON, L. K. Hardy Cross and the Moment Distribution Method,Vol. 3 (2) September, Nexus Network Journal, Birkhäuser Basel, 15-24, 2001.
[5] ARISTIZABAL-OCHOA, J. DARIO. First- and second-order stiffness matrices and load vector of beam-columns with semirigid connections, J. Struct. Engrg., ASCE, 123(5), pp. 669-678, 1997.
[6] SALMON, C. G. AND JOHNSON, J.E., Steel Structures: Design and Behavior, 4th Ed., HarperCollins College Publishers (Chapter 14), Michigan, 1996.
[7] KASSIMALI, A., Structural Analysis, PWS-Kent, London, 1993.
[8] BRYANT, R. H. AND BAILE, O. C. Slope Deflection Analysis Including Transverse Shear, J. of the Structural Division, Vol. 103, No. 2, 443-446, 1977.
[9] NORRIS, C.H., WILBUR, J.B., AND UTKU, S., Elementary Structural Analysis, 3rd Ed., McGraw-Hill, New York, 1976.
[10] CROSS, HARDY. Arches, Continuous Frames, Columns, and Conduits: Selected Papers, University of Illinois Press, 265, 1963.
[11] LIGHTFOOT, E. Moment Distribution: a Rapid Method of Analysis for Rigid-Jointed Structures, Wiley & Sons Inc., New York, 1961.
[12] TIMOSHENKO, S. AND GERE, J. Theory of Elastic Stability, 2nd Ed., McGraw-Hill, Chapter II, New York, 1961.
[13] LIN, F. J., GLAUSER E. C., AND JOHNSTON B. J. Behavior of Laced and Battened Structural Members, J. Struct. Engrg., ASCE, 123(5), 1377-1401, 1960.
[14] CROSS, HARDY. Analysis of Continuous Frames by Distributing Fixed-end Movements," University of Illinois Press, 1932.
[15] WILSON, W. M. AND MANEY, G. A. Slope-Deflection Method," University of Illinois Engineering Experiment Station, Bulletin 80, 1915.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2011 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.

















