CONSTITUYENTES DE MAREA EN LA BAHÍA DE SANTA MARTA (COLOMBIA)

Se realizó un análisis de la onda de marea en la bahía de Santa Marta. La onda de marea fue medida mediante la ayuda de un mareógrafo WLR 7 de la familia Aandera. A partir de las series de tiempo obtenidas se determinó la amplitud y la fase de los constituyentes principales de la marea mediante un análisis de armónicos efectuado con la técnica de ajuste de mínimos cuadrados. Se encontró una marea con características mixta principalmente diurna conformada por 12 constituyentes, de ellos seis son de carácter diurno (K1, O1, P1, Q1, J1, OO1) y cinco de carácter semidiurno (M2, S2, K2, N2, Mu2) además de la Componente lunisolar sinódica quincenal (Msf).

TIDE CONSTITUENTS AT SANTA MARTA BAY (COLOMBIA)

FRANCISCO GARCÍA
Universidad del Magdalena, Docente, fcofdogarcia@yahoo.com

CARLOS PALACIO
Universidad de Antioquia, Docente, cpalacio@udea.edu.co

URIEL GARCIA
Universidad del Magdalena, Docente, uriel.garcia@yahoo.es

Recibido para revisar septiembre 9 de 2009, Aceptado diciembre 18 de 2009, versión final abril 10 de 2010

---

RESUMEN: Se realizó un análisis de la onda de marea en la bahía de Santa Marta. La onda de marea fue medida mediante la ayuda de un mareógrafo WLR 7 de la familia Aandera. A partir de las series de tiempo obtenidas se determinó la amplitud y la fase de los constituyentes principales de la marea mediante un análisis de armónicos efectuado con la técnica de ajuste de mínimos cuadrados. Se encontró una marea con características mixta principalmente diurna conformada por 12 constituyentes, de ellos seis son de carácter diurno (K1, O1, P1, Q1, J1, OO1) y cinco de carácter semidiurno (M2, S2, K2, N2, Mu2) además de la Componente lunisolar sinódica quincenal (Msf).

PALABRAS CLAVE: Marea, Análisis de armónicos, mareógrafos

ABSTRACT: A tide analysis in Santa Martha bay was performed. Tide measurements were effectuated at Santa Marta bay using WLR7 Mareograph of Aandera family. The amplitude and phase of principal constituents of the tide were established from the time series using the harmonic analysis with least square technique. The tides are mixed mainly diurnal with 12 main constituents, six diurnal (K1, O1, P1, Q1, J1, OO1), five semi-diurnal (M2, S2, K2, N2, Mu2) and the lunisolar synodic fortnightly tidal constituent (MSf)

KEYWORDS: Tide, Harmonic analysis, Mareograph.

---

1. INTRODUCCIÓN

Las mareas son una herramienta útil para ayudar a despejar las interrogantes sobre la evolución de los ecosistemas costeros [1]. El análisis y predicción de estas, fue uno de los aportes de la física en el siglo XIX. Inspirados por la teoría gravitacional de Newton, la mecánica celeste de Laplace y la metáfora de un perfecto mecanismo de reloj en perpetuo movimiento, los físicos descubrieron como predecir las mareas en un determinado lugar mediante el ajuste de las mediciones del ascenso y descenso del nivel de la superficie del mar a un conjunto de coeficientes de una suma finita de ondas sinusoidales con la precisión conocida de periodos orbitales del sistema luna-tierra-sol [2]. Esta elevación y descenso rítmico del nivel del mar debido a las mareas es el resultado de la fuerza gravitacional del sol y la luna [3]. Según Godín [4] la marea es una modificación temporal en la posición de la materia en una parte de un astro, causado por un cambio de las fuerzas gravitacionales que ejercen sobre ella otros astros y que en el océano se manifiesta como un movimiento regular del nivel del mar. Estas variaciones del nivel del mar son, adicionalmente, afectadas por fenómenos internos y efectos locales. Como el campo gravitacional es conservativo, permite la determinación de los períodos y las amplitudes de las componentes de la fuerza de marea, llamadas constituyentes.

La frecuencia de este cambio puede ser definida por la combinación de los movimientos de la tierra con respecto al sol y de la luna. En general el periodo de los componentes de la onda de marea puede variar desde unas pocas horas hasta 18,6 años, sin embargo los de tipo semidiurnos (12 horas) y diurnos (24 horas) son los más predominantes. La ondulación de la superficie del mar asociada con estas frecuencias varía desde unos diez centímetros en mar abierto hasta metros en las costas [5]. Para determinar y separar todos los constituyentes de marea se necesitan series de tiempo razonablemente largas (18,6 años). Determinaciones de largos periodos de tiempo de la amplitud de las mareas son realizadas con el uso de medidores del nivel de agua ó de presión. Recientemente la altimetría satelital también ha sido usada para medir la elevación de la marea [6]. La predicción de la marea es convencionalmente llevada a cabo usando el análisis de armónicos. En este los datos de las series de tiempo de la elevación de la superficie del mar son analizados para determinar la amplitud y la fase de los constituyentes más importantes los cuales pueden ser combinados para predecir la marea[7].

Lord Kelvin, a quien también se le atribuye la invención del mareógrafo, fue el primero en proponer el análisis de armónicos alrededor del año 1867[5]. A partir de sus planteamientos, Darwin [8, 9, 10] formuló un método más práctico y útil para analizar las mareas. Doodson [11] perfeccionó la teoría de Kelvin para elaborar un tratamiento más formal de los periodos de los astros; su simbolismo es aún usado hoy para denotar varios constituyentes. Munk y Carwright [12] y Carwright [13] formularon el problema de la marea en términos de admitancias para tener en cuenta el espectro continuo del ruido de fondo generado por la marea meteorológica (método de respuesta). Este trabajo, sin embargo, significó cambios muy pequeños en los procedimientos prácticos del análisis de mareas. Así desde las técnicas introducidas por Doodson, el análisis de armónicos permaneció invariable por cerca de 100 años. Las mejoras ocurridas desde 1921, están relacionadas con remover los efectos de los constituyentes menores que no pueden ser determinados con un año de datos, correlaciones de una estación de medición a otra, una especificación más precisa de los periodos astrales, tratamiento de datos irregularmente espaciados y desarrollo de software numéricamente eficiente [4, 14].

El método de análisis de constituyentes de mareas por mínimos cuadrados fue presentado por Foreman [14, 15]. El objetivo de este es estimar la fase y la amplitud de los constituyentes armónicos de la marea, los cuales pueden ser posteriormente usados para predicciones de largos periodos [7]. Este método permite encontrar una solución con cientos de constituyentes, de los cuales 45 son típicamente de origen astronómico, identificados con una frecuencia específica. Los constituyentes restantes incluyen los de aguas pandas y otros asociados con los efectos de la fricción del fondo, términos no lineales en la ecuación de movimiento y finalmente los originados por efectos atmosféricos [7]. Para asegurar que todos los constituyentes sean incluidos en la predicción, se requiere una serie de tiempo de datos de marea de largo periodo, idealmente mayor a 18.6 años. Desafortunadamente, estos datos no siempre están disponibles con esta extensión, lo cual puede conllevar a la consecución de soluciones inestables o con residuales altos, si se quiere separar la totalidad de los armónicos de marea, unos 500 en total[16, 17].

El análisis de armónicos permite determinar los coeficientes y para la frecuencia especifica M. En este caso, q =0,1,…, M y , de manera tal que hay un total de 2M+1 constituyentes armónicos. Se asume que hay más observaciones N, que coeficientes específicos (2M+1<<N). El problema de ajustar M curvas armónicas para la serie de tiempos debe ser resuelto usando técnicas de optimización. La amplitud y la fase de varios componentes pueden ser encontradas minimizando las diferencias cuadradas entre la serie de tiempos original y la serie ajustada [7]. El coeficiente de cada constituyente es encontrado mediante la solución de una matriz (M+1) X (M+1). Para M posibles constituyentes armónicos, las series de tiempo pueden ser expandidas como lo expresa (1).

(1)

En la cual es el valor medio de las mediciones, es la porción residual de la serie de tiempo (la cual puede contener otra clase de constituyentes armónicos), , n = número de pasos del tiempo y , son respectivamente, las constantes de amplitud, frecuencia y fase del enésimo constituyente señalado. En esta configuración se asume que la frecuencia especificada tiene la forma . Reformulando (1) en los términos de los coeficientes desconocidos y tenemos:

(2)

Donde:

;

para q=0,…,M. El objetivo del análisis de mínimos cuadrados es minimizar la variancia, , del residual de la serie de tiempo en la siguiente ecuación.

(3)

En la ecuación 3 se ha definido como:

(4)

Tomando derivadas parciales de (3) con respecto a los coeficientes desconocidos y , e igualando los resultados a cero, tenemos 2M+1 ecuaciones simultaneas para M+1 constituyentes.

(5)

(6)

La derivación de los coeficientes en la ecuación 6 requiere la solución de una matriz de forma DZ=y, en la cual D es una matriz (M+1)X(M+1) que involucra las sumatorias de seno y el coseno, y es un vector columna que incorpora la serie de tiempos de observaciones y Z es una matriz de los coeficientes requeridos y . Para los detalles de la inversión de la matriz y los problemas relacionados, los lectores son referidos a Foreman [14]. Para simplificar la sumatoria de la ecuación 6, son empleados el seno y el coseno. Esto requiere que los datos estén uniformemente espaciados y que la matriz de términos sea calculada a partir de la serie de tiempos sin faltantes. La matriz D resultante es simétrica, así que solo la parte superior del triángulo consistente de 2M+3M+1 elementos necesita ser almacenada durante la ejecución de los cálculos. La solución de Z se encuentra a través de (7).

Z=D-1*y (7)

Donde D-1 es la inversa de la matriz

(8)

Mientras que los vectores y, z corresponden a la forma.

; (9)

Los elementos de Z requieren los coeficientes y , por cada coeficientes de constituyente armónico especificado. Para encontrar esta solución, se debe sustituir los elementos de D para los pasos del tiempo y usando , . En estas expresiones, y son unidades de frecuencia de y T=N es la longitud de los datos.

En nuestro país muy pocas investigaciones han sido efectuadas para caracterizar los principales componentes de marea en el mar Caribe Colombiano. Una de ellas es el estudio realizado por Molares [18] quien analizó las series de tiempo de nivel del mar de Cartagena, las Islas del Rosario y San Andrés Isla, para identificar los principales constituyentes armónicos, y caracterizó la marea de estos lugares usando el criterio de Courtier. En la bahía de Santa Marta, no hay disponibilidad de datos de mediciones de niveles del mar que permitan hacer inferencias sobre las características de las mareas. En este artículo se presenta el reporte de las mediciones de la marea efectuadas en la bahía de Santa Marta. Con los datos medidos se efectuó un análisis de armónicos para determinar los constituyentes de la marea, así como su clasificación.

2. MATERIALES Y METODOS

2.1 Área de estudio
La bahía de Santa Marta se ubica entre los 11,21 y 11,25 de latitud norte y -74,20 y -74,23 de longitud oeste en el Mar Caribe. La localización de la misma se puede apreciar en la figura 1, donde a la vez se muestra la ubicación de la estación de medición (11,25 Lat., -74,22 Long.)

Figura 1: Localización estación de medición en la bahía de Santa Marta.
Figure 1. Measurement station localization at Santa Marta bay

2.2 Equipos de Medición
Se utilizó un medidor de niveles de agua WLR 7 (Water Level Recorder por su sigla en ingles) marca Aanderaa. El WLR fue instalado en el fondo marino mediante una base de concreto de 50 Kg de peso (ver figura 2) y equipado con un transductor de presión de cuarzo 3187B con rango de 0-700 Kpa, que registra los datos de presión a intervalos regulares de tiempo y elimina las fluctuaciones generadas por las olas. Las lecturas de presión fueron convertidas posteriormente a profundidad de lámina de agua y luego a nivel de elevación de la superficie del mar, restando la profundidad de fondeo. El intervalo de medición de los datos fue de una hora, de julio 1 a agosto 31 de 2008.

Figura 2. Instalación del WLR 7 para las mediciones de marea en la bahía de Santa Marta
Figure 2. WRL7 installation to tide measurements at Santa Marta bay

2.3 Registro de profundidad y localización
Para determinar la profundidad exacta de instalación del equipo WLR7, se utilizó una ecosonda marca Garmin modelo FishFinder 300C de registro en pantalla con una capacidad de lectura de hasta 275 metros. Esto permitió la posterior conversión de los datos de presión a niveles de mar. La posición geográfica se determinó mediante un GPS MAP 100 Garmin.

2.4 Análisis de armónicos
Se usó el paquete T_TIDE [20], que corresponde a una versión en Matlab del software de análisis de armónicos escrito en Fortran [14,15]. Este ajusta los constituyentes de marea por el método de mínimos cuadrados con frecuencias preestablecidas. Cuando la serie de tiempos de niveles de la elevación de la superficie del mar es corta (menor a un mes), los constituyentes que tienen un periodo mayor a 720 horas no son incluidos, por tanto hay una gran incertidumbre asociada a las estimaciones realizadas [20]. La forma como el software resuelve este problema y en general los aspectos de la determinación de parámetros de mareas son discutidos por Rosenfeld [21]. En este caso los constituyentes semidiurnos K2 y S2 y los diurnos K1 y P1 no pueden ser explícitamente resueltos y deben ser incluidos automáticamente por el paquete para lo cual se utiliza el criterio Rayleigh. [7, 22]. Los constituyentes son seleccionados de acuerdo a la longitud del registro de datos [14,15]. Dado un registro de datos de n muestras espaciadas un intervalo de tiempo , el criterio de Rayleigh establece como frecuencia mínima de resolución el valor de [22]. Los constituyentes son seleccionados basados en su importancia relativa esperada frente a la serie de tiempo de mediciones y la posibilidad de separación de la frecuencia. Mayor información y detalles sobre este procedimiento puede ser consultada en Leffler [1], Pawlowicz [20] y Kang [22].

De acuerdo a la convención del análisis de armónicos usada en el paquete T_TIDE, la onda de marea es representada con la amplitud y la fase. La fase está relacionada con el meridiano de Greenwich y su unidad es en grados. Para la selección de las componentes presentes en la serie de tiempo se utilizó el criterio de comparación de Rayleigh [18, 23]. Esta comparación decide cuando un constituyente específico debe ser incluido en el análisis. Si es la frecuencia de una componente a incluir en el análisis, es la frecuencia de una componente ya incluida (componente de comparación) y el periodo de tiempo de datos a analizar, la componente en cuestión se incluirá sólo si . Este método determina por separado las dos componentes implicadas. Si la componente de frecuencia ya está incluida, para que la componente de frecuencia pueda determinarse, será necesario que sea como mínimo igual al periodo del desfase entre ambas componentes .

El error entre los datos medidos y las predicciones, se determinó mediante el cálculo de los residuales, además de la cuantificación del error de la raíz media cuadrática (RMS) [24] y la habilidad predictiva (Skill) [25]. La expresión del error de la raíz media cuadrática se muestra en la ecuación (10), mientras que la cuantificación de la habilidad predictiva se realizó de acuerdo a la ecuación (11).

(10)

(11)

Donde y son los niveles de agua (m) medidos y ajustados respectivamente, N es el número de datos horarios con que cuentan las series de tiempo y . corresponde a la media temporal de los niveles de agua de la predicción.

3. RESULTADOS

3.1 Profundidad de instalación.
La profundidad a la cual se instalaron los equipos es un control necesario en el procesamiento de los datos de presión y su conversión a niveles de agua. El medidor WLR7 se fondeo a 22 metros.

3.2 Mareas
Las mediciones de marea mostraron un rango de 48 cm. La variación de estas se presenta en la figura 3 para el periodo comprendido entre julio 1 y agosto 31 de 2008.

Figura 3. Variación del nivel de marea en la bahía de Santa Marta (01/07/08 -31/08/08).
Figure 3. Sea level variation at Santa Marta bay (01/07/08 -31/08/08).

Durante el día ocurren dos elevaciones máximas, una más pronunciada que otra; los niveles mínimos tienen el mismo comportamiento. Según esta observación la marea en la bahía de Santa Marta es de tipo mixta.

3.3 Identificación de componentes de marea
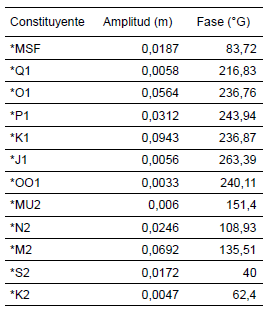
En el análisis armónico se identificaron y separaron 37 constituyentes, 12 de estos resultaron ser significativos con un nivel del significancia del 95% (figura 4). La amplitud y fase de los mismos se presentan en la tabla 1. Para detalles de la forma como se calcula el nivel de significancia los lectores son referidos a Leffler [1] y Pawlowicz [20]. Se encontraron seis constituyentes de carácter diurno (K1, O1, P1, Q1, J1, OO1) y cinco de carácter semidiurno (M2, S2, K2, N2, Mu2), el restante corresponde a la componente lunisolar sinódica quincenal (Msf). Los componentes diurnos resultaron ser más representativos con el 58,3 % de la suma de las amplitudes, frente al 36,1 % de los componentes semidiurnos.

Figura 4. Identificación de componentes significativos en la serie de tiempos de marea en la bahia de Santa Marta.
Figure 4. Significative tide constituents identification from tide measurements at Santa Marta bay

Tabla 1. Constituyentes de marea significativos.
Table 1. Significative tide constituents

3.4 Predicción de la marea
Se compararon las mediciones con las predicciones realizadas utilizando los constituyentes separados desde la serie de datos de mareas medidos. El RMS entre los datos medidos y las predicciones, fue menor a 2 cm (1,1 cm). El resultado de la habilidad predictiva fue de 0,99. Una concordancia buena entre los datos medidos y las predicciones genera un Skill de uno y por el contrario un desajuste completo entre estas series de tiempo arroja un skill de cero. Los valores superiores a 0,95 para este parámetro son considerados representativos de un buen acercamiento de las predicciones a los datos medidos [26], lo cual es el caso reportado en este estudio. En la figura 5 se presenta la comparación entre las mediciones y las predicciones de la marea para la bahía de Santa Marta, además de los residuales. Los valores máximos y promedios de los residuales fueron de 3,8 cm y 0,8 cm respectivamente. La utilización de los armónicos identificados permite representar el 96% de la marea reportada por el medidor WLR.

Figura 5. Comparación de serie de tiempo de mediciones y predicciones en la bahía de Santa Marta.
Figure 5. Measurements and predictions time series comparation at Santa Marta bay.

3.5 Clasificación de la marea
Las mareas en una región en particular pueden ser caracterizadas por la relación en las magnitudes relativas de las amplitudes de los constituyentes principales diurnos y semidiurnos [27] definida como el coeficiente de Cartier, cuya expresión matemática es presentada por (12).

(12)

Donde; corresponde al coeficiente de Cartier, = amplitud (m) de la componente diurna lunisolar, = amplitud (m) componente lunar diurna, = amplitud (m) Componente lunar principal semidiurna y = amplitud (m) componente solar principal semidiurna. Burlin [27] sugiere que un Nf<0,25 resulta en mareas semidiurnas, mientras que un Nf>3,0 corresponde a mareas diurnas. Para 0,25 < Nf < 1,5 las mareas son mixtas principalmente semidiurnas, mientras que para 1,5 < Nf < 3,0 las mareas son también mixtas pero principalmente diurnas. Para el caso de la bahía de Santa Marta las mareas son mixtas principalmente diurnas (Nf=1,74).

4. DISCUSIÓN

El objetivo en el tratamiento de datos de mediciones de marea, es la separación matemática por análisis de armónicos de ciertos componentes periódicos los cuales pueden ser usados para simular la marea astronómica. Tradicionalmente esta es representada por la suma finita de constituyentes armónicos, cada uno de ellos debido a un aspecto particular de las fuerzas productoras de mareas. Una vez determinados, el mismo set de parámetros que gobiernan cada componente periódico pueden ser usados para predecir la marea durante un periodo de tiempo deseado en un determinado lugar. Aunque diferentes métodos han sido desarrollados para determinar estos constituyentes de marea, rara vez se encuentran métodos que puedan ser usados por personal no especializado. Entre los de rápida comprensión, está el método de los mínimos cuadrados, el cual es fácil de programar e implementar y con la ventaja adicional de tener muy pocos requerimientos de memoria. Este es más eficiente cuando es usado para obtener un número fijo de constituyentes armónicos de marea a partir de mediciones discretas de elevaciones del nivel del mar. Una serie de tiempo de longitud mínima apropiada para implementar este método consiste en mediciones horarias que cubran un periodo sinódico mensual (aproximadamente 29 días). Una serie de esta longitud temporal permite separar 10 de los constituyentes principales que forman la marea astronómica.

Para esta investigación el cálculo de las amplitudes y las fases de Greenwich de las componentes de la marea se realizó mediante el método de análisis armónico de ajuste por mínimos cuadrados [4]. Se empleó el paquete de programas en Matlab T_TIDE [20]. Este puede desarrollar el clásico análisis de armónicos para periodos de hasta un año ó con una extensión menor de tiempo y calcula el intervalo de confianza para los componentes analizados. Idealmente los análisis armónicos se realizan con series de tiempos de datos con periodos de un año o superiores, esta condición permite identificar y separar la mayoría de los constituyentes armónicos. Con una serie de tiempos de 18.6 años, periodo correspondiente a la inclinación lunar orbital, se pueden identificar hasta 500 constituyentes. Sin embargo este registro ideal para datos de marea no se encuentra con facilidad, lo que permitió que las técnicas de análisis evolucionaran hasta poder separar constituyentes desde registros cortos de un mes de datos horarios. El procedimiento de Foreman para el método de mínimos cuadrados identifica 45 constituyentes astronómicas y 24 de aguas poco profundas de registros de mareas de un año de extensión. En la práctica los registros de mareas escasamente exceden el año de mediciones, por tanto, el procedimiento aquí mostrado es útil para estas situaciones.

El conjunto de datos analizados, consta de una serie de tiempo horaria con 60 días de extensión, la respuesta de los armónicos identificados incluye constituyentes de corto periodo (diurnos y semi diurnos). Otros componentes de periodos de medio año, mensuales y semimensuales pudieron estar excluidos del ajuste de la marea de Santa Marta, dada la longitud de la serie de tiempos de observaciones usadas. Además de los componentes diurnos y semidiurnos que se ajustaron a las mediciones, se encontró la componente lunisolar sinódica quincenal (Msf), cuyo periodo es de 354,4 horas. Esta fue la única con periodo diferente a 12 o 24 horas incluida en el grupo de armónicos separados. Es de esperarse que con una serie de tiempo de mayor extensión, se puedan identificar otras componentes de períodos mayores a los quincenales. Sin embargo, sólo la extensión de la serie de tiempo, no es determinante para que un grupo de constituyentes se ajusten a las observaciones, ello puede evidenciarse del hecho que otros componentes de tipo sexto diurno o quincenales, cuyo periodo es inferior a la extensión de la serie de tiempo analizada, no resultaron representativos para la marea en Santa Marta. Los constituyentes en este método son estimados estadísticamente por su significancia, lo que permite que su selección sea confiable.

5. CONCLUSIÓN

La marea en el área de la bahía de Santa Marta tiene un rango mareal de 48 cm y una clasificación mixta principalmente diurna, lo que coincide con lo reportado [18] para otras regiones cercanas del Caribe Colombiano, como Cartagena y las Islas del Rosario.

Los constituyentes principales de armónicos separados en las series de tiempos de datos horarios medidas durante 60 días en la bahía de Santa Marta, corresponden a seis de carácter diurno (K1, O1, P1, Q1, J1, OO1), cinco de carácter semidiurno (M2, S2, K2, N2, Mu2) y la componente lunisolar sinódica quincenal (Msf).

AGRADECIMIENTOS

Los autores agradecen a COLCIENCIAS y las universidades del Magdalena y de Antioquia por la financiación brindada para la ejecución de este estudio.

REFERENCIAS

[1] LEFFLER, K. E. AND JAY, D. A. Enhancing tidal harmonic analysis: Robust(hybrid L1=L2) solutions, Continental Shelf Research., 29, 78- 88. 2009.
[2] FLINCHEMA, E.P AND JAY, D.A. An Introduction to Wavelet Transform Tidal Analysis Methods, Estuarine, Coastal and Shelf Science, 51, 177-200, 2000.
[3] SHENOI, S.C., GOUVEIA, A. AND SHETYE, S.R. Diurnal and semi-diurnal tidal currents in the deep mid-Arabian Sea, Proc. Indian Acad. Sci. (Earth Planet. Sci.), 101(2), 177-189, 1992.
[4] GODIN, G. The analysis of tides, Univ. of Toronto Press, Toronto, 1972.
[5] EMERY, J.E. AND THOMSON, R. Data analysis methods in physical oceanography. Elsevier ed., Amsterdam, 2004.
[6] FORRESTER, W.D. Canadian Tidal Manual. Department of Fisheries and Oceans, Ottawa, 1983.
[7] CARTWRIGHT, D.E., AND RAY, R.D., Oceanic tides from geosat. Altimetry, Journal of Geophysical Research, 95, 3069-3090, 1990.
[8] DARWIN, G. H. A general article on the tides. In Admiralty Scientific Manual. The Admiralty, London, 91 P. 1886. en: FLINCHEM, E., AND JAY, D.A. An Introduction to Wavelet Transform Tidal Analysis Methods, Estuarine, Coastal and Shelf Science, 51, 177-200, 2000.
[9] DARWIN, G. H. On tidal prediction. Philosophical Transactions of the Royal Society of London A182, 159-229. 1981. en: FLINCHEM, E., AND JAY, D.A. An Introduction to Wavelet Transform Tidal Analysis Methods, Estuarine, Coastal and Shelf Science, 51, 177-200, 2000.
[10] DARWIN, G. H. On an apparatus for facilitating the reduction of tidal observations, Proceedings of the Royal Society of London A52, 345-389. 1893. en: FLINCHEM, E., AND JAY, D.A. An Introduction to Wavelet Transform Tidal Analysis Methods, Estuarine, Coastal and Shelf Science, 51, 177-200, 2000.
[11] DOODSON, A. T. The harmonic development of the tidegenerating potential. Proceedings of the Royal Society of London A100, 305-329. 1922. en: FLINCHEM, E., AND JAY, D.A. An Introduction to Wavelet Transform Tidal Analysis Methods, Estuarine, Coastal and Shelf Science, 51, 177-200, 2000.
[12] MUNK, W. H. AND CARTWRIGHT, D. E. Tidal spectroscopy and prediction. Philosophical Transactions of the Royal Society of London A259, 533-581. 1965. en: FLINCHEM, E., AND JAY, D.A. An Introduction to Wavelet Transform Tidal Analysis Methods, Estuarine, Coastal and Shelf Science, 51, 177-200, 2000.
[13] CARTWRIGHT, D. A unified analysis of tides and surges round north and east Britain. Philosophical Transactions of the Royal Society of London A263, 1-55. 1968. en: FLINCHEM, E., AND JAY, D.A. An Introduction to Wavelet Transform Tidal Analysis Methods, Estuarine, Coastal and Shelf Science, 51, 177-200, 2000.
[14] FOREMAN, M.G.G. Manual for Tidal Heights Analysis and Prediction. Pacific Marine Science Report 77-10, Institute of Ocean Sciences, Patricia Bay, Sidney, 1977.
[15] FOREMAN, M.G.G. Manual for Tidal Currents Analysis and Prediction. Pacific Marine Science Report 78-6, Institute of Ocean Sciences, Patricia Bay, Sidney, 1978.
[16] FORRESTER, W.D. Canadian Tidal Manual. Department of Fisheries and Oceans, Ottawa, 1983.
[17] TIANHANG, H. Sequential Tidal Analysis and Prediction. M.Sc. thesis. Department of Geodesy and Geomatics Engineering, University of New Brunswick, Fredericton, N.B., Canada, 1991.
[18] MOLARES, R. Clasificación e identificación de las componentes de marea del Caribe Colombiano, Boletín científico, 22, 105-114, 2004
[19] BARTELS, G. Geomorphologische Höhenstufen der Sierra Nevada de Santa Marta (Kolumbien), Giessener Geogr. Schr., 21, 1-56, 1970.
[20] PAWLOWICZ, R., BEARDSLEY, B. AND LENTZ, S., Classical tidal harmonic analysis with errors in matlab using t-tide, Computers & Geosciences, 28, 929-937, 2002.
[21] ROSENFELD, L., SHULMAN, I., COOK, M., PADUAN, J., AND SHULMAN, L. Methodology for a regional tidal model evaluation, with application to central California Deep Sea Research Part II, Topical Studies in Oceanography, 56(3-5), 199-218, 2009.
[22] KANG, W. J., MOON, S. J., PARK, S. J. AND LEE, K. Analyzing sea level rise and tide characteristics change driven by coastal construction at Mokpo Coastal Zone in Korea, Ocean Engineering, 36, 415-425, 2009.
[23] FOREMAN, M.G. AND NEUFELD, E.T. Harmonic tidal analyses of long time series, International Hydrographic Review, 68(1), 85-108, 1991.
[24] DIAS, J.M. and LOPES, J.F. Implementation and assessment of hydrodynamic, salt and heat transport models: the case of Ria de Aveiro lagoon, Portugal, Environmental Modelling and Software, 21, 1-15, 2006.
[25] LI, M., ZHONG, L. AND BOICOURT, W.C. Simulations of Chesapeake Bay estuary: sensitivity to turbulence mixing parameterizations and comparison with observations, Journal of Geophysical Research, 110 (C12004), 2005.
[26] DIAS, J.M. SOUSA, M.C., BERTIN, X. FORTUNATO, A. AND OLIVEIRA, V. Numerical modeling of the impact of the Ancão Inlet relocation (Ria Formosa, Portugal), Environmental Modelling and Software, 24, 711-725, 2009.
[27] BURLING, M., PATTIARATCHI, B. AND IVEY, G. The tidal regime of Shark Bay, Western Australia, Estuarine, Coastal and Shelf Science, 57, 725-735, 2003.