Fingerprint verification using computational geometry

This paper presents a robust minutiae based method for fingerprint verification. The proposed method uses Delaunay Triangulation to represent minutiae as nodes of a connected graph composed of triangles. The minimum angle over all triangulations is maximized, which gives local stability to the constructed structures against rotation and translation variations. Geometric thresholds and minutiae data were used to characterize the triangulations created from input and template fingerprint images. The effectiveness of the proposed method is confirmed through calculations of false acceptance rate (FAR), false rejected rate (FRR) and equal error rate (EER) over FVC2002 databases compared to the results of other approaches.

DOI: https://doi.org/10.15446/dyna.v83n195.46323

Verificación de huella dactilar utilizando geometría computacional

Manuel Ramírez-Flores ^a, Gualberto Aguilar-Torres ^b & Gina Gallegos-García ^c

^a Sección de Estudios de Posgrado e Investigación, Instituto Politécnico Nacional, Unidad Culhuacán, México. manuel300688@gmail.com
^b Comisión Nacional de Seguridad, México D.F., México, autg79y@yahoo.com
^c Sección de Estudios de Posgrado e Investigación, Instituto Politécnico Nacional, Unidad Culhuacán, México. ggallegosg@ipn.mx

Received: October 17^th, 2014. Received in revised form: August 12^th, 2015. Accepted: January 10^th, 2016.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
This paper presents a robust minutiae based method for fingerprint verification. The proposed method uses Delaunay Triangulation to represent minutiae as nodes of a connected graph composed of triangles. The minimum angle over all triangulations is maximized, which gives local stability to the constructed structures against rotation and translation variations. Geometric thresholds and minutiae data were used to characterize the triangulations created from input and template fingerprint images. The effectiveness of the proposed method is confirmed through calculations of false acceptance rate (FAR), false rejected rate (FRR) and equal error rate (EER) over FVC2002 databases compared to the results of other approaches.

Keywords: Angle of orientation, Delaunay Triangulation, Equal Error Rate, Fingerprint, Geometric Thresholds.

Resumen
Este trabajo presenta un método robusto con base en minucias para la verificación de huellas dactilares. El método propuesto utiliza Triangulaciones de Delaunay para representar a las minucias como nodos de un grafo compuesto por triángulos. El ángulo mínimo sobre todas las triangulaciones es maximizado, lo cual proporciona estabilidad local a las estructuras construidas contra variaciones de rotación y traslación. Umbrales geométricos y datos sobre minucias fueron utilizados para caracterizar las triangulaciones creadas con las imágenes de huellas dactilares de entrada y plantilla. La efectividad del método propuesto es confirmada con cálculos de la tasa de falsa aceptación (FAR), tasa de falso rechazo (FRR) y la tasa de igualdad de error (EER) sobre las bases de datos FVC2002, en comparación con los resultados de otras propuestas.

Palabras clave: Ángulo de orientación, Triangulaciones de Delaunay, Tasa de Igualdad de Error, Huella Dactilar, Umbrales Geométricos.

---

1. Introduction

Biometric technologies use some physical or psychological trait such as: fingerprint, face, iris, voice, etc. to verify or identify individuals and therefore restrict unauthorized access to computational systems. These traits are unique and inherent in individuals, making it difficult to falsify their I.D.; however, often they are noisy by nature [1].

Three types of degradations normally affect the quality of the fingerprint image: appearance of gaps between ridges, parallel ridges intercepts and natural effects such as cuts, wrinkles and injuries. Image enhancement processes are in charge of improving the contrast between ridges and valleys, and reducing the noise in the image [2]. Sometimes methods similar to medical image processing are also used, for example, via spatial domain filtering [3].

After enhancing the fingerprint image, comes the process of extracting and matching fingerprint features, which can be classified in three categories: based on minutiae [4-6], based on image [7-9] and hybrid [2,10,11]. Those based on minutiae, use a feature vector extracted from fingerprints as a set of points in a multi-dimensional plane. Some of the characteristics that the feature vector represents are: type of minutiae, position, and orientation, among others. After the extraction process, fingerprint matching becomes a non-rigid point-matching problem with unknown correspondence and differences in the number of points belonging to two sets (query and template). Moreover, skin elasticity changes the relative position of the minutiae at each acquisition [6] and can cause genuine minutiae to get lost or pseudo minutiae to appear. [5]

The use of computational geometry can help to address image-processing problems that are difficult to understand and implement, such as distortion, rotation variations, and some others. One particular geometric structure that can resolve most of the shortcomings in the minutiae based methods for fingerprint verification processes is a Delaunay Triangulation.

For fingerprint verification processes, Delaunay Triangulation can be formed if the minutiae locations are taken as the set of points P. The advantages of this proposed method are that every minutia keeps the same neighboring structure even in the presence of distortion. Insertion of new points in the triangulations because of noise affects only locally. The same happens with missing or spurious minutiae. Thus, using geometrical thresholds, each triangle in the Delaunay Triangulation can be characterized uniquely. Because of this, each fingerprint can be classified and when a second sample of the same fingerprint requires to be verified, a quantitative comparison can be made. An Equal Error Rate of less than 1% can be obtained using these techniques, demonstrating the accuracy of the method under these thresholds.

1.2. Our contribution

The novelty of our contribution with respect to other approaches is in the full analysis of the Delaunay Triangulations to compare minutiae structures between fingerprints. Most minutia based approaches that use Delaunay Triangulations start their analysis by studying the edges that form Delaunay triangles instead of analyzing these triangles as a basic structure [4-6]. In some cases, even a threshold is established to decide whether to use Delaunay Triangulations or whether to process all possible combinations of minutiae forming an edge [4]. This kind of analysis involves a greater computational load because of the number of combinations to analyze and the operations required for each comparison.

On the other hand, if Delaunay Triangulations are used, most of the approaches presented until now perform a fingerprint alignment based on one reference triangle. To find this reference triangle an analysis of the triangle's edges is undertaken by using specific thresholds. Then, after the alignment, other thresholds have to be established to define a neighborhood where aligned minutiae should be. With this, several alignments and comparisons have to be made in order to count the matching aligned minutiae, calculate a matching score and find the best alignment [5,6].

In our proposal, from the beginning, every Delaunay triangle extracted from the query fingerprint is compared against every triangle extracted from the template fingerprint. In this comparison, the analysis of the three edges of the triangle and the three vertices of the triangle are performed. To avoid fingerprint alignment operations, a measurement and a comparison of the orientation of the triangles is performed. By establishing a specific threshold, the possible variation of fingerprint rotation is considered.

In the case of spatial displacement of the fingerprints, the structure of the Delaunay Triangulation is tolerant because if a general spatial displacement takes place, then all the minutiae move by the same proportion and the triangles extracted remain the same. If only some minutiae were displaced, then the length of the sides of some triangles changes, and the threshold for the comparison of the length of triangles covers that distortion. Finally, the matching score for the comparison of two fingerprints is pretty straightforward. The matching score is calculated as the rate of coincident triangles over the average of the total number of triangles between both fingerprints.

This paper is organized as following: Section 2 describes related work around the problem of fingerprint verification. Section 3 explains the mathematical and computational theory behind Delaunay Triangulations and the measurements calculated from this to characterize a fingerprint. Section 4 details our proposed solution and how our scheme was implemented, pointing out the tools used for the extraction of the fingerprint feature vector and the thresholds used in the matching process. Section 5 shows the results obtained after applying the proposed solution to 4 FVC2002 databases. Then a discussion of these results is presented. Finally, Section 6 contains the conclusions of this work in terms of the results obtained and the future work to improve the performance of the scheme proposed.

2. Related work

2.1. Image based approaches

Many studies have been undertaken to deal with the problem of fingerprint matching and many algorithms and schemes with different approaches have been proposed. Among image-based methods for fingerprint verification, there is a proposal based on features extracted from Wavelet and Fourier-Melling Transform (WFMT). Wavelet transform is used to preserve the local edges and reduce noise in the low frequency domain after image decomposition, which makes the fingerprint image less sensitive to shape distortion. Then Fourier-Melling transformation (FMT) served to produce a translation, rotation and scale invariant feature. The results obtained in [7], show that verification accuracy is 5.66 and EER is of 1.01%.

A second proposal in the category of image-based algorithms is the use of tessellated invariant moment features for fingerprint verification. In this scheme, a reference point is proposed to allow more accurate and quicker performance. In the scheme, all the intrinsic properties of the fingerprints are estimated, such as foreground region mask, local ridge orientation and local ridge frequency, to enhance fingerprint image. By using different complex filtering methods, a reference point is established. Then its orientation is calculated using the least mean square orientation algorithm. A Region of Interest (ROI) is centered on the reference point and tessellated in a predefined number of square cells. Seven invariant moments are extracted from the cells and these represent the fingerprint information of the local structure. The verification is based on measurements similar to the eigenvalue-weighted cosine (EWC) distance to match two corresponding feature vectors. The experiments carried out over the FVC2002 4 databases show an average Equal Error Rate (EER) of 3.57% using the EWC distance [8].

2.2. Hybrid approaches

One solution for hybrid fingerprint extraction and matching processes was proposed in [10] and uses both minutiae and ridge flow information. To capture the ridge strength at equal space orientations, a set of 8 Gabor filters in the spatial frequencies that correspond to the average inter-ridge spacing in fingerprints is used. Then an eight-dimensional ridge feature map is constructed with square tessellation of the filtered images. This map and the minutiae set of a fingerprint are used for matching purposes. For this scheme, the calculated EER is about 4%.

2.3. Minutiae based approaches

Thus, regarding the proposals in the minutiae based category for fingerprint matching, there are few researches that utilize Delaunay Triangulations as a structure to compare a query and a template fingerprint image. In 2004, Parziale and Niel, proposed to establish the dependency among minutiae by applying Delaunay Triangulation over the point set representing them. In that structure, each minutia was used as a triangle's vertex. Then measures of distance between minutiae pairs, angular difference between orientations of minutiae pairs, and angles between the orientation of each minutia and the segment connecting them with another minutia, were calculated.

After applying three geometric filters, some triangulations in the query set were selected as candidates for matching with the triangles of the template set. For that, an alignment procedure was undertaken with the triangulations in the query set in terms of spatial coordinates and angles of orientation. If a minutia in the transformed query set is close enough to a minutia in the template set, it is counted and used later to calculate a matching score. [6]

In 2005, Liu, Yin, and Zhang, proposed a very similar fingerprint matching algorithm based on Delaunay Triangulations to find reference minutiae pairs known as RMPs. The analysis using Delaunay Triangulations begins with similar edge pairs formed from query and template sets of minutiae. Measurements of Euclidian distance, minutia orientation and edge orientation are then compared. If a pair of edges is very similar, then the triangles to which they belong become candidates for the next analysis phase. In the second phase, the distance of triangle's sides and internal angles are compared. If a coincidence between triangles exists, for each triangle, an alignment of the query set with the template set is carried out, using geometrical equations. Finally, for each alignment of points, these are counted and a matching score is calculated. [5]

The last proposal related to the use of Delaunay Triangulations, was made by Deng and Huo in 2005. Instead of finding the best-matching minutiae pairs, the objective was to find the best-matching edge pairs. Other important changes were: minutiae orientation was mapped to a range from 0 to 2P instead of using the original from 0 to P. The ridge count between minutiae was also used as data in the matching process.

The process of fingerprint matching starts by checking the number of minutiae in the fingerprint image, if it is below a threshold, Delaunay Triangulations are not calculated and instead all the possible edges connecting two minutiae are considered. Then, several geometric filters are applied to the edge pairs, like Euclidean distance, minutiae orientation difference, among others. Only the minutiae of the edges that satisfy those filters are used in the next phase. The remaining minutiae are sorted in ascending order and form all the possible triangles with the closest neighboring minutiae. Again, geometric comparisons between triangles are performed. If their characteristics satisfy the thresholds established, a matching score is calculated for each triangle. At the end, another matching score between the query and template image is calculated considering the triangle matching scores previously calculated. [4]

In later sections of this paper, some of these different schemes will be looked at again in a comparison against our proposed minutiae-based solution. Following that, we present a discussion about the obtained results in terms of the EER, FAR and FRR thresholds.

3. Background

A Triangulation can be defined, as the maximal planar subdivision whose vertex set is P, where P denotes a finite set of points in a plane. A maximal planar subdivision is a subdivision in which no edge connecting two vertices can be added to it without destroying its planarity (any edge that is not in the subdivision intersects one of the existing edges).

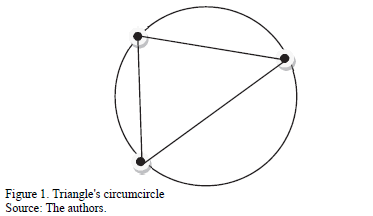
"Let P be a set of points in the plane, and let T be a triangulation of P. Then T is a Delaunay triangulation of P if and only if the circumcircle of any triangle of T does not contain a point of P in its interior."[12]

So any Delaunay Triangulation T maximizes the minimum angle over all triangles that compose it. What is stated in the above quote can be appreciated in Fig. 1.

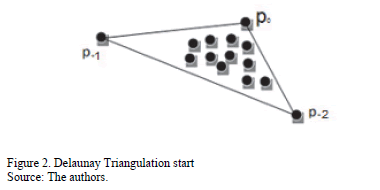
To start building a Delaunay Triangulation with only the set of points P as initial data, an initial repository has to be created. From a geometrical point of view, the repository is the first triangle in the Delaunay Triangulation and it is large enough to contain the whole set of points P. The vertices of the first triangle are: three extra points, p0, p-1 and p-2. Fig. 2 represents this statement.

It is important to choose p₀, p_-1 and p_-2 far enough away, so they do not destroy any triangles in the Delaunay triangulation of P. Later p₀, p_-1 and p_-2 can be discarded together with all their incident edges.

There are basically two types of existing algorithms, which can be used to implement a Delaunay Triangulation: The first type is a static algorithm where the triangulation is valid after every single point is processed. Some examples are: The recursive split algorithm, the divide and conquer algorithm, the step-by-step algorithm, the modified hierarchical algorithm, among others.

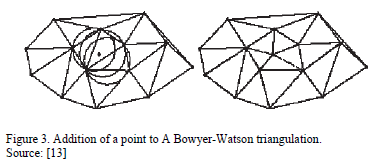
The second type of algorithms is the dynamic triangulation where the triangulation is valid during processing. This makes it possible to view the contribution of one point to the triangulated irregular network (TIN). Some algorithms to implement this are called incremental as the Bowyer and Watson algorithm.

Bowyer and Watson algorithm is known as an incremental delete and build algorithm because it adds points sequentially into an existing Delaunay triangulation [13]. The process follows the steps below:

For each point in set P:

1. Insert point p ∈ P into triangulation
2. Find all existing triangles whose circumscribing circle contains the point p.
3. All triangles found in step 2 are deleted and a convex cavity is created.
4. The point p is joined with all the vertices on the boundary of the cavity formed in 3 (re- triangulation).

Remove initial triangle.

An example of the beginning and the end steps of the process is shown in Fig. 3.

Finally the implementation of the Bowyer-Watson algorithm requires computational data structures such as: point based data structure for the vertices of the triangle, a triangle based data structure for the elements that compose the Delaunay Triangulation and finally a directed acyclic graph that represents the Triangulation with the edges of each triangle and the neighbors that share them.

For the implementation of Delaunay Triangulations in our scheme, the Bowyer and Watson algorithm was used because it provides the same theoretical optimum algorithmic complexity as other methods, which is Q(N log₂ N), but with an easier procedure.

Although Delaunay Triangulations allow the creation of a rotation and distortion tolerant structure, the characterization, identification and comparison between two different triangulations must be undertaken manually. Therefore, the second part of our proposal consists in a set of measures and geometric thresholds that allow to distinguish each triangle and its vertices in the Delaunay triangulations formed.

4. Proposed method

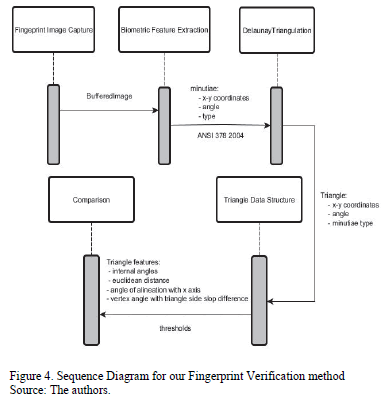
The proposed scheme is a minutia based fingerprint verification system that uses Delaunay Triangulations with geometrical measures and thresholds to validate the similarity between two different fingerprints. The complete proposed scheme is shown in Fig. 4., and explained right after.

Stage 1: Fingerprint image capture.

a. Use of Griaule Biometrics Fingerprint SDK 2009

Stage 2: Minutiae features extraction.

a. Creation of feature extraction vector in ANSI 278-2004 format.

Stage 3: Delaunay Triangulation creation.

a. Creation of reference triangle.
b. Insertion of a new point.
c. Search of the triangle containing the new point inserted.

c.3 Check whether point is already inserted.
c.4 Cross product calculation between vertices of triangle and point inserted.

d. Determine the Cavity produced by the new point in the Delaunay Triangulation.

d.1 Verify whether the new point is inside, on, or outside the Triangle's circumcircle and its neighbors' circumcircles.
d.2 If the new point is inside a circumcircle of some triangle, add it to cavity list.

e. Update Delaunay Triangulation

e.1 Remove triangles contained in the cavity calculated from Delaunay Triangulation.
e.2 Create of new triangles with remaining vertices around the old cavity and the new point.
e.3 Add new Triangles to Delaunay Triangulation.
e.4 Update each link between adjacent triangles.

Stage 4: Triangle Data Structure creation.

a. Triangle's internal angles calculation.
b. Euclidean distance between triangle's vertices calculation.
c. Triangle's angle of alienation with x-axis.
d. Difference between each pair of vertex's angle and triangle side slope.

Stage 5: Triangle features comparison

a. Alignment of triangles based on internal angles.
b. Arithmetic comparison of triangle's vertices based on minutiae type *
c. Arithmetic comparison between the length of the sides of the triangles *
d. Arithmetic comparison of differences between each pair of vertex angle and slope of a triangle side*
e. Arithmetic comparison between angles of alignment with x axis. *
f. Authentication or rejection of fingerprint.

*In each comparison, the corresponding threshold for error tolerance is added.

In Stage 2, the feature vector extracted using the Griaule Biometrics software for each minutia, contains the following biometric data:

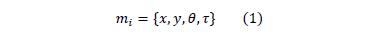
where:

• m_i = ith minutia
• x = value of the spatial coordinate in the x-axis
• y = value of the spatial coordinate in the y-axis.
• q = minutia orientation [0,180°]
• t = type of minutia [end of ridge, ridge bifurcation, other]

For stage 4, different measures are calculated in order to uniquely characterize each triangle. An image interpretation of those calculations can be observed in Fig. 5.

The first measure, related to alignment of triangles can be resumed in Equation (2), which comes from the cosine law for triangles.

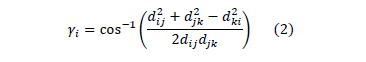
where:

• g_i = triangle's internal angle
• d_ij, d_jk, d_ki = length of triangle's side

An alignment of triangles is needed to ensure that the order in which the vertices of two triangles in different Delaunay triangulations are described is correct. Otherwise, any further calculation will be meaningless because the vertices of the triangles could be swapped. To achieve this, the internal angles of a pair of triangles are paired so that the difference between them is a small as possible.

When a pair of angles has the smallest difference, the vertex of the triangle containing one of the angles is renamed so that it matches with the vertex's name in the other triangle. The process is repeated until the three vertices are matched with the best option in the second triangle. An example is shown in Fig. 6.

Once a pair of triangles is aligned, a process of comparison between the pair of triangles takes place. The first test checks the type of minutiae in the vertices with the same name in the different triangles. The main types of minutiae are classified as: termination and bifurcation.

If the first test is passed, the difference of one triangle's vertex angle (minutia orientation) and the angle of the segment connecting that vertex with another one is calculated, for each of the vertices of a triangle. Equation (3) describes how to calculate this measure. A threshold expressed in grades is established to allow a tolerance limit in the rotation that a triangle can have over another.

where:

• a_ij = angle difference between triangle's side slope expressed as an angle and minutia orientation.
• y_i, y_j = y-spatial coordinate of minutiae i and j respectively.
• x_i, x_j = x-spatial coordinate of minutiae i and j respectively.
• q_i = i's minutia orientation

The next comparison is undertaken using the Euclidean distance equation (4), between the vertices of a triangle. Again a threshold is established, this time in pixels, to tolerate a certain degree of distortion in the shape of the triangle because of the different spatial allocation of the vertices.

where:

• d_ij= Euclidean distance between minutiae i and j
• x_i, x_j = x-spatial coordinate of minutia i and j
• y_i,y_j = y-spatial coordinate of minutia i and j

The final filter is related to Equation (5), which evaluates the angle between the first vertex of a triangle and the x-axis. A threshold expressed in pixels allows a tolerance degree of rotation for the triangle being evaluated in case the fingerprints captured are rotated. It is important to point out that this measure quantifies the degree of rotation that a local area of the fingerprint has in terms of triangles that belong to a Delaunay Triangulation.

With this, an alignment of all minutiae in the fingerprint is no longer needed, given that if there is a rotation of the fingerprint, every minutia and every triangle composed of them will present the variation and it will fit in the threshold established.

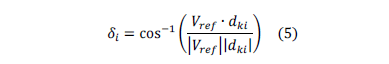
where:

• di = angle between one triangle's side ij and Vref which is a vector parallel to x-axis
• Vref = vector from triangle's minutia mi to y-axis, which is parallel to x-axis
• dki = euclidean distance between minutiae k and i

In the end, if each of the previously mentioned tests are passed successfully then the system recognizes both triangles as the same one and increases the count of equal elements between both of the fingerprint's Delaunay Triangulations.

Equal Error Rates below 1% can be obtained when using these techniques, which is a very good indicator for biometric verification systems.

5. Experiment

Before the experimental section, we must take into account that the fingerprint image obtained always changes due the pressure, angle and the tilt on capture device. For this reason, even if it is the same person, it is almost impossible for the same minutiae to appear in each one of the samples captured. This is one of the factors that mean that fingerprint recognition may present a high percentage of false rejection.

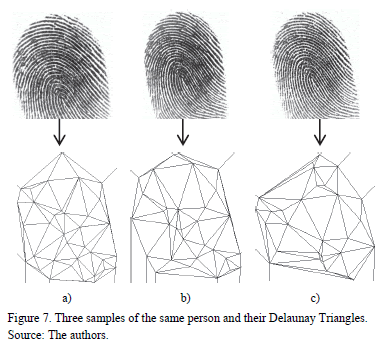
Because of the above, Delaunay Triangulations of the same fingerprint are also different each time a sample is captured, as shown in the Fig. 7.

During the experimental section, different tests were performed and it was found that it is almost impossible to have many similar Delaunay Triangulations in samples of two different fingerprints; however, in two samples of the same fingerprint, we found many similar Delaunay Triangulations. On average, when we have two samples of different fingerprints, we have found a maximum of two Delaunay Triangulations, but when we have two samples of the same fingerprint, we have found more than ten Delaunay Triangulations on average.

An image proof that describes how Delaunay Triangulations act as an effective filter for fingerprint images can be seen in the following 2 scenarios, represented with different graphs.

The first scenario shows two samples from the same fingerprint, whereby a change in pressure levels and a small rotation were registered. A group of images with the Delaunay Triangulations was processed. The results are presented in Fig. 8.

In Fig. 8, we can see that Delaunay Triangulations differ from one another but also that there are specific areas in the Triangulations that contain some triangles with the same characteristics in both image c) and e). In image d) some of the vertices that appear in both triangulations are marked in a softer color. This proves that Delaunay Triangulations can characterize fingerprints even if they differ because of displacement, distorsion, rotations, changes of pressure or other types of alterations.

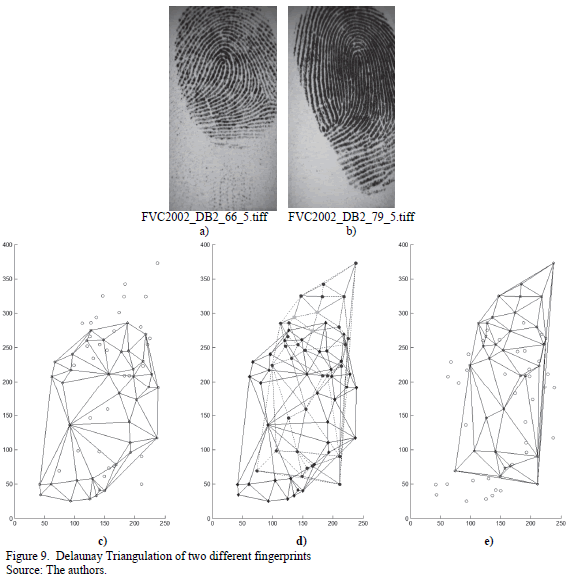
The second scenario shows two samples of two different fingerprints. Because of this, it is expected that no triangle in both Delaunay Triangulations calculated would be classified as equal. This is the most difficult task, because small triangles tend to be very similar in dimensions and angles with respect to others. Fig. 9 shows this.

From the images in Fig. 9 it can be seen that the calculated Delaunay Triangulations are totally different. Because of this, only one triangle is common between both triangulations. It is not easy to find the small triangle marked in a softer color in image d). in the other two images. But it is clear that the triangle marked as equal is very small and easy to classify wrongly.

It is very important to point out that for the experiments shown above, the different geometric thresholds to filter all the triangles in the Delaunay Triangulations had already been taken into account. Otherwise, if only a check up of the triangles present were carried out, almost none of the triangles would be equal to any other in the second triangulation. That can be seen easily in the images.

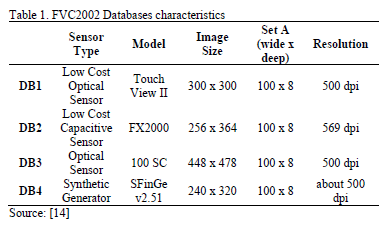
After testing the advantages of using our proposed scheme with some real fingerprint images and effectively characterize their minutiae, we amplified the number of tests in order to get the FAR and FRR thresholds to compare our scheme with other proposals. To obtain such thresholds, we considered 4 fingerprint databases from FVC2002 set A, which are summarized in Table 1.

The threshold depending fraction of the falsely accepted patterns divided by the number of all impostor patterns is called False Acceptance Rate (FAR). Its value is one, if all impostor patterns are falsely accepted and zero, if none of the impostor patterns are accepted. The fraction of the number of rejected client patterns divided by the total number of client patterns is called False Rejection Rate (FRR).

Note that if the score distributions overlap, the FAR and FRR intersect at a certain point. The value of the FAR and the FRR at this point, which is of course the same for both of them, is called the Equal Error Rate (EER).

The EER of a system can be used to give a threshold independent performance measure. The lower the EER, the better the system's performance, as the total error rate which is the sum of the FAR and the FRR at the point of the EER decreases [15].

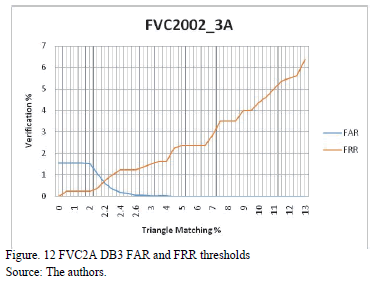
For each fingerprint, 6 random images out of 8 were taken for training, and the remaining 2 were used for verification test purposes. This means that in each database, there were 600 training images and 200 test images. The selection was repeated 4 times with different test images each time. Then, FAR and FRR thresholds for each database were plotted in an image of "verification percentage vs. triangle matching percentage." Figs. 10 to 13 show each of these images.

6. Results

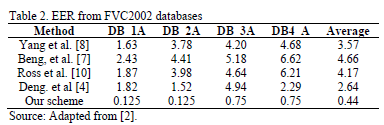
After analyzing the images presented, the ERR was calculated and compared to another 3 proposed schemes. Table 2 shows the summary of the comparison.

As can be seen, the performance of the proposed method exceeds that of those presented in the related work of this article. The difference between the average percentages is about 7 times smaller in our proposal. The main reasons for this happening are related to the type of post processing stage in which our scheme takes place.

Instead of having a dispersion of points in an Cartesian plane, the analysis of minutiae takes place over a polygonal network that minimizes distortion and displacement of the vertices that compose them after image preprocessing and enhancement have been carried out. Also, the criteria established to decide whether a minutia in a fingerprint corresponds to another minutiae in a second fingerprint, strongly depends on a second set of measures from that polygonal network.

Other variables that play an important role in the identity verification results are the geometric thresholds, used to calibrate the training in the verification process. Depending on how strict the verification is required to be and the fingerprint images characteristics (size and resolution), the thresholds can be reduced to allow minimum or maximum variation among the polygonal networks. For the tests presented in this paper, a tolerance of 10 pixels in distance and 10 grades in angles were established.

If there were no alterations because of noise in the media and if the fingerprints do not suffer from erosion or aging, then they must remain equal. But because this is not possible, those thresholds were established based on the premise that different acquisitions from the same fingerprint even on a noisy media have the same degree of alteration in each of its minutiae such as the same degree of rotation, displacement, among others.

7. Conclusions

In this paper, a minutiae based fingerprint verification method was proposed. The innovation of this method relies on the use of Delaunay Triangulations and geometric thresholds to align fingerprint minutiae even in the presence of noise in the environment. Measures of distance, angles of orientation and angles of rotation make it possible to characterize geometric figures with its vertices composed of minutiae avoiding processes of minutiae alignment and matching score calculations. In this way, rotation and displacement tolerance is achieved within the verification process.

It is important to emphasize that a calibration of geometric thresholds must be carried out depending on the characteristics of the fingerprint images, such as size, resolution, etc. With all these conditions achieved, a better EER can be obtained in the tests realized.

Finally, the numerical values and graphs obtained in the tests, confirm that using Delaunay triangulation allows a strict discrimination of minutiae in a fingerprint. However, because the fingerprint images obtained always changes due to pressure, angle and the tilt on capture device, we need to store multiple biometric samples with different conditions to improve the scores. For example, for this paper, 6 images were necessary for each fingerprint..

Acknowledgements

This paper was supported by the CONACyT and the IPN.

References

[1] Wencheng, Y., Jiankun, H. and Wang, S., A delaunay triangle-based fuzzy extractor for fingerprint authentication, Trust, Security and Privacy in Computing and Communications (TrustCom), 2012 IEEE 11^th International Conference on, 66(70), pp. 25-27, 2012. DOI: 10.1109/TrustCom.2012.23

[2] Khalil, M., Mohamad, D., Khurram, K. and Al-Nuzaili, Q., Fingerprint verification using statistical descriptors, Digital Signal Processing 20. ElSevier.Inc. pp.1264-1273, 2009. DOI: 10.1016/j.dsp.2009.12.002

[3] Vianney, J., Rosales, A., Gallegos, F. and Arellano, A., Computer-aided diagnosis of brain tumors using image enhancement and fuzzy logic, DYNA, 81(183), pp 148-157, 2014. DOI: 10.15446/dyna.v81n183.36838

[4] Deng, H. and Huo, Q., Minutiae matching based fingerprint verification using delaunay triangulation and aligned-edge-guided triangle matching. Audio and Video Based Biometric Person Authentication. AVBPA, pp. 270-278, 2005. DOI: 10.1007/11527923_28

[5] Liu, N., Yin, Y. and Zhang, H., A fingerprint matching algorithm based on delaunay triangulation net, Proceedings, International Conference on Computer and Information Technology, CIT05. pp. 591, 595, 2005. DOI: 10.1109/CIT.2005.9

[6] Parziale, G. and Niel, A., A fingerprint matching using minutiae triangulation. ICBA2004, LNCS3072, Springer-Verlag Berlin Heidelberg. pp.241-248, 2004. DOI: 10.1007/978-3-540-25948-0_34

[7] Beng, J., Chek-Ling, D. and Song, O., An efficient fingerprint verification system using integrated wavelet and Fourier-Melling invariant transform, Image and Vision Computing. ElSevier, 22, pp. 503-513, 2003. DOI: 10.1016/j.imavis.2003.12.002

[8] Yang, J. and Park D., A fingerprint verification algorithm using tessellated invariant moment features, Neurocomputing. ElSevier, 7, pp. 1264-1273, 2008. DOI: 10.1016/j.neucom.2007.12.034

[9] Imamverdiyev, Y., Beng, A. and Kim, J., Biometric cryptosystem based on discretized fingerprint texture descriptors, Expert Systems with Applications. 40, pp. 1888-1901, 2012. DOI: 10.1016/j.eswa.2012.10.009

[10] Ross, A., Jain, A. and Reisman, J., A hybrid fingerprint matcher, Pattern Recognition. The Journal of the Pattern Recognition Society. 36, pp. 1661-1673, 2003. DOI: 10.1016/S0031-3203(02)00349-7

[11] Abraham, J., Kwan, P. and Gao, J.. Fingerprint matching using a hybrid shape and orientation descriptor, In: Yang J. (Ed.), State of the art in Biometrics INTECH, ISBN: 978-953-307-489-4, 2011, pp. 25-56, DOI: 10.5772/19105

[12] Berg, M., Cheong, O., van Kreveld, M. and Overmars, M., Computational geometry. Algorithms and applications, Berlin: Springer, 2008. DOI: 10.1007/978-3-540-77974-2

[13] Arens, C., The Bowyer-Watson algorithm. An efficient implementation in a database environment, Thesis, Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, Holand, 2002, pp 5-9.

[14] Cappelli, R., Maio, D., Maltoni, D., Wayman, J.L. and Jain, A.K., Performance evaluation of fingerprint verification systems, IEEE Trans. Pattern Analysis and Machine Intelligence. 28(1), pp. 3-18, 2006. DOI: 10.1109/TPAMI.2006.20

[15] Technical Document About FAR, FRR and EER, Version 1.0, SYRIS Rechnology Corp., 2004, pp 1-4.

M. Ramírez-Flores, received the BSc. in Engineer in Telecommunications and Electronic Systems in 2010, with honorific mention from the Instituto Tecnológico y de Estudios Superiores de Monterrey, Campus Ciudad de México, Mexico. His areas of knowledge are: electronic voting process, secure cryptoimage applications and biometry. ORCID: 0000-0001-5085-9604

G. Aguilar-Torres, has a PhD. in Communications and Electronics. His areas of knowledge are: signal processing, pattern recognition, neural networks and biometry. ORCID: 0000-0002-1808-3962

G.Gallegos-García, has a PhD. in Communications and Electronics. Her areas of knowledge are: e-voting, design of secure cryptoimage applications, information systems and cryptography. ORCID: 0000-0002-5212-350X